（六）树和二叉树

二叉树

　　定义：二叉树是一种树型结构，它的特点是每个结点至多只有两棵子树，并且，二叉树的子树有左右之分，次序不能任意颠倒

　　性质：
　　　①在二叉树的第i层上至多有2^(i-1 )个结点（i≥1）
　　　②深度为k的二叉树至多有2^k-1个结点
　　　③对任何一棵二叉树T，如果其终端结点数为n0，度为2的结点数为n0=n2+1
　　　④具有n个结点的完全二叉树的深度为floor(log2 n)+1

　　二叉树的存储结构
　　　1.顺序存储结构
　　　

1
2
3
　　　#define MAX_TREE_SIZE 100  //二叉树的最大结点数
　　　typedef TElemType SqBiTree[MAX_TREE_SIZE];  //0号单元存储根结点
　　　SqBiTree bt；

　　　将完全二叉树上的编号为i的结点元素存储在如上定义的一位数组中下标为i-1的分量中。
　　　最坏的情况下，一个深度为k且只有k个结点的单支树（树中不存在度为2的结点）却需要长度为2^k-1的一位数组
　　　仅适合用于完全二叉树

　　　2.链式存储结构
　　　

1
2
3
4
　　　typedef struct BiTNode{
    　　TElemType  data;
　　　　struct BiTNode  *lchild, *rchild;  //左右孩子指针
　　　}BiTNode,*BiTree;

　　　遍历二叉树
　　　　1.先序遍历
　　　　
1
2
3
4
5
6
7
8
9
10
　　　　Status Bitree::PreOrderTraverse(const BiTree &T) {
　　　　//先序遍历二叉树T，对每个结点调用函数PrintElement一次且仅一次
　　　　//一旦PrintElement失败，则操作失败
　　　　　if (T) {
　　　　　　PrintElement(T->data);
　　　　　　PreOrderTraverse(T->lchild);
　　　　　　PreOrderTraverse(T->rchild);
　　　　　}
　　　　　return OK;
　　　　}

　　　　
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
　　　　Status PreOrderStack(const BiTree T){
   statck<BiTree> s;
   BiTree p=T;
   while(p||!s.empty()){
     if(p){
       PrintElement(p->data);
       if(p->rchild){
         s.push(p->rchild);
       }
       p=p->lchild;
     }else{
       p=s.top();
       s.pop();
     }
   }
}

　　　　2.中序遍历
　　　　
1
2
3
4
5
6
7
8
9
10
　　　　Status Bitree::InOrderTraverse(const BiTree &T) {
　　　　//中序遍历二叉树T，对每个结点调用函数PrintElement一次且仅一次
　　　　//一旦PrintElement失败，则操作失败
　　　　　if (T) {
　　　　　　InOrderTraverse(T->lchild);
　　　　　　PrintElement(T->data);
　　　　　　InOrderTraverse(T->rchild);
　　　　　}
　　　　　return OK;
　　　　}

　　　　
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
　　　　Status InOrderStack(const BiTree &T) {
  　　　　stack<BiTree> s;
BiTree p=T;
while(p||s.empty()){
  if(p){
    s.push(p);
    p=p->lchild;
  }else{
    p=s.top();
    PrintElement(p->data);
    p=p->rchild;
    s.pop();
  }
}
　　　　　return OK;
　　　　}

　　　　3.后序遍历
　　　　
1
2
3
4
5
6
7
8
9
10
　　　　Status Bitree::PostOrderTraverse(const BiTree &T) {
　　　　//后序遍历二叉树T，对每个结点调用函数PrintElement一次且仅一次
　　　　//一旦PrintElement失败，则操作失败
　　　　　if (T) {
　　　　　　PostOrderTraverse(T->lchild);
　　　　　　PostOrderTraverse(T->rchild);
　　　　　　PrintElement(T->data);
　　　　　}
　　　　　return OK;
　　　　}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Status PostOrderStack(BiTree T){
  Stack s;
  BiTree pre=NULL; //前一个已访问的节点
  InitStack(s);
  if(!T) return OK;
  Push(s,T);
  while(!StackEmpty(s)){
    BiTree cur;
     GetTop(s,cur);
      if((cur->lchild=NULL&&cur->rchild==Null)||(pre!=NULL&&(cur->lchild==pre||cur->rchild==pre))){
         visit(cur);
         pre=cur;
         Pop(s,cur);
      }else{
           if(cur->rchild){
             Push(s,cur->rchild);
           }
         if(cur->lchild){
           Push(s,cur->lchild);
          }

          }
     }
     return OK;
 }

　　　　4.层序遍历
　　　　
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
　　　　Status Bitree::LevelOrderTraverse(const BiTree &T) {
　　　　//层序遍历二叉树T，对每个结点调用函数PrintElement一次且仅一次
　　　　//一旦PrintElement失败，则操作失败
　　　　　queue<BiTree> q;
　　　　　if(T){
　　　　　　q.push(T);
　　　　　　while (!q.empty()) {
　　　　　　　BiTree s=q.front();
　　　　　　　PrintElement(s->data);
　　　　　　　if (s->lchild != NULL) q.push(s->lchild);
　　　　　　　if (s->rchild != NULL) q.push(s->rchild);
　　　　　　　q.pop();
　　　　　　}
　　　　　}
　　　　　return OK;
　　　　}

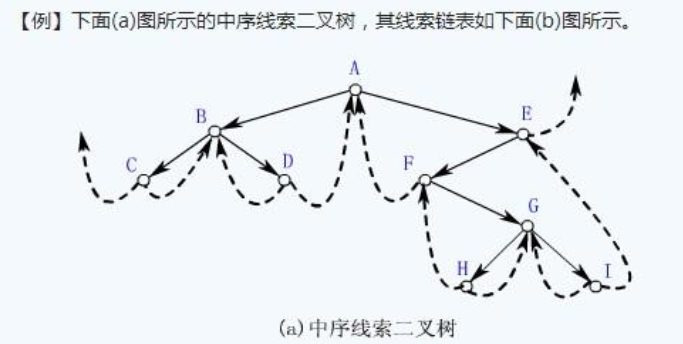
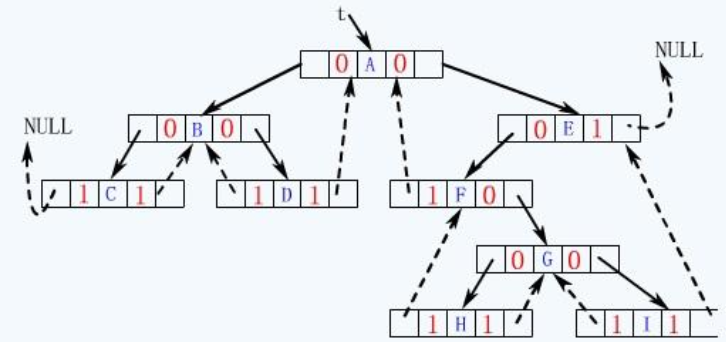
　　　　线索二叉树
　　　　　利用n个结点的二叉树必有n+1个空链域存放指向某种遍历次序下的前驱结点或后继结点的指针

　　　　图示
　　　　　线索二叉树图示
　　　　　线索二叉树图示

　　　　数据结构
　　　　

1
2
3
4
5
6
　　　　typedef enum PointTag{Link,Thread};  //Link==0;指针，Thread==1；线索
　　　　typedef struct BiThrNode{
　　　　　　TElemType  data;
　　　　　　struct BiThrNode  *lchild,*rchild;  //左右孩子指针
　　　　　　PointerTag  LTag,RTag;  //左右标志
　　　　}BiThrNode,*BiThrTree;

树和森林

　　相关术语
　　　树的结点：包含一个数据元素及若干指向其子树的分支
　　　度：结点拥有的子树数称为结点的度(Degree)
　　　叶子：度为0的结点
　　　分支结点：度不为0的结点

　　结点的层次
　　　从根开始定义起，根为第一层，根的孩子为第二层
　　　深度(Depth):树中结点的最大层次
　　　有序树：结点各子树看成从左至右是有次序的（即不能交换的）
　　　*无序树：结点各子树看成从左至右是无次序的（即可以交换的）
　　　*森林(Forest):m(m≥0)棵互不相交的树的集合

　　存储结构
　　　1.双亲表存储表示
　　　

1
2
3
4
5
6
7
8
9
　　　#define MAX_TREE_SIZE 100
　　　typedef struct PTNode{
　　　　　TElemType  data;
　　　　　int  parent;   //双亲位置域
　　　}PTNode;
　　　typedef struct{
　　　　　PTNode nodes[MAXX_TREE_SIZE];
　　　　　int r,n;   //根的位置和结点数
　　　}PTree;

　　　利用每个结点（除根节点外）只有唯一双亲的性质求结点的孩子时需要遍历整个结构

　　　2.孩子链表存储表示
　　　

1
2
3
4
5
6
7
8
9
10
11
12
　　　typedef struct CTNode{
　　　　　int child;
　　　　　struct CTNode *next;
　　　}*ChildPtr;
　　　typedef struct{
　　　　　TElemType  data;
　　　　　ChildPtr  firstchild;  //孩子链表头指针
　　　}CTBox;
　　　typedef struct{
　　　　　CTBox nodes[MAX_TREE_SIZE];
　　　　　int  n,r;  //结点数和根的位置
　　　}CTree;

　　　便于一些涉及孩子的操作，不适用于找双亲

　　　3.二叉链表（孩子-兄弟）存储表示）：
　　　

1
2
3
4
　　　typedef structCSNode{
　　　　　ElemType  data;
　　　　　struct CSNode  *firstchild,*nextsibling;
　　　}CSNode,*CStree;

　　　便于实现各种树的操作

　　森林与二叉树的转换

　　　1.树变二叉树
　　　　兄弟相连，保留长子的连线

　　　2.二叉树变树
　　　　结点的右孩子与其双亲连

　　　3.森林变二叉树
　　　　树变而二叉树，各个树的根相连

哈夫曼树

　　　路径长度
　　　　路径上的分支数目

　　　树的路径长度
　　　　从树根到每个结点的路径长度之和

　　　树的带权路径长度
　　　　所有叶子结点的带权路径长度之和
　　　　WPL=∑（k=1,n）wk*lk
　　　WPL最小的二叉树称作最优二叉树或哈夫曼树

　　　构造
　　　　权值越大，应分配的路径长度越小
　　　　故：
　　　　　将所有带权结点加入集合，每次从结合中选取权值最小的两个结点，生成一个权值为两者权值之和的父节点，父节点加入集合，两个子节点移出集合，重复操作，直至集合只剩下一个结点，即根结点。

　　　应用
　　　　前缀编码

　　　数据结构
　　　

1
2
3
4
5
　　　typedef struct{
　　　　　unsigned int  weight;
　　　　　unsigned int  parent,lchild,rchild;
　　　}HTNode,*HuffmanTree;   //动态分配数组存储哈夫曼树
　　　typedef char **HuffmanCode;  //动态分配数组存储哈夫曼编码表

二叉树代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW_ -2

typedef int Status;
typedef char TElemType;

typedef struct BiTNode {
	TElemType data;
	struct BiTNode * lchild, * rchild;
}BiTNode, * BiTree;

class Bitree {
public:
	Status CreateBiTree(BiTree &T);
	//按先序次序输入二叉树中结点的值（一个字符）,空字符表示空树
	//构造二叉链表表示的二叉树T
	Status PreOrderTraverse(const BiTree &T);
	//先序遍历二叉树T，对每个结点调用函数PrintElement一次且仅一次
	Status InOrderTraverse(const BiTree &T);
	//中序遍历二叉树T，对每个结点调用函数PrintElement一次且仅一次
	//一旦PrintElement失败，则操作失败
	Status PostOrderTraverse(const BiTree &T);
	//后序遍历二叉树T，对每个结点调用函数PrintElement一次且仅一次
	//一旦PrintElement失败，则操作失败
	Status LevelOrderTraverse(const BiTree &T);
	//层序遍历二叉树T，对每个结点调用函数PrintElement一次且仅一次
	//一旦PrintElement失败，则操作失败
	Status DestroyTree(BiTree &T);
	//采用后续遍历销毁二叉树

	Status PrintElement(const TElemType &e) {
		//打印
		cout << e;
		return OK;
	}

	//--------树的应用-------
	Status SearchNode(const BiTree &T,const TElemType &value);
	//查找值为value的结点
	int Leaf(const BiTree &T);
	//求树的叶子数
	int SumNode(const BiTree &T);
	//求结点数
	int Depth(const BiTree &T);
	//求树的高度
	Status PathLeaf(const BiTree &T, stack<BiTree> &S);
	//求所有叶子结点的路径
	Status ExchangeChild(BiTree &T);
	//实现二叉树所有左右子女的互换
	Status MaxPath_PreOrderTraverse(const BiTree &T);
	//采用先序递归遍历算法，求返回第一个最长路径的长度，并输出路径上各节点的值

	Status PrintStack(const stack<BiTree> &S) {
		//遍历栈
		stack<BiTree> x;
		x = S;
		while (!x.empty()) {
			cout << x.top()->data;
			x.pop();
		}
		cout << endl;
		return OK;
	}

};

Status Bitree::CreateBiTree(BiTree &T) {
	//按先序次序输入二叉树中结点的值（一个字符）,空字符表示空树
	//构造二叉链表表示的二叉树T
	char ch;
	cin >> ch;
	if (ch == '#') T = NULL;
	else {
		if (!(T = new BiTNode)) exit(OVERFLOW_);
		T->data = ch;		//生成根结点
		CreateBiTree(T->lchild);  //构造左子树
		CreateBiTree(T->rchild);  //构造右子树
	}
	return OK;
}

Status Bitree::PreOrderTraverse(const BiTree &T) {
	//先序遍历二叉树T，对每个结点调用函数PrintElement一次且仅一次
	//一旦PrintElement失败，则操作失败
	if (T) {
		PrintElement(T->data);
		PreOrderTraverse(T->lchild);
		PreOrderTraverse(T->rchild);
	}
	return OK;
}

Status Bitree::InOrderTraverse(const BiTree &T) {
	//中序遍历二叉树T，对每个结点调用函数PrintElement一次且仅一次
	//一旦PrintElement失败，则操作失败
	if (T) {
		InOrderTraverse(T->lchild);
		PrintElement(T->data);
		InOrderTraverse(T->rchild);
	}
	return OK;
}

Status Bitree::PostOrderTraverse(const BiTree &T) {
	//后序遍历二叉树T，对每个结点调用函数PrintElement一次且仅一次
	//一旦PrintElement失败，则操作失败
	if (T) {
		PostOrderTraverse(T->lchild);
		PostOrderTraverse(T->rchild);
		PrintElement(T->data);
	}
	return OK;
}

Status Bitree::LevelOrderTraverse(const BiTree &T) {
	//层序遍历二叉树T，对每个结点调用函数PrintElement一次且仅一次
	//一旦PrintElement失败，则操作失败
	/* vector<BiTree> Parents;
	vector<BiTree> Children;
	vector<BiTree> AllNode;
	Parents.push_back(T); //根结点入向量
	AllNode.push_back(T); //根结点入总结点向量
	do {
		Children.swap(vector<BiTree>());//暂时清空
		for (unsigned i = 0; i < Parents.size(); i++) {
			if (Parents[i]->lchild) {
				AllNode.push_back(Parents[i]->lchild);
				Children.push_back(Parents[i]->lchild);
			}

			if (Parents[i]->rchild) {
				AllNode.push_back(Parents[i]->rchild);
				Children.push_back(Parents[i]->rchild);
			}
		}
		Parents.swap(vector<BiTree>()); //暂时清空
		for (unsigned i = 0; i < Children.size(); i++) {
			Parents.push_back(Children[i]);
		}
	} while (Parents.size() != 0);
	for (unsigned i = 0; i < AllNode.size(); i++) {
		PrintElement(AllNode[i]->data);
	} */

	queue<BiTree> q;
	if(T){
		q.push(T);
		while (!q.empty()) {
			BiTree s=q.front();
			PrintElement(s->data);
			if (s->lchild != NULL) q.push(s->lchild);
			if (s->rchild != NULL) q.push(s->rchild);
			q.pop();
		}
	}

	return OK;
}

Status Bitree::DestroyTree(BiTree &T) {
	//销毁二叉树
	if (T) { //后序遍历销毁
		DestroyTree(T->lchild);
		DestroyTree(T->rchild);
		delete T;
	}
	T = NULL; //空树标志，仅用于判断空树
	return OK;
}

Status Bitree::SearchNode(const BiTree &T,const TElemType &value) {
	//查找值为value的结点
	if (T) {
		if (T->data == value) {
			cout << "存在值为value的结点" << endl;
			return OK;
		}
		else {
			if (!SearchNode(T->lchild, value)) { //避免树中存在重复值，即在左子树找到值时则不必进入右子树继续查找
				SearchNode(T->rchild, value);
			}
			else
				return OK;
		}
	}
	else
		return ERROR; //查询无果！
}

int Bitree::Leaf(const BiTree &T) {
	//求树的叶子数
	if (!T)  //当前结点不存在，则叶子数为0
		return 0;
	else if (T->lchild == NULL&&T->rchild == NULL) //当前结点的左右孩子为空时，此结点为叶子，叶子数增1
		return 1;
	else
		return Leaf(T->lchild) + Leaf(T->rchild);
	//对于每个结点都采用先判断是否存在，而后是否左右孩子为空，最后对于上述两种情况不存在时，进行两个子树的叶子数求和，以此类推
}

int Bitree::SumNode(const BiTree &T) {
	//求结点数
	if (!T)
		return 0;
	else {
		return SumNode(T->lchild) + SumNode(T->rchild) + 1; //左右子树结点数求和并上自身结点
	}
}

int Bitree::Depth(const BiTree &T) {
	//求树的高度
	if (!T)
		return 0;
	else
		return (Depth(T->lchild) > Depth(T->rchild) ? Depth(T->lchild) : Depth(T->rchild)) + 1; //高度为根结点自身加上两子树高度最大值
}

/*
typedef struct BiTree {
	TElemType data;
	struct BiTree * lchild, * rchild;
}BiTree, * BiTree;

Ctrl+K+D
int Length = -1;
int MaxLength = 0;
Stack S;
Stack Max;
InitStack(S);
InitStack(Max);
Status MaxPath_PreOrderTraverse(BiTree &T，int Length) {
	//采用先序递归遍历算法，求返回第一个最长路径的长度，并输出路径上各节点的值
	if (T) {
		PushBack(S, T);
		Length++;
		MaxPath_PreOrderTraverse(T->lchild, Length);//访问左孩子
		MaxPath_PreOrderTraverse(T->rchild, Length);//访问右孩子
		if ((!T->lchild) && (!T->rchild)) { //叶子节点
			if (Length > MaxLength) {
				MaxLength = Length;
				ClearStack(Max);
				CopyStack(Max, S);
			}
		}

	}
	Length--;//长度退回父节点
	PopStack(S);//节点退回至父节点
	return OK;
}
Status TraverseStack(Stack Max) {
	//逆向遍历栈
	for (p = Max.base; p != Max.top - 1; p++)
		cout << p->data;
	return OK;
}
*/

Status MaxPath_PreOrderTraverse(const BiTree &T,stack<BiTree> &S);
	//采用先序递归遍历算法，求返回第一个最长路径的长度，并输出路径上各节点的值
Status Bitree::PathLeaf(const BiTree &T, stack<BiTree> &S) {
	//求所有叶子结点的路径
	S.push(T);
	if (T) {
		if (T->lchild == NULL&&T->rchild == NULL) {
			PrintStack(S);
		}
		else {
			PathLeaf(T->lchild, S);
			S.pop();  
			PathLeaf(T->rchild, S);
			S.pop();
		}
	}
	return OK;
}

/* 上述代码等同于下列代码
    //分析如下：
	//两者最大的不同为上述为引用参数,而下述代码为非引用参数，传递时仅是备份传入，
	//即把根结点的左或右孩子入栈进行相应操作后，返回当前根结点时，栈仍然为仅将根结点入栈的状况，故不用考虑出栈
Status Bitree::PathLeaf(const BiTree &T, stack<BiTree> S) {
	//求所有叶子结点的路径
	S.push(T);
	if (T) {
		if (T->lchild == NULL&&T->rchild == NULL) {
			PrintStack(S);
		}
		else {
			PathLeaf(T->lchild, S);
			PathLeaf(T->rchild, S);
		}
	}
	return OK;
}
*/
Status Bitree::ExchangeChild(BiTree &T){
	//实现二叉树所有左右子女的互换
	BiTree temp;
	if(T){
		temp=T->lchild;
		T->lchild=T->rchild;
		T->rchild=temp;
		ExchangeChild(T->lchild);
		ExchangeChild(T->rchild);
	}
	return OK;
}

哈夫曼树代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW_ -2
typedef int Status;
typedef char TElemType;
using namespace std;
typedef struct{
	unsigned int weight;
	unsigned int parent,lchild,rchild;
}HTNode,*HuffmanTree;
typedef char * * HuffmanCode;

bool cmp(HuffmanTree a, HuffmanTree b){
	return a->weight<b->weight;
}

Status Init(unsigned int *w,int n) {
	for (int i = 0; i < n; i++) {
		cin >> w[i];
	}
	return OK;
}

Status Select(HuffmanTree HT,int number,int &s1,int &s2){
	//在HT[1..number]选择parent为0且weight最小的两个结点，其序号分别为s1和s2
	//HuffmanTree p=HT;
	//sort(p+1,p+number+1,cmp);//按权值升序排列
	for (int i = 1; i <= number; i++) {
		if (HT[i].parent == 0) {
			s1 = i;
			break;
		}
	}
	for (int i = 1; i <= number; i++) {
		if (HT[i].parent == 0 && HT[i].weight < HT[s1].weight)
			s1 = i;
	}
	for (int i = 1; i <= number; i++) {
		if (HT[i].parent == 0&&i!=s1){
			s2 = i;
			break;
		}
	}
	for (int i = 1; i <= number; i++) {
		if (HT[i].parent == 0 && i!=s1&&HT[i].weight < HT[s2].weight)
			s2 = i;
	}
	return OK;
}

Status HuffmanCoding(HuffmanTree &HT,HuffmanCode &HC,unsigned int *w,unsigned int n){
	//w存放n个字符的权值（均>0），构造哈弗曼树HT，并求出n个字符的哈弗曼编码HC
	if(n<=1) return ERROR;
	unsigned int m=2*n-1;
	HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode));
	unsigned int i;
	HuffmanTree p;
	for(p=HT+1,i=1;i<=n;++i,++p,++w) *p={*w,0,0,0};
	for (; i <= m; ++i, ++p) *p = { 0,0,0,0 };
	for(i=n+1;i<=m;i++){ //创建哈弗曼树
		//在HT[1...i-1]选择parent为0且weight最小的两个结点，其序号分别为s1和s2.
		int s1,s2;
		Select(HT,i-1,s1,s2);
		HT[s1].parent=i;HT[s2].parent=i;
		HT[i].lchild=s1;HT[i].rchild=s2;
		HT[i].weight=HT[s1].weight+HT[s2].weight;
	}
	//---从叶子到根逆向求每个字符的哈弗曼编码---
	HC=(HuffmanCode)malloc((n+1)*sizeof(char*)); //分配n个字符编码的头指针向量
	char *cd=(char*)malloc(n*sizeof(char));//分配求编码的工作空间
	cd[n-1]='\0';
	for(i=1;i<=n;++i){ //逐个字符求哈弗曼编码
		unsigned int start=n-1;
		for(unsigned int c=i,f=HT[i].parent;f!=0;c=f,f=HT[f].parent) //从叶子到根逆向求编码
			if(HT[f].lchild==c) cd[--start]='0';
			else cd[--start]='1';
		HC[i]=(char*)malloc((n-start)*sizeof(char));//为第i个字符编码分配空间
		//strcpy(HC[i], &cd[start]);
		strcpy_s(HC[i],n-start,&cd[start]);
	}

	free(cd);   //释放工作空间
	return OK;
}
赏

Thank you for inviting me to have candy.

支付宝
微信

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置：

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

做一个安静细微的人，<br> 于角落里自在开放，<br> 默默悦人，<br> 却始终不引起过分热闹的关注，<br> 保有独立而随意的品格，<br> 这就很好。<br><br> Stick to what you insist on,<br> believe what you believe!<br> Life hastily for decades,<br> do what I can!