（七）图

2017-06-20

相关定义和术语

　　图的逻辑结构特征就是其结点（顶点）的前驱和后继的个数都是没有限制的，即任意两个节点之间都可能相关

图Graph

　　G=（V，E）
　　V是顶点的有穷非空集合，E是顶点偶对的有穷集

　　有向图（Digraph）：每条边都有方向；
　　*无向图（Undigraph）：每条边没有方向；
　　有向完全图：具有n(n-1)条边的有向图；
　　无向完全图*：具有n(n-1)/2跳变的无向图
　　网络：带权图

　　连通图（待跟进）：
　　　1.无向图G中，从v到v’有路径，两者连通任意两顶点都联通，则G是连通图非连通图中，存在的连通分量指无向图中的极大连通子图
　　　2.在有向图G中，如果两顶点有路径（注意方向），则连通若每一对顶点之间都联通，则G是强连通图强连通分量指有向图中的极大强连通子图
　　　3.一个连通图的生成树是一个极小连通子图，它包含图中全部顶点，但只有足以构成一棵树的n-1条边

图的存储结构

　　1.邻接矩阵表示法
　　

　　#define INFINITY_ INT_MAX    //最大值∞
　　#define MAX_VERTEX_NUM 20    //最大顶点个数
　　//typedef enum{DG,DN,UDG,UDN} GraphKind;    //有向图，有向网，无向图，无向网
　　typedef int GraphKind;    //有向图，有向网，无向图，无向网 0 1 2 3

　　typedef struct ArcCell {
　　　　VRType adj;        //VRType是顶点关系类型。对无权图，用1或0表示相邻否；对带权图，则为值权类型
　　　　InfoType *info;        //该弧相关信息的指针
　　}ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];

　　typedef struct {
　　    VertexType vexs[MAX_VERTEX_NUM];    //顶点向量
　　　　AdjMatrix arcs;        //邻接矩阵
　　　　int vexnum, arcnum;        //图的当前顶点数和弧数
　　　　GraphKind kind;        //图的种类标志
　　}MGraph;

　　图示：
　　

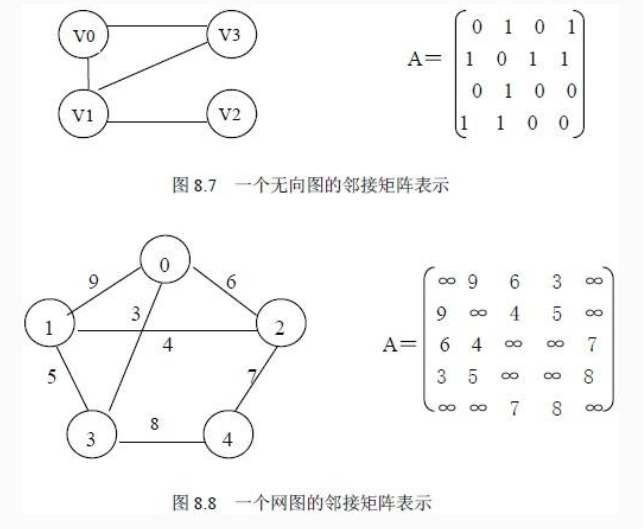
　　2.邻接表表示法
　　

　　#define MAX_VERTEX_NUM 20
　　typedef struct ArcNode {
　　　　int adjvex;                     //该弧所指向的顶点的位置
　　　　struct ArcNode *nextarc;    //指向下一条弧的指针
　　　　InfoType *info;               //该弧相关信息的指针
　　}ArcNode;

　　typedef struct VNode {
　　　　VertexType data;     //顶点信息
　　　　ArcNode *firstarc;    //指向第一条依附该顶点的弧的指针
　　}VNode, AdjList[MAX_VERTEX_NUM];

　　typedef struct {
　　　　AdjList vertices;
　　　　int vexnum, arcnum;    //图的当前顶点数和弧数
　　　　int kind;           //图的种类标志
　　}ALGraph;

　　图示：
　　　

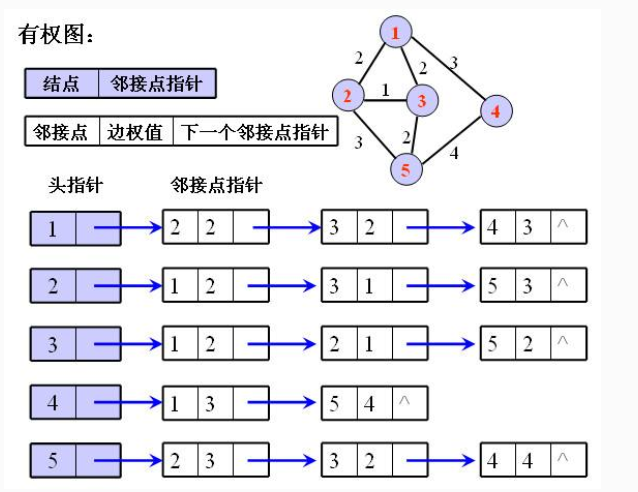
　　3.十字链表表示法
　　

　　#define MAX_VERTEX_NUM 20
　　typedef struct ArcBox{
　　　　int tailvex,headvex;    //该弧的尾和头顶点的位置
　　　　struct ArcBox *hlink,*tlink;    //分别为弧头和弧尾相同的弧的链域
　　　　InfoType *info;    //该弧相关信息的指针
　　}ArcBox;

　　typedef struct VexNode{
　　　　VertexType data;
　　　　ArcBox *firstin,*firstout;    //分别指向该顶点第一条入弧和出弧
　　}VexNode;

　　typedef struct{
　　　　VexNode xlist[MAX_VERTEX_NUM];    //表头向量
　　　　int vexnum,arcnum;    //有向图的当前顶点数和弧数
　　}OLGraph;

　　图示：
　　

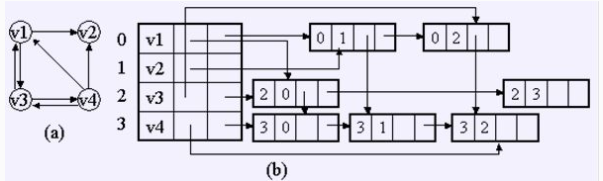
图的遍历

　　1.深度优先搜索Depth_First Search
　　

　　static const int MAX = 1000;
　　bool visited[MAX];
　　Status Algraph::DFSTraverse(ALGraph G) {
　　//深度优先遍历
　　　　for (int v = 0; v < G.vexnum; v++) visited[v] = false;
　　　　for (int v = 0; v < G.vexnum; v++) {  //非连通图或连通图都可遍历
　　　　　　if (!visited[v]) DFS(G, v);
　　　　}
　　　　return OK;
　　}
　　Status Algraph::DFS(ALGraph G, int v) {
　　//从第v个开始遍历
　　　visited[v] = true;
　　　VisitFunc(G, v);
　　　ArcNode* p = G.vertices[v].firstarc;
　　　while (p) {
　　　　if (!visited[p->adjvex])
　　　　　DFS(G, p->adjvex);
　　　　p = p->nextarc;
　　　}
　　　//for (int w = FirstAdjVex(G, v); w ; w = NextAdjVex(G, v, w))
　　　//if (!visited[w]) DFS(G, w);
　　　return OK;
　　}
　　Status Algraph::VisitFunc(ALGraph G, int v) {
　　//访问顶点
　　　　cout << G.vertices[v].data;
　　　　return OK;
　　}

　　图示
　　　

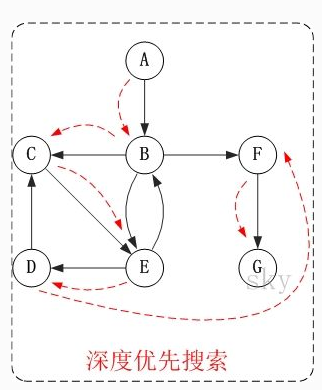
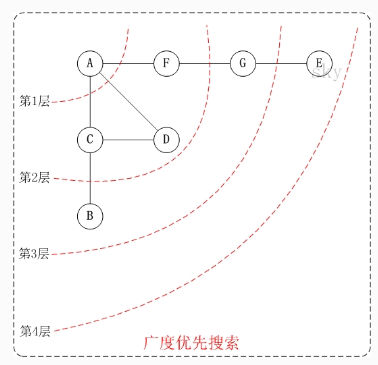
　　2.广度优先搜索Broadth_First Search：
　　

　　Status BFSTraverse(Graph G){
　　//按广度优先非递归遍历
　　　　for(v=0;v<G.vexnum;++v)
　　　　　visited[v]=false;
　　　　queue<int> Q;
　　　　for(v=0;v<G.vexnum;++v){  //非连通图或连通图
　　　　　　if(!visited[v]){
　　　　　　　　visited[v]=true;
　　　　　　　　Visit(v);
　　　　　　　　Q.push(v);
　　　　　　　　while(!Q.empty()){
　　　　　　　　　　int u=Q.front();
　　　　　　　　　　Q.pop();
　　　　　　　　　　for(w=FisrstAdjVex(G,u);w≥0;w=NextAdjVex(G,u,w)){
　　　　　　　　　　　　if(!visited[w]){
　　　　　　　　　　　　　visited[w]=true;
　　　　　　　　　　　　　Visit(w);
　　　　　　　　　　　　　Q.push(w);
　　　　　　　　　　}
　　　　　　　　}
　　　　　　}
　　　　}
　　}

　　图示
　　　　

最小生成树

　　1.Prim算法
　　　先将u0入集合，再从剩下的顶点中找出与该集合中顶点最小边的顶点加入集合，直至所有顶点加入集合为止
　　

　　Status Mgraph::MiniSpanTree_PRIM(MGraph G, VertexType u) {
　　//用普里姆算法 从顶点u出发构造网G的最小生成树T，输出T的各条边
　　struct {
　　　　VertexType adjvex;
　　　　VRType lowcost;
　　}closedge[MAX_VERTEX_NUM];

　　int k = LocateVex(G, u);
　　for (int i = 0; i < G.vexnum; i++)
　　　　if (i != k) closedge[i] = { u,G.arcs[k][i].adj }; //辅助数组初始化
　　closedge[k].lowcost = 0;
　　for (int i = 1; i < G.vexnum; i++) {  //n-1次
　　　　int now = k;
　　　　int min = INT_MAX;
　　　　for (int k = 0; k < G.vexnum; k++) {   //找出最短边的顶点
　　　　　　if (closedge[k].lowcost != 0 && closedge[k].lowcost < min) {  //U内与V-U的最小边的顶点
　　　　　　　　now = k;
　　　　　　　　min = closedge[k].lowcost;
　　　　　　}
　　　　}

　　　　cout << setw(2)<< closedge[now].adjvex << setw(2)<< G.vexs[now] << setw(2)<<min<< endl;

　　　　closedge[now].lowcost = 0;    //第k个顶点入u

　　　　for (int j = 0; j < G.vexnum; j++) {   //更新U与V-U相连的顶点
　　　　　　if (G.arcs[now][j].adj < closedge[j].lowcost)
　　　　　　　　closedge[j] = { G.vexs[now],G.arcs[now][j].adj };
　　　　　　}
　　　}

　　　return OK;

　　}

　　2.Kruskal算法
　　　在E中选择代价最小的边，若该边依附的顶点落在T中不同的连通分量上，则将此边加入到T中，否则舍去此边而选择下一条代价最小的边，直至所有顶点在同一连通分量上
　　

　　Status Mgraph::MiniSpanTree_Kruskal(MGraph G){
　　//标记每个顶点所在的集合
　　　　int mark[MAX_VERTEX_NUM] = { 0 };
　　　　int i = 0, j = 0, k = 0, temp1 = 0, temp2 = 0, sum = 0;
　　　　int min = INFINITY_, fromvex = 0, endvex = 0, t = 0;
　　　　//将所有顶点分属不同集合
　　　　for (i = 0; i <= G.vexnum - 1; i++)
　　　　　mark[i] = i;

　　　　//cout << "Kruskal算法结果：" << endl;
　　　　for (t = 1; t <= G.vexnum - 1; t++) { //最多n-1条边
　　　　　//找到权值最小的那条边，并且首尾顶点不在同一个集合
　　　　　　min = INFINITY_;
　　　　　　for (i = 0; i <= G.vexnum - 1; i++) //找满足算法的最小边
　　　　　　for (j = i + 1; j <= G.vexnum - 1; j++)
　　　　　　　　if (mark[i] != mark[j] && G.arcs[i][j].adj < min) {
　　　　　　　　　　min = G.arcs[i][j].adj;
　　　　　　　　　　fromvex = i;
　　　　　　　　　　endvex = j;
　　　　　　　　　}
　　　　if (min != INFINITY_) { //输出
　　　　　　cout << setw(4) << G.vexs[fromvex]<< setw(2) << G.vexs[endvex] << setw(2) << min << endl;
　　　　　　sum++;
　　　　}
　　　//将首尾顶点所在的两个顶点集合合并为一个集合 机智！！！！！！！！！！
　　　　temp1 = mark[endvex];
　　　　temp2 = mark[fromvex];
　　　　for (k = 0; k <= G.vexnum - 1; k++) {
　　　　　if (mark[k] == temp1)
　　　　　　　mark[k] = temp2;
　　　　}
　　　}
　　　if (sum != G.vexnum - 1)
　　　　　cout << "没有最小生成树" << endl << endl;
　　　return OK;
　　}

拓扑排序

　　　构造拓扑有序序列：
　　　①在有向图中选择一个没有前驱的顶点且输出之
　　　②从图中删除该顶点和所有以它为尾的弧

　　　拓扑序列不唯一

最短路径

　　　1.Dijkstra算法
　　

　　const int MAX = 501;
　　typedef struct {
　　　　int matrix[MAX][MAX]; //初始化
　　　　//int cost[MAX][MAX];
　　　　int vexnum, arcnum;
　　}MyGraph;
　　int main() {
　　　　MyGraph G;
　　　　int c1, c2;
　　　　fill(G.matrix[0], G.matrix[0] + MAX*MAX,INT_MAX);
　　　　cin >> G.vexnum >> G.arcnum >> c1 >> c2;
　　　　for (int i = 0; i < G.arcnum; i++) {
　　　　　　int x, y, len;
　　　　　　cin >> x >> y >> len ;
　　　　　　G.matrix[x][y]= G.matrix[y][x]=len;
　　　　}
　　　　int D[MAX]; //辅助向量
　　　　bool S[MAX]; //S集合
　　　　fill(D, D + MAX, INT_MAX);
　　　　fill(S, S + MAX, false);
　　　　D[c1] = 0;
　　　　S[c1] = true;
　　　　for (int i = 0; i < G.vexnum; i++) {  //初始化D[]
　　　　　　D[i] = G.matrix[c1][i];
　　　　}
　　　　for (int i = 1; i < G.vexnum; i++) {  //主循环
　　　　　　int now=c1;
　　　　　　int mindis=INT_MAX;
　　　　　　for (int i = 0; i < G.vexnum; i++) {    //找与当前now最近的点
　　　　　　　　if (!S[i] && D[i] < mindis) {
　　　　　　　　　　now = i;
　　　　　　　　　　mindis = D[i];
　　　　　　　　}
　　　　　　}
　　　　　　S[now] = true;
　　　　　　for (int i = 0; i < G.vexnum; i++) {    //更新D[]
　　　　　　　　if (!S[i] && G.matrix[now][i] < INT_MAX) { //找到与当前now相连的点
　　　　　　　　　　if (G.matrix[now][i] + D[now] < D[i]) {
　　　　　　　　　　　　D[i] = G.matrix[now][i] + D[now];
　　　　　　　　　　　}
　　　　　　　　　}
　　　　　　}
　　　　}
　　　　cout << D[c2];
　　　　return 0;
　　}

　　2.Floyd-Warshall算法
　　（待跟进）

图代码

#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW_ -2

typedef int Status;
typedef int VRType;
typedef int InfoType;
typedef char VertexType;

//----------------图的数（邻接矩阵）存储表示--------------------
#define INFINITY_ INT_MAX	//最大值∞
#define MAX_VERTEX_NUM 20	//最大顶点个数
//typedef enum{DG,DN,UDG,UDN} GraphKind;	//有向图，有向网，无向图，无向网
typedef int GraphKind;	//有向图，有向网，无向图，无向网 0 1 2 3

typedef struct ArcCell {
	VRType adj;		//VRType是顶点关系类型。对无权图，用1或0表示相邻否；对带权图，则为值权类型
	InfoType * info;		//该弧相关信息的指针
}ArcCell, AdjMatrix[MAX_VERTEX_NUM] [MAX_VERTEX_NUM];

typedef struct {
	VertexType vexs[MAX_VERTEX_NUM];	//顶点向量
	AdjMatrix arcs;		//邻接矩阵
	int vexnum, arcnum;		//图的当前顶点数和弧数
	GraphKind kind;		//图的种类标志
}MGraph;


class Mgraph {
public:
	Status LocateVex(MGraph G, VertexType v);
	//定位v在G中的位置，即在一位数组vexs中的序号
	Status CreateMGraph(MGraph &G);
	//采用数组（邻接矩阵）表示法，构造图G
	Status PrintMGraph(MGraph G);
	//打印无向网G
	Status MiniSpanTree_PRIM(MGraph G, VertexType u);
	//用普里姆算法 从顶点u出发构造网G的最小生成树T，输出T的各条边
	Status Mgraph::MiniSpanTree_Kruskal(MGraph G);
	//用克鲁斯卡尔算法 从顶点u出发构造网G的最小生成树T，输出T的各条边
};


Status Mgraph::LocateVex(MGraph G, VertexType v) {
	//定位v在G中的位置，即在一位数组vexs中的序号
	for (int i = 0; i < G.vexnum; i++) {
		if (G.vexs[i] == v)
			return i;
	}
	return ERROR;	//未找到该顶点
}

Status Mgraph::CreateMGraph(MGraph &G) {
	//采用数组（邻接矩阵）表示法，构造图G
	cin >> G.kind; //图的类型
	//int IncInfo;
	cin >> G.vexnum >> G.arcnum;//>> IncInfo;	//IncInfo为0，则各弧不含其他信息

	for (int i = 0; i < G.vexnum; i++) cin >> G.vexs[i];		//构造顶点向量

	for (int i = 0; i < G.vexnum; i++)		//初始化邻接矩阵
		for (int j = 0; j < G.vexnum; j++)
			G.arcs[i] [j] = { INFINITY_,NULL };

	for (int k = 0; k < G.arcnum; k++) {
		VertexType v1, v2;
		int w;
		cin >> v1 >> v2 >> w;
		if ((G.kind == 0 || G.kind == 2) && (w != 0 && w != 1))
			return ERROR; //有向图与无向图不带权值，w仅有0或1两种状态
		int i = LocateVex(G, v1);
		int j = LocateVex(G, v2);	//确定v1和v2在G中的位置
		G.arcs[i] [j].adj = w;
		//if(IncInfo) Input(* G.arcs[i] [j].info);	//置<v1,v2>的对称弧<v2,v1>
		if (G.kind != 0 && G.kind != 1)
			G.arcs[j] [i] = G.arcs[i] [j];
	}

	return OK;
}

Status Mgraph::PrintMGraph(MGraph G) {
	//打印无向网G
	for (int i = 0; i < G.vexnum; i++)
		for (int j = i; j < G.vexnum; j++) {
			if (G.arcs[i] [j].adj != INT_MAX) {
				if (G.kind == 0)
					cout << G.vexs[i] << "->" << G.vexs[j] << endl; //有向图输出格式
				if (G.kind == 1)
					cout << G.vexs[i] << "-" << G.arcs[i] [j].adj << "->" << G.vexs[j] << endl; //有向网输出格式
				if (G.kind == 2)
					cout << G.vexs[i] << "-" << G.vexs[j] << endl; //无向图输出格式
				if (G.kind == 3)
					cout << G.vexs[i] << "-" << G.arcs[i] [j].adj << "-" << G.vexs[j] << endl; //无向网输出格式
			}

		}
	return OK;
}

Status Mgraph::MiniSpanTree_PRIM(MGraph G, VertexType u) {
	//用普里姆算法 从顶点u出发构造网G的最小生成树T，输出T的各条边
	struct {
		VertexType adjvex;
		VRType lowcost;
	}closedge[MAX_VERTEX_NUM];

	int k = LocateVex(G, u);
	for (int i = 0; i < G.vexnum; i++)
		if (i != k) closedge[i] = { u,G.arcs[k] [i].adj }; //辅助数组初始化
	closedge[k].lowcost = 0;
	for (int i = 1; i < G.vexnum; i++) {  //n-1次
		int now = k;
		int min = INT_MAX;
		for (int k = 0; k < G.vexnum; k++) {   //找出最短边的顶点
			if (closedge[k].lowcost != 0 && closedge[k].lowcost < min) {  //U内与V-U的最小边的顶点
				now = k;
				min = closedge[k].lowcost;
			}
		}

			cout << setw(2)<< closedge[now].adjvex << setw(2)<< G.vexs[now] << setw(2)<<min<< endl;

			closedge[now].lowcost = 0;	//第k个顶点入u

			for (int j = 0; j < G.vexnum; j++) {   //更新U与V-U相连的顶点
				if (G.arcs[now] [j].adj < closedge[j].lowcost)
					closedge[j] = { G.vexs[now],G.arcs[now] [j].adj };
			}
		}

	return OK;
}

Status Mgraph::MiniSpanTree_Kruskal(MGraph G)
{
	//标记每个顶点所在的集合
	int mark[MAX_VERTEX_NUM] = { 0 };
	int i = 0, j = 0, k = 0, temp1 = 0, temp2 = 0, sum = 0;
	int min = INFINITY_, fromvex = 0, endvex = 0, t = 0;
	//将所有顶点分属不同集合
	for (i = 0; i <= G.vexnum - 1; i++)
		mark[i] = i;

    //cout << "Kruskal算法结果：" << endl;
	for (t = 1; t <= G.vexnum - 1; t++) { //最多n-1条边
		//找到权值最小的那条边，并且首尾顶点不在同一个集合
		min = INFINITY_;
		for (i = 0; i <= G.vexnum - 1; i++) //找满足算法的最小边
			for (j = i + 1; j <= G.vexnum - 1; j++)
				if (mark[i] != mark[j] && G.arcs[i][j].adj < min) {
					min = G.arcs[i][j].adj;
					fromvex = i;
					endvex = j;
				}
		if (min != INFINITY_) { //输出
			cout << setw(4) << G.vexs[fromvex]
				<< setw(2) << G.vexs[endvex] << setw(2) << min << endl;
			sum++;
		}
		//将首尾顶点所在的两个顶点集合合并为一个集合 机智！！！！！！！！！！
		temp1 = mark[endvex];
		temp2 = mark[fromvex];
		for (k = 0; k <= G.vexnum - 1; k++) {
			if (mark[k] == temp1)
				mark[k] = temp2;
		}
	}
	if (sum != G.vexnum - 1)
		cout << "没有最小生成树" << endl << endl;
	return OK;
}

//------------------------图的邻接表存储表示-------------------------
#define MAX_VERTEX_NUM 20
typedef struct ArcNode {
	int adjvex;				     //该弧所指向的顶点的位置
	struct ArcNode * nextarc;	//指向下一条弧的指针
	InfoType * info;			   //该弧相关信息的指针
}ArcNode;

typedef struct VNode {
	VertexType data;	 //顶点信息
	ArcNode * firstarc;	//指向第一条依附该顶点的弧的指针
}VNode, AdjList[MAX_VERTEX_NUM];

typedef struct {
	AdjList vertices;
	int vexnum, arcnum;	//图的当前顶点数和弧数
	int kind;		   //图的种类标志
}ALGraph;


Algraph {
private:
	static const int MAX = 1000;
	bool visited[MAX];
public:
	Status CreateAGList(ALGraph &G, int i);
	//创建头链表
	Status CreatALGraph(ALGraph &G);
	//采用邻接表法，构造图G
	Status PrintALGraph(ALGraph G);
	//打印图
	Status LocateALGraphVex(ALGraph G, VertexType v);
	//定位v在G中的位置，即在一位数组vexs中的序号
	Status CreatALGraph_(ALGraph &G);
	//创建
	Status VisitFunc(ALGraph G, int v);
	//访问顶点
	Status DFSTraverse(ALGraph G);
	//深度优先遍历
	Status DFS(ALGraph G, int v);
	//从第v个开始遍历
	Status FirstAdjVex(ALGraph G, int v);
	//返回v的第一个邻接顶点，若没有则返回空
	Status NextAdjVex(ALGraph G, int v, int w);
	//返回v的相对于w的下一个邻接顶点，若w是v的最后一个邻接点，则返回空
};

Status Algraph::CreateAGList(ALGraph &G, int i) {
	//创建头链表
	//ArcNode * p;
	//p = G.vertices[i].firstarc;
	int x;
	cin >> x;
	if (x != -1) {
		ArcNode * q = new ArcNode;
		q->adjvex = x;
		if (G.kind == 1 || G.kind == 3) { //有向网或无向网输入权值
			q->info = new InfoType;
			cin >> * q->info;
		}
		q->nextarc = G.vertices[i].firstarc;
		G.vertices[i].firstarc = q;
		//q->nextarc = p;
		//p = q;
		CreateAGList(G, i);
	}
	return OK;
}

Status Algraph::CreatALGraph(ALGraph &G) {
	//采用邻接表法，构造图G
	cin >> G.kind;	//图的种类
	cin >> G.vexnum >> G.arcnum;	//图的顶点数和弧数
	for (int i = 0; i < G.vexnum; i++) {
		cin >> G.vertices[i].data;	//构造顶点向量

		G.vertices[i].firstarc = NULL;  //头结点初始化

		CreateAGList(G, i);
	}
	return OK;
}

Status Algraph::PrintALGraph(ALGraph G) {
	//打印图
	for (int i = 0; i < G.vexnum; i++) {
		ArcNode * p = G.vertices[i].firstarc;
		while (p) {
			if (G.kind == 0)	//有向图
				cout << G.vertices[i].data << "->" << G.vertices[p->adjvex].data << endl;
			if (G.kind == 1)	//有向网
				cout << G.vertices[i].data << "-" << * p->info << ">" << G.vertices[p->adjvex].data << endl;
			if (G.kind == 2)  //无向图
				cout << G.vertices[i].data << "-" << G.vertices[p->adjvex].data << endl;
			if (G.kind == 3)  //无向网
				cout << G.vertices[i].data << "-" << * p->info << "-" << G.vertices[p->adjvex].data << endl;
			p = p->nextarc;
		}
	}
	return OK;
}

Status Algraph::LocateALGraphVex(ALGraph G, VertexType v) {
	//定位v在G中的位置，即在一位数组vexs中的序号
	for (int i = 0; i < G.vexnum; i++) {
		if (G.vertices[i].data == v)
			return i;
	}
	return ERROR;	//未找到该顶点
}

Status Algraph::CreatALGraph_(ALGraph &G) {
	//创建
	cin >> G.kind;	//图的种类
	cin >> G.vexnum >> G.arcnum;	//图的顶点数和弧数
	for (int i = 0; i < G.vexnum; i++) {
		cin >> G.vertices[i].data;	//构造顶点向量
		G.vertices[i].firstarc = NULL;  //头结点初始化
	}
	for (int i = 0; i < G.arcnum; i++) {
		char v1, v2;
		int w;
		cin >> v1 >> v2;
		if (G.kind == 1 || G.kind == 3)//带权图
			cin >> w;
		int m, n;
		m = LocateALGraphVex(G, v1);
		n = LocateALGraphVex(G, v2);
		ArcNode* p = new ArcNode;
		p->adjvex = n;
		if (G.kind == 1 || G.kind == 3)//带权图
		{
			p->info = new InfoType;
			* p->info = w;
		}
		p->nextarc = G.vertices[m].firstarc;
		G.vertices[m].firstarc = p;
	}
	return 0;
}

Status Algraph::VisitFunc(ALGraph G, int v) {
	//访问顶点
	cout << G.vertices[v].data;
	return OK;
}

Status Algraph::DFSTraverse(ALGraph G) {
	//深度优先遍历
	for (int v = 0; v < G.vexnum; v++) visited[v] = false;
	for (int v = 0; v < G.vexnum; v++) {
		if (!visited[v]) DFS(G, v);
	}
	return OK;
}

Status Algraph::DFS(ALGraph G, int v) {
	//从第v个开始遍历
	visited[v] = true;
	VisitFunc(G, v);
	ArcNode* p = G.vertices[v].firstarc;
	while (p) {
		if (!visited[p->adjvex])
			DFS(G, p->adjvex);
		p = p->nextarc;
	}
	//for (int w = FirstAdjVex(G, v); w ; w = NextAdjVex(G, v, w))
		//if (!visited[w]) DFS(G, w);
	return OK;
}

Status Algraph::FirstAdjVex(ALGraph G, int v) {
	//返回v的第一个邻接顶点，若没有则返回空
	if (G.vertices[v].firstarc)
		return G.vertices[v].firstarc->adjvex;
	else
		return ERROR;
}

//返回v的第一个邻接顶点，若没有则返回空
Status Algraph::NextAdjVex(ALGraph G, int v, int w) {
	//返回v的相对于w的下一个邻接顶点，若w是v的最后一个邻接点，则返回空
	ArcNode* p = G.vertices[v].firstarc;
	for (; p != NULL&&p->adjvex != w; p = p->nextarc);
	if (p != NULL&&p->nextarc != NULL)
		return p->nextarc->adjvex;
	else
		return ERROR;
}



//-------------------有向图的十字链表存储表示--------------
#define MAX_VERTEX_NUM 20
typedef struct ArcBox{
	int tailvex,headvex;	//该弧的尾和头顶点的位置
	struct ArcBox * hlink,* tlink;	//分别为弧头和弧尾相同的弧的链域
	InfoType * info;	//该弧相关信息的指针
}ArcBox;
typedef struct VexNode{
	VertexType data;
	ArcBox * firstin,* firstout;	//分别指向该顶点第一条入弧和出弧
}VexNode;
typedef struct{
	VexNode xlist[MAX_VERTEX_NUM];	//表头向量
	int vexnum,arcnum;	//有向图的当前顶点数和弧数
}OLGraph;

Status CreateDG(OLGraph &G){
	//采用十字链表存储表示，构造有向图G(G.kind=DG)
	cin>>G.vexnum>>G.arcnum>>IncInfo;	//IncInfo为0则各弧不含其他信息
	for(int i=0;i<G.vexnum;i++){

		cin>>G.xlist[i].data;	//输入顶点值
		G.xlist[i].firstin=NULL;
		G.xlist[i].firstout=NULL;	//初始化指针

	}

	for(int k=0;k<G.arcnum;k++){
		cin>>v1>>v2;
		i=LocateVex(G,v1);
		j=LocateVex(G,v2);
		p=(ArcBox*)malloc(sizeof(ArcBox));
		* p={i,j,G.xlist[j].firstin,G.xlist[i].firstout,NULL}

		G.xlist[j].firstin=G.xlist[i].firstout=p;
		if(IncInfo) Input(* p->info);
	}
	return OK;
}

int count = 0;
Status Count_path_BFS(ALGraph G,int i,int j,int k) {
	//采用广度优先计算 i到j长度为k的路径数（含回路）
	int count = 0, number = 0, flag;
	bool visited[G.vexnum];

	fill(visited, visited + G.vexnum, false);

	InitStack(S); //结点栈
	InitStack(Lenth); //各结点距离i的长度栈
	push(S, i)
	push(Lenth, number);
	while (!StackEmpty(S)) {
		pop(S, m)

		pop(Lenth, n);
		if (j == m&&n == k) {
			count++;
		}
		flag = 0
			for (v = 0; v < G.vexnum; v++) {
				if (G.arcs[m] [v] != 0) {
					push(S, v);
					if (flag == 0) {//有分支则长度+1
						number++;
						flag++;
					}
					push(Lenth, number);
				}
			}
	}
	return OK;
}