（三）栈和队列

栈

定义：栈是限定仅在表尾进行插入或删除操作的线性表，表尾端称为栈顶，表尾端称为栈顶，表头端称为栈底，后进先出（Last In First Out）
抽象数据类型定义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
　ADT Stack{
　　数据对象：D={ai|ai∈ElemSet,i=1,2,...,n,n>0}
　　数据关系：Rl={<ai-1,ai>|ai-1,ai∈D，i=2,...,n}
　　基本操作：
　　InitStack(&S)
　　　　操作结果：构造一个空栈S
　　DestroyStack(&S)
　　　　初始条件：栈S已存在
　　　　操作结果：栈S清空为空栈
　　StackEmpty(S)
　　　　初始条件：栈Ｓ已存在
　　　　操作结果：若栈Ｓ为空栈，则返回true;否则false
　　StackLength(S)
　　　　初始条件：栈Ｓ已存在
　　　　操作结果：返回Ｓ的元素个数，即栈的长度
　　GetTop(S,&e)
　　　　初始条件：栈Ｓ已存在且非空
　　　　操作结果：用ｅ返回Ｓ的栈顶元素
　　Push(&S,e)
　　　　初始条件：栈Ｓ已存在
　　　　操作结果：插入元素ｅ为新的栈顶元素
　　Pop(&S,e)
　　　　初始条件：栈Ｓ已存在且非空
　　　　操作结果：删除Ｓ的栈顶元素，并用ｅ返回其值
　　StackTraverse(S,visit())
　　　　初始条件：栈Ｓ已存在且非空
　　　　操作结果：从栈底到栈顶依次对Ｓ的每个数据元素调用函数visit().一旦visit()失败，则操作失败
　　}ADT Stack

　数据结构：
1
2
3
4
5
6
7
　　　#define STACK_INIT_SIZE 100  //存储空间初始分配量
　　　#define STACKINCREMENT 10 //存储空间分配增量
　　　typedef struct{
　　　　　SElemType *　base;  //在栈构造之前和销毁之后，base的值为NULL
　　　　　SElemType *　top;  //栈顶指针
　　　　　int stacksize;　//当前已分配的存储空间，以元素为单位
　　　}SqStack;

栈的基本运算
①构造空栈　－－　S.base=(SElemType)malloc(STACK_INIT_SIZE*sizeof(SElemType));
S.top=S.base;
S.stacksize=STACK_INIT_SIZE;
②判定栈空　－－　S.top==S.base
③判定栈满　－－　S.top-S.base==S.stacksize
④进 栈　－－　*　S.top++=e
⑤出 栈　－－　e=　–S.top
⑥取 栈 顶　－－　e=*　(S.top-1)
　注意：
　　上溢：S.top-S.base>=S.stacksize
　　下溢：栈空
图示：
栈图示

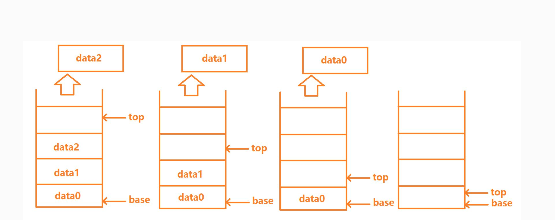
队列

　　定义：队列是一种先进先出(First In First Out)的线性表，只允许一端进行插入，另一端删除元素，允许插入的一端称为队尾，允许删除的一端称为队头
　　抽象数据类型
　　　ADT Queue{
　　　　数据对象：D={ai|ai∈ElemSet,i=1,2,…,n,n≥n}
　　　　数据关系：Rl={<ai-1,ai>|ai-1,ai∈D,i=2,…,n}
　　　　基本操作：
　　　　InitQueue(&Q)
　　　　　操作结果：构造一个空队列Q
　　　　DestroyQueue(&Q)
　　　　　初始条件：队列Q已存在
　　　　　操作结果：队列Q被销毁，不再存在
　　　　ClearQueue(Q)
　　　　　初始条件：队列Ｑ已存在
　　　　　操作结果：将Ｑ清为空队列
　　　　QueueEmpty(Q)
　　　　　初始条件：队列Ｑ已存在
　　　　　操作结果：若Ｑ为空队列，则返回true,fouze false
　　　　QueueLength(Q)
　　　　　初始条件：队列Ｑ已存在
　　　　　操作结果：返回Ｑ的元素个数，即队列的长度
　　　　GetHead(Q,&e)
　　　　　初始条件：Ｑ为非空队列
　　　　　操作结果：用ｅ返回Ｑ的队头元素
　　　　EnQueue(&Q,e)
　　　　　初始条件：队列Ｑ存在
　　　　　操作结果：插入元素ｅ为Ｑ的新的队尾元素
　　　　DeQueue(&Q,&e)
　　　　　初始条件：Ｑ为非空队列
　　　　　操作结果：删除Ｑ的队头元素，并用ｅ返回其值
　　　　QueueTraverse(Q,visit())
　　　　　初始条件：Ｑ已存在且非空
　　　　　操作结果：从队头到队尾，依次对Ｑ的每个数据元素调用函数visit()。一旦visit()失败，则操作失败
　　　}ADT Queue
　　1.单链队列：

1
2
3
4
5
6
7
8
　　　typedef struct QNode{
　　　　QElemType  data;
　　　　struct QNode  *next;
　　　}QNode,*　QueuePtr;
　　　typedef struct{
　　　　QueuePtr  front;  //队头指针
　　　　QueuePtr  rear;  //队尾指针
　　　}LinkQueue;

　　　图示：
　　　单向队列图示
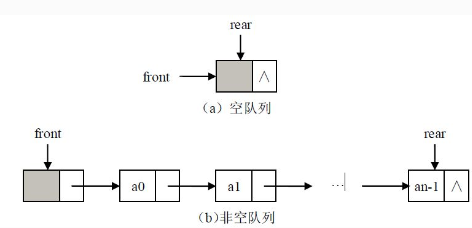
　　　基本操作：
　　　入队：
　　　
1
2
3
4
5
　　　　p=(QueuePtr)malloc(sizeof(QNode)
　　　　p->data=e;
　　　　p->next=NULL;
　　　　Q.rear->next=p;
　　　　Q.rear=p;

　　出队：
　　　
1
2
3
4
5
　　　　p=Q.front->next;
　　　　e=p->data;
　　　　Q.front->next=p->next;
　　　　if(Q.rear==p)Q.rear=Q.front;
　　　　free(p);

2.循环队列——顺序表示和实现
　　判定队列“空”或“满”
　　　①设置一个标志位
　　　②少用一个元素空间
　　　　空：Q.front==Q.rear
　　　　满：(Q.rear+1)%MAXQSIZE==Q.front
　　数据结构：
1
2
3
4
5
6
　　　#define MAXQSIZE 100  //最大队列长度
　　　typedef struct{
　　　　　QElemType  *base; //初始化的动态分配存储空间
　　　　　int front;  //头指针，若队列不空，指向队列头元素
　　　　　int rear;  //尾指针，若队列不空，指向队列尾元素的下一个位置
　　　}SqQueue;

　　图示：
　　　循环队列图示

　　　循环队列图示
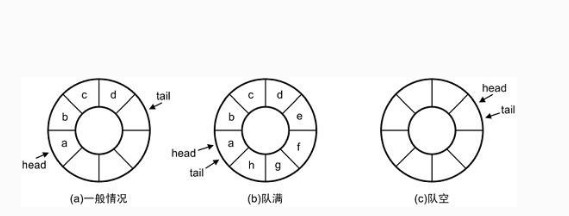
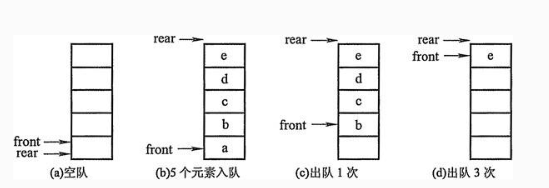
　　队列的基本操作:
　　入队:
　　

1
2
3
　　　if((Q.rear+1)%MAXQSIZE)==Q.front) return ERROR; //队列满
　　　Q.base[Q.rear]=e;
　　　Q.rear=(Q.rear+1)%MAXQSIZE;

　　出队:
　　
1
2
3
　　　if(Q.front==Q.rear) return ERROR
　　　e=Q.base[Q.front];
　　　Q.front=(Q.front+1)%MAXQSIZE;

栈代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW_ -2

typedef int Status;
typedef int SElemType;
typedef int ElemType;

#define STACK_INIT_SIZE 100
#define STACKINCREMENT 10

//------------------------顺序栈----------------------------
typedef struct{
	SElemType * base;
	SElemType * top;
	int stacksize;
}SqStack;//顺序栈

class SQSTACK{
	public:
			Status InitStack(SqStack &S);
			//构造一个空栈
			Status Destroy(SqStack &S);
			//销毁栈S，S不再存在
			Status ClearStack(SqStack &S);
			//讲S置为空栈
			Status StackEmpty(SqStack S);
			//若栈S为空栈，则返回TRUE，否则返回FALSE
			int StackLength(SqStack S);
			//返回S的元素个数，即栈的长度
			Status GetTop(SqStack S,SElemType &e);
			//若栈不空，则用e返回S的栈顶元素，并返回OK；否则返回ERROR；
			Status Push(SqStack &S,SElemType e);
			//插入元素e为新的栈顶元素
			Status Pop(SqStack &S,SElemType &e);
			//若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERROR
			Status StackTraverse(SqStack S);
			//遍历栈，满足FILO原则,即出栈
};

Status SQSTACK::InitStack(SqStack &S){
	//构造一个空栈
	S.base=(SElemType*)malloc(STACK_INIT_SIZE*sizeof(SElemType)); //栈底指针数组
	if(!S.base) exit(OVERFLOW_);//存储分配失败
	S.top=S.base;  //初始空栈的头尾指针指向相同
	S.stacksize=STACK_INIT_SIZE; //初始空栈的大小
	return OK;
}

Status SQSTACK::Destroy(SqStack &S){
	//销毁栈S，S不再存在
	free(S.base);//销毁栈底指针数组，即销毁栈
	S.top=S.base=NULL;
	return OK;
}

Status SQSTACK::ClearStack(SqStack &S){
	//讲S置为空栈

	/* while(S.top!=S.base){
		//栈不为空时，进行此操作,此情况原先数据值仍保留
		S.top--;
	}*/

	Destroy(S);//先摧毁
	InitStack(S);//后初始化
	return OK;
}

Status SQSTACK::StackEmpty(SqStack S){
	//若栈S为空栈，则返回TRUE，否则返回FALSE
	if(S.top!=S.base)return ERROR;
	return OK;
}

int SQSTACK::StackLength(SqStack S){
	//返回S的元素个数，即栈的长度
	return S.top-S.base;
}

Status SQSTACK::GetTop(SqStack S,SElemType &e){
	//若栈不空，则用e返回S的栈顶元素，并返回OK；否则返回ERROR；
	if(S.top==S.base) return ERROR;
	e=* (S.top-1);  //栈顶指针在插入元素后指向下一个空结点
	return OK;
}

Status SQSTACK::Push(SqStack &S,SElemType e){
	//插入元素e为新的栈顶元素
	if(S.top-S.base>=S.stacksize){
		//栈满，追加存储空间
		S.base=(SElemType*)realloc(S.base,(S.stacksize+STACKINCREMENT)* sizeof(SElemType));
		if(!S.base) exit(OVERFLOW_);//存储分配失败
		S.top=S.base+S.stacksize;
		S.stacksize+=STACKINCREMENT;
	}
	* S.top++=e;
	return OK;
}

Status SQSTACK::Pop(SqStack &S,SElemType &e){
	//若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERROR
	if(S.top==S.base) return ERROR;
	e=* --S.top;
	return OK;
}

Status SQSTACK::StackTraverse(SqStack S){
	//遍历栈，满足FIFO元素,即出栈
	while(S.top!=S.base){
		cout<<* --S.top<<" ";
	}
	return OK;
}


//-----------------------------链式栈-------------------------
typedef struct LNode {
	ElemType data;
	struct LNode * next;
}LNode, * LinkList; //链式栈

class LINKLIST {
	public:
			Status InitList_L(LinkList &L);
			//链表初始化
			Status CreateList_L(LinkList L, int n);
			//正序或逆序插入单链表
			Status DestroyList_L(LinkList L);
			//摧毁链表
			Status ClearList_L(LinkList L);
			//将链表重置为空表，并释放原链表的节点空间
			int ListLength_L(LinkList L);
			//返回链表长度
			Status ListInsert_L(LinkList L,ElemType e);
			//链表已存在，插入一个结点
			Status ListDelete_L(LinkList L,ElemType &e);
			//删除结点，并用e返回其值
			Status GetEleList_L(LinkList L,ElemType &e);
			//获取结点的值，并用e返回其值
			Status AlterEleList_L(LinkList L, int i, ElemType e);
			//更新结点的值
			Status Inverse_L(LinkList L);
			//遍历链表
};

Status LINKLIST::InitList_L(LinkList &L) {
	//链表初始化
	L = (LinkList)malloc(sizeof(LNode));
	if (!L) exit(OVERFLOW_);
	L->next = NULL;
	return OK;
}

Status LINKLIST::CreateList_L(LinkList L, int n) {
	//正序或逆序插入单链表
	//逆位序输入n个元素的值，建立带头结点的单链表L
	/* for(int i=n;i>0;--i){
	LinkList p=(LinkList)malloc(sizeof(LNode));//生成新结点
	if(!p)	exit(OVERFLOW_);
	//scanf("%d",&p->data);
	cin>>p->data;
	p->next=L->next;
	L->next=p;
	}*/
	//正位序插入n个元素的值，建立带头结点的单链表
	LinkList s = L;
	for (int i = n;i>0;--i) {
		LinkList p = (LinkList)malloc(sizeof(LNode));
		if (!p) exit(OVERFLOW_);
		cin >> p->data;
		p->next = s->next;
		s->next = p;
		s = p;
	}
	return OK;
}

Status LINKLIST::DestroyList_L(LinkList L) {
	//摧毁链表
	LinkList p;
	while (L->next != NULL) {
		p = L->next;
		L->next = p->next;
		free(p);
	}
	free(L); //删除头结点
	return OK;
}

Status LINKLIST::ClearList_L(LinkList L) {
	//将链表重置为空表，并释放原链表的节点空间
	LinkList p;
	while (L->next != NULL) {
		p = L->next;
		L->next = p->next;
		free(p);
	}
	//free(L);
	return OK;
}

int LINKLIST::ListLength_L(LinkList L) {
	//返回链表长度
	int length = 0;
	LinkList p = L;
	while (p->next) {
		p = p->next;
		length++;
	}
	return length;
}

Status LINKLIST::ListInsert_L(LinkList L,ElemType e) {
	//链表已存在插入一个结点
	/* if (i<1 || i>ListLength_L(L) + 1) {
		cout << "位置不合法，插入失败";
		return ERROR;
	}*/
	int locate = 0;
	LinkList p = L;
	while (p->next) {
		p = p->next;
	}
	LinkList q = (LinkList)malloc(sizeof(LNode));
	q->data = e;
	q->next = p->next;
	p->next = q;
	return OK;
}

Status  LINKLIST::ListDelete_L(LinkList L,ElemType &e) {
	//删除第i个结点，并用e返回其值
	/* if (i<1 || i>ListLength_L(L)) {
		cout << "位置不合法，删除失败";
		return ERROR;
	}*/
	int locate=0;
	LinkList p = L;
	while (p->next&&locate<ListLength_L(L)-1) {
		p = p->next;
		locate++;
	}
	e = p->next->data;
	free(p->next);//释放第i个结点
	 //cout << p->next; //测试释放后的指针指向
	p->next = NULL;
	return OK;
}

Status  LINKLIST::GetEleList_L(LinkList L,ElemType &e) {
	//获取第i个结点的值，并用e返回其值
	/* if (i<1 || i>ListLength_L(L)) {
		cout << "位置不合法，获取失败";
		return ERROR;
	}*/
	//int locate = 0;
	LinkList p = L;
	while (p->next) {
		p = p->next;
	}
	e = p->data;
	return OK;
}

Status  LINKLIST::AlterEleList_L(LinkList L, int i, ElemType e) {
	//更新第i个结点的值
	if (i<1 || i>ListLength_L(L)) {
		cout << "位置不合法，更新失败";
		return ERROR;
	}
	int locate = 0;
	LinkList p = L;
	while (p->next&&locate < i) {
		p = p->next;
		locate++;
	}
	p->data = e;
	return OK;
}

Status  LINKLIST::Inverse_L(LinkList L) {
	//遍历链表

	int i=0;
	LinkList p;
	LinkList * q=new LinkList [ListLength_L(L)];
	p=L;

	while (p->next) {
		q[i]=p = p->next;
		i++;
	}

	for(int j=i-1;j>=0;j--){
		cout << q[j]->data << " ";
	}
	delete [] q;
	return OK;
}

队列代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW_ -2

typedef int Status;
typedef int QElemType;
typedef int ElemType;

//--------------------------线性队列---------------------------
#define LIST_INIT_SIZE 100
#define LISTINCREMENT 10

typedef struct {
	ElemType * elem;
	int length;
	int listsize;
}SqList;


class LIST {
	public:
		Status InitList_Sq(SqList &L);
		//构造一个空的线性表L
		Status DestroyList(SqList &L);
		//摧毁线性表
		Status ListInsert_Sq(SqList &L, int i, ElemType e);
		//在顺序线性表L中第i个位置之前插入新的元素e
		Status ListDelete_Sq(SqList &L, int i, ElemType &e);
		//在顺序线性表L中删除第i个元素，并用e返回其值
		Status GetElem(SqList L, int i, ElemType &e);
		//线性表L已存在，1<=i<=ListLength_Sq(L)
		//用e返回L中的第i个元素
		Status ChaElem(SqList &L, int i, ElemType e);
		//用e更新线性表L的第i个元素，0<=i<=ListLength_Sq(L)
		Status ListTraverse(SqList L);
		//遍历线性表
};

Status LIST::InitList_Sq(SqList &L) {
	//构造一个空的线性表L
	L.elem = (ElemType*)malloc(LIST_INIT_SIZE * sizeof(ElemType));
	if (!L.elem) exit(OVERFLOW_);
	L.length = 0;
	L.listsize = LIST_INIT_SIZE;
	return OK;
}

Status LIST::DestroyList(SqList &L) {
	//摧毁线性表
	free(L.elem);
	//delete [] L.elem;
	//if(L.elem) exit(ERROR);
	return OK;
}

Status LIST::ListInsert_Sq(SqList &L, int i, ElemType e) {
	//在顺序线性表L中第i个位置之前插入新的元素e
	//i的合法值为1<=i<=ListLength_Sq(L)+1
	if (i<1 || i>L.length + 1) return ERROR;//i值不合法
	if (L.length >= L.listsize) {
		//当前存储空间已满，增加分配
		ElemType * newbase = (ElemType* )realloc(L.elem, (L.listsize + LISTINCREMENT) * sizeof(ElemType));
		if (!newbase) exit(OVERFLOW_);//存储分配失败
		L.elem = newbase;//新基址
		L.listsize += LISTINCREMENT;//增加存储容量
	}
	ElemType * q = &(L.elem[i - 1]);//q为插入位置
	for (ElemType * p = &(L.elem[L.length - 1]);p >= q;--p)
		* (p + 1) = * p;
	* q = e;
	++L.length;
	return OK;
}

Status LIST::ListDelete_Sq(SqList &L, int i, ElemType &e) {
	//在顺序线性表L中删除第i个元素，并用e返回其值
	//i的合法值为1<=i<=ListLength_Sq(L)+1
	if (i<1 || i>L.length + 1 || L.length == 0) return ERROR;//i值不合法
	ElemType * p = &(L.elem[i - 1]);     //p为被删除元素的位置
	e = * p;                //被删除元素的值赋给e
	ElemType * q = &(L.elem[L.length - 1]);//表尾元素的位置
	for (++p;p <= q;++p)
		* (p - 1) = * p;
	--L.length;
	return OK;
}

Status LIST::GetElem(SqList L, int i, ElemType &e) {
	//线性表L已存在，1<=i<=ListLength_Sq(L)
	//用e返回L中的第i个元素
	if (i<1 || i>L.length) return ERROR;
	e = L.elem[i - 1];
	return OK;
}

Status LIST::ChaElem(SqList &L, int i, ElemType e) {
	//用e更新线性表L的第i个元素，0<=i<=ListLength_Sq(L)
	if (i<0 || i>L.length) return ERROR;
	L.elem[i - 1] = e;
	return OK;
}

Status LIST::ListTraverse(SqList L) {
	//遍历线性表
	ElemType * p = &L.elem[0];
	ElemType * q = &L.elem[L.length - 1];
	for (p;p <= q;p++)
		printf("%d ", * p);
	printf("\n");
	return OK;
}

//-------------------------------链式队列---------------------------
typedef struct QNode {
	QElemType data;
	struct QNode * next;
}QNode,* QueuePtr;

typedef struct {
	QueuePtr front;//队头指针
	QueuePtr rear;//队尾指针
}LinkQueue;

class LINKQUEUE {
	public:
		Status InitQueue(LinkQueue &Q);
		//构造一个空队列Q
		Status DestroyQueue(LinkQueue &Q);
		//销毁队列Q，Q不再存在
		Status ClearQueue(LinkQueue &Q);
		//将Q清为空队列
		Status QueueEmpty(LinkQueue Q);
		//若队列Q为空队列，则返回TRUE，否则返回FALSE
		int QueueLength(LinkQueue Q);
		//返回Q的元素个数，即为队列的长度
		Status GetHead(LinkQueue Q, QElemType &e);
		//若队列不空，则用e返回Q的队头元素，并返回OK，否则返回ERROR
		Status EnQueue(LinkQueue &Q, QElemType e);
		//插入元素e为Q的新队尾元素
		Status DeQueue(LinkQueue &Q, QElemType &e);
		//若队列不空则删除Q的队头元素，用e返回其值，并返回OK，否则返回ERROR
		Status QueueTraverse(LinkQueue Q);
		//若队列不空则遍历队列
};

Status LINKQUEUE::InitQueue(LinkQueue &Q) {
	//构造一个空队列Q
	Q.front = Q.rear = (QueuePtr)malloc(sizeof(QNode));
	if (!Q.front)exit(OVERFLOW_);
	Q.front->next = NULL;
	return OK;
}

Status LINKQUEUE::DestroyQueue(LinkQueue &Q) {
	//摧毁队列Q
	while (Q.front) {
		Q.rear = Q.front->next;
		free(Q.front);
		Q.front = Q.rear;
	}
	return OK;
}

Status LINKQUEUE::ClearQueue(LinkQueue &Q) {
	//清空队列
	QueuePtr p = Q.front->next;
	QueuePtr q;
	while (p) {
		q = p->next;
		free(p);
		p = q;
	}
	Q.front->next = NULL;
	Q.rear = Q.front;
	return OK;
}

Status LINKQUEUE::QueueEmpty(LinkQueue Q) {
	//判断队列空与否
	if(!QueueLength(Q))
		return OK;
	return ERROR;
}

int LINKQUEUE::QueueLength(LinkQueue Q) {
	//返回Q的元素个数，即为队列的长度
	QueuePtr p = Q.front;
	int length = 0;
	while (p->next) {
		p = p->next;
		length++;
	}
	return length;
}

Status LINKQUEUE::GetHead(LinkQueue Q, QElemType &e) {
	//获取队头元素
	if (QueueEmpty(Q))return ERROR;
	e = Q.front->next->data;
	return OK;
}

Status LINKQUEUE::EnQueue(LinkQueue &Q, QElemType e) {
	//插入元素e至队列尾
	QueuePtr p = (QueuePtr)malloc(sizeof(QNode));
	if (!p)exit(OVERFLOW_);
	p->data = e;
	p->next = NULL;
	Q.rear->next = p;
	Q.rear = p;
	return OK;
}

Status LINKQUEUE::DeQueue(LinkQueue &Q, QElemType &e) {
	//若队列不空则删除Q的队头元素，用e返回其值，并返回OK，否则返回ERROR
	if (Q.front == Q.rear)return ERROR;
	QueuePtr p = Q.front->next;
	e = p->data;
	Q.front->next = p->next;
	if (Q.rear == p)Q.rear = Q.front;
	free(p);
	return OK;
}

Status LINKQUEUE::QueueTraverse(LinkQueue Q) {
	QueuePtr p = Q.front->next;
	if (QueueEmpty(Q))return ERROR;
	while (p) {
		cout << p->data << " ";
		p = p->next;
	}
	return OK;
}
赏

Thank you for inviting me to have candy.

支付宝
微信

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

做一个安静细微的人，<br> 于角落里自在开放，<br> 默默悦人，<br> 却始终不引起过分热闹的关注，<br> 保有独立而随意的品格，<br> 这就很好。<br><br> Stick to what you insist on,<br> believe what you believe!<br> Life hastily for decades,<br> do what I can!