算法基础

2017-08-02

第一章枚举

Perfect Cubes

Description
For hundreds of years Fermat’s Last Theorem, which stated simply that for n > 2 there exist no integers a, b, c > 1 such that a^n = b^n + c^n, has remained elusively unproven. (A recent proof is believed to be correct, though it is still undergoing scrutiny.) It is possible, however, to find integers greater than 1 that satisfy the “perfect cube” equation $a^3 = b^3 + c^3 + d^3$ (e.g. a quick calculation will show that the equation $12^3 = 6^3 + 8^3 + 10^3$ is indeed true). This problem requires that you write a program to find all sets of numbers {a,b,c,d} which satisfy this equation for a <= N.
Input
One integer N (N <= 100).
OutPut
The output should be listed as shown below, one perfect cube per line, in non-decreasing order of a (i.e. the lines should be sorted by their a values). The values of b, c, and d should also be listed in non-decreasing order on the line itself. There do exist several values of a which can be produced from multiple distinct sets of b, c, and d triples. In these cases, the triples with the smaller b values should be listed first.
Sample Input
24
Sample OutPut
Cube = 6, Triple = (3,4,5)
Cube = 12, Triple = (6,8,10)
Cube = 18, Triple = (2,12,16)
Cube = 18, Triple = (9,12,15)
Cube = 19, Triple = (3,10,18)
Cube = 20, Triple = (7,14,17)
Cube = 24, Triple = (12,16,20)
Procedure

/*

文件名称：完美立方.cpp

解题思路：
四重循环枚举a,b,c,d，a在最外层，d在最里层，每一层都是从小到大枚举
b<=c<=d
a枚举范围[2,N]
b范围[2,a-1]
c范围[b,a-1]
d范围[c,a-1]

完成日期：2017.08.02

*/
#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
	int N;
	cin >> N;
	for (int a = 2; a <= N; a++)
	{
		for (int b = 2; b < a; b++)
		{
			for (int c = b; c < a; c++)
			{
				for (int d = c; d < a; d++)
				{
					if (a*a*a == b*b*b + c*c*c + d*d*d)
					{
						printf("Cube = %d, Triple = (%d,%d,%d)\n", a, b, c, d);
					}
				}
			}
		}
	}
	return 0;
}

Biorhythms

Description
Some people believe that there are three cycles in a person’s life that start the day he or she is born. These three cycles are the physical, emotional, and intellectual cycles, and they have periods of lengths 23, 28, and 33 days, respectively. There is one peak in each period of a cycle. At the peak of a cycle, a person performs at his or her best in the corresponding field (physical, emotional or mental). For example, if it is the mental curve, thought processes will be sharper and concentration will be easier.
Since the three cycles have different periods, the peaks of the three cycles generally occur at different times. We would like to determine when a triple peak occurs (the peaks of all three cycles occur in the same day) for any person. For each cycle, you will be given the number of days from the beginning of the current year at which one of its peaks (not necessarily the first) occurs. You will also be given a date expressed as the number of days from the beginning of the current year. You task is to determine the number of days from the given date to the next triple peak. The given date is not counted. For example, if the given date is 10 and the next triple peak occurs on day 12, the answer is 2, not 3. If a triple peak occurs on the given date, you should give the number of days to the next occurrence of a triple peak.
Input
You will be given a number of cases. The input for each case consists of one line of four integers p, e, i, and d. The values p, e, and i are the number of days from the beginning of the current year at which the physical, emotional, and intellectual cycles peak, respectively. The value d is the given date and may be smaller than any of p, e, or i. All values are non-negative and at most 365, and you may assume that a triple peak will occur within 21252 days of the given date. The end of input is indicated by a line in which p = e = i = d = -1.
Output
For each test case, print the case number followed by a message indicating the number of days to the next triple peak, in the form:
Case 1: the next triple peak occurs in 1234 days.
Use the plural form “days” even if the answer is 1.
Sample Input
0 0 0 0
0 0 0 100
5 20 34 325
4 5 6 7
283 102 23 320
203 301 203 40
-1 -1 -1 -1
Sample Output
Case 1: the next triple peak occurs in 21252 days.
Case 2: the next triple peak occurs in 21152 days.
Case 3: the next triple peak occurs in 19575 days.
Case 4: the next triple peak occurs in 16994 days.
Case 5: the next triple peak occurs in 8910 days.
Case 6: the next triple peak occurs in 10789 days.
Procedure

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：生理周期.cpp

解题思路：
从d+1填开始，一直试到第21252天，对于其中每个日子k，看是否满足
(k-p)%23==0&&(k-e)%28==0&&（k-i)%33==0
如何变快？
找到两个相邻高峰日子周期即可
先找到一个体力高峰日子，然后按其周期间隔递增
体力和情商高峰重叠时，按其两者周期乘积递增

完成日期：2017.08.02

*/
#include<iostream>
using namespace std;
const int N = 21252;
int main()
{
	int p, e, i, d, caseNo = 0;
	while (cin >> p >> e >> i >> d&&p != -1)
	{
		++caseNo;
		int k;
		for (k = d + 1; (k - p) % 23; ++k); //找到第一个体力高峰
		for (; (k - e) % 28; k += 23);     //找到体力和情商高峰重叠
		for (; (k - i) % 33; k += 23 * 28); //找到三者重叠
		cout << "Case " << caseNo << ": the next triple peak occurs in " << k - d << " days." << endl;
	}
	return 0;
}

Meet Doctor

Description
It seems that Borya is seriously sick. He is going visit n doctors to find out the exact diagnosis. Each of the doctors needs the information about all previous visits, so Borya has to visit them in the prescribed order (i.e. Borya should first visit doctor 1, then doctor 2, then doctor 3 and so on). Borya will get the information about his health from the last doctor.
Doctors have a strange working schedule. The doctor i goes to work on the si-th day and works every di day. So, he works on days si, si + di, si + 2di, ….
The doctor’s appointment takes quite a long time, so Borya can not see more than one doctor per day. What is the minimum time he needs to visit all doctors?
Input
First line contains an integer n — number of doctors (1 ≤ n ≤ 1000).
Next n lines contain two numbers si and di (1 ≤ si, di ≤ 1000).
Output
Output a single integer — the minimum day at which Borya can visit the last doctor.
Precedure

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：Meet Doctor

解题思路：
见代码

版本：1.0
作者：Louris
完成日期：2017.11.20
*/
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<cstdio>
using namespace std;
struct Doctor
{
	int firstDay;
	int intervalDay;
	Doctor(int f,int i):firstDay(f),intervalDay(i){}
};
int main()
{
	int n;
	cin>>n;
	queue<Doctor> que;
	for(int i=0;i<n;i++)
	{
		int a,b;
		cin>>a>>b;
		que.push(Doctor(a,b));
	}
	int lastVisitDay=0;
	while(!que.empty())
	{
		Doctor tmp=que.front();
		que.pop();
		if(tmp.firstDay>lastVisitDay)
		{
			lastVisitDay=tmp.firstDay;
		}
		else
		{
			for(int i=tmp.firstDay;;i+=tmp.intervalDay)
			{
				if(i>lastVisitDay)
				{
					lastVisitDay=i;
					break;
				}
			}
		}
	}
	cout<<lastVisitDay<<endl;
	return 0;
}

Counterfeit Dollar

Description
Sally Jones has a dozen Voyageur silver dollars. However, only eleven of the coins are true silver dollars; one coin is counterfeit even though its color and size make it indistinguishable from the real silver dollars. The counterfeit coin has a different weight from the other coins but Sally does not know if it is heavier or lighter than the real coins.
Happily, Sally has a friend who loans her a very accurate balance scale. The friend will permit Sally three weighings to find the counterfeit coin. For instance, if Sally weighs two coins against each other and the scales balance then she knows these two coins are true. Now if Sally weighs
one of the true coins against a third coin and the scales do not balance then Sally knows the third coin is counterfeit and she can tell whether it is light or heavy depending on whether the balance on which it is placed goes up or down, respectively.
By choosing her weighings carefully, Sally is able to ensure that she will find the counterfeit coin with exactly three weighings.
Input
The first line of input is an integer n (n > 0) specifying the number of cases to follow. Each case consists of three lines of input, one for each weighing. Sally has identified each of the coins with the letters A–L. Information on a weighing will be given by two strings of letters and then one of the words “up”, “down”, or “even”. The first string of letters will represent the coins on the left balance; the second string, the coins on the right balance. (Sally will always place the same number of coins on the right balance as on the left balance.) The word in the third position will tell whether the right side of the balance goes up, down, or remains even.
Sample Input
1
ABCD EFGH even
ABCI EFJK up
ABIJ EFGH even
Sample Output
K is the counterfeit coin and it is light.
Procedure

/*

文件名称：称硬币.cpp

解题思路：
对于每一枚硬币先假设它是轻的，看这样是否符合称量结果。如果符合，问题即解决。如果不符合，就假设它是重的，看是否符合称量结果。把所有硬币都试一遍，一定能找到特殊硬币。
如果当测的硬币是轻的，那么根据三次测量结果：
①even，则天平两侧不能出现，否则IsFake返回false
②up，则天平右边翘起，所以当测硬币在天平右边，如果不在，IsFake返回false
③down，则天平右边偏重，所以当测硬币在天平左侧，如果不在，IsFake返回false
④如果三次结果都满足，那么IsFake返回ture
同理，
如果当测硬币是重的，那么根据三次测量结果：
①even，则天平两侧不能出现，否则IsFake返回false
②up，则天平右边更轻，所以当测硬币在天平左边，如果不在，IsFake返回false
③down，则天平右边更重，所以当测硬币在天平右边，如果不在，IsFake返回false
④如果三次结果都满足，那么IsFake返回true

完成日期：2017.08.02

*/
#include<iostream>
using namespace std;
char Left[3][7]; //天平左边硬币
char Right[3][7]; //天平右边硬币
char Result[3][7]; //结果
bool IsFake(char c, bool light)
{
	//light为真表示假设假币为轻，否则表示假设假币为重
	for (int i = 0; i < 3; i++)
	{
		char *pLeft, *pRight; //指向天平两边的字符串
		if(light)
		{
			pLeft = Left[i];
		    pRight = Right[i];
		}
		else  //如果假设假币是重的，则把称量结果左右对换
		{
			pLeft = Right[i];
			pRight = Left[i];
		}
		switch (Result[i][0]) //天平右边的情况
		{
		case 'u':
			if (strchr(pRight, c) == NULL)
			{
				return false;
			}
			break;
		case 'e':
			if (strchr(pLeft, c) || strchr(pRight, c))
			{
				return false;
			}
			break;
		case 'd':
			if (strchr(pLeft, c) == NULL)
			{
				return false;
			}
			break;
		}
	}
	return true;
}
int main()
{
	int t;
	cin >> t;
	while (t--)
	{
		for (int i = 0; i < 3; i++)
		{
			cin >> Left[i] >> Right[i] >> Result[i];
		}
		for (char c = 'A'; c <= 'L'; c++)
		{
			if (IsFake(c, true))
			{
				cout << c << " is the counterfeit coin and it is light.\n";
				break;
			}
			else if(IsFake(c,false))
			{
				cout << c << " is the counterfeit coin and it is heavy.\n";
				break;
			}
		}
	}
	return 0;
}

#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<cstdio>
using namespace std;
string Left[3];
string Right[3];
string Result[3];

bool isLight(char c)
{
	for (int i = 0; i < 3; i++)
	{
		switch (Result[i][0])
		{
		case 'u':
			if (Right[i].find(c, 0)==-1)
			{
				return false;
			}
			break;
		case 'e':
			if (Left[i].find(c, 0)!=-1 || Right[i].find(c, 0)!=-1)
			{
				return false;
			}
			break;
		case 'd':
			if (Left[i].find(c, 0)==-1)
			{
				return false;
			}
			break;
		}
	}
	return true;
}
bool isHeavy(char c)
{
	for (int i = 0; i < 3; i++)
	{
		switch (Result[i][0])
		{
		case 'u':
			if (Left[i].find(c, 0) == -1)
			{
				return false;
			}
			break;
		case 'e':
			if (Left[i].find(c, 0) != -1 || Right[i].find(c, 0) != -1)
			{
				return false;
			}
			break;
		case 'd':
			if (Right[i].find(c, 0) == -1)
			{
				return false;
			}
			break;
		}
	}
	return true;
}
bool isFake(char c, bool isLight)
{

	for (int i = 0; i < 3; i++)
	{
		string pLeft, pRight;
		if (!isLight)
		{
			pRight = Left[i];
			pLeft = Right[i];
		}
		else
		{
			pRight = Right[i];
			pLeft = Left[i];
		}
		switch (Result[i][0])
		{
		case 'u':
			if (pRight.find(c, 0) == -1)
			{
				return false;
			}
			break;
		case 'e':
			if (pLeft.find(c, 0) != -1 || pRight.find(c, 0) != -1)
			{
				return false;
			}
			break;
		case 'd':
			if (pLeft.find(c, 0) == -1)
			{
				return false;
			}
			break;
		}
	}
	return true;
}
int main()
{
	int n;
	cin >> n;
	while (n--)
	{
		for (int i = 0; i < 3; i++)
		{
			cin >> Left[i] >> Right[i] >> Result[i];
			//cout << Left[i] << "||" << Right[i] << "||" << Result[i]<<endl;
		}
		for (char c = 'A'; c <= 'L'; c++)
		{
			if (isFake(c,true))
			{
				cout << c << " is the counterfeit coin and it is light." << endl;
				break;
			}
			else if(isFake(c,false))
			{
				cout << c << " is the counterfeit coin and it is heavy." << endl;
				break;
			}
		}
	}
	return 0;
}

Extended Lights Out

Description
In an extended version of the game Lights Out, is a puzzle with 5 rows of 6 buttons each (the actual puzzle has 5 rows of 5 buttons each). Each button has a light. When a button is pressed, that button and each of its (up to four) neighbors above, below, right and left, has the state of its light reversed. (If on, the light is turned off; if off, the light is turned on.) Buttons in the corners change the state of 3 buttons; buttons on an edge change the state of 4 buttons and other buttons change the state of 5. For example, if the buttons marked X on the left below were to be pressed,the display would change to the image on the right.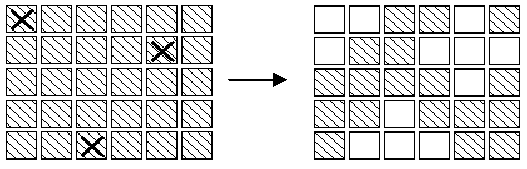
ExtendedLightsOut1
The aim of the game is, starting from any initial set of lights on in the display, to press buttons to get the display to a state where all lights are off. When adjacent buttons are pressed, the action of one button can undo the effect of another. For instance, in the display below, pressing buttons marked X in the left display results in the right display.Note that the buttons in row 2 column 3 and row 2 column 5 both change the state of the button in row 2 column 4,so that, in the end, its state is unchanged.
ExtendedLightsOut2
Note:

It does not matter what order the buttons are pressed.
If a button is pressed a second time, it exactly cancels the effect of the first press, so no button ever need be pressed more than once.
As illustrated in the second diagram, all the lights in the first row may be turned off, by pressing the corresponding buttons in the second row. By repeating this process in each row, all the lights in the first
four rows may be turned out. Similarly, by pressing buttons in columns 2, 3 ?, all lights in the first 5 columns may be turned off.
Write a program to solve the puzzle.

Input
The first line of the input is a positive integer n which is the number of puzzles that follow. Each puzzle will be five lines, each of which has six 0 or 1 separated by one or more spaces. A 0 indicates that the light is off, while a 1 indicates that the light is on initially.
Output
For each puzzle, the output consists of a line with the string: “PUZZLE #m”, where m is the index of the puzzle in the input file. Following that line, is a puzzle-like display (in the same format as the input) . In this case, 1’s indicate buttons that must be pressed to solve the puzzle, while 0 indicate buttons, which are not pressed. There should be exactly one space between each 0 or 1 in the output puzzle-like display.
Sample Input
2
0 1 1 0 1 0
1 0 0 1 1 1
0 0 1 0 0 1
1 0 0 1 0 1
0 1 1 1 0 0
0 0 1 0 1 0
1 0 1 0 1 1
0 0 1 0 1 1
1 0 1 1 0 0
0 1 0 1 0 0
Sample OutPut
PUZZLE #1
1 0 1 0 0 1
1 1 0 1 0 1
0 0 1 0 1 1
1 0 0 1 0 0
0 1 0 0 0 0
PUZZLE #2
1 0 0 1 1 1
1 1 0 0 0 0
0 0 0 1 0 0
1 1 0 1 0 1
1 0 1 1 0 1
Procedure

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：熄灯问题.cpp

解题思路：
第一思路：枚举所有可能的按钮（开关）状态，对每个状态计算一下最后灯的情况，看是否都熄灭
①每个按钮有两种状态
②一共有30个开关，那么状态数是2^30，太多，会超时
第二思路：如果存在某个局部，一旦这个局部状态被确定，那么剩余其他部分的状态只能是确定的一种，或者不多的n种，那么就只需枚举这个局部的状态即可
局部：
经过观察，发现第1行就是这样的一个“局部”
①因为第1行的各开关状态确定的情况下，这些开关作用过后，将导致第1行某些灯是亮的，某些灯是灭的
要灭第1行某个亮着的灯（假设位于第i列），那么唯一的办法就是按下第2行第i列的开关。
（因为第1行开关已经使用，第三行开关不影响第1行）
②那么第1行却不熄灭，第2行的状态也有可能有未灭的灯，那么得考虑第3行
③以此类推，若最后一行的开关使用完后，灯全部熄灭，那么合理，否则不合理
④两次按开关按钮的效果抵消。

完成日期：2017.08.02
*/

#include<iostream>
#include<memory>
#include<string>
#include<cstring>
#include<iostream>
using namespace std;
char oriLights[5];
char lights[5];
char result[5];

int GetBit(char c, int i)
{
	return (c >> i) & 1; //获取第i位
}

void SetBit(char &c, int i, int v)
{
	if (v)
	{
		c |= (1 << i); //按位或运算使得对应bit位为1
	}
	else
	{
		c &= ~(1 << i);  //按位与运算使得对应bit位为0
		//c &= 0 << i;
	}
}

void FlipBit(char &c, int i)
{
	c ^= (1 << i);  //按位异或运算
}

void OutputResult(int t, char result[])  //输出函数
{
	cout << "PUZZLE #" << t << endl;
	for (int i = 0; i < 5; ++i)
	{
		for (int j = 0; j < 6; ++j)
		{
			cout << GetBit(result[i], j);
			if (j < 5)
			{
				cout << " ";
			}
			cout << endl;
		}
	}
}


int main()
{
	int T;
	cout << (int)oriLights[0] << " " << oriLights[1];
	cin >> T;
	for (int t = 1; t <= T; ++t)
	{
		for (int i = 0; i < 5; ++i) //初始化
		{
			for (int j = 0; j < 6; ++j)
			{
				int s;
				cin >> s;
				SetBit(oriLights[i], j, s);
			}
		}

		for (int n = 0; n < 64; ++n) //每行6列，6位2^6种状态
		{
			int switchs = n;
			memcpy(lights, oriLights, sizeof(oriLights)); //复制数组
			for (int i = 0; i < 5; ++i)  //按行枚举
			{
				result[i] = switchs;   //枚举初始化
				for (int j = 0; j < 6; ++j) //同一行的灯进行处理
				{
					if (GetBit(switchs, j)) //开关被按下
					{
						if (j > 0)
						{
							FlipBit(lights[i], j-1);
						}
						FlipBit(lights[i], j);
						if (j < 5)
						{
							FlipBit(lights[i], j + 1);
						}
					}
				}
				if (i < 4)//处理下一行
				{
					lights[i + 1] ^= switchs;
				}
				switchs = lights[i]; //第i行的灯状态就是下一行的开关状态
			}
			if (lights[4] == 0)  //判断是否最后一行各位都为0，如果是则代表全部熄灭，否则不满足题意
			{
				OutputResult(t, result);
				break;
			}
		}
	}
	return 0;
}

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：熄灯问题_STL.cpp

解题思路：
第一思路：枚举所有可能的按钮（开关）状态，对每个状态计算一下最后灯的情况，看是否都熄灭
①每个按钮有两种状态
②一共有30个开关，那么状态数是2^30，太多，会超时
第二思路：如果存在某个局部，一旦这个局部状态被确定，那么剩余其他部分的状态只能是确定的一种，或者不多的n种，那么就只需枚举这个局部的状态即可
局部：
经过观察，发现第1行就是这样的一个“局部”
①因为第1行的各开关状态确定的情况下，这些开关作用过后，将导致第1行某些灯是亮的，某些灯是灭的
要灭第1行某个亮着的灯（假设位于第i列），那么唯一的办法就是按下第2行第i列的开关。
（因为第1行开关已经使用，第三行开关不影响第1行）
②那么第1行却不熄灭，第2行的状态也有可能有未灭的灯，那么得考虑第3行
③以此类推，若最后一行的开关使用完后，灯全部熄灭，那么合理，否则不合理
④两次按开关按钮的效果抵消。


当前版本：1.0
作    者：Louris
完成日期：2017.08.03
*/

#include<iostream>
#include<bitset>
#include<memory>
using namespace std;
bitset<6> OriLights[5];
bitset<6> Lights[5];
bitset<6> Result[5];

int main()
{
	int T;
	cin >> T;
	for (int t = 1; t <= T; t++)
	{
		for (int i = 0; i < 5; i++)
		{
			for (int j = 0; j < 6; j++)
			{
				int s;
				cin >> s;
				OriLights[i][j] = s;
			}
		}

		for (int n = 0; n < 64; n++)
		{
			bitset<6> switchs = n;
			memcpy(Lights, OriLights, sizeof(OriLights));
			for (int i = 0; i < 5; i++)
			{
				Result[i] = switchs;
				for (int j = 0; j < 6; j++)//处理当行
				{
					if (switchs[j] == 1)
					{
						if (j > 0)
						{
							Lights[i].flip(j-1);
						}
						Lights[i].flip(j);
						if (j < 5)
						{
							Lights[i].flip(j + 1);
						}
					}
				}
				if (i < 4)
				{
					Lights[i + 1] ^= switchs;
				}
				switchs = Lights[i];
			}
			if (Lights[4] == 0)
			{
				cout << "PUZZLE #" << t << endl;
				for (int i = 0; i < 5; i++)
				{
					for (int j = 0; j < 6; j++)
					{
						cout << Result[i][j];
						if (j < 5)
						{
							cout << " ";
						}
					}
					cout << endl;
				}
			}
		}
	}
	return 0;
}

Painter’s Problem

Description
There is a square wall which is made of n*n small square bricks. Some bricks are white while some bricks are yellow. Bob is a painter and he wants to paint all the bricks yellow. But there is something wrong with Bob’s brush. Once he uses this brush to paint brick (i, j), the bricks at (i, j), (i-1, j), (i+1, j), (i, j-1) and (i, j+1) all change their color. Your task is to find the minimum number of bricks Bob should paint in order to make all the bricks yellow.
![Painter’s Problem图示](/assets/img/algorithm/Painter’s Problem.jpg)
Input
The first line contains a single integer t (1 <= t <= 20) that indicates the number of test cases. Then follow the t cases. Each test case begins with a line contains an integer n (1 <= n <= 15), representing the size of wall. The next n lines represent the original wall. Each line contains n characters. The j-th character of the i-th line figures out the color of brick at position (i, j). We use a ‘w’ to express a white brick while a ‘y’ to express a yellow brick.
Output
For each case, output a line contains the minimum number of bricks Bob should paint. If Bob can’t paint all the bricks yellow, print ‘inf’.
Sample Input
2
3
yyy
yyy
yyy
5
wwwww
wwwww
wwwww
wwwww
wwwww
Sample Output
0
15
Procedure

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：画家问题.cpp

解题思路：
典型的枚举，详细思路参见熄灯问题，这里不再过多叙述

当前版本：1.0
作    者：Louris
完成日期：2017.09.23
*/
#include<iostream>
#include<algorithm>
#include<memory>
#include<cstring>
#include<string>
#include<bitset>
#include<cmath>
using namespace std;
bitset<15> oriPaint[15];
bitset<15> tmpPaint[15];
int nCount;
int t;
int N;
int main()
{
	cin >> t;
	while (t--)
	{
		cin >> N;
    memset(oriPaint, 0, sizeof(oriPaint));
		memset(tmpPaint, 0, sizeof(tmpPaint));
		for (int i = 0; i < N; i++)
		{
			for (int j = 0; j < N; j++)
			{
				char tmp;
				cin >> tmp;
				int x;
				(tmp == 'y') ? x = 0 : x = 1;
				oriPaint[i][j] = x;
			}
		}
		nCount = 1 << 30;
		for (int n = 0; n < (1 << N); n++)
		{
			int sum = 0;
			bitset<15> switchs = n;
			memcpy(tmpPaint, oriPaint, sizeof(oriPaint));
			for (int i = 0; i < N; i++)
			{
				if (sum > nCount)//剪枝
				{
					break;
				}
				sum += switchs.count();
				for (int j = 0; j < N; j++)
				{
					if (switchs[j] == 1)
					{
						if (j > 0)
						{
							tmpPaint[i].flip(j - 1);
						}
						tmpPaint[i].flip(j);
						if (j < N - 1)
						{
							tmpPaint[i].flip(j + 1);
						}
					}
				}
				if (i < N - 1)
				{
					tmpPaint[i+1] ^= switchs;
				}
				switchs = tmpPaint[i];
			}
			if (tmpPaint[N - 1] == 0)
			{
				nCount = min(sum, nCount);
			}
		}
		if (nCount != 1 << 30)
		{
			cout << nCount << endl;
		}
		else
		{
			cout << "inf" << endl;
		}
	}
	return 0;
}

特殊密码锁

描述
有一种特殊的二进制密码锁，由n个相连的按钮组成（n<30），按钮有凹/凸两种状态，用手按按钮会改变其状态。

然而让人头疼的是，当你按一个按钮时，跟它相邻的两个按钮状态也会反转。当然，如果你按的是最左或者最右边的按钮，该按钮只会影响到跟它相邻的一个按钮。

当前密码锁状态已知，需要解决的问题是，你至少需要按多少次按钮，才能将密码锁转变为所期望的目标状态。

输入
两行，给出两个由0、1组成的等长字符串，表示当前/目标密码锁状态，其中0代表凹，1代表凸。

输出
至少需要进行的按按钮操作次数，如果无法实现转变，则输出impossible。

样例输入
011
000

样例输出
1

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：特殊密码锁.cpp

解题思路：
同上一题的思路，每行2^3种可能，那么按法也有那么多种，枚举即可
上一题中，由于每行各位之间按钮按下后即确定，但会对下一行产生影响
本题中，无论从哪一端开始进行，前一位的结果会反过来对后一位的按钮设置产生影响

当前版本：1.0
作    者：Louris
完成日期：2017.08.03
*/

#include<iostream>
#include<string>
#include<bitset>
#include<memory>
#include<cmath>
using namespace std;

bitset<30> OriLock;
bitset<30> Result;
bitset<30> Lock;
string A, B;

int main()
{
	int sum, min,flag;
	while (cin >> A>> B)
	{
		sum = min = flag = 0;
		OriLock.reset();
		Result.reset();
		Lock.reset();
		for (unsigned int i = 0;i<A.size();i++) //输入
		{
			OriLock[0] = A[i] - '0';
			Result[0] = B[i] - '0';
			if (i != A.size() - 1)
			{
				OriLock <<= 1;
				Result <<= 1;
			}

		}
		//cout << OriLock << " " << Result << endl;
		for (unsigned int n = 0; n < 2; n++)
		{
			Lock = OriLock;
			//cout << Lock << endl;;
			bitset<30> switchs = n;
			//cout << switchs << endl;
			for (unsigned int i = 0; i < A.size(); i++)
			{
				if (switchs[i] == 1)
				{
					if (i > 0) {
						Lock.flip(i - 1);
					}
					Lock.flip(i);
					if (i < A.size()-1)
					{
						Lock.flip(i + 1);
					}
				}
				if (Lock[i] != Result[i])
				{
					switchs[i+1] = 1;
				}
				else
				{
					switchs[i+1] = 0;
				}
			}

			if (Lock == Result)
			{
				if (flag == 0)
				{
					sum = min = switchs.count();
					flag++;
				}
				else
				{
					sum = switchs.count();
					if (sum < min)
					{
						min = sum;
					}
				}

			}
		}

		if (min == 0 && Result != OriLock)
		{
			cout << "impossible" << endl;
		}
		else
		{
			cout << min << endl;
		}
	}
	return 0;
}

#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<cmath>
#include<memory>
#include<bitset>
using namespace std;
bitset<30> oriLock;
bitset<30> Lock;
bitset<30> Result;
string A, B;
int main()
{
	while (cin >> A >> B)
	{
		for (unsigned int i = 0; i < A.length(); i++)
		{
			oriLock[i] = A[i]-'0';
			Result[i] = B[i]-'0';
		}
		int Min = 1 << 30;
		for (int n = 0; n < 2; n++)
		{
			int sum = 0;
			bitset<1> switchs = n;
			Lock = oriLock;
			for (unsigned int i = 0; i < A.length(); i++)
			{
				if (switchs == 1)
				{
					sum++;
					if (i > 0)
					{
						Lock.flip(i - 1);
					}
					Lock.flip(i);
					if (i < A.length() - 1)
					{
						Lock.flip(i + 1);
					}
				}
				if (i < A.length() - 1)
				{
					switchs = Lock[i] ^ Result[i];
				}
			}
			if (Lock == Result)
			{
				Min = min(Min, sum);
			}
		}
		if (Min != 1 << 30)
		{
			cout << Min << endl;
		}
		else
		{
			cout << "impossible" << endl;
		}
	}
	return 0;
}

拨钟问题

描述

|-------|    |-------|    |-------|
|       |    |       |    |   |   |
|---O   |    |---O   |    |   O   |
|       |    |       |    |       |
|-------|    |-------|    |-------|
    A            B            C    

|-------|    |-------|    |-------|
|       |    |       |    |       |
|   O   |    |   O   |    |   O   |
|   |   |    |   |   |    |   |   |
|-------|    |-------|    |-------|
    D            E            F    

|-------|    |-------|    |-------|
|       |    |       |    |       |
|   O   |    |   O---|    |   O   |
|   |   |    |       |    |   |   |
|-------|    |-------|    |-------|
    G            H            I

有9个式中，排成3×3的矩阵
A B C
D E F
G H I
现在需要用最少的移动，将9个时钟的指针都拨到12点的位置。共允许有9种不同的移动。如下表所示，每个移动会将若干个时钟的指针沿顺时针方向拨动90度。
移动影响的时钟
1 ABDE
2 ABC
3 BCEF
4 ADG
5 BDEFH
6 CFI
7 DEGH
8 GHI
9 EFHI
输入
9个整数，表示各时钟指针的起始位置，相邻两个整数之间用单个空格隔开。其中，0=12点、1=3点、2=6点、3=9点。
输出
输出一个最短的移动序列，使得9个时钟的指针都指向12点。按照移动的序号从小到大输出结果。相邻两个整数之间用单个空格隔开。
样例输入
3 3 0
2 2 2
2 1 2
样例输出
4 5 8 9
程序

 /*
Copyright(c)2017, Louris
All rights reserved.

文件名称：拨钟问题.cpp

解题思路：
用一位数组表示九个钟
A B C   0 1 2
D E F   3 4 5
G H I   6 7 8

移动    影响的时钟
1         ABDE      0 1 3 4
2         ABC       0 1 2
3         BCEF      1 2 4 5

4         ADG       0 3 6
5         BDEFH     1 3 4 5 7
6         CFI       2 5 8

7         DEGH      3 4 6 7
8         GHI       6 7 8
9         EFHI      4 5 7 8

类似前几题，此题相比于之前的开关两种状态循环而言，将有0，1，2，3种状态
同样讨论局部：
-第一行A B C，利用①②③移动操作，将有4^3种情况，它们相互不影响；
-完成上一步操作后，有可能A B C还没有指向12点，那么在第二行D E F受影响改变指针后，
可发现④⑤⑥移动操作仅分别对A、B、C进行移动操作，故④⑤⑥移动操作数将由上一次的操作确定，
因为这是唯一能够使得A B C指向12点的操作，故而确定④⑤⑥操作数；
-同理，完成上一步操作后，第三行G H I受影响而改变，在上一步操作的基础上（第一行已经指向12点），
第二行的D E F挂钟未必就是指向12点的，那么⑦⑨移动操作数确定，因为只有它们能够改变D E F指向，
但是⑦⑨操作数由D F状态决定，因为E不定
-此时E G H I状态不定，而⑧移动操作只能改变G H I，所以此时先判断E是否指向12点，
如果不是，直接结束，
如果是，进行⑧操作，判断G H I是否都指向12点，是则退出，否则直至⑧枚举完毕。


当前版本：1.0
作    者：Louris
完成日期：2017.08.04
*/

#include <iostream>
#include <algorithm>
#include<climits>
#include<cstring>
#include<vector>
using namespace std;
int OriLock[9];
int Lock[9];
int Result[9];
vector<int> v;
int sum;
int Min;

int main()
{
	//数据输入
	for (int i = 0; i < 9; i++)
	{
		cin >> OriLock[i];
	}

	//数据处理
	Min = INT_MAX;
	for (int move_one = 0; move_one < 4; move_one++) //①移动操作
	{
		for (int move_two = 0; move_two < 4; move_two++) //②移动操作
		{
			for (int move_three = 0; move_three < 4; move_three++) //③移动操作
			{
				sum = 0;
				memcpy(Lock, OriLock, sizeof(OriLock));

				//修改①相关钟指向
				Lock[0] = (Lock[0] + move_one) % 4;
				Lock[1] = (Lock[1] + move_one) % 4;
				Lock[3] = (Lock[3] + move_one) % 4;
				Lock[4] = (Lock[4] + move_one) % 4;

				//修改②相关钟指向
				Lock[0] = (Lock[0] + move_two) % 4;
				Lock[1] = (Lock[1] + move_two) % 4;
				Lock[2] = (Lock[2] + move_two) % 4;

				//修改③相关钟指向
				Lock[1] = (Lock[1] + move_three) % 4;
				Lock[2] = (Lock[2] + move_three) % 4;
				Lock[4] = (Lock[4] + move_three) % 4;
				Lock[5] = (Lock[5] + move_three) % 4;

				//确定④⑤⑥
				int move_four = (4 - Lock[0]) % 4;
				int move_five = (4 - Lock[1]) % 4;
				int move_six = (4 - Lock[2]) % 4;

				//修改④⑤⑥相关钟指向

				Lock[0] = Lock[1] = Lock[2] = 0;

				Lock[3] = (Lock[3] + move_four) % 4;
				Lock[6] = (Lock[6] + move_four) % 4;

				Lock[3] = (Lock[3] + move_five) % 4;
				Lock[4] = (Lock[4] + move_five) % 4;
				Lock[5] = (Lock[5] + move_five) % 4;
				Lock[7] = (Lock[7] + move_five) % 4;

				Lock[5] = (Lock[5] + move_six) % 4;
				Lock[8] = (Lock[8] + move_six) % 4;

				//确定⑦⑨
				int move_seven = (4 - Lock[3]) % 4;
				int move_nine = (4 - Lock[5]) % 4;

				//修改⑦⑨相关钟指向
				Lock[3] = Lock[5] = 0;

				Lock[4] = (Lock[4] + move_seven) % 4;
				Lock[6] = (Lock[6] + move_seven) % 4;
				Lock[7] = (Lock[7] + move_seven) % 4;

				Lock[4] = (Lock[4] + move_nine) % 4;
				Lock[7] = (Lock[7] + move_nine) % 4;
				Lock[8] = (Lock[8] + move_nine) % 4;



				if (Lock[4] != 0)
				{
					continue;
				}
				else
				{
					int temp_one, temp_two, temp_three;
					temp_one = Lock[6];
					temp_two = Lock[7];
					temp_three = Lock[8];

					for (int move_eight = 0; move_eight < 4; move_eight++)
					{
						Lock[6] = (temp_one + move_eight) % 4;
						Lock[7] = (temp_two + move_eight) % 4;
						Lock[8] = (temp_three + move_eight) % 4;

						if (Lock[6] == 0 && Lock[7] == 0 && Lock[8] == 0)
						{
							sum = move_one + move_two + move_three
								+ move_four + move_five + move_six
								+ move_seven + move_eight + move_nine;


							if (sum < Min)
							{
								Min = sum;
								Result[0] = move_one;
								Result[1] = move_two;
								Result[2] = move_three;
								Result[3] = move_four;
								Result[4] = move_five;
								Result[5] = move_six;
								Result[6] = move_seven;
								Result[7] = move_eight;
								Result[8] = move_nine;
							}
						}

					}
				}
			}
		}
	}

	//结果处理
	for (int i = 0; i < 9; i++)
	{
		if (Result[i] != 0)
		{
			for (int j = 0; j < Result[i]; j++)
			{
				v.push_back(i + 1);
			}

		}
	}
	//cout << v.size();
	sort(v.begin(), v.end());
	for (vector<int>::iterator it = v.begin(); it != v.end(); it++)
	{
		cout << * it;
		if (it != v.end() - 1)
		{
			cout << " ";
		}
	}
	cout << endl;
	return 0;
}

#include<iostream>
#include<algorithm>
#include<cstring>
#include<memory>
#include<cmath>
#include<vector>
typedef int Status;
const int OK = 1;
const int ERROR = 0;
using namespace std;
int oriLock[9];
int tmpLock[9];
int tmMoves[9];
int Result[9];
vector<int> vec;
Status oneOperation(int moves)
{
	tmpLock[0] = (tmpLock[0] + moves) % 4;
	tmpLock[1] = (tmpLock[1] + moves) % 4;
	tmpLock[3] = (tmpLock[3] + moves) % 4;
	tmpLock[4] = (tmpLock[4] + moves) % 4;
	return OK;
}

Status twoOperation(int moves)
{
	tmpLock[0] = (tmpLock[0] + moves) % 4;
	tmpLock[1] = (tmpLock[1] + moves) % 4;
	tmpLock[2] = (tmpLock[2] + moves) % 4;
	return OK;
}

Status threeOperation(int moves)
{
	tmpLock[1] = (tmpLock[1] + moves) % 4;
	tmpLock[2] = (tmpLock[2] + moves) % 4;
	tmpLock[4] = (tmpLock[4] + moves) % 4;
	tmpLock[5] = (tmpLock[5] + moves) % 4;
	return OK;
}

Status fourOperation(int moves)
{
	tmpLock[0] = (tmpLock[0] + moves) % 4;
	tmpLock[3] = (tmpLock[3] + moves) % 4;
	tmpLock[6] = (tmpLock[6] + moves) % 4;
	return OK;
}

Status fiveOperation(int moves)
{
	tmpLock[1] = (tmpLock[1] + moves) % 4;
	tmpLock[3] = (tmpLock[3] + moves) % 4;
	tmpLock[4] = (tmpLock[4] + moves) % 4;
	tmpLock[5] = (tmpLock[5] + moves) % 4;
	tmpLock[7] = (tmpLock[7] + moves) % 4;
	return OK;
}

Status sixOperation(int moves)
{
	tmpLock[2] = (tmpLock[2] + moves) % 4;
	tmpLock[5] = (tmpLock[5] + moves) % 4;
	tmpLock[8] = (tmpLock[8] + moves) % 4;
	return OK;
}

Status sevenOperation(int moves)
{
	tmpLock[3] = (tmpLock[3] + moves) % 4;
	tmpLock[4] = (tmpLock[4] + moves) % 4;
	tmpLock[6] = (tmpLock[6] + moves) % 4;
	tmpLock[7] = (tmpLock[7] + moves) % 4;
	return OK;
}

Status eightOperation(int moves)
{
	tmpLock[6] = (tmpLock[6] + moves) % 4;
	tmpLock[7] = (tmpLock[7] + moves) % 4;
	tmpLock[8] = (tmpLock[8] + moves) % 4;
	return OK;
}

Status nineOperation(int moves)
{
	tmpLock[4] = (tmpLock[4] + moves) % 4;
	tmpLock[5] = (tmpLock[5] + moves) % 4;
	tmpLock[7] = (tmpLock[7] + moves) % 4;
	tmpLock[8] = (tmpLock[8] + moves) % 4;
	return OK;
}
int main()
{
	for (int i = 0; i < 9; i++)
	{
		cin >> oriLock[i];
	}
	int Min = 1 << 30;
	for (int one = 0; one < 4; one++)
	{
		for (int two = 0; two < 4; two++)
		{
			for (int three = 0; three < 4; three++)
			{
				int sum = one + two + three;
				memcpy(tmpLock, oriLock, sizeof(oriLock));
				memset(tmMoves, 0, sizeof(tmMoves));
				tmMoves[0] = one;
				tmMoves[1] = two;
				tmMoves[2] = three;
				//第一行局部枚举
				oneOperation(one);
				twoOperation(two);
				threeOperation(three);

				//第二行根据第一行确定
				sum += (4 - tmpLock[0]) % 4;
				tmMoves[3] = (4 - tmpLock[0]) % 4;
				fourOperation((4 - tmpLock[0]) % 4);

				sum += (4 - tmpLock[1]) % 4;
				tmMoves[4] = (4 - tmpLock[1]) % 4;
				fiveOperation((4 - tmpLock[1]) % 4);

				sum += (4 - tmpLock[2]) % 4;
				tmMoves[5] = (4 - tmpLock[2]) % 4;
				sixOperation((4 - tmpLock[2]) % 4);


				//对第二行进行操作，由79决定DF
				sum += (4 - tmpLock[3]) % 4;
				tmMoves[6] = (4 - tmpLock[3]) % 4;
				sevenOperation((4 - tmpLock[3]) % 4);

				sum += (4 - tmpLock[5]) % 4;
				tmMoves[8] = (4 - tmpLock[5]) % 4;
				nineOperation((4 - tmpLock[5]) % 4);
				if (tmpLock[4]!= 0)
				{
					continue;
				}
				else
				{
					int a, b, c;
					a = (4 - tmpLock[6]) % 4;
					b = (4 - tmpLock[7]) % 4;
					c = (4 - tmpLock[8]) % 4;
					if (a == b&&b == c)
					{
						sum += a;
						tmMoves[7]= a;
						if (sum < Min)
						{
							vec.clear();
							for (int i = 0; i < 9; i++)
							{
								if (tmMoves[i] != 0)
								{
									for (int j = 0; j < tmMoves[i]; j++)
									{
										vec.push_back(i + 1);
									}
								}
							}
						}
					}
				}
			}
		}
	}
	for (vector<int>::iterator it = vec.begin(); it != vec.end(); it++)
	{
		cout << *it;
		if (it != vec.end()-1)
		{
			cout << " ";
		}
	}
	cout << endl;
	return 0;
}

第二章递归

递归和普通函数一样通过栈调用。
构成递归需具备的条件：
1.子问题须与原问题为同形式，且更为简单；
2.不能无限制地调用本身，须有个出口，化简为非递归状况出。
递归作用：
a.替代多重循环
b.解决本来就是用递归形式定义的问题
c.将问题分解为规模更小的子问题进行求解

汉诺塔问题

描述
古代有一个梵塔，塔内有三个座A、B、C座上有64个盘子，盘子大小不等，大的在下，小的再上。有一个和尚想把这64个盘子从A座移到C座，但每次只能允许移动一个盘子，并且在移动过程中，3个座上的盘子始终保持大盘在下，小盘在上。在移动过程中可以利用B座，要求输出移动的步骤。
图示
汉诺塔图示
输入
输入为一个整数后面跟三个单字符字符串。
整数为盘子的数目，后三个字符表示三个杆子的编号。
输出
输出每一步移动盘子的记录。一次移动一行。
每次移动的记录为例如3:a->b 的形式，即把编号为3的盘子从a杆移至b杆。
我们约定圆盘从小到大编号为1, 2, …n。即最上面那个最小的圆盘编号为1，最下面最大的圆盘编号为n。
样例输入
3 a b c
样例输出
1:a->c
2:a->b
1:c->b
3:a->c
1:b->a
2:b->c
1:a->c
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：汉诺塔问题.cpp

解题思路：
先将n-1个盘子移动到B座，再将最后一个盘子移动到C座，最后将B上的n-1个盘子移动到C座
具体步骤：
One:假设一个盘子，那么直接从A移动到C即可；
Two:假设有两个盘子，
    那么先将①（A上的从上至下盘子序号递增，从1开始）移到B，这相当于执行One——起始座A，中转座C，目标座B
    随后将②移动到C，相当于执行One——起始座A，中转座B，目标座C
	再将①移到C，相当于执行One——起始座B,中转座A，目标座C
Three:假设有三盘子
    那么重复Two，但是起始座为A，中转座为C，目标座变为B
....
Number_n:假设有n个盘子，同理，调用n-1步骤，递归调用——每次调用思路为，起始座的最后一个盘子调至目标座，而n-1个盘子调至中转座！

当前版本：1.0
作    者：Louris
完成日期：2017.08.05
*/
#include<iostream>
using namespace std;
void Hanoi(int n, char src, char mid, char dest)
{
	/*
	//当只有一个盘子时
	if (n == 1)
	{
		cout << n << ":" << src << "->" << dest << endl;
	return;
	}
	//--承接上述代码，以下代码分类讨论出共性
	//当有两个盘子时
	Hanoi(2 - 1, src, dest, mid);
	cout << 2 << ":" << src << "->" << dest << endl;

	//当有三个盘子时
	Hanoi(3 - 1, src, dest, mid);
	cout << 3 << ":" << src << "->" << dest << endl;
	Hanoi(3 - 1, mid, src, dest);

	//当有四个盘子时
	Hanoi(4 - 1, src, dest, mid);
	cout << 4 << ":" << src << "->" << dest << endl;
	Hanoi(4 - 1, mid, src, dest);
	//...
	//至此规律已出！
	//参见下述代码即可！
	*/


	if (n == 1) //当只有一个盘子时的调用
	{
		cout << n << ":" << src << "->" << dest << endl;
		return;
	}
	Hanoi(n - 1, src, dest, mid);//先将n-1个盘子从src移动到mid

	cout << n << ":" << src << "->" << dest << endl;//再将src中的最后一个盘子从src移动到dest

	Hanoi(n - 1, mid, src, dest);//最后将n-1一个盘子从mid移动到dest
	return;
}
int main()
{
	int n;
	char a, b, c;
	cin >> n>>a>>b>>c;//输入盘子数目
	Hanoi(n, a, b, c);
	return 0;
}

/*
解题思路：
这里计算移动n个盘所需要的最少次数：
①n=1：从src借助mid移动到dst，F[1]=1
②n=2：
	前n-1=1从src借助dst移动到mid，
	第n从src借助mid移动到dst
	前n-1=1从mid借助src移动到dst
	F[2]=2F[1]+1
③n=3：
	前n-1=2从src借助dst移动到mid，
	第n从src借助mid移动到dst
	前n-1=2从mid借助src移动到dst
	F[3]=2F[2]+1
...
n：
	前n-1从src借助dst移动到mid，
	第n从src借助mid移动到dst
	前n-1从mid借助src移动到dst
	F[n]=2F[n-1]+1
故通项公式2^n-1
*/
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
const int MAXN = 64;
vector<int> F;

int main()
{
	int n;
	while (cin >> n)
	{
		F.clear();
		F.push_back(1);
		for (int i = 1; i < n; i++)
		{
			int tmp = 2 * F[i - 1] + 1;
			F.push_back(tmp);
		}
		cout << F[n - 1] << endl;
	}

	return 0;
}

汉诺塔II

Problem Description
经典的汉诺塔问题经常作为一个递归的经典例题存在。可能有人并不知道汉诺塔问题的典故。汉诺塔来源于印度传说的一个故事，上帝创造世界时作了三根金刚石柱子，在一根柱子上从下往上按大小顺序摞着64片黄金圆盘。上帝命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一回只能移动一个圆盘。有预言说，这件事完成时宇宙会在一瞬间闪电式毁灭。也有人相信婆罗门至今仍在一刻不停地搬动着圆盘。恩，当然这个传说并不可信，如今汉诺塔更多的是作为一个玩具存在。Gardon就收到了一个汉诺塔玩具作为生日礼物。
　　Gardon是个怕麻烦的人（恩，就是爱偷懒的人），很显然将64个圆盘逐一搬动直到所有的盘子都到达第三个柱子上很困难，所以Gardon决定作个小弊，他又找来了一根一模一样的柱子，通过这个柱子来更快的把所有的盘子移到第三个柱子上。下面的问题就是：当Gardon在一次游戏中使用了N个盘子时，他需要多少次移动才能把他们都移到第三个柱子上？很显然，在没有第四个柱子时，问题的解是2^N-1，但现在有了这个柱子的帮助，又该是多少呢？
Input
包含多组数据，每个数据一行，是盘子的数目N(1<=N<=64)。
Output
对于每组数据，输出一个数，到达目标需要的最少的移动数。
Sample Input
1
3
12
Sample Output
1
5
81
Procefure

/*
解题思路：
A B C D四个杆儿
先将A上面x个通过BCD移动到B，步数为dp[x]
再把剩下n-x个通过CD移动到C，注意这里不能借助B，因为n-x比B上现存任何盘都要大，pow(2,n-x)-1
最后再把x通过ACD移动到C，此时又是dp[x]
最后移动x至目标盘
即动态规划，
dp[1]=1,dp[2]=3
dp[n]=2*dp[x]+pow(2,n-x)-1
*/
#include<iostream>
#include<algorithm>
#include<cmath>
#include<vector>
using namespace std;
const unsigned long long MAX = 0x3f3f3f3f;
vector<unsigned long long> dp;
int main()
{
	int n;
	while (cin >> n)
	{
		dp.clear();
		dp.push_back(0);
		dp.push_back(1);
		dp.push_back(3);
		for (int i = 3; i <= n; i++)
		{
			dp.push_back(MAX);
			for (int j = 0; j <= i; j++)
			{
				unsigned long long tmp = 2*dp[j] + (unsigned long long)pow(2, i-j) - 1;
				dp[i] = min(dp[i], tmp);
			}
		}
		cout << dp[n] << endl;
	}
	return 0;
}

汉诺塔III

Problem Description
约19世纪末，在欧州的商店中出售一种智力玩具，在一块铜板上有三根杆，最左边的杆上自上而下、由小到大顺序串着由64个圆盘构成的塔。目的是将最左边杆上的盘全部移到右边的杆上，条件是一次只能移动一个盘，且不允许大盘放在小盘的上面。
现在我们改变游戏的玩法，不允许直接从最左(右)边移到最右(左)边(每次移动一定是移到中间杆或从中间移出)，也不允许大盘放到下盘的上面。
Daisy已经做过原来的汉诺塔问题和汉诺塔II，但碰到这个问题时，她想了很久都不能解决，现在请你帮助她。现在有N个圆盘，她至少多少次移动才能把这些圆盘从最左边移到最右边？
Input
包含多组数据，每次输入一个N值(1<=N=35)。
Output
对于每组数据，输出移动最小的次数。
Sample Input
1
3
12
Sample Output
2
26
531440
Procedure

/*
解题思路：
先将n-1盘移至C，需要dp[n-1]
再将最大盘移至B，1
再将n-1盘移至A，需要dp[n-1]
再将最大盘移至C，1
最后n-1盘移至C，需要dp[n-1]
*/
#include<iostream>
#include<algorithm>
#include<cmath>
#include<vector>
using namespace std;
vector<long long> dp;
int main()
{
	int n;
	while (cin >> n)
	{
		dp.clear();
		dp.push_back(0);
		dp.push_back(2);
		for (int i = 2; i <= n; i++)
		{
			long long tmp = 3 * dp[i - 1] + 2;
			dp.push_back(tmp);
		}
		cout << dp[n] << endl;
	}
	return 0;
}

/*
解题思路：
本题会有与其他题目不同的思路，关键在于设的dp[i]
其他是最终结果dp[i]
而本题是i个盘转移至相邻一个盘所需步数dp[i]
那么最终结果是F=2*dp[i]
而dp[i]=3*dp[i-1]+1
*/
#include<iostream>
#include<algorithm>
#include<cmath>
#include<vector>
using namespace std;
vector<long long> dp;

int main()
{
	int n;
	while (cin >> n)
	{
		dp.clear();
		dp.push_back(0);
		for (int i = 1; i <= n; i++)
		{
			long long tmp = 3 * dp[i - 1] + 1;
			dp.push_back(tmp);
		}
		cout << 2 * dp[n] << endl;
	}
	return 0;
}

汉诺塔IV

Problem Description
还记得汉诺塔III吗？他的规则是这样的：不允许直接从最左(右)边移到最右(左)边(每次移动一定是移到中间杆或从中间移出)，也不允许大盘放到小盘的上面。xhd在想如果我们允许最大的盘子放到最上面会怎么样呢？（只允许最大的放在最上面）当然最后需要的结果是盘子从小到大排在最右边。
Input
输入数据的第一行是一个数据T，表示有T组数据。
每组数据有一个正整数n(1 <= n <= 20)，表示有n个盘子。
Output
对于每组输入数据，最少需要的摆放次数。
Sample Input
2
1
10
Sample Output
2
19684
Procedure

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：汉诺塔IV.cpp

总的思路：
i个盘子,
i-1个盘子移动到临近柱子②的次数为a[i-1],(从上到下，从小到大)
然后第i个最大的盘子从①到②再到③走了两次
最后在把i-1个盘子移动到临近柱子③也要a[i-1]次
所以一个盘子总的已从次数为2*a[i-1]+2

那么现在的问题是转到求a[i]上
那么i个盘子，
i-1个从①到②再到③需要2*a[i-1]
第i个移动到②一次，
i-1个从③移动到②a[i-1]次
总共3*a[i-1]+1

a[0]=0
a[1]=1
...
a[i]=3*a[i-1]+1


当前版本：1.0
作    者：Louris
完成日期：2017.11.19
*/
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int a[22]={0,1};
int main(){
    int t,n;
    cin>>t;
    //找规律。。。。。。从最小的开始找
    for(int i=2;i<=20;i++)a[i]=3*a[i-1]+1;
    while(t--){
        scanf("%d",&n);
        //左边到中间 中间移到右边 *2
        cout<<2*a[n-1]+2<<"\n";
    }
    return 0;
}

/*
解题思路：
榆木脑袋真的是
n-1同汉诺塔III，采用移动相邻一根杆儿的递归式
最后移动第n个的时候，相当于2*dp[n-1]+2
*/
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
vector<long long>dp;

int main()
{
	int n;
	int t;
	cin >> t;
	while (t--)
	{
		while (cin >> n)
		{
			dp.clear();
			dp.push_back(0);
			for (int i = 1; i < n; i++)
			{
				dp.push_back(3 * dp[i - 1] + 1);
			}
			dp.push_back(2 * dp[n - 1] + 2);
			cout << dp[n] << endl;
		}
	}
	return 0;
}

n皇后问题

描述
输入整数n，要求n个国际象棋的皇后，摆在n×n的棋盘上，任何两个皇后都不能处于同一条横行、纵行或者斜线上。互相不能攻击，输出全部方案。
输入
输入一个正整数N，则程序输出N皇后的全部摆法。
输出
输出结果里的每一行都代表一种摆法。行里的第i个数字如果是n，就代表第i行的皇后应该放在第n列
皇后的行。列编号都市从1开始计算。
样例输入
4
样例输出
2 4 1 3
3 1 4 2
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：n皇后问题.cpp

解题思路：
由题意可知每行至多一个皇后
①第一行确定皇后
②第二行皇后的位置与第一行的皇后位置比较，不能同列，不能在同一斜线上，确定位置与否
③第三行皇后的位置与第一、二行的皇后位置比较，确定位置与否
...
第n行皇后的位置与前n-1行皇后位置比较，确定位置与否
同在一条斜线，行差等于列差即可判断

当前版本：1.0
作    者：Louris
完成日期：2017.08.05
*/
#include<iostream>
#include<cmath>
using namespace std;
typedef int Status;
#define OK 1
#define ERROR 0
Status NQueen(int N,int k,int QueenPos[])
{
	//计算第k行的皇后位置
	if (k == N)
	{
		for (int i = 0; i < N; i++) //行循环
		{
			cout << QueenPos[i] + 1 << " ";
		}
		cout << endl;
		return OK;
	}
	//逐个判断N个皇后的位置
	for (int i = 0; i < N; i++)//列循环，也相当于第一行皇后位置枚举！！
	{
		int j;
		for (j = 0; j < k; j++) //行循环
		{
			//和已经摆好的k个皇后的位置比较，看是否冲突
			if (QueenPos[j] == i || abs(QueenPos[j] - i) == abs(k - j))
			{
				break; //冲突，测试下一个位置
			}
		}
		if (j == k) //当前选的位置i不冲突
		{
			QueenPos[k] = i; //将第k个皇后摆放在位置i
			NQueen(N, k + 1, QueenPos);
		}
	}
	return ERROR;
}
int main()
{
	int N;
	cin >> N;
	int * QueenPos = new int[N]; //用于存放算好的皇后位置。最左上角是（0,0）

	NQueen(N,0,QueenPos);

	delete[] QueenPos;
	return 0;
}

/*
HDU 2553
*/
#include<iostream>
#include<algorithm>
#include<vector>
#include<cmath>
typedef int Status;
const int OK = 1;
const int ERROR = 0;
using namespace std;
struct Node
{
	int x, y;
	Node(int i, int j) :x(i), y(j) {}
};
vector<Node> vec;
int f[10];
int n;
int sum;
Status Judge(Node i, Node j)
{
	if (i.y == j.y || abs(i.x - j.x) == abs(i.y - j.y))
	{
		return ERROR;
	}
	return OK;
}
Status nQueen(int row)
{
	if (row == n + 1)
	{
		/*for (unsigned int k = 0; k < vec.size(); k++)
		{
			cout << vec[k].y;
			if (k < vec.size() - 1)
			{
				cout << " ";
			}
		}
		cout << endl;*/
		sum++;
		return OK;
	}
	for (int i = 1; i <= n; i++)
	{
		unsigned int j;
		for (j = 0; j < vec.size(); j++)
		{
			if (!Judge(Node(row, i), vec[j]))
			{
				break;
			}
		}
		if (j == vec.size())
		{
			vec.push_back(Node(row, i));
			nQueen(row + 1);
			vec.pop_back();
		}

	}
	return ERROR;
}
int main()
{
	ios::sync_with_stdio(false);
	for (int i = 1; i <= 10; i++)
	{
		n = i;
		sum = 0;
		vec.clear();
		nQueen(1);
		f[i - 1] = sum;
	}
	while (cin >> n&&n!=0)
	{

		cout << f[n-1] << endl;
	}
	return 0;
}

逆波兰表达式

描述
逆波兰表达式是一种把运算符前置的算术表达式，例如普通的表达式2 + 3的逆波兰表示法为+ 2 3。逆波兰表达式的优点是运算符之间不必有优先级关系，也不必用括号改变运算次序，例如（2 + 3） * 4的逆波兰表达法为* + 2 3 4.本题求解逆波兰表达式的值，其中运算符包括+ - * /四个。

输入
输入为一行，其中运算符和运算数之间都有空格分隔开，元算数是浮点数。
输出
输出为一行，表达式的值。
样例输入
* + 11.0 12.0 + 24.0 35.0
样例输出
1357.000000
提示：(11.0+12.0) * (24.0+35.0)

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：逆波兰表达式.cpp

解题思路：
逆波兰表达式的定义：
a.一个数是一个逆波兰表达式，值为该数
b.“运算符 逆波兰表达式 逆波兰表达式”是逆波兰表达式，值为两个逆波兰表达式的值运算的结果

当前版本：1.0
作    者：Louris
完成日期：2017.08.05
*/
#include<iostream>
using namespace std;
double exp()
{
	//读入一个逆波兰表达式，并计算其值
	char s[20];
	cin >> s;
	switch(s[0])
	{
		case '+':return exp() + exp();
		case '-':return exp() - exp();
		case '* ':return exp() * exp();
		case '/':return exp() / exp();
		default:return atof(s);//将一个字符串类型转换成double
	}
}
int main()
{
	printf("%1f", exp());
	return 0;
}

正则表达式(17蓝桥杯)

考虑一种简单的正则表达式：只由 x ( ) | 组成的正则表达式。小明想求出这个正则表达式能接受的最长字符串的长度。
例如 ((xx|xxx)x|(x|xx))xx 能接受的最长字符串是： xxxxxx，长度是6。
输入
一个由x()|组成的正则表达式。输入长度不超过100，保证合法。
输出
这个正则表达式能接受的最长字符串的长度。
例如，
输入：((xx|xxx)x|(x|xx))xx
程序应该输出： 6
资源约定：
峰值内存消耗（含虚拟机）< 256M CPU消耗< 1000ms
请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。注意： main函数需要返回0; 只使用ANSI C/ANSI C++ 标准; 不要调用依赖于编译环境或操作系统的特殊函数。所有依赖的函数必须明确地在源文件中 #include
不能通过工程设置而省略常用头文件。提交程序时，注意选择所期望的语言类型和编译器类型。

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int factor_value();
int term_value();
int expression_value();
int expression_value()
{
	int result=term_value();
	while(true)
	{
		char op=cin.peek();
		if(op=='|')
		{
			cin.get();
			int value=term_value();
			result=max(result,value);
		}
		else
		{
			break;
		}
	}
	return result;
}

int term_value()
{
	int result=0;

	char op=cin.peek();
	if(op=='(')
	{
		cin.get();
		result=expression_value();
		cin.get();
		op=cin.peek();
		if(op=='x')
		{
			result+=factor_value();
		}
	}
	else if(op=='x')
	{
		result=factor_value();
	}
	return result;
}

int factor_value()
{
	int result=0;
	char op=cin.peek();
	while(op=='x')
	{
		result++;
		cin.get();
		op=cin.peek();
	}
	if(op=='(')
	{
		result+=term_value();
	}
	return result;
}
int main()
{
	cout<<expression_value()<<endl;
	return 0;
}

表达式求值

描述
输入为四则运算表达式，仅由数字、+、-、*、/、（、）组成，没有空格，要求求其值。假设运算符结果都是整数。“/”结果也是整数。
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：表达式求值.cpp

解题思路：
递归形式的定义：
按运算符优先级递增顺序进行排列：
表达式：项 “+” 或 “-” 项
项：因子 “*”或 “/” 因子
因子：“(表达式)”或 整数
因此对于表达式可以采用递归

当前版本：1.0
作    者：Louris
完成日期：2017.08.06
*/
#include<iostream>
#include<cctype>
using namespace std;
int expression_value();
int term_value();
int factor_value();

int expression_value() //求一个表达式的值
{
	int result = term_value(); //求第一项的值
	while (true)
	{
		char op = cin.peek(); //看一个字符，不取走
		if (op == '+' || op == '-')
		{
			cin.get(); //从输入中取走一个字符
			int value = term_value();
			if (op == '+')
			{
				result += value;
			}
			else
			{
				result -= value;
			}
		}
		else
		{
			break;
		}
	}
	return result;
}

int term_value() //求一个项的值
{
	int result = factor_value(); //求第一个因子的值
	while (true)
	{
		char op = cin.peek();
		if (op == '*' || op == '/')
		{
			cin.get();
			int value = factor_value();
			if (op == '*')
			{
				result *= value;
			}
			else
			{
				result /= value;
			}
		}
		else
		{
			break;
		}
	}
	return result;
}

int factor_value()
{
	int result = 0;
	char c = cin.peek();
	if (c == '(')
	{
		cin.get(); //处理(
		result = expression_value();
		cin.get(); //处理)
	}
	else
	{
		while (isdigit(c))
		{
			result = 10 * result + c - '0';
			cin.get();//去掉
			c = cin.peek();//只读
		}
	}
	return result;
}

int main()
{
	cout << expression_value() << endl;
	return 0;
}

上台阶

描述
树老师爬楼梯，他可以每次走1级或者2级，输入楼梯的级数，求不同的走法数。
输入
包含若干行，每行包含一个正整数N，代表楼梯级数，1<=N<=30
输出
输出不同的走法数，每一行输入对应一行
样例输入
5
8
10
样例输出
8
34
89
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：上台阶.cpp

解题思路：

n级台阶的走法=
先走一级后，n-1级台阶的走法 +
先走两级后，n-2级台阶的走法
f(n)=f(n-1)+f(n-2)

边界条件：
以下三者之一
n<0 0
n=0 1

n=0 1
n=1 1

n=1 1
n=2 2

当前版本：1.0
作    者：Louris
完成日期：2017.08.06
*/

#include<iostream>
using namespace std;
int Stairs(int n)
{
	if (n == 0)
	{
		return 1;
	}
	else if (n == 1)
	{
		return 1;
	}
	else
	{
		return Stairs(n - 1) + Stairs(n - 2);
	}
}
int main()
{
	int N;
	while (cin >> N)
	{
		cout << Stairs(N) << endl;
	}
	return 0;
}

#include<iostream>
#include<algorithm>
#include<string>
#include<cctype>
#include<vector>
using namespace std;
vector<int> vec;
int main()
{
	int n;
	while(cin>>n)
	{
		vec.clear();
		vec.push_back(0);
		vec.push_back(1);
		vec.push_back(2);
		for(int i=3;i<=n;i++)
		{
			vec.push_back(vec[i-1]+vec[i-2]);
		}
		cout<<vec[n]<<endl;
	}
	return 0;
}

放苹果

把M个同样的苹果放在N个同样的盘子里，允许有的盘子空着不方，问共有多少种不同的分法？5,1,1和1,5,1是同一种分法。
输入
第一行是测试数据的数目t(0<=t<=20)。以下每行均包含两个整数M和N，以空格分开。1<=M,N<=10。
输出
对输入的每组数据M和N，用一行输出相应的K。
样例输入
1
7 3
样例输出
8
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：放苹果.cpp

解题思路：
设i个苹果放在k个盘子里方法总数是f(i,k)，则：
k > i 时， f(i,k) = f(i,i)
k <= i 时，总放法=有盘子为空的方法+没盘子为空的方法
f(i,k)=f(i,k-1)+f(i-k,k)

临界条件：
i=0 f=1
i!=0 k=0 f=0

当前版本：1.0
作    者：Louris
完成日期：2017.08.06
*/

#include<iostream>
using namespace std;
int Put_apples(int m, int n)
{
	if (m < n)
	{
		return Put_apples(m, m);
	}
	else if (m == 0)
	{
		return 1;
	}
	else if (n == 0)
	{
		return 0;
	}
	else
	{
		return Put_apples(m, n - 1) + Put_apples(m - n, n);
	}
}

int main()
{
	int t, m, n;
	cin >> t;
	while (t--)
	{
		cin >> m >> n;
		cout << Put_apples(m, n) << endl;
	}
	return 0;
}

算24

描述
给出4个小于10个正整数，你可以使用加减乘除4种运算以及括号把这4个数连接起来得到一个表达式。现在的问题是，是否存在一种方式使得得到的表达式的结果等于24.
输入
输入数据包括多行，每行给出一组测试数据，包括4个小于10个正整数。最后一组测试数据中包括4个0，表示输入的结束，这组数据不用处理。
输出
对于每一组测试数据，输出一行，如果可以得到24，输出“YES”；
否则，输出“NO”；
样例输入
5 5 5 1
1 1 4 2
0 0 0 0
样例输出
YES
NO
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：算24.cpp

解题思路：
外层总的递归思路：
n个数算24，必有两个数要先算。
这两个数算的结果，和剩余n-2个数，就构成了n-1个数求24的问题。
枚举先算的两个数，以及这两个数的运算方式。
边界条件：
 一个数算24

 注意：浮点数比较是否相等，不能用 ==
 两个浮点数之差小于某个很小的值判断

 内层策略：
 n个数组合有C(2，n) = n * (n - 1) / 2种
 进行加减乘除模拟，若有一个成立则YES，否则NO


当前版本：1.0
作    者：Louris
完成日期：2017.08.06
*/

#include<iostream>
#include<cmath>
using namespace std;
const int Num = 4;
const double EPS = 1e-6;
bool IsZero(double x)
{
	return fabs(x) <= EPS;
}

bool Count_24(double Data[], int n)
{
	//用数组里的n个数，计算24
	if (n == 1)
	{
		if (IsZero(Data[0] - 24))
		{
			return true;
		}
		else
		{
			return false;
		}
	}
	else
	{
		double temp[Num];
		for (int i = 0; i < n - 1; i++)
		{
			for (int j = i + 1; j < n; j++) //枚举两个数的组合
			{
				int m = 0; //还剩下m个数，m = n-2
				for (int k = 0; k < n; k++)
				{
					if (k != i&&k != j)
					{
						temp[m++] = Data[k]; //把其余数放入b
					}
				}

				//加法
				temp[m] = Data[i] + Data[j];
				if (Count_24(temp, m + 1))
				{
					return true;
				}

				//减法
				temp[m] = Data[i] - Data[j];
				if (Count_24(temp, m + 1))
				{
					return true;
				}
				temp[m] = Data[j] - Data[i];
				if (Count_24(temp, m + 1))
				{
					return true;
				}
				//乘法
				temp[m] = Data[i] * Data[j];
				if (Count_24(temp, m + 1))
				{
					return true;
				}

				//除法
				if (!IsZero(Data[j]))
				{
					temp[m] = Data[i] / Data[j];
					if (Count_24(temp, m + 1))
					{
						return true;
					}
				}
				if (!IsZero(Data[j]))
				{
					temp[m] = Data[j] / Data[i];
					if (Count_24(temp, m + 1))
					{
						return true;
					}
				}
			}
		}
		return false;
	}

}

int main()
{
	double Data[Num];
	while (true)
	{
		int flag = 0;
		for (int i = 0; i < Num; i++)
		{
			cin >> Data[i];
			if (Data[i] == 0)
			{
				flag++;
			}
		}
		if (flag == Num)
		{
			break;
		}
		if (Count_24(Data, Num))
		{
			cout << "YES" << endl;
		}
		else
		{
			cout << "NO" << endl;
		}
	}
	return 0;
}

全排列

描述
给定一个由不同的小写子组成的字符串，输出这个字符串的所有全排列。我们假设对于小写字母有’a’<’b’<…<’y’<’z’，而且给定字符串中的字母已经按照从小到大的顺序排列。
输入
输入只有一行，是一个由不同的小写字母组成的字符串，已知字符串的长度在1到6之间。
输出
输出这个字符串的所有排列方式，每行一个排列。要求字母序比较小的排列在前面。字母序如下定义：

已知S = s1s2…sk , T = t1t2…tk，则S < T 等价于，存在p (1 <= p <= k)，使得
s1 = t1, s2 = t2, …, sp - 1 = tp - 1, sp < tp成立。
样例输入
abc
样例输出
abc
acb
bac
bca
cab
cba
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：全排列.cpp

解题思路：
由于给定的字符串已经是小写字母组成的字母序，所以：
设该字符串由n个字符组成，设排列总数为Alphabets(str,n)：
①循环取字符串的每个字符，那么以该字符为首的排列组合总数为剩下字符的全排列：
Alphabets(str,n) = Alphabets(str_new,n-1);
重复调用即可。

边界条件：
n=0

Accepted：
deque双端队列：2ms
string字符串：1ms

当前版本：1.0
作    者：Louris
完成日期：2017.08.07
*/
#include<iostream>
#include<string>
#include<deque>
using namespace std;


void Alphabets(string str,/*deque<char>*/string Result)
{
	if (str.length() == 0)
	{
		/*for (deque<char>::iterator it = Result.begin(); it != Result.end(); it++)
		{
			cout << *it;
		}*/
		for (string::iterator it = Result.begin(); it != Result.end(); it++)
		{
			cout << *it;
		}
		cout << endl;
	}
	else
	{
		string temp = str;
		for (unsigned int i = 0; i < temp.length(); i++)
		{
			str = temp;
			//Result.push_back(str[i]);
			Result += str[i];
			str.erase(str.find(str[i]),1); //剔除当前已加入Result的字符
			Alphabets(str,Result);
			/*if (Result.size() != 0)
			{
				Result.pop_back();
			}*/
			if (Result.length() != 0)
			{
				Result.erase(Result.end()-1);
			}
		}
	}
}

int main()
{
	string Str;
	//deque<char> Result;
	string Result;
	cin >> Str;
	Alphabets(Str,Result);
	return 0;
}

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
string str;

typedef int Status;
const int OK=1;
const int ERROR=0;
Status Alphabets(string ss,string result)
{
	if(str.length()==result.length())
	{
		cout<<result<<endl;
		return OK;
	}
	string temp=ss;
	for(int i=0;i<temp.length();i++)
	{
		ss=temp;
		result+=ss[i];
		ss.erase(ss.find(temp[i]),1);
		Alphabets(ss,result);
		result.erase(result.length()-1,1);
	}
}
int main()
{
	cin>>str;
	string result;
	Alphabets(str,result);
	return 0;
}

2的幂次方表示

描述
任何一个正整数都可以用2的幂次方表示。
例如：
137=2(7)+2(3)+2(0)
同时约定方次用括号来表示，即ab可表示为a(b)。由此可知，137可表示为：
2(7)+2(3)+2(0)
进一步：
7=2(2)+2+2(0)（2(1)用2表示）
3=2+2(0)
所以最后137可表示为：
2(2(2)+2+2(0))+2(2+2(0))+2(0)
又如：
1315=210+28+25+2+1
所以1315最后可表示为：
2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)
输入
一个正整数n(n<=20000)。
输出
一行，符合约定的n的0,2表示（在表示中不能有空格）。
样例输入
137
样例输出
2(2(2)+2+2(0))+2(2+2(0))+2(0)
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：2的幂次方表示.cpp

解题思路：
例如：
137=2(7)+2(3)+2(0)
7=2(2)+2+2(0)
3=2+2(0)

递归
边界条件
number=0或1或2

当前版本：1.0
作    者：Louris
完成日期：2017.08.08
*/
#include<iostream>
#include<cmath>
using namespace std;
typedef int Status;
#define OK 1
#define ERROR 0

Status Calculate(int n)
{
	bool first = true;
	for (int i = 15; i >= 0; i--)
	{
		if (pow(2, i) <= n)
		{
			if (!first)
			{
				cout << "+";
			}
			else
			{
				first = false;
			}
			if (i == 0)
			{
				cout << "2(0)";
			}
			else if (i == 1)
			{
				cout << "2";
			}
			else
			{
				cout << "2(";
				Calculate(i);
				cout << ")";
			}
			n -= (int)pow(2, i);
		}

	}
	return OK;
}

int main()
{
	int n;
	cin >> n;
	Calculate(n);
	return 0;
}

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：2的幂次方表示_改进版.cpp

解题思路：
例如：
137=2(7)+2(3)+2(0)
7=2(2)+2+2(0)
3=2+2(0)

递归
边界条件
number=0或1或2

特点！！！
2的幂次可以考虑二进制！！！现成！！！！
刚开始怎么没想到，看来还是没有习惯用二进制的思路啊！！！
慢慢来！

当前版本：1.0
作    者：Louris
完成日期：2017.08.08
*/

#include<iostream>
using namespace std;
typedef int Status;
#define OK 1
#define ERROR 0

inline int GetBit(int n, int i)
{
	return (n >> i) & 1;
}

Status Print(int n)
{
	bool first = true;
	for (int i = 15; i >= 0; --i)
	{
		if (GetBit(n, i) != 0)
		{
			if (!first)
			{
				cout << "+";
			}
			else
			{
				first = false;
			}
			if (i == 0)
			{
				cout << "2(0)";
			}
			else if(i==1)
			{
				cout << "2";
			}
			else
			{
				cout << "2(";
				Print(i);
				cout << ")";
			}
		}
	}
	return OK;
}

int main()
{
	int n;
	cin >> n;
	Print(n);
	return 0;
}

简单的整数划分问题

描述
将正整数n 表示成一系列正整数之和，n=n1+n2+…+nk, 其中n1>=n2>=…>=nk>=1 ，k>=1 。
正整数n 的这种表示称为正整数n 的划分。正整数n 的不同的划分个数称为正整数n 的划分数。
输入
标准的输入包含若干组测试数据。每组测试数据是一个整数N(0 < N <= 50)。
输出
对于每组测试数据，输出N的划分数。
样例输入
5
样例输出
7
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：简单整数划分问题.cpp

解题思路：
和放苹果思路相当！！！！突然发现！！百度了下的解释！
傻了！排列组合！

所谓整数划分，是指把一个正整数n写成
n=m1+m2+...+mi
其中，mi为正整数，并且1<=mi<=n;{m1,m2,...,mi}为n的一个划分。
如果{m1,m2,...,mi}中的最大值不超过m，即max{m1,m2,...mi}<=m，则称它属于n的一个m划分

这里我们记n的m划分的个数为f(n,m)
例如，当n=4时，有5个划分，即
4,3+1,2+2,2+1+1,1+1+1+1
注意：4=3+1和4=1+3被认为是同一个划分。

根据n和m的关系，考虑一下几种情况：
（一）当n=0时，1种划分,空划分，详见代码，假设n=2,m=2则1+1 有f(2,2)=f(0,2)+f(2,1),所以f(0,2)=1
（二）当m=1时，无论n(正整数，非零)的值为多少，只有一种划分，即 n个1，{1,1,1...1}
（三）当n<m时，由于划分中不可能出现负数，因此就相当于f(n,n)
（四）当n>=m时，以分为以下两种情况：
n的m划分=m划分皆非空+m划分中有一个划分为空
 f(n,m)=f(n-m,m)+f(n,m-1)

当前版本：1.0
作    者：Louris
完成日期：2017.08.08
*/

#include<iostream>
using namespace std;
typedef int Status;
#define OK 1
#define ERROR 0

Status Integer_partition(int n,int m)
{
	if (n == 0)
	{
		return 1;
	}
	else if (m == 1)
	{
		return 1;
	}
	else if(n<m)
	{
		return Integer_partition(n, n);
	}
	else
	{
		return Integer_partition(n - m, m) + Integer_partition(n, m - 1);
	}
	return OK;
}

int main()
{
	int n;
	while (cin >> n)
	{
		cout << Integer_partition(n,n) << endl;
	}
	return 0;
}

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：简单整数划分问题之模式输出.cpp

解题思路：

一、初步思路：
之前的程序是求总数
那么本程序为了输出模式
例如：
n=5
5,4+1,3+2,3+1+1,2+2+1,2+1+1+1,1+1+1+1+1

那么后一个数必须不大于前一个数
①关于n枚举，i=n~1
②关于n-i枚举，并且n-i<i
③重复②

边界条件：
n-i=0

二、改进思路
有一个问题需要解决，就是在前一个数确定的情况下，之后有多种结果的输出
那么在存储前一个数的情况下，每输出其可能的一种情况，检查是否还有其他可能：
如果有，则清空上一种结果中前一个数之后的所有数；
如果没有，则清空上一种结果中前一个数及其之后的所有数。
那么为了方便存储和删除，拟采用双端队列容器deque
具体步骤如下：
设整数n，双端队列容器deque<int> Integer_Model
①对n进行枚举,i=n~1,Integer_Model.push_back(i);
②对n-i进行枚举，i_new=n-i~1,并且i_new <= i（后一个数小于前一个数），Integer_Model.push_back(i_new);
③重复②，直至n-i为0，输出Integer_Model，

关键步骤在于返回跳转后的删除前一个数即可
详见代码

当前版本：1.0
作    者：Louris
完成日期：2017.08.09
*/

#include<iostream>
#include<deque>
using namespace std;
typedef int Status;
#define OK 1
#define ERROR 0
deque<int> Integer_Model;

Status Model(int n, int k)
{
	if (n == 0)
	{
		for (deque<int>::iterator it = Integer_Model.begin(); it != Integer_Model.end(); it++)
		{
			if (it != Integer_Model.begin())
			{
				cout << "+";
			}
			cout << *it;
		}
		cout << endl;
	}
	else
	{
		for (int i = n; i >= 1; i--) //刚开始把i<=k放在两个分号里了，简直煞笔！！妈的，又找了半天，调试了还说什么鬼，蠢了！
		{
			if (i <= k)
			{
				Integer_Model.push_back(i); //进队列
				Model(n - i, i);
				Integer_Model.pop_back(); //出队列
			}
		}
	}
	return OK;
}

int main()
{
	int n;
	cin >> n;
	Model(n, n);
	return 0;
}

Boolean Expressions

描述
The objective of the program you are going to produce is to evaluate boolean expressions as the one shown next:
Expression: ( V | V ) & F & ( F | V )

where V is for True, and F is for False. The expressions may include the following operators: ! for not , & for and, | for or , the use of parenthesis for operations grouping is also allowed.

To perform the evaluation of an expression, it will be considered the priority of the operators, the not having the highest, and the or the lowest. The program must yield V or F , as the result for each expression in the input file.
输入
The expressions are of a variable length, although will never exceed 100 symbols. Symbols may be separated by any number of spaces or no spaces at all, therefore, the total length of an expression, as a number of characters, is unknown.

The number of expressions in the input file is variable and will never be greater than 20. Each expression is presented in a new line, as shown below.
输出
For each test expression, print “Expression “ followed by its sequence number, “: “, and the resulting value of the corresponding test expression. Separate the output for consecutive test expressions with a new line.

Use the same format as that shown in the sample output shown below.
样例输入
( V | V ) & F & ( F| V)
!V | V & V & !F & (F | V ) & (!F | F | !V & V)
(F&F|V|!V&!F&!(F|F&V))
样例输出
Expression 1: F
Expression 2: V
Expression 3: V
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：Boolean_Expressions.cpp

解题思路：
按操作符优先级增序组成下列各式：
表达式：项 | 项 循环
项：因子 & 因子 循环
因子：“（表达式）”
	  或者 V
	  或者 F
	  或者 !V
	  或者 !F
	  或者 !(表达式)——!因子

注意：此版本能够得出正确答案，无奈main函数采用死循环，无法AC

当前版本：1.0
作    者：Louris
完成日期：2017.08.08
*/

#include<iostream>
using namespace std;

bool expression_value();
bool term_value();
bool factor_value();

bool expression_value()
{
	bool result = term_value();
	while (true)
	{
		char op = cin.peek();
		while (op == ' ')
		{
			cin.get();
			op = cin.peek();
		}

		if (op == '|')
		{
			cin.get();
			bool value = term_value();
			result = result || value;
		}
		else
		{
			break;
		}
	}
	return result;
}

bool term_value()
{
	bool result = factor_value();
	while (true)
	{
		char op = cin.peek();
		while (op == ' ')
		{
			cin.get();
			op = cin.peek();
		}

		if (op == '&')
		{
			cin.get();
			result &= factor_value();
		}
		else
		{
			break;
		}
	}
	return result;
}

bool factor_value()
{
	bool result;
	char c = cin.peek();
	while (c == ' ')
	{
		cin.get();
		c = cin.peek();
	}
	if (c == '(')
	{
		cin.get();
		result = expression_value();
		cin.get();
	}
	else if (c == '!')
	{
		cin.get();
		result = !factor_value();
	}
	else
	{
		if (c == 'V')
		{
			result = true;
		}
		else
		{
			result = false;
		}
		cin.get();
	}
	return result;
}

int main()
{
	int i = 1;
	while (true)
	{
		if (expression_value() == true)
		{
			cout << "Expression " << i++ << ": V" << endl;
		}
		else
		{
			cout << "Expression " << i++ << ": F" << endl;
		}
		cin.get(); //peek居然获取回车
	}

	return 0;
}

/*
Copyright(c)2017, Louris
All rights reserved.
文件名称：Boolean_Expressions_AC改进版.cpp
解题思路：
按操作符优先级降序组成下列各式：
表达式：项 | 项 循环
项：因子 & 因子 循环
因子：“（表达式）”
或者 V
或者 F
或者 !V
或者 !F
或者 !(表达式)——!因子

替代版本：Boolean_Expressions.cpp
替代理由：为了AC必须控制循环输入这个条件，那么采用中间string类变量存储输入流

当前版本：1.0
作    者：Louris
完成日期：2017.08.08
*/

#include<iostream>
#include<string>
using namespace std;

bool expression_value();
bool term_value();
bool factor_value();

string str;

bool expression_value()
{
	bool result = term_value();
	while (true)
	{
		//char op = cin.peek();
		char op = str[0];
		while (op == ' ')
		{
			/*cin.get();
			op = cin.peek();*/
			str.erase(str.begin());
			op = str[0];
		}

		if (op == '|')
		{
			//cin.get();
			str.erase(str.begin());
			bool value = term_value();
			result = result || value;
		}
		else
		{
			break;
		}
	}
	return result;
}

bool term_value()
{
	bool result = factor_value();
	while (true)
	{
		//char op = cin.peek();
		char op = str[0];
		while (op == ' ')
		{
			/*cin.get();
			op = cin.peek();*/
			str.erase(str.begin());
			op = str[0];
		}

		if (op == '&')
		{
			//cin.get();
			str.erase(str.begin());
			result &= factor_value();
		}
		else
		{
			break;
		}
	}
	return result;
}

bool factor_value()
{
	bool result;
	//char c = cin.peek();
	char c = str[0];
	while (c == ' ')
	{
		/*cin.get();
		c = cin.peek();*/
		str.erase(str.begin());
		c = str[0];
	}
	if (c == '(')
	{
		//cin.get();
		str.erase(str.begin());
		result = expression_value();
		//cin.get();
		str.erase(str.begin());
	}
	else if (c == '!')
	{
		//cin.get();
		str.erase(str.begin());
		result = !factor_value();
	}
	else
	{
		if (c == 'V')
		{
			result = true;
		}
		else
		{
			result = false;
		}
		//cin.get();
		str.erase(str.begin());
	}
	return result;
}

int main()
{
	int i = 1;
	while (getline(cin,str))
	{
		if (expression_value() == true)
		{
			cout << "Expression " << i++ << ": V" << endl;
		}
		else
		{
			cout << "Expression " << i++ << ": F" << endl;
		}
	}

	return 0;
}

第三章分治

基本概念

把一个任务，分成形式和原任务相同，但规模更小的几个部分任务（通常是两个部分），分别完成，或只需要选一部分完成。然后再处理完成后的这一个或几个部分的结果，实现整个任务的完成。

分治的生活实例——称假币

16硬币，有可能有1枚假币，假币比真币轻。有一架天平，用最少称量次数确定有没有假币，若有的话，假币是哪一枚。
8 - 8 一称，发现无假币，或假币所在的那8枚
4 - 4 一称
2 - 2 一称
1 - 1 一称

分治的典型应用：归并排序

数组排序任务可以如下完成：
①把前一半排序
②把后一半排序
③把两半归并到一个新的有序数组，然后再拷贝回原数组，排序完成。

时间复杂度
时间复杂度：
$T\left(n\right)$
$=2,T\left(\frac{n}{2}\right) + a,n$
$= 2,\left(2,T\left(\frac{n}{4}\right) + a,\frac{n}{2}\right) + a,n$
$= 4,T\left(\frac{n}{4}\right) + 2,a,n$
$= 4,\left(2,T\left(\frac{n}{8}\right) + a,\frac{n}{4}\right) + 2,a,n$
$= 8,T\left(\frac{n}{8}\right) + 3,a,n$
$…$
$= 2^k,T\left(\frac{n}{2^k}\right) + k,a,n$

一直做到 $\frac{n}{2^k}=1$（此时$k=\log_2 n$),
$T\left(n\right)$
$= 2^k,T\left(1\right) + k,a,n$
$=2^k,T\left(1\right) + k,a,n$
$=2^k + k,a,n$
$=n + a,n,\log_2 n$

复杂度$O\left(n\log n\right)$

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：归并排序.cpp

解题思路：
数组排序任务可以如下完成：
①把前一半排序
②把后一半排序
③把两半归并到一个新的有序数组，然后再拷贝回原数组，排序完成。

时间复杂度：
两步归并，再加最后的合并，合并时间复杂度T(n)=O(n) 关于n成正比故a*n,a是常数
T(n) = 2 * T(n / 2) + a*n
= 2 * (2 * T(n / 4) + a*n / 2) + a*n
= 4 * T(n / 4) + 2 * a*n
= 4 * (2 * T(n / 8) + a*n / 4) + 2 * a*n
= 8 * T(n / 8) + 3 * a*n
...
= 2 ^ k*t(n / 2 ^ k) + k*a*n

一直做到 n/2^k=1（此时k=log2(n)),
T(n) = 2^k * T(1) + k * a * n
=2^k * T(1) + k * a * n
=2^k + k * a * n
=n + a * n * log2(n)
复杂度O(nlog n)

当前版本：1.0
作    者：Louris
完成日期：2017.08.09
*/

#include<iostream>
using namespace std;
typedef int Status;
#define OK 1
#define ERROR 0

Status Merge(int a[], int s, int m, int e, int temp[])
{
	//将数组a的局部a[s,m]和a[m+1,e]合并到temp，并保证temp有序，然后再拷贝回a[s,m】
	//归并操作时间复杂度：O(e-m+1)
	int pb = 0;
	int p1 = s, p2 = m + 1;
	while (p1 <= m&&p2 <= e)
	{
		if (a[p1] < a[p2])
		{
			temp[pb++] = a[p1++];
		}
		else
		{
			temp[pb++] = a[p2++];
		}
	}
	while (p1 <= m)
	{
		temp[pb++] = a[p1++];
	}
	while (p2 <= e)
	{
		temp[pb++] = a[p2++];
	}
	for (int i = 0; i < e - s + 1; i++)
	{
		a[s + i] = temp[i];
	}
	return OK;
}

Status MergeSort(int a[], int s, int e, int temp[])
{
	if (s < e)
	{
		//int m = s + (e - s) / 2;
		int m = (s + e) / 2;
		MergeSort(a, s, m, temp);
		MergeSort(a, m + 1, e, temp);
		Merge(a, s, m, e, temp);
	}
	return OK;
}



int main()
{
	int a[10] = { 13,27,19,2,8,12,2,8,30,89 };
	int b[10];
	int size = sizeof(a) / sizeof(int);
	MergeSort(a, 0, size - 1, b);
	for (int i = 0; i < size; ++i)
	{
    cout << a[i];
		if (i != size - 1)
		{
			cout << ",";
		}
	}
	cout << endl;

	return 0;
}

分治的典型应用：快速排序

算法思想：
　　　　一次快排：每次high从高位向前找到第一个比枢纽记录小的记录，交换low和high两记录，之后low从低位向高位找到第一个比枢纽记录大的记录，交换low和high两记录，直至最后high与low相等为止，完成一次快排，所得结果，枢纽左边的数都比它小，枢纽右边的数都比它大。
　　　　采用递归，对枢纽两边的序列二分，分两部分再次进行一次快排，以此类推，直至low与high相等

代码：

int Partition(SqList &L,int low,int high) {
	//一次快排
	//int low = 1, high = L.length;
	//KeyType pivotkey = L.r[low].key;
	while (low < high) {
		while (low < high&&L.r[high].key >=/*pivotkey*/ L.r[low].key) --high;
		swap(L.r[low], L.r[high]);
		while (low < high&&L.r[low].key <=/*pivotkey*/ L.r[high].key) ++low;
		swap(L.r[low], L.r[high]);
	}
	return low;
}
Status QSort(SqList &L,int low,int high) {
　//快速排序
　//int low = 1, high = L.length;
　if (low < high) {
　　int pivotloc = Partition(L, low, high);
　　　QSort(L, low, pivotloc - 1);
　　　QSort(L, pivotloc + 1, high);
	}
　return OK;
}

求排列的逆序对数

考虑1,2,…,n(n<=100000)的排列i1,i2,…,in,如果其中存在j,k，满足j<k且ij>ik，那么就称(ij,ik)是这个排列的一个逆序。
先给顶1,2,…,n的一个排列，求它的逆序数。

笨办法：O(n^2)

分治：O(nlogn)
①将数组分成两半，分别求出左半边的逆序数和右半边的逆序数
②再算有多少逆序是由左半边取一个数和右半边取一个数构成（要求O(n)）实现。

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：逆序对数.cpp

解题思路：
笨办法：O(n^2)

分治：O(nlogn)
①将数组分成两半，分别求出左半边的逆序数和右半边的逆序数
②再算有多少逆序是由左半边取一个数和右半边取一个数构成（要求O(n)）实现。
③重复上述两步即可，会发现最终停留在两个数的合并的②中，所以只要计算每次分治②中的逆序对数并累加即可！！（分析半天就一句话，无奈！）
关键在于：左半边和右半边都是排好序的。比如，都是从大到小排序的。
这样，左右半边只需要从头到尾各扫一遍，就可以找出由两边各取一个数构成逆序对个数。

降序排列：
10 8 7 3 | 12 11 5 2
i          j           左边剩余所有数都不成立
i             j        左边剩余所有数都不成立
i                j     右边剩余所有数都成立
   i             j     右边剩余所有数都成立
     i           j     右边剩余所有数都成立
	   i         j     左边剩余所有数都不成立
	   i           j   右边剩余所有数都成立
左边第i个数与右边第j个数比较：
若左边比右边大，则说明左边当前最大值都比左边当前最大值大，即右边剩余所有数都是满足的，计算右边剩余数的个数即可
若左边比右边小或等于，则说明左边当前最大值都比右边当前最大值小，即左边剩余所有数都是不满足的

升序排列：
3 7 8 10 | 2 5 11 15
i          j            左边剩余所有数都成立
i            j          右边剩余所有数都不成立
  i          j          左边剩余所有数都成立
  i            j        右边剩余所有数都不成立
    i          j        右边剩余所有数都不成立
	  i        j        右边剩余所有数都不成立
左边第i个数与右边第j个数比较：
若左边比右边大，则说明左边当前最小值都比右边当前最小值大，即左边剩余所有数都是满足的，计算左边剩余数的个数即可
若左边比右边小或等于，则说明左边当前最小值都比右边当前最小值小或等于，即右边剩余所有数都是不满足的

对应AC题网址：（注意限制，数组元素过大，逆序对计数定义为long long型即可
https://acm.sjtu.edu.cn/OnlineJudge/problem/1572

当前版本：1.0
作    者：Louris
完成日期：2017.08.09
*/

#include<iostream>
#include<vector>
#include<vector>
using namespace std;
typedef int Status;
#define OK 1
#define ERROR 0

long long Count_Inversion_pair = 0;
Status Merge(vector<int> &a, int low, int mid, int high, int temp[])
{
	//将数组a的局部a[low,mid]和a[mid+1,high]合并到temp，并保证temp有序，然后再拷贝回a[low,mid]
	//归并操作时间复杂度：O(high-mid+1)
	int pb = 0;
	int p1 = low, p2 = mid + 1;
	while (p1 <= mid&&p2 <= high)
	{
		if (a[p1] <= a[p2])
		{
			temp[pb++] = a[p1++];
		}
		else
		{
			Count_Inversion_pair += mid - p1 + 1;

			temp[pb++] = a[p2++];
		}
	}
	while (p1 <= mid)
	{
		temp[pb++] = a[p1++];
	}
	while (p2 <= high)
	{
		temp[pb++] = a[p2++];
	}
	for (int i = 0; i < high - low + 1; i++)
	{
		a[low + i] = temp[i];
	}
	return OK;
}

Status MergeSort(vector<int> &a, int low, int high, int temp[])
{
	if (low < high)
	{
		//int m = low + (high - low) / 2;
		int m = (low + high) / 2;
		MergeSort(a, low, m, temp);
		MergeSort(a, m + 1, high, temp);
		Merge(a, low, m, high, temp);
	}
	return OK;
}
int main()
{
	vector<int> a;
	int n;
	while (cin >> n)
	{

		for (int i = 0; i < n; i++)
		{
			int x;
			cin >> x;
			a.push_back(x);
		}
		int *b = new int[n];
		MergeSort(a, 0, a.size() - 1, b);
		cout << Count_Inversion_pair << endl;
		a.clear();
		delete[] b;
		Count_Inversion_pair = 0;
	}
	return 0;
}

输出前m大的数

描述
给定一个数组包含n个元素，统计前m大的数并且把这m个数从大到小输出
输入
第一行包含一个整数n，表示数组的大小。n<100000
第二行包含n个整数，表示数组的元素，整数之间以一个空格分开
每个整数的绝对值不超过100000000
第三行包含一个整数m
m<n
输出
从大到小输出前m大的数，每个数一行。
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：输出前m个大的数.cpp

解题思路：
排序后再输出，复杂度O(nlogn)
分治处理：复杂度O(n+mlogm)
注：m<<n 则接近O(n)  否则m→n复杂度O(nlogn)

把前m大的都弄到数组最右边，然后对这最右边m个元素排序，在输出

关键：O(n)时间内实现把前m大的都弄到数组最右边

引入操作 ArrangeRight(k):把数组(或数组的一部分)前k大的都弄到最右边

如何将前k大的都弄到最右边
①设key=a[0]，将key挪到适当位置，使得比key小的元素都在key左边，比key大的元素都在key右边（线性时间完成）
②选择数组的前部或后部再进行ArrangeRight操作

以下步骤递归：
a1,a2,...,am,key,b1,b2,...,bn-1
n=k done
n>k 对右边n-1个元素再进行ArrangeRight(k)
n<k 对左边m个元素再进行ArrangeRight(k-a)，并对右边的元素进行排序

选出k个数后再进行快速排序

时间复杂度：
假设每次都是一半进行排序
T(n) = t(n/2) + a *n
=T(n/4) + a * n/2 + a * n
=T(n/8) + a * n /2 + a * n
=...
=T(1) + ... + a * n/8 + a * n/2 + a *n
<2 * a *n
即O(n)

MOOC的AC了！！！杭电无法AC，超时！
还是超时！无法AC！同学说要用hash，哦呵呵！！！
题目地址：
http://acm.hdu.edu.cn/showproblem.php?pid=1425

当前版本：1.0
作    者：Louris
完成日期：2017.08.10
*/

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
typedef int Status;
#define OK 1
#define ERROR 0

int Partition(vector<int> &a, int low, int high)
{
	//默认参照数为a[low]
	while (low < high)
	{
		while (low < high&&a[low] <= a[high])
		{
			--high;
		}
		swap(a[low], a[high]);
		while (low < high&&a[low] <= a[high])
		{
			++low;
		}
		swap(a[low], a[high]);
	}
	return low;
}


Status QSort(vector<int> &a, int low, int high)
{
	if (low < high)
	{
		int pivotloc = Partition(a, low, high);
		QSort(a, low, pivotloc - 1);
		QSort(a, pivotloc + 1, high);
	}
	return OK;
}

Status ArrangeRight(vector<int> &a, int low, int high, int k)
{
	int pivotloc = Partition(a, low, high);
	if ((high - pivotloc + 1) == k)
	{
		return OK;
	}
	else if (high - pivotloc + 1 > k)
	{
		ArrangeRight(a, pivotloc + 1, high, k);
	}
	else
	{
		ArrangeRight(a, low, pivotloc - 1, k - (high - pivotloc + 1));
	}
	return OK;
}

int main()
{
	vector<int> a;
	int n, m;

	while (cin >> n>>m)
	{
		for (int i = 0; i < n; i++)
		{
			int b;
			cin >> b;
			a.push_back(b);
		}

		ArrangeRight(a, 0, n - 1, m); //选出m个最大数至数组最右边
		QSort(a, n - m, n - 1); //将这m个数进行排序

		for (int i = n - 1; i >= n - m; i--)
		{
			cout << a[i];
			if (i != n - m)
			{
				cout <<" ";
			}
		}
		cout << endl;
		a.clear();
	}
	return 0;
}

第四章动态规划

概述

递归到动规的一般转化方法
　递归函数有n个参数，就定义一个n维的数组，数组的下标是递归函数的参数的取值范围，数组元素的值时递归函数的返回值，这样就可以从边界值开始，逐步填充数组，相当于计算递归函数值的逆过程。

动规解题的一般思路
　①将原问题分解为子问题
　a.把原问题分解为若干个子问题，子问题和原问题形式相同或类似，只不过规模变小了。子问题都解决，原问题即解决。
　b.子问题的解一旦求出就会被保存，所以每个子问题只需求解一次。
　②确定状态
　a.在用动态规划解题时，我们往往将和子问题相关的各个变量的一组取值，称之为一个“状态”。一个“状态”对应于一个或多个子问题，所谓某个“状态”下的“值”，就是这个“状态”所对应的子问题的解。
　b.整个问题的时间复杂度是状态数目乘以计算每个状态所需时间。
　c.在数字三角形里每个“状态”只需要经过一次，且在每个状态上作计算所花的时间都是和N无关的常数。
　d.用动态规划解题，经常碰到的情况是，K个整型变量能构成一个状态（如数字三角形中的行号和列号这两个变量构成“状态”）。如果这K个整型变量的取值范围分别是N1，N2，……，Nk，那么，我们就可以用一个K维数组array[N1][N2]…[Nk]来存储各个状态的“值”。这个“值”未必就是一个整数或浮点数，可能是需要一个结构才能表示的，那么array就可以是一个结构数组。一个“状态”下的“值”通常会是一个或多个子问题的解。
　③确定一些初始状态（边界状态）的值
以“数字三角形”为例，初始状态就是底边数字，值就是底边数字值。
　④确定状态转移方程
即如何从一个或多个“值”已知的”状态“，求出另一个“状态”的值。状态的迁移可以用递推公示表示，此递推公示也可被称作“状态转移方程”。
数字三角形的状态转移方程：
MaxSum[r][j]=
{
D[r][j] r=N
Max{MaxSum[r+1][j],MaxSum[r+1][j+1]+D[r][j]} 其他情况
}

能用动规解决的问题的特点
①问题具有最优子结构性质
如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质。
②无后效性
当前的若干个状态值一旦确定，则此后过程的演变就只和这若干个状态的值有关，和之前是采取哪种手段或经过哪条路径演变到当前的这若干个状态，没有关系。

动规的常用两种形式
1）递归型
优点：直观，容易编写
缺点：可能会因递归层数太深导致爆栈，函数调用带来额外时间开销。无法使用滚动数组节省空间。总体来看，比递推型慢。
2）递推型
效率高，有可能使用滚动数组节省空间

数字三角形

描述
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
在上面的数字三角形中寻找一条从顶部到底边的路径，使得路径上所经过的数字之和最大。路径上的每一步都只能往左下或右下走。只需要求出这个最大和即可，不必给出具体路径。
三角形的行数大于1小于等于100，数字为0-99
输入
5 //三角形行数。
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输出
求出最大和
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：数字三角形.cpp

解题思路：
用二维数组存放数字三角形
D(r,j)：第r行第j个数字(r,j从1开始算)
MaxSum(r,j)：从D(r,j)到底边的各条路径中，最佳路径的数字之和。
问题：求MaxSum(1,1)

典型递归问题。
D(r,j)触发，下一步只能走D(r+1,j)或者D(r+1,j+1)。故对于N行的三角形：
if(r==N)
{
  MaxSum(r,j)=D(r,j);
}
else
{
  MaxSum(r,j)=Max{MaxSum(r+1,j),MaxSum(r+1,j+1)}+D(r,j);
}

注意：超时！重复计算！
如果采用递归的方法，深度遍历每条路径，存在大量重复计算，则时间复杂度为2^n，对于n=100肯定超时。

改进：
如果每算出一个MaxSum(r,j)就保存起来，下次用到其值的时候直接取用，则可免去重复计算。
那么可用O(n^2)时间完成计算。因为三角形的数字总数是n(n+1)/2。

参见下个版本程序

当前版本：1.0
作    者：Louris
完成日期：2017.08.13
*/
#include<iostream>
#include<algorithm>
using namespace std;
const int MAX = 100;
typedef int Status;
#define OK 1
#define ERROR 0
int D[MAX][MAX];
int n;
int MaxSum(int i, int j)
{
	if (i == n-1)
	{
		return D[i][j];
	}
	return max(MaxSum(i + 1, j), MaxSum(i + 1, j + 1)) + D[i][j];
}
int main()
{
	int i, j;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j <= i; j++)
		{
			cin >> D[i][j];
		}
	}
	cout << MaxSum(0, 0) << endl;
	return 0;
}

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：数字三角形_动态规划版.cpp

解题思路：
用二维数组存放数字三角形
D(r,j)：第r行第j个数字(r,j从1开始算)
MaxSum(r,j)：从D(r,j)到底边的各条路径中，最佳路径的数字之和。
问题：求MaxSum(1,1)

典型递归问题。
D(r,j)触发，下一步只能走D(r+1,j)或者D(r+1,j+1)。故对于N行的三角形：
if(r==N)
{
MaxSum(r,j)=D(r,j);
}
else
{
MaxSum(r,j)=Max{MaxSum(r+1,j),MaxSum(r+1,j+1)}+D(r,j);
}

注意：超时！重复计算！
如果采用递归的方法，深度遍历每条路径，存在大量重复计算，则时间复杂度为2^n，对于n=100肯定超时。

改进：
如果每算出一个MaxSum(r,j)就保存起来，下次用到其值的时候直接取用，则可免去重复计算。
那么可用O(n^2)时间完成计算。因为三角形的数字总数是n(n+1)/2。

当前版本：1.0
作    者：Louris
完成日期：2017.08.13
*/

#include<iostream>
#include<algorithm>
using namespace std;
const int MAX = 100;
typedef int Status;
#define OK 1
#define ERROR 0
int D[MAX][MAX];
int n;
int maxSum[MAX][MAX];

int MaxSum(int i, int j)
{
	if (maxSum[i][j] != -1)
	{
		return maxSum[i][j];
	}

	if (i == n - 1)
	{
		return D[i][j];
	}
	else
	{
		maxSum[i][j] = max(MaxSum(i + 1, j), MaxSum(i + 1, j + 1)) + D[i][j];
	}

	return maxSum[i][j];
}

int main()
{
	int i, j;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j <= i; j++)
		{
			cin >> D[i][j];
			maxSum[i][j] = -1;
		}
	}
	cout << MaxSum(0, 0) << endl;
	return 0;
}

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：数字三角形_递推版.cpp

解题思路：
用二维数组存放数字三角形
D(r,j)：第r行第j个数字(r,j从1开始算)
MaxSum(r,j)：从D(r,j)到底边的各条路径中，最佳路径的数字之和。
问题：求MaxSum(1,1)

典型递归问题。
D(r,j)触发，下一步只能走D(r+1,j)或者D(r+1,j+1)。故对于N行的三角形：
if(r==N)
{
MaxSum(r,j)=D(r,j);
}
else
{
MaxSum(r,j)=Max{MaxSum(r+1,j),MaxSum(r+1,j+1)}+D(r,j);
}

注意：超时！重复计算！
如果采用递归的方法，深度遍历每条路径，存在大量重复计算，则时间复杂度为2^n，对于n=100肯定超时。

改进：
如果每算出一个MaxSum(r,j)就保存起来，下次用到其值的时候直接取用，则可免去重复计算。
那么可用O(n^2)时间完成计算。因为三角形的数字总数是n(n+1)/2。

递归转成递推：
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

30
23 21
20 13 10
 7 12 10 10
 4  5  2  6  5

由递归思路从上往下，
而实质则是递推的思路从下往上
即先进行下层的各元素的最大和，逐级向上计算

当前版本：1.0
作    者：Louris
完成日期：2017.08.18
*/
#include<iostream>
#include<algorithm>
using namespace std;
#define MAX 101
int D[MAX][MAX];
int n;
int maxSum[MAX][MAX];
int main()
{
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j <= i; j++)
		{
			cin >> D[i][j];
		}
	}
	for (int i = 0; i < n; i++)
	{
		maxSum[n - 1][i] = D[n - 1][i];
	}
	for (int i = n - 2; i >= 0; i--)
	{
		for (int j = 0; j <= i; j++)
		{
			maxSum[i][j] = max(maxSum[i + 1][j],maxSum[i + 1][j + 1]) + D[i][j];
		}
	}
	cout << maxSum[0][0] << endl;
	return 0;
}

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：数字三角形_空间优化版.cpp

解题思路：
用二维数组存放数字三角形
D(r,j)：第r行第j个数字(r,j从1开始算)
MaxSum(r,j)：从D(r,j)到底边的各条路径中，最佳路径的数字之和。
问题：求MaxSum(1,1)

典型递归问题。
D(r,j)触发，下一步只能走D(r+1,j)或者D(r+1,j+1)。故对于N行的三角形：
if(r==N)
{
MaxSum(r,j)=D(r,j);
}
else
{
MaxSum(r,j)=Max{MaxSum(r+1,j),MaxSum(r+1,j+1)}+D(r,j);
}

注意：超时！重复计算！
如果采用递归的方法，深度遍历每条路径，存在大量重复计算，则时间复杂度为2^n，对于n=100肯定超时。

改进：
如果每算出一个MaxSum(r,j)就保存起来，下次用到其值的时候直接取用，则可免去重复计算。
那么可用O(n^2)时间完成计算。因为三角形的数字总数是n(n+1)/2。

递归转成递推：
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

30
23 21
20 13 10
7 12 10 10
4  5  2  6  5

由递归思路从上往下，
而实质则是递推的思路从下往上
即先进行下层的各元素的最大和，逐级向上计算

空间优化：
没必要用二维maxSum数组存储每一个MaxSum(r,j)，只要从底层一行行向上递推，那么
只要一维数组maxSum[100]即可，即只要存储一行的MaxSum值就行。

7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

7
30  8
23 21  0
20 13 10  4
 7 12 10 10 5

进一步考虑，连maxSum数组都可以不要，直接用D的第n行替代maxSum即可。
节省空间，时间复杂度不变。

当前版本：1.0
作    者：Louris
完成日期：2017.08.19
*/

#include<iostream>
#include<algorithm>
using namespace std;
#define MAX 101
int D[MAX][MAX];
int n;
int *maxSum;
int main()
{
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j <= i; j++)
		{
			cin >> D[i][j];
		}
	}
	maxSum = D[n-1]; //maxSum指向第n行
	for (int i = n - 2; i >= 0; i--)
	{
		for (int j = 0; j <= i; j++)
		{
			maxSum[j] = max(maxSum[j], maxSum[j + 1]) + D[i][j];
		}
	}
	cout << maxSum[0] << endl;
	return 0;
}

最长上升子序列

描述
一个数的序列ai，当a1<a2<…<as的时候，我们称这个序列是上升的。对于给定的一个序列（a1,a2,…,aN），我们可以得到一些上升的子序列（ai1,ai2,…,aiK），这里1<=i1<i2<…<iK<=N。比如，对于序列（1,7,3,5,9,4,8），有它的一些上升子序列，如（1,7），（3,4,8）等等。这些子序列中最长的长度是4，比如子序列（1,3,5,8）。
你的任务，就是对于给定的序列，求出最长上升子序列的长度。
输入数据
输入的第一行是序列的长度N（1<=N<=1000）。第二行给出序列中的N个整数，这些整数的取值范围都在0到10000.
输出要求
最长上升子序列的长度。
输入样例
7
1 7 3 5 9 4 8
输出样例
4
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：最长上升子序列.cpp

解题思路：
1.找子问题
①“求序列的前n个元素的最长上升子序列的长度”是个子问题，但这样分解子问题，不具有“无后效性”
假设F(n)=x，但可能有多个序列满足F(n)=x。有的序列最后一个元素比an+1小，则加上an+1就能形成更长上升
子序列；有的序列最后一个元素不比an+1小……以后的事情受如何达到状态n的影响，不符合“无后效性”。

②“求以ak(k=1,2,3,...,N)为终点的最长上升子序列的长度”。
一个上升子序列中最右边的那个数，称为该子序列的“终点”。
虽然这个子问题和原问题形式上并不完全一样，但是只要这N个子问题都解决了，
那么这N个子问题的解中，最大的那个就是整个问题的解。

2.确定状态
子问题只和一个变量——数字的位置相关。因此序列中数的位置k就是“状态”，
而状态k对应的“值”，就是以ak作为“终点”的最长上升子序列的长度。
状态一共有N个。

3.找出状态转移方程
maxLen(k)表示以ak为“终点”的最长上升子序列的长度：
初始状态：maxLen(i)=1
maxLen(k)=max{maxLen(i):1<=i<k且ai<ak且k≠1}+1
若找不到这样的i，则maxLen(k)=1

maxLen(k)的值，就是在ak左边，“终点”数值小于ak，且长度最大的那个上升子序列的长度再加1。
因为ak左边任何“终点”小于ak的子序列，加上ak后就能形成一个更长的上升子序列。

当前版本：1.0
作    者：Louris
完成日期：2017.08.20
*/

#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN = 1010;
int a[MAXN];
int maxLen[MAXN];
int main()
{
	int N;
	cin >> N;
	for (int i = 1; i <= N; ++i)
	{
		cin >> a[i];
		maxLen[i] = 1;
	}

  //枚举所有状态
	for (int i = 2; i <= N; ++i)
	{
		//每次求以第i个数为终点的最长上升子序列的长度
		for (int j = 1; j < i; ++j)
		{
			//查看以第j个数为终点的最长上升子序列
			if (a[i] > a[j])
			{
				maxLen[i] = max(maxLen[i], maxLen[j] + 1);
			}
		}
	}

	cout << *max_element(maxLen + 1, maxLen + N + 1);
	return 0;
}//时间复杂度O(N^2)

最长公共子序列

描述
给出两个字符串，求出这样的一个最长的公共子序列的长度：子序列中的每个字符都能在两个原串中找到，而且每个字符的先后顺序和原串中的先后顺序一致。
Sample Input
abcfbc abfcab
programming contest
abcd mnp
Sample Output
4
2
0
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：最长公共子序列.cpp

解题思路：
输入两个字符串s1,s2
设MaxLen(i,j)表示：
s1的左边i个字符形成的子串，与s2左边的j个字符形成的子串的最长公共子序列的长度
(i,j从0开始算)
MaxLen(i,j)就是本题的“状态”

假定len1=strlen(s1),len2=strlen(s2)
那么题目就是要求MaxLen(len1,len2)
显然：
MaxLen(n,0) = 0 (n=0...len1)
MaxLen(0,n) = 0 (n=0...len2)
递推公式：
if(s1[i-1]==s2[j-1])
  MaxLen(i,j) = MaxLen(i-1,j-1) + 1
else
  MaxLen(i,j) = Max(MaxLen(i,j-1),MaxLen(i-1,j))
时间复杂度：O(mn) m,n是两个字串长度

s1[i-1] != s2[j-1]时，MaxLen(s1,s2)不会比MaxLen(s1,s2j-1)
和MaxLen(s1i-1,s2)两者之中任何一个小，也不会比两者都大。

当前版本：1.0
作    者：Louris
完成日期：2017.08.21
*/
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
string s1;
string s2;
int maxLen[1000][1000];
int main()
{
	while (cin >> s1 >> s2)
	{
		//边界条件
		for (unsigned int i = 0; i <= s1.length(); i++)
		{
			maxLen[i][0] = 0;
		}
		for (unsigned int j = 0; j <= s2.length(); j++)
		{
			maxLen[0][j] = 0;
		}

		//枚举所有状态
		for (unsigned int i = 1; i <= s1.length(); i++)
		{
			for (unsigned int j = 1; j <= s2.length(); j++)
			{
				if (s1[i-1] == s2[j-1])
				{
					maxLen[i][j] = maxLen[i - 1][j - 1] + 1;
				}
				else
				{
					maxLen[i][j] = max(maxLen[i][j - 1], maxLen[i - 1][j]);
				}
			}
		}
		//输出
		cout << maxLen[s1.length()][s2.length()] << endl;
	}
	return 0;
}

最佳加法表达式

描述
　　给定n个1到9的数字，要求在数字之间摆放m个加号(加号两边必须有数字），使得所得到的加法表达式的值最小，并输出该值。例如，在1234中摆放1个加号，最好的摆法就是12+34,和为36
输入
　　有不超过15组数据
　　每组数据两行。第一行是整数m，表示有m个加号要放( 0<=m<=50)
　　第二行是若干个数字。数字总数n不超过50,且 m <= n-1
输出
对每组数据，输出最小加法表达式的值
样例输入
2
123456
1
123456
4
12345
样例输出
102
579
15
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：最佳加法表达式.cpp

解题思路：
假定数字串的长度是n，添完加号后，表达式的最后一个加号添加在第i个数字后面，
那么整个表达式的最小值，就等于在前i个数字中插入m-1个加号所能形成的最小值，
加上第i+1到第n个数字所组成的数的值（i从1开始算）。

设V(m,n)表示在n个数字中插入m个加号所能形成的表达式最小值，那么：
if(m=0)
V(m,n)=n个数字构成的整数
else if(n < m + 1)
V(m,n))=∞
else
V(m,n)=Min{V(m-1,i)+Num(i+1,n)}(i=m...n-1)
（因为满足能插入m个加号，那么先进行最后一个加号后再进行m-1个加号的分配中，
必须要满足剩余数字个数必须能插入m-1个加号，所以i最少m，最大n-1不难理解）

Num(i,j)表示从第i个数字到第j个数字所组成的数。
数字编号从1开始算。
此操作复杂度是O(j-i+1)，可以预处理后存起来。
总时间复杂度：O(mn^2)。

若n比较大，longlong不够存放运算过程中的整数，则需要使用高精度计算
（用数组存放打证书，模拟列竖式做加法），复杂度为O(mn^3)

当前版本：1.0
作    者：Louris
完成日期：2017.08.27
*/

#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
#include<vector>
#include<limits.h>
using namespace std;
#include"BigInteger.h" //参见算法导论/常用函数库/BigInteger.h
#define OK 1
#define ERROR 0
typedef int Status;
using namespace std;
string str;
unsigned int m;
BigInteger Num[51][51];
BigInteger V[51][51];
string MAX = "999999999999999999999999999999999999999999999999999";

int main()
{
	while (cin >> m >> str)
	{
		//初始化Num
		for (unsigned int i = 1; i <= str.length(); i++)
		{
			for (unsigned int j = i; j <= str.length(); j++)
			{
				Num[i][j] = BigInteger(str.substr(i - 1, j - i + 1));
			}
		}

		//m=0,边界条件
		for (unsigned int i = 1; i <= str.length(); i++)
		{
			V[0][i] = BigInteger(str.substr(0, i));
		}

		//最外层两层循环枚举所有V(m,n)，即Min{}所有状态枚举
		for (unsigned int i = 1; i <= m; i++)
		{
			for (unsigned int j = 1; j <= str.length(); j++)
			{
				if (j < i + 1)
				{
					V[i][j] = BigInteger(MAX);
				}
				else
				{
					//找出当前最小值
					BigInteger tempMin = MAX;
					//(i=m...n-1)
					for (unsigned int k = i; k<str.length(); k++)
					{
						BigInteger temp = V[i - 1][k] + Num[k + 1][j];
						if (temp < tempMin)
						{
							tempMin = temp;
						}
					}
					V[i][j] = tempMin;
				}
			}
		}
		cout << V[m][str.length()] << endl;
	}
	return 0;
}

最大序列和

线性复杂度

int max_Sub(int a[],int size)
{
  int max=0,temp_sum=0;
  for(int i=0;i<size;i++)
  {
    temp_sum+=a[i];
    if(temp_sum>max)//记录最大和，保证了序列和连续
    {
      max=temp_sum;
    }
    else if(temp_sum<0)//负数则重新计算
    {
      temp_sum=0;
    }
  }
  return temp_sum;
}

int max_Sub(int a[],int size){
  int dp[size];
  dp[0]=a[0];
  for(int i=1;i<size;i++){
    dp[i]=max(a[i],dp[i-1]+a[i]);
  }
  int k=0;
  for(int i=0;i<size;i++){
    if(dp[i]>dp[k]){
      k=i;
    }
  }
  return dp[k];
}

Max Sum

Problem Description
Given a sequence a[1],a[2],a[3]……a[n], your job is to calculate the max sum of a sub-sequence. For example, given (6,-1,5,4,-7), the max sum in this sequence is 6 + (-1) + 5 + 4 = 14.
Input
The first line of the input contains an integer T(1<=T<=20) which means the number of test cases. Then T lines follow, each line starts with a number N(1<=N<=100000), then N integers followed(all the integers are between -1000 and 1000).
OutPut
For each test case, you should output two lines. The first line is “Case #:”, # means the number of the test case. The second line contains three integers, the Max Sum in the sequence, the start position of the sub-sequence, the end position of the sub-sequence. If there are more than one result, output the first one. Output a blank line between two cases.
Sample Input
2
5 6 -1 5 4 -7
7 0 6 -1 1 -6 7 -5
Sample Output
Case 1:
14 1 4

Case 2:
7 1 6
Procedure

/*
	Copyright(c)2017, Louris
	All rights reserved.
	文件名称：1003.cpp
	摘    要：
		杭电OJ 1003题
	解题思路：
		题目求给定序列的子序列的最大和，故必须是连续序列。
		输出要求输出最大和及其始终位置。
		模拟如下：
		1.输入第一个数，始终位置初始化，最大和初始化；
		2.输入第二个数，求得当前值与之前暂存和的当前和，比较之：
			①若当前数值大于当前和，则更新之前暂存和的开始位置，因为此时说明之前暂存最大和小于0，应当舍弃，以当前数的值为暂存最大和，当前位置为暂存最大和的起始位置，更新暂存最大和的最终位置
			②否则，之前暂存和加上当前数值，暂存最大和起始位置不变，更新暂存最大和的最终位置。
			③暂存最大和与最大和比较，若大于，则更新最大和。
		3.重复步骤2，直至当前序列输出结束，输出结果。
	当前版本：1.0
	作    者：Louris
	完成日期：2017.07.15
*/
#include<iostream>
using namespace std;
int main()
{
	int T;
	cin >> T;
	int flag = 1;
	while (T--)
	{
		int N;
		int max, pre_max;//记录当前最大值，先前最大值
		int start, pre_start, end;//记录当前最大值起始位置，之前最大值起始位置，最大值结束位置
		int sum = 0;
		cin >> N;
		for (int i = 1; i <= N; i++)
		{
			int now;
			cin >> now;
			if (i == 1)
			{
				max = pre_max = now;
				start = pre_start = end = i;
			}
			else
			{
				if (/*now > now + pre_max*/pre_max < 0)
				{
					pre_max = now;
					pre_start = i;
				}
				else
				{
					pre_max += now;
				}
			}
			if (pre_max > max)
			{
				max = pre_max;
				start = pre_start;
				end = i;
			}
		}
		cout << "Case " << flag++ << ":" << endl
			<< max << " " << start << " " << end << endl;
		if (T != 0)
		{
			cout << endl;
		}
	}
	return 0;
}

最大子矩阵

描述
已知矩阵的大小定义为矩阵中所有元素的和。给定一个矩阵，你的任务是找到最大的非空(大小至少是1 × 1)子矩阵。
比如，如下4 × 4的矩阵
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
的最大子矩阵是
9 2
-4 1
-1 8
这个子矩阵的大小是15。
输入
输入是一个N × N的矩阵。输入的第一行给出N (0 < N <= 100)。再后面的若干行中，依次（首先从左到右给出第一行的N个整数，再从左到右给出第二行的N个整数……）给出矩阵中的N2个整数，整数之间由空白字符分隔（空格或者空行）。已知矩阵中整数的范围都在[-127, 127]。
输出
输出最大子矩阵的大小。
样例输入
4
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
样例输出
15
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：最大子矩阵.cpp

解题思路：
第一反应就是一维的最大序列和问题
那么这里推广到二维如何进行？
降维：
假设最优解在第i行和第j行之间，那么只需对这些行对应列求和，然后转换成一维最大序列和！

当前版本：1.0
作    者：Louris
完成日期：2017.09.24
*/
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int MAXN = 101;
int Matrix[MAXN][MAXN];
int dp[MAXN];
int n;
int max_Sub(int d[], int size)
{
	int max = 0, temp_sum = 0;
	for (int i = 0; i < size; i++)
	{
		temp_sum += d[i];
		if (temp_sum > max)
		{
			max = temp_sum;
		}
		else if (temp_sum < 0)
		{
			temp_sum = 0;
		}
	}
	return max;
}
int main()
{
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			cin >> Matrix[i][j];
		}
	}
	int maxSum = 0;
	for (int i = 0; i < n; i++)//开始行
	{
		memset(dp, 0, sizeof(dp));
		for (int j = i; j < n; j++)//结束行
		{
			for (int k = 0; k < n; k++)//列循环
			{
				dp[k] += Matrix[j][k];
			}
			maxSum = max(maxSum, max_Sub(dp, n));
		}
	}
	cout << maxSum << endl;
	return 0;
}

拦截导弹

描述
某国为了防御敌国的导弹袭击，开发出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭，并观测到导弹依次飞来的高度，请计算这套系统最多能拦截多少导弹。拦截来袭导弹时，必须按来袭导弹袭击的时间顺序，不允许先拦截后面的导弹，再拦截前面的导弹。
输入
输入有两行，
第一行，输入雷达捕捉到的敌国导弹的数量k（k<=25），
第二行，输入k个正整数，表示k枚导弹的高度，按来袭导弹的袭击时间顺序给出，以空格分隔。
输出
输出只有一行，包含一个整数，表示最多能拦截多少枚导弹。
样例输入
8
300 207 155 300 299 170 158 65
样例输出
6
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：拦截导弹.cpp

解题思路：
即找最长下降子序列
1.找子问题
“求以ak(k=1,2,3,...,N)为终点的最长下降子序列的长度”
一个下降子序列中最右边的那个数，称为该子序列的“终点”
那么这个N个子问题的解中，最大的那个就是整个问题的解。

2.确定状态
子问题只和一个变量——数字的位置相关。
因此序列中数的位置k就是“状态”，而状态k对应的“值”，就是以ak为“终点”的最长下降子序列的长度。
状态一共有N个。

3.找出状态转移方程
maxLen(k)表示以ak为“终点”的最长上升子序列的长度：
初始状态：maxlen(i)=1
maxLen(k)=max{maxLen(i):1<=i<k且ai>ak且k≠1}+1
若找不到这样的i，则maxLen(k)=1


当前版本：1.0
作    者：Louris
完成日期：2017.08.29
*/

#include<iostream>
#include<algorithm>
#define OK 1
#define ERROR 0
typedef int Status;
using namespace std;
const int MAXN = 26;
int a[MAXN];
int maxLen[MAXN];
int N;
int main()
{
	while (cin >> N)
	{
		for (int i = 1; i <= N; i++)
		{
			cin >> a[i];
			maxLen[i] = 1;
		}
		for (int i = 2; i <= N; i++)
		{
			for (int j = 1; j < i; j++)
			{
				if (a[i] <= a[j])
				{
					maxLen[i] = max(maxLen[i], maxLen[j] + 1);
				}
			}
		}
		cout << *max_element(maxLen + 1, maxLen + N + 1);
	}
	return 0;
}

大盗阿福

描述
阿福是一名经验丰富的大盗。趁着月黑风高，阿福打算今晚洗劫一条街上的店铺。
这条街上一共有 N 家店铺，每家店中都有一些现金。阿福事先调查得知，只有当他同时洗劫了两家相邻的店铺时，街上的报警系统才会启动，然后警察就会蜂拥而至。
作为一向谨慎作案的大盗，阿福不愿意冒着被警察追捕的风险行窃。他想知道，在不惊动警察的情况下，他今晚最多可以得到多少现金？
输入
输入的第一行是一个整数 T (T <= 50) ，表示一共有 T 组数据。
接下来的每组数据，第一行是一个整数 N (1 <= N <= 100, 000) ，表示一共有 N 家店铺。第二行是 N 个被空格分开的正整数，表示每一家店铺中的现金数量。每家店铺中的现金数量均不超过 1000 。
输出
对于每组数据，输出一行。该行包含一个整数，表示阿福在不惊动警察的情况下可以得到的现金数量。
样例输入
2
3
1 8 2
4
10 7 6 14
样例输出
8
24
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：大盗阿福.cpp

解题思路：
动态规划
第i家店盗窃金额=第i-2家店盗窃金额+第i-3家店盗窃金额
d(i)=max{d(i-2)+money(i),d(i-3)+moeny(i)}
因为i->i-2->i-4/i-5
i->i-3->i-5/i-6


当前版本：1.0
作    者：Louris
完成日期：2017.09.23
*/
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int T;
int N;
int money[100001];
int d[100001];
int result;
int main()
{
	cin >> T;
	while (T--)
	{
		cin >> N;
		memset(d, 0, sizeof(d));
		result = 0;
		for (int i = 0; i < N; i++)
		{
			cin >> money[i];
			d[i] = money[i];
		}
		d[2] += d[0];
		result = max(d[0], d[1]);
		result = max(result, d[2]);
		for (int i = 3; i < N; i++)
		{
			d[i] += max(d[i - 2], d[i - 3]);
			result = max(result, d[i]);
		}
		cout << result << endl;
	}
	return 0;
}

鸣人的影分身

描述
在火影忍者的世界里，令敌人捉摸不透是非常关键的。我们的主角漩涡鸣人所拥有的一个招数——多重影分身之术——就是一个很好的例子。
影分身是由鸣人身体的查克拉能量制造的，使用的查克拉越多，制造出的影分身越强。
针对不同的作战情况，鸣人可以选择制造出各种强度的影分身，有的用来佯攻，有的用来发起致命一击。
那么问题来了，假设鸣人的查克拉能量为M，他影分身的个数为N，那么制造影分身时有多少种（用K表示）不同的分配方法？（影分身可以被分配到0点查克拉能量）
输入
第一行是测试数据的数目t（0 <= t <= 20）。以下每行均包含二个整数M和N，以空格分开。1<=M，N<=10。
输出
对输入的每组数据M和N，用一行输出相应的K。
样例输入
1
7 3
样例输出
8
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：鸣人的影分身.cpp

解题思路：
动规：
设i个查克拉分给j个分身为f[i][j]
则
总数=每个分身非空+至少一个分身为空
f[i][j]=f[i-j][j]+f[i][j-1]

边界：
f[0][j]=1
f[i][0]=0(i≠0)
i<j f[i][j]=f[i][i]

当前版本：1.0
作    者：Louris
完成日期：2017.09.23
*/
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int t, m, n;
int d[11][11];
int main()
{
	cin >> t;
	while (t--)
	{
		cin >> m >> n;
		memset(d, 0, sizeof(d));
		for (int i = 0; i <= n; i++)
		{
			d[0][i] = 1;
		}
		for (int i = 1; i <= m; i++)
		{
			for (int j = 1; j <= n; j++)
			{
				if (i < j)
				{
					d[i][j] = d[i][i];
				}
				else
				{
					d[i][j] = d[i - j][j] + d[i][j - 1];

				}
			}
		}
		cout << d[m][n] << endl;
	}
	return 0;
}

开餐馆

描述
北大信息学院的同学小明毕业之后打算创业开餐馆.现在共有n 个地点可供选择。小明打算从中选择合适的位置开设一些餐馆。这 n 个地点排列在同一条直线上。我们用一个整数序列m1, m2, … mn 来表示他们的相对位置。由于地段关系,开餐馆的利润会有所不同。我们用pi 表示在mi 处开餐馆的利润。为了避免自己的餐馆的内部竞争,餐馆之间的距离必须大于k。请你帮助小明选择一个总利润最大的方案。
输入
标准的输入包含若干组测试数据。输入第一行是整数T (1 <= T <= 1000) ，表明有T组测试数据。紧接着有T组连续的测试。每组测试数据有3行,
第1行:地点总数 n (n < 100), 距离限制 k (k > 0 && k < 1000).
第2行:n 个地点的位置m1 , m2, … mn ( 1000000 > mi > 0 且为整数,升序排列)
第3行:n 个地点的餐馆利润p1 , p2, … pn ( 1000 > pi > 0 且为整数)
输出
对于每组测试数据可能的最大利润
样例输入
2
3 11
1 2 15
10 2 30
3 16
1 2 15
10 2 30
样例输出
40
30
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：开餐馆.cpp

解题思路：
动规：
设位置i的利润d[i]：
d[i]=max(d[i],d[j]+v[i])

与最长上升子序列相似

当前版本：1.0
作    者：Louris
完成日期：2017.09.23
*/
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int T;
int n;
int k;
int d[101];
int pro[101];
int dis[101];
int main()
{
	cin >> T;
	while (T--)
	{
		cin >> n >> k;
		for (int i = 1; i <= n; i++)
		{
			cin >> dis[i];
		}
		for (int i = 1; i <= n; i++)
		{
			cin >> pro[i];
			d[i] = pro[i];
		}
		for (int i = 1; i <= n; i++)
		{
			for (int j = 1; j <= n; j++)
			{
				if (dis[i] - dis[j] > k)
				{
					d[i] = max(d[i], d[j] + pro[i]);
				}
			}
		}
		int max = *max_element(d + 1, d + 1 + 100);
		cout << max << endl;
	}
	return 0;
}

宠物精灵之收服

描述
宠物小精灵是一部讲述小智和他的搭档皮卡丘一起冒险的故事。
一天，小智和皮卡丘来到了小精灵狩猎场，里面有很多珍贵的野生宠物小精灵。小智也想收服其中的一些小精灵。然而，野生的小精灵并不那么容易被收服。对于每一个野生小精灵而言，小智可能需要使用很多个精灵球才能收服它，而在收服过程中，野生小精灵也会对皮卡丘造成一定的伤害（从而减少皮卡丘的体力）。当皮卡丘的体力小于等于0时，小智就必须结束狩猎（因为他需要给皮卡丘疗伤），而使得皮卡丘体力小于等于0的野生小精灵也不会被小智收服。当小智的精灵球用完时，狩猎也宣告结束。
我们假设小智遇到野生小精灵时有两个选择：收服它，或者离开它。如果小智选择了收服，那么一定会扔出能够收服该小精灵的精灵球，而皮卡丘也一定会受到相应的伤害；如果选择离开它，那么小智不会损失精灵球，皮卡丘也不会损失体力。
小智的目标有两个：主要目标是收服尽可能多的野生小精灵；如果可以收服的小精灵数量一样，小智希望皮卡丘受到的伤害越小（剩余体力越大），因为他们还要继续冒险。
现在已知小智的精灵球数量和皮卡丘的初始体力，已知每一个小精灵需要的用于收服的精灵球数目和它在被收服过程中会对皮卡丘造成的伤害数目。请问，小智该如何选择收服哪些小精灵以达到他的目标呢？
输入
输入数据的第一行包含三个整数：N(0 < N < 1000)，M(0 < M < 500)，K(0 < K < 100)，分别代表小智的精灵球数量、皮卡丘初始的体力值、野生小精灵的数量。
之后的K行，每一行代表一个野生小精灵，包括两个整数：收服该小精灵需要的精灵球的数量，以及收服过程中对皮卡丘造成的伤害。
输出
输出为一行，包含两个整数：C，R，分别表示最多收服C个小精灵，以及收服C个小精灵时皮卡丘的剩余体力值最多为R。
样例输入
10 100 5
7 10
2 40
2 50
1 20
4 20
10 100 5
8 110
12 10
20 10
5 200
1 110
样例输出
3 30
0 100
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：宠物小精灵之收服.cpp

解题思路：
0-1背包
设每个小精灵收服所用精灵球为s[i],消耗皮卡丘体力为e[i]
d[i][j][k]表示在这i个小精灵中用皮卡丘体力值j和k精灵球进行收服所获的的最大精灵数
d[i][j][k]=max(d[i-1][j-e[i]][k-s[i]]+1,d[i-1][j][k])
同样采取状态压缩,只需二维就可以了，这里不再过多叙述。

我可能真的是头猪，d[501][1001]写反了，真他妈服！

当前版本：1.0
作    者：Louris
完成日期：2017.09.23
*/
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int N, M, K;
struct Node
{
	int e; //体力
	int s; //精灵球
}node[101];
int d[501][1001];
int main()
{
	while (cin >> N >> M >> K)
	{
		for (int i = 1; i <= K; i++)
		{
			cin >> node[i].s >> node[i].e;
		}
		memset(d, 0, sizeof(d));
		for (int i = 1; i <= K; i++)
		{
			for (int j = M; j >= node[i].e; j--)
			{
				for (int k = N; k >= node[i].s; k--)
				{
					d[j][k] = max(d[j - node[i].e][k - node[i].s] + 1, d[j][k]);
				}
			}
		}
		cout << d[M][N] << " ";

		for (int i = 0; i <= M; i++)
		{
			if (d[i][N] == d[M][N])
			{
				cout << M - i << endl;
				break;
			}

		}
	}
	return 0;
}

Zipper

描述
Given three strings, you are to determine whether the third string can be formed by combining the characters in the first two strings. The first two strings can be mixed arbitrarily, but each must stay in its original order.

For example, consider forming “tcraete” from “cat” and “tree”:
String A: cat
String B: tree
String C: tcraete
As you can see, we can form the third string by alternating characters from the two strings.

As a second example, consider forming “catrtee” from “cat” and “tree”:
String A: cat
String B: tree
String C: catrtee
Finally, notice that it is impossible to form “cttaree” from “cat” and “tree”.
输入
The first line of input contains a single positive integer from 1 through 1000. It represents the number of data sets to follow. The processing for each data set is identical. The data sets appear on the following lines, one data set per line.

For each data set, the line of input consists of three strings, separated by a single space. All strings are composed of upper and lower case letters only. The length of the third string is always the sum of the lengths of the first two strings. The first two strings will have lengths between 1 and 200 characters, inclusive.
输出
For each data set, print:
Data set n: yes
if the third string can be formed from the first two, or
Data set n: no
if it cannot. Of course n should be replaced by the data set number. See the sample output below for an example.
样例输入
3
cat tree tcraete
cat tree catrtee
cat tree cttaree
样例输出
Data set 1: yes
Data set 2: yes
Data set 3: no
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：Zipper.cpp

解题思路：
1.最优子结构分析：
①如果A、B能组成C，那么C的最后一个字母必定是A或B的最后一个字母组成
②C去除最后一位，就变成了A-1和B或者A和B-1是否可以构成C-1
2.状态转移方程：
用Valid[i][j]表示A前i位和B前j为是否可以组成C的前i+j位：
Valid[i][j]=（a[i-1]==c[i+j-1]&&Valid[i-1][j])||(b[j-1]==c[i+j-1]&&Valid[i][j-1]);

边界条件：
if(a[i-1]==c[i-1]) Valid[i][0]=true;
if(b[j-1[==c[j-1]) Valid[0][j]=true;

当前版本：1.0
作    者：Louris
完成日期：2017.08.29
*/
#include<iostream>
#include<string>
using namespace std;
string a, b, c;
bool Valid[201][201];
int n;
int main()
{
	while (cin >> n)
	{
		for (int x = 1; x <= n; x++)
		{
			cin >> a >> b >> c;
			//边界
			for (unsigned int i = 1; i <= a.length(); i++)
			{
				if (a[i - 1] == c[i - 1])
				{
					Valid[i][0] = true;
				}
			}
			for (unsigned int j = 1; j <= b.length(); j++)
			{
				if (b[j - 1] == c[j - 1])
				{
					Valid[0][j] = true;
				}
			}

			//动规
			for (unsigned int i = 1; i <= a.length(); i++)
			{
				for (unsigned int j = 1; j <= b.length(); j++)
				{
					Valid[i][j] = (a[i - 1] == c[i + j - 1] && Valid[i - 1][j]) || (b[j - 1] == c[i + j - 1] && Valid[i][j - 1]);
				}
			}
			cout << "Data set " << x << ": ";
			if (Valid[a.length()][b.length()])
				cout << "yes" << endl;
			else
				cout << "no" << endl;
		}
	}
	return 0;
}

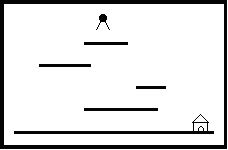
Help Jimmy

描述
“Help Jimmy”是在下图所示的场景上完成的游戏：
　　　　　　　　　　　　　　　　　　　　　　 Help_Jimmy图示
场景中包括多个长度和高度各不相同的平台。地面是最低的平台，高度为零，长度无限。
Jimmy老鼠在时刻0从高于所有平台的某处开始下落，它的下落速度始终为1米/秒。当Jimmy落到某个平台上时，游戏者选择让它向左还是向右跑，它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时，开始继续下落。Jimmy每次下落的高度不能超过MAX米，不然就会摔死，游戏也会结束。
设计一个程序，计算Jimmy到地面时可能的最早时间。
输入
第一行是测试数据的组数t（0 <= t <= 20）。每组测试数据的第一行是四个整数N，X，Y，MAX，用空格分隔。N是平台的数目（不包括地面），X和Y是Jimmy开始下落的位置的横竖坐标，MAX是一次下落的最大高度。接下来的N行每行描述一个平台，包括三个整数，X1[i]，X2[i]和H[i]。H[i]表示平台的高度，X1[i]和X2[i]表示平台左右端点的横坐标。1 <= N <= 1000，-20000 <= X, X1[i], X2[i] <= 20000，0 < H[i] < Y <= 20000（i = 1..N）。所有坐标的单位都是米。

Jimmy的大小和平台的厚度均忽略不计。如果Jimmy恰好落在某个平台的边缘，被视为落在平台上。所有的平台均不重叠或相连。测试数据保证问题一定有解。
输出
对输入的每组测试数据，输出一个整数，Jimmy到底地面时可能的最早时间。
样例输入
1
3 8 17 20
0 10 8
0 10 13
4 14 3
样例输出
23
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：Help_Jimmy.cpp

解题思路：
1.最优子结构：
Jimmy跳到一块板上后，可以有两种选择，向左走，或向右走。
走到左端和走到右端所需的时间，是很容易算得。
如果我们能知道，以左端为起点到达地面的最短时间，和以右端为起点到达地面的最短时间，
那么向左走还是向右走，就很容易选择了。
因此，整个问题就被分解成子问题，即Jimmy所在位置下方第一块板左端为起点到地面的最短时间，
和右端为起点到地面的最短时间。
这两个子问题在形式上和原问题是完全一致的。
将板子从上到下从1开始进行无重复的编号（越高的板子编号越小，高度相同的几块板子，哪块编号在前无所谓），
那么和上面练歌子问题相关的变量就只有板子的编号。

2.状态转移方程：
不妨认为Jimmy开始的位置是一个编号为0，长度为0的板子，
假设LeftMintTime(k)表示从k号板子左端到地面的最短时间，
RightMinTime(k)表示从k号板子右端到地面的最短时间，
①求板子k左端点到地面的最短时间的方法如下：
if(板子k左端正下方没有别的板子)
{
  if(板子k的高度h(k)大于Max)
	LeftMinTime(k) = ∞;
  else
	LeftMinTime(k) = h(k);
}
else if(板子k左端正下方的板子编号是m)
{
  LeftMinTime(k) = h(k) - h(m) +
	Min(LeftMinTime(m) + Lx(k) - Lx(m),
	  RightMinTime(m)+Rx(m)-Lx(k));
}
②求板子k右端点到地面的最短时间的方法参①

h(i)代表i号板子的高度，Lx(i)就代表i号板子左端点的横坐标，Rx(i)就代表i号板子右端点的横坐标。

不妨认为Jimmy开始的位置是从一个编号为0，长度为0的板子，那么整个问题就是要求
LeftMinTime(0)。

注意：输入数据中，板子并没有按高度排序，所以程序中一定要首先将板子排序

时间复杂度：
一共n个板子，每个左右两端的最小时间各算一次O(n)
找出板子一端到地面之间有那块板子，需要遍历板子O(n)
总的时间复杂度:O(n^2)

当前版本：1.0
作    者：Louris
完成日期：2017.08.30
*/

#include<iostream>
#include<algorithm>
#include<string>
#include<limits.h>
#define OK 1
#define ERROR 0
#define inf 0x3f3f3f3f
typedef int Status;
using namespace std;
struct Plank
{
	int Hight;
	int Left;
	int Right;
}Planks[1001];
long long RightMinTime[1001];
long long LeftMinTime[1001];
long long MAX;
bool Compare(Plank a, Plank b)
{
	return a.Hight > b.Hight;
}
int main()
{
	int T;
	while (cin >> T)
	{
		//cin >> T;
		for (int t = 1; t <= T; t++)
		{
			//数据输入
			int n;
			int x, y;
			cin >> n >> x >> y >> MAX;
			for (int i = 1; i <= n; i++)
			{
				cin >> Planks[i].Left >> Planks[i].Right >> Planks[i].Hight;
			}
			//高度排序处理
			sort(Planks + 1, Planks + n + 1, Compare);
			//动规
			for (int i = n; i >= 1; i--)
			{
				int j;
				//找出左侧正下方是否有板子
				for (j = i + 1; j <= n; j++)
				{
					if ((Planks[i].Hight >= Planks[j].Hight&&Planks[i].Hight - Planks[j].Hight <= MAX)
						&& (Planks[i].Left >= Planks[j].Left && Planks[i].Left <= Planks[j].Right))
					{
						LeftMinTime[i] = Planks[i].Hight - Planks[j].Hight
							+ min(LeftMinTime[j] + Planks[i].Left - Planks[j].Left,
								RightMinTime[j] + Planks[j].Right - Planks[i].Left);
						break; //找到正下方的距离最近的板子即可
					}
				}
				//左侧正下方没板子
				if (j == n + 1)
				{
					if (Planks[i].Hight > MAX)
					{
						LeftMinTime[i] = inf;
					}
					else
					{
						LeftMinTime[i] = Planks[i].Hight;
					}
				}

				int k;
				//找出右侧正下方是否有板子
				for (k = i + 1; k <= n; k++)
				{
					if ((Planks[i].Hight >= Planks[k].Hight&&Planks[i].Hight - Planks[k].Hight <= MAX)
						&& (Planks[i].Right >= Planks[k].Left && Planks[i].Right <= Planks[k].Right))
					{
						RightMinTime[i] = Planks[i].Hight - Planks[k].Hight
							+ min(LeftMinTime[k] + Planks[i].Right - Planks[k].Left,
								RightMinTime[k] + Planks[k].Right - Planks[i].Right);
						break;
					}
				}
				//右侧正下方没板子
				if (k == n + 1)
				{
					if (Planks[i].Hight > MAX)
					{
						RightMinTime[i] = inf;
					}
					else
					{
						RightMinTime[i] = Planks[i].Hight;
					}
				}
			}
			int h;
			for (h = 1; h <= n; h++)
			{
				if ((y >= Planks[h].Hight&&y - Planks[h].Hight <= MAX)
					&& (Planks[h].Left <= x&&Planks[h].Right >= x))
				{
					LeftMinTime[0] = y - Planks[h].Hight
						+ min(LeftMinTime[h] + x - Planks[h].Left,
							RightMinTime[h] + Planks[h].Right - x);
					break;
				}
			}
			if (h == n + 1)
			{
				LeftMinTime[0] = y; //题目保证有解
			}
			cout << LeftMinTime[0] << endl;
		}
	}
	return 0;
}

滑雪

描述
Michael喜欢滑雪百这并不奇怪，因为滑雪的确很刺激。可是为了获得速度，滑的区域必须向下倾斜，而且当你滑到坡底，你不得不再次走上坡或者等待升降机来载你。Michael想知道载一个区域中最长的滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
一个人可以从某个点滑向上下左右相邻四个点之一，当且仅当高度减小。在上面的例子中，一条可滑行的滑坡为24-17-16-1。当然25-24-23-…-3-2-1更长。事实上，这是最长的一条。
输入
输入的第一行表示区域的行数R和列数C(1 <= R,C <= 100)。下面是R行，每行有C个整数，代表高度h，0<=h<=10000。
输出
输出最长区域的长度。
样例输入
5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
样例输出
25
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：滑雪.cpp

解题思路：
1.最优子结构：
①“每个点寻找其相邻的高度低于其高度且高度差最小的点
每个点计算完后，输出其中最大值即可”
无法求得，高度差最小的临近点的L值未必最大
②“每个点寻找临近的L值最大的点”

2.状态转移方程
L(i,j)表示从点(i,j)出发的最长滑行长度。
一个点(i,j)，如果周围没有比它低的点，L(i,j)=1
否则，
递推公式：
L(i,j)等于(i,j)周围四个点中，比(i,j)低，且L值最大的那个点的L值，再加1
复杂度：O(n^2)

将所有点按高度从小到大排序。每个点L值都初始化为1

从小到大遍历所有的点。经过一个点(i,j)时，递推求得即可

当前版本：1.0
作    者：Louris
完成日期：2017.08.31
*/

#include<iostream>
#include<algorithm>
using namespace std;
struct Point
{
	int row;
	int line;
	int hight;
}Points[10001];
int L[101][101];
int H[101][101];
bool compare(Point a, Point b)
{
	return a.hight < b.hight;
}
int main()
{
	int R, C;
	while (cin >> R >> C)
	{
		//L数组初始化
		for (int i = 0; i <= 101; i++)
		{
			fill(L[i], L[i] + 101, 1);
		}
		int j = 1;
		for (int row = 1; row <= R; row++)
		{
			for (int line = 1; line <= C; line++)
			{
				int hight;
				cin >> hight;
				H[row][line] = hight;
				Points[j].row = row;
				Points[j].line = line;
				Points[j].hight = hight;
				j++;
			}
		}
		//各点按高度排序
		sort(Points + 1, Points + j, compare);
		//动规
		for (int i = 1; i < j; i++)
		{
			int Max = 0;
			if (Points[i].row - 1 >= 1 && Points[i].hight > H[Points[i].row - 1][Points[i].line]) //上
			{
				Max = max(Max, L[Points[i].row-1][Points[i].line]);
			}
			if (Points[i].row + 1 <= R&&Points[i].hight > H[Points[i].row + 1][Points[i].line]) //下
			{
				Max = max(Max, L[Points[i].row + 1][Points[i].line]);
			}
			if (Points[i].line - 1 >= 1 && Points[i].hight > H[Points[i].row][Points[i].line - 1]) //左
			{
				Max = max(Max, L[Points[i].row][Points[i].line - 1]);
			}
			if (Points[i].line + 1 <= C && Points[i].hight > H[Points[i].row][Points[i].line + 1]) //右
			{
				Max = max(Max, L[Points[i].row][Points[i].line + 1]);
			}
			L[Points[i].row][Points[i].line] = max(L[Points[i].row][Points[i].line], Max + 1);
		}
		int MAX = 0;
		for (int i = 1; i <= R; i++)
		{
			for (int k = 1; k <= C; k++)
			{
				if (L[i][k] > MAX)
				{
					MAX = L[i][k];
				}
			}
		}
		cout << MAX << endl;
	}
	return 0;
}

神奇的口袋

描述
有一个神奇的口袋，总的容积是40，用这个口袋可以变出一些物品，这些物品的总体积必须是40。John现在有n个想要得到的物品，每个物品的体积分别是a1，a2……an。John可以从这些物品中选择一些，如果选出的物体的总体积是40，那么利用这个神奇的口袋，John就可以得到这些物品。现在的问题是，John有多少种不同的选择物品的方式。
输入
输入的第一行是正整数n (1 <= n <= 20)，表示不同的物品的数目。接下来的n行，每行有一个1到40之间的正整数，分别给出a1，a2……an的值。
输出
输出不同的选择物品的方式的数目。
样例输入
3
20
20
20
样例输出
3
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：神奇的口袋.cpp

解题思路：
设w体积，k种物品，则：
边界条件：
if(w==0) return 1;
if(k<=0) return 0;

总数=选第k种物品+不选第k中物品
Ways(w,k)=Ways(w,k-1)+Ways(w-a[k],k-1)

AC时间：50ms

当前版本：1.0
作    者：Louris
完成日期：2017.08.31
*/
#include<iostream>
using namespace std;
int a[30];
int N;
int Ways(int w, int k)
{
	if (w == 0)
	{
		return 1;
	}
	if (k <= 0)
	{
		return 0;
	}
	return Ways(w, k - 1) + Ways(w - a[k], k - 1);
}
int main()
{
	cin >> N;
	for (int i = 1; i <= N; i++)
	{
		cin >> a[i];
	}
	cout << Ways(40, N);
	return 0;
}

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：神奇的口袋_动规版.cpp

解题思路：
设w体积，k种物品，则：
边界条件：
if(w==0) return 1;
if(k<=0) return 0;

总数=选第k种物品+不选第k中物品
Ways(w,k)=Ways(w,k-1)+Ways(w-a[k],k-1)

AC时间:0ms

当前版本：1.0
作    者：Louris
完成日期：2017.08.31
*/
#include<iostream>
using namespace std;
int a[21];
int Ways[41][21];
int main()
{
	int n;
	while (cin >> n)
	{
		for (int i = 1; i <= n; i++)
		{
			cin >> a[i];
			Ways[0][i] = 1; //边界条件
		}
		//边界条件
		Ways[0][0] = 1;
		for (int i = 1; i <= 40; i++)
		{
			Ways[i][0] = 0;
		}
		//动规
		for (int i = 1; i <= 40; i++)
		{
			for (int j = 1; j <= n; j++)
			{
				if (i - a[j] < 0)
				{
					Ways[i][j] = Ways[i][j - 1];
				}
				else
				{
					Ways[i][j] = Ways[i][j - 1] + Ways[i - a[j]][j - 1];
				}
			}
		}
		cout << Ways[40][n] << endl;
	}
	return 0;
}

Charm Bracelet

描述
Bessie has gone to the mall’s jewelry store and spies a charm bracelet. Of course, she’d like to fill it with the best charms possible from the N(1 ≤ N≤ 3,402) available charms. Each charm iin the supplied list has a weight Wi(1 ≤ Wi≤ 400), a ‘desirability’ factor Di(1 ≤ Di≤ 100), and can be used at most once. Bessie can only support a charm bracelet whose weight is no more than M(1 ≤ M≤ 12,880).

Given that weight limit as a constraint and a list of the charms with their weights and desirability rating, deduce the maximum possible sum of ratings.
输入
Line 1: Two space-separated integers: N and M
Lines 2..N+1: Line i+1 describes charm i with two space-separated integers: Wi and Di
输出
Line 1: A single integer that is the greatest sum of charm desirabilities that can be achieved given the weight constraints
样例输入
4 6
1 4
2 6
3 12
2 7
样例输出
23
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：0-1背包问题.cpp

解题思路：
与上一题不同，此题背包未必装满。
用F[i][j]表示取前i种物品，使它们总体积不超过j的最优取法取得的价值总和。
要求F[N][M]

边界：
if(w[1]<=j)
  F[1][j]=d[1];
else
  F[1][j]=0;

递推：
f[i][j]=max(F[i-1][j],f[i-1][j-w[i]]+d[i])
取或不取第i种物品，两者选优
(j-w[i]>=0才有第二项)

本题如用记忆性递归，需要一个很大的二维数组，会超内存。注意到这个二维数组的下一行的值，
只用到了上一行的正上方及左边的值，因此可用滚动数组的思想，只要一行即可。即可以用一位数组，
用“人人为我”递推型动规实现。

空间优化分析：
求第i行j列的元素，按照状态转移方程可知，必须用到其上一行正上方的元素和该元素左侧的一个元素
①行分析：
那么按照行从小到大的顺序进行，当前行各元素计算完成则其上一行元素失去作用，不再参与计算，
故可以将下一行的各元素的计算结果保存到上一行，已达到空间优化的目的。
②列分析：
由于当前元素的计算需要其正上方及其左边的某个元素，那么，
如果从左到右进行枚举，当前元素的计算结果保存到其正上方元素，则进行右边的其他元素时
可能会用到这个已经被保存计算结果的元素，所以不可以。
如果从右到左进行枚举，当前元素的计算结果保存到其正上方元素，对当行左边其他元素的计算不产生任何影响
故达到了空间优化的目的。
综上：采用从上到下，从右到左的顺序进行枚举。

当前版本：1.0
作    者：Louris
完成日期：2017.08.31
*/
#include<iostream>
#include<algorithm>
using namespace std;
struct Goods
{
	int Value;
	int Volume;
}goods[3501];
int Gross[13001];
int N, M;
int main()
{
	while (cin >> N >> M)
	{
		for (int i = 1; i <= N; i++)
		{
			cin >> goods[i].Volume >> goods[i].Value;
		}
		//边界条件
		for (int j = 1; j <= M; j++)
		{
			if (goods[1].Volume <= j)
			{
				Gross[j] = goods[1].Value;
			}
			else
			{
				Gross[j] = 0;
			}
		}
		Gross[0] = 0;
		//动规 f[i][j]=max(F[i-1][j],f[i-1][j-w[i]]+d[i])
		for (int i = 2; i <= N; i++)
		{
			for (int j = M; j >= 1; j--)
			{
				if (j >= goods[i].Volume)
				{
					Gross[j] = max(Gross[j], Gross[j-goods[i].Volume] + goods[i].Value);
				}
			}
		}
		cout << Gross[M] << endl;
	}
	return 0;
}

分蛋糕

描述
有一块矩形大蛋糕，长和宽分别是整数w 、h。现要将其切成m块小蛋糕，每个小蛋糕都必须是矩形、且长和宽均为整数。切蛋糕时，每次切一块蛋糕，将其分成两个矩形蛋糕。请计算：最后得到的m块小蛋糕中，最大的那块蛋糕的面积下限。
输入
共有多行，每行表示一个测试案例。每行是三个用空格分开的整数w, h, m ，其中1 ≤ w, h, m ≤ 20 ， m ≤ wh. 当 w = h = m = 0 时不需要处理，表示输入结束。
输出
每个测试案例的结果占一行，输出一个整数，表示最大蛋糕块的面积下限。
样例输入
4 4 4
4 4 3
0 0 0
样例输出
4
6
程序

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int INFI = 0xffffff;
int W, H, M;
int minMax[30][30][410];
int Dfs(int w, int h, int m)
{
	if (w*h < m + 1)
		return INFI;
	if (m == 0)
		return w*h;
	if (minMax[w][h][m] != -1)
		return minMax[w][h][m];
	int mx = INFI;
	for (int i = 1; i <= w - 1; i++)
	{
		for (int k = 0; k <= m - 1; k++)
		{
			int m1 = Dfs(i, h, k);
			int m2 = Dfs(w - i, h, m - 1 - k);
			mx = min(mx, max(m1, m2));
		}
	}
	for (int i = 1; i <= h - 1; i++)
	{
		int m1, m2;
		for (int k = 0; k <= m - 1; k++)
		{
			m1 = Dfs(w, i, k);
			m2 = Dfs(w, h - i, m - 1 - k);
			mx = min(mx, max(m1, m2));
		}
	}
	minMax[w][h][m] = mx;
	return mx;
}
int main()
{
	while (true)
	{
		cin >> W >> H >> M;
		if (W == 0 && H == 0)
			break;
		memset(minMax, 0xff, sizeof(minMax));
		cout << Dfs(W, H, M - 1) << endl;
	}
	return 0;
}

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：分蛋糕.cpp

解题思路：
设Ways(w,h,m)表示宽为w，高为h的蛋糕，被切m刀后，最大的那块蛋糕的面积最小值。
题目就是求Ways(W,H,M-1)

边界条件：
一块宽w，高h的蛋糕，最多能切
  w - 1
	+
 w * (h - 1)
= w * h - 1刀：

  判断条件      面积
w * h - 1 < m    inf
   m == 0       w * h

递推式：
SV为第一刀竖着切时能得到的最好结果，SH为第一刀横着切时能得到的最好结果，
则Ways(w,h,m) = min(SV,SH)

SV = min{ Si,i = 1, ... ,w-1 }，其中，Si = 第一刀后左边宽为i的情况下的最好结果
Si = min{ max(ways(i,h,k), ways(w-i,h,m-1-k)),k=0, ... ,m-1 }

SH = min{ Sj,j=1, ... ,h-1 }，其中，Sj = 第一刀后左边高位j的情况下的最好结果
Sj = min{ max(ways(w,j,k), ways(w,h-j,m-1-k)),k=0, ... ,m-1 }

当前版本：1.0
作    者：Louris
完成日期：2017.09.01
*/

#include<iostream>
#include<algorithm>
using namespace std;
const int inf = 0xffffff;
int W, H, M;
int Ways[21][21][21];
int main()
{
	while (cin >> W >> H >> M&&W != 0 && H != 0 && M != 0)
	{
		//边界条件
		for (int w = 1; w <= W; w++)
		{
			for (int h = 1; h <= H; h++)
			{
				Ways[w][h][0] = w*h;
			}
		}
		//动规
		for (int h = 1; h <= H; h++)
		{
			for (int w = 1; w <= W; w++)
			{

				for (int m = 1; m < M; m++)
				{
					if (w*h - 1 < m)
					{
						Ways[w][h][m] = inf;
						continue;
					}
					//枚举第一刀竖着切
					int SV = inf;
					for (int i = 1; i < w; i++)
					{
						for (int k = 0; k < m; k++)
						{
							SV = min(SV, max(Ways[i][h][k], Ways[w - i][h][m - 1 - k]));
						}
					}

					//枚举第一刀横着切
					int SH = inf;
					for (int j = 1; j < h; j++)
					{
						for (int k = 0; k < m; k++)
						{
							SH = min(SH, max(Ways[w][j][k], Ways[w][h - j][m - 1 - k]));
						}
					}

					Ways[w][h][m] = min(SV, SH);

				}
			}
		}
		cout<<Ways[W][H][M-1]<<endl;
	}
	return 0;
}

复杂的整数划分问题

描述
将正整数n 表示成一系列正整数之和，n=n1+n2+…+nk, 其中n1>=n2>=…>=nk>=1 ，k>=1 。
正整数n 的这种表示称为正整数n 的划分。
输入
标准的输入包含若干组测试数据。每组测试数据是一行输入数据,包括两个整数N 和 K。
(0 < N <= 50, 0 < K <= N)
输出
对于每组测试数据，输出以下三行数据:
第一行: N划分成K个正整数之和的划分数目
第二行: N划分成若干个不同正整数之和的划分数目
第三行: N划分成若干个奇正整数之和的划分数目
样例输入
5 2
样例输出
2
3
3
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：复杂的整数划分问题.cpp

解题思路：
1.最优子结构
①先随机划分一个数
②对在①的基础上的差进行划分
③重复①②直至求解完成

2.状态转移方程
①n划分成m个正整数之和的划分数目，即求：
设n的m划分的个数为f(n,m):
n的m划分 = n的m个划分至少为1，也就是说要么等于1 要么大于1，
那么问题就一分为二了：
n的m划分 = n的m划分一定包含1 + n的m划分中都大于1
f(n,m) = f(n-1,m-1)
if(n-m>=m)
  f(n,m) += f(n-m,m)
边界条件：
m>n f(n,m)=0
f(n,1)=1
f(n,0)=0
f(0,0)=1
②n划分成若干个不同正整数之和的划分数目,
设n的划分为f(n,m),m为当前划分出的最大数:
n的划分 = n划分出m + n不划分出m，即
if(n-m>=0)
  f(n,m)=f(n-m,m-1)+f(n,m-1)
else
  f(n,m)=f(n,m-1)
边界条件：
m≠0，f(0,m)=1 因为划分完了，且满足了递件要求
n≠0, f(n,0)=0 因为按照递减划分，那么最后必须要分完，且满足递减要求
f(0,0)=1 因为分完且满足了递减要求

③n划分成若干个奇正整数之和的划分数目：
设n的划分为f(n,m),m为当前划分出的最大数，且m为奇数:
n的划分 = n划分出m + n不划分出m，即
if(n-m>=0)
f(n,m)=f(n-m,m)+f(n,m-2)
else
f(n,m)=f(n,m-2)
边界条件：
m≠0，f(0,m)=1 因为划分完了
n>1,f(n,1)=0;
f(1,1)=1
f(5,5)=f(0,5)+f(5,3)=1+f(2,3)+f(5,1)=1+f(2,1)+f(5,1)=1+1+1=3
f(6,5)=f(1,5)+f(6,3)=1+f(3,3)+f(6,1)=1+f(0,3)+f(3,1)+1=1+1+1+1=4

当前版本：1.0
作    者：Louris
完成日期：2017.09.02
*/
#include<iostream>
#include<algorithm>
using namespace std;
int Sum[51][51];
int main()
{
	int n, k;
	while (cin >> n >> k)
	{
		//第一问
		//边界条件
		for (int i = 1; i <= n; i++)
		{
			Sum[i][1] = 1;
			Sum[i][0] = 0;
		}
		Sum[0][0] = 1;
		//动规
		for (int i = 1; i <= n; i++)
		{
			for (int j = 1; j <= k; j++)
			{
				if (i < j)
				{
					Sum[i][j] = 0;
					continue;
				}
				Sum[i][j] = Sum[i - 1][j - 1];
				if (i - j >= j)
				{
					Sum[i][j] += Sum[i - j][j];
				}

			}
		}
		cout << Sum[n][k] << endl;

		//第二问
		//边界条件
		for (int i = 1; i <= n; i++)
		{
			Sum[i][0] = 0;
			Sum[0][i] = 1;
		}
		Sum[0][0] = 1;
		//动规
		for (int i = 1; i <= n; i++)
		{
			for (int j = 1; j <= n; j++)
			{
				if (i - j >= 0)
				{
					Sum[i][j] = Sum[i - j][j - 1] + Sum[i][j - 1];
				}
				else
				{
					Sum[i][j] = Sum[i][j - 1];
				}
			}
		}
		cout << Sum[n][n] << endl;

		//第三问
		for (int i = 0; i <= n; i++)
		{
			Sum[0][i] = 1;
			Sum[i][1] = 1;
		}
		//动规
		for (int i = 1; i <= n; i++)
		{
			for (int j = 3; j <= n; j+=2)
			{
				if (i - j >= 0)
				{
					Sum[i][j] = Sum[i - j][j] + Sum[i][j - 2];
				}
				else
				{
					Sum[i][j] = Sum[i][j - 2];
				}
			}
		}
		if (n % 2 == 0)
		{
			cout << Sum[n][n - 1] << endl;
		}
		else
		{
			cout << Sum[n][n] << endl;
		}
	}
	return 0;
}

Blocks

描述
Some of you may have played a game called ‘Blocks’. There are n blocks in a row, each box has a color. Here is an example: Gold, Silver, Silver, Silver, Silver, Bronze, Bronze, Bronze, Gold. The corresponding picture will be as shown below:
Blccks图示
If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a ‘box segment’. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1 box(es) in the segments respectively.

Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get kk points. for example, if you click on a silver box, the silver segment disappears, you got 44=16 points.

Now let’s look at the picture below: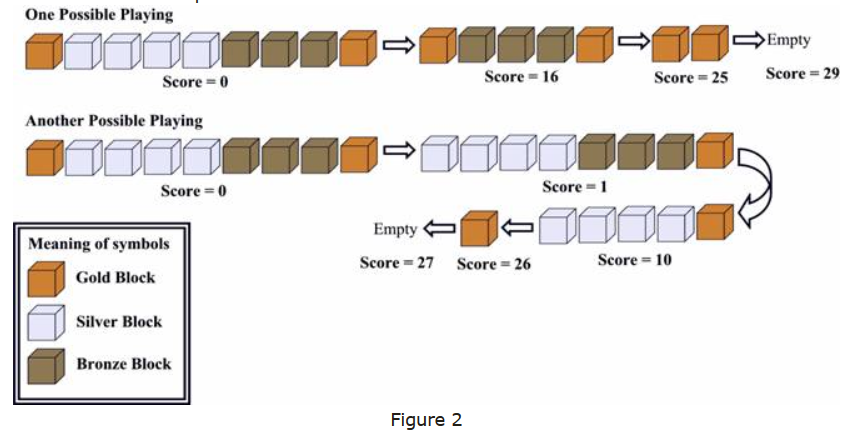
Blccks图示
The first one is OPTIMAL.

Find the highest score you can get, given an initial state of this game.
输入
The first line contains the number of tests t(1<=t<=15). Each case contains two lines. The first line contains an integer n(1<=n<=200), the number of boxes. The second line contains n integers, representing the colors of each box. The integers are in the range 1~n.
输出
For each test case, print the case number and the highest possible score.
样例输入
2
9
1 2 2 2 2 3 3 3 1
1
1
样例输出
Case 1: 29
Case 2: 1
程序

/*

文件名称：Blocks.cpp

解题思路：
①同种颜色的方盒被点击的次数越少，玩家获得的积分越高
②明显的递归问题：
每次点击之后，剩下的方盒构成一个新的方盒队列，新队列中方盒的数量减少了，
然后计算玩家从新队列中可获得的最高积分。

将连续的若干个方块作为一个“大块”(box_segment)考虑，假设开始一共有n个
“大块”，编号0 - n-1
第i个大块的颜色是color[i]，
包含的方块数目，即长度，是len[i]
用click_box(i,j)表示从大块i到大块j这一段消除后的所得的最高分
则整个问题就是：click_box(0,n-1)

要求click_box(i,j)时，考虑最右边的大块j，对它有两种处理方式，
要取其优者：
①直接消除它，此时能得到的最高分就是：
click_box(i,j-1)+len[j]*len[j]
②期待以后它能和左边的某个同色大块合并
考虑和左边的某个同色大块合并：
左边的同色大块可能有很多歌，到底和哪个合并最好，不知道，只能枚举。
假设大块j和左边的大块看、
(i<=k<j-1)合并，此时能得到的最高分是多少呢？
是不是：
click_box(i,k-1)+click_box(k+1,j-1)+(len[k]+len[j])^2
不对！
因为将大块k和大块j合并后，形成的新大块会在最右边。将该新大块直接将其消去的做法，
才符合上述式子，但直接将其消去，未必是最好的，也许它还应该和左边的同色大块合并才更好。

递推关系无法形成，怎么办？
需要改变问题的形式，
click_box(i,j)这个形式不可取，因为无法形成递推关系
考虑新的形式：
click_box(i,j,ex_len)
表示：
大块j的右边已经有一个长度为ex_len的大块(该大块可能是在合并过程中形成的，
不妨称其为ex_len)，且j的颜色和ex_len相同，在此情况下将i到j以及ex_len都消除
所能得到的最高分。

于是整个问题就是求：
click_box(0,n-1,0)
求click_box(i,j,ex_len)时，有两种处理方法，取最优者
假设j和ex_len合并后的大块称作Q
①将Q直接消除，这种做法能得到的最高分就是：
click_box(i,j-1,0)+(len[j]+ex_len)^2
②期待Q以后能和左边的某个同色大块合并。需要枚举可能和Q合并的大块。
假设让大块k和Q合并，则此时能得到的最大分数是：
click_box(i,k,len[j]+ex_len)+click_box(k+1,j-1,0)

递归的终止条件是什么？
click_box(i,j,ex_len)递归终止条件：
i==j

完成日期：2017.09.15
*/
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int M = 210;
struct Segment
{
	int color;
	int len;
}segments[M];
int score[M][M][M];
int ClickBox(int i, int j, int len)
{
	if (score[i][j][len] != -1)//剪枝
	{
		return score[i][j][len];
	}
	int result = (segments[j].len + len)*(segments[j].len + len); //直接消去
	if (i == j)
	{
		return result;
	}
	result += ClickBox(i, j - 1, 0);//直接消去
	for (int k = i; k <= j - 1; k++)
	{
		if (segments[k].color != segments[j].color)
		{
			continue;
		}
		int r = ClickBox(k + 1, j - 1, 0);
		r += ClickBox(i, k, segments[j].len + len);//和某个大块合并
		result = max(result, r);//取最高分
	}
	score[i][j][len] = result;
	return result;
}
int main()
{
	int T;
	cin >> T;
	for (int t = 1; t <= T; t++)
	{
		int n;
		memset(score, 0xff, sizeof(score));
		cout << score[1][1][1] << endl;
		cin >> n;
		int lastC = 0;
		int segNum = -1;
		for (int i = 0; i < n; i++)
		{
			int c;
			cin >> c;
			if (c != lastC)
			{
				segNum++;
				segments[segNum].len = 1;
				segments[segNum].color = c;
				lastC = c;
			}
			else
			{
				segments[segNum].len++;
			}
		}
		//边界条件
		cout << "Case " << t << ": " << ClickBox(0, segNum, 0) << endl;
	}
	return 0;
}

Dividing the path

描述
Farmer John’s cows have discovered that the clover growing along the ridge of the hill in his field is particularly good. To keep the clover watered, Farmer John is installing water sprinklers along the ridge of the hill.

To make installation easier, each sprinkler head must be installed along the ridge of the hill (which we can think of as a one-dimensional number line of length L (1 <= L <= 1,000,000); L is even).

Each sprinkler waters the ground along the ridge for some distance in both directions. Each spray radius is an integer in the range A..B (1 <= A <= B <= 1000). Farmer John needs to water the entire ridge in a manner that covers each location on the ridge by exactly one sprinkler head. Furthermore, FJ will not water past the end of the ridge in either direction.

Each of Farmer John’s N (1 <= N <= 1000) cows has a range of clover that she particularly likes (these ranges might overlap). The ranges are defined by a closed interval (S,E). Each of the cow’s preferred ranges must be watered by a single sprinkler, which might or might not spray beyond the given range.

Find the minimum number of sprinklers required to water the entire ridge without overlap.
输入
Line 1: Two space-separated integers: N and L
Line 2: Two space-separated integers: A and B
Lines 3..N+2: Each line contains two integers, S and E (0 <= S < E <= L) specifying the start end location respectively of a range preferred by some cow. Locations are given as distance from the start of the ridge and so are in the range 0..L.
输出
Line 1: The minimum number of sprinklers required. If it is not possible to design a sprinkler head configuration for Farmer John, output -1.
样例输入
2 8
1 2
6 7
3 6
样例输出
3
程序

/*

文件名称：Dividing_the_Path.cpp

解题思路：
从线段的起点向终点安装喷水头，令f(x)表示：所安装喷水头的喷洒范围恰好
覆盖直线上的区间[0,x]时，最少需要多少个喷水头。
显然，x应满足下列条件：
①x为偶数
②x所在位置不会出现奶牛，即x不属于任何一个(S,E)
③x≥2A
④当x>2B时，存在Y∈[x-2B,x-2A]且Y满足上述三个条件，使得f(x)=f(y)+1

递推计算f(x):
①f(x)=∞：x是奇数 √
②f(x)=∞：x<2A √
③f(x)=∞：x处可能有奶牛触摸  √
④f(x)=1：2A≤x≤2B、且x位于任何奶牛的活动范围之外  √
⑤f(x)=1+min{f(y)：y∈[x-2B,x-2A]、Y位于任何奶牛的活动范围之外}：x>2B √

1.对每个x求f(x)，都要遍历区间[x-2B,x-2A]去寻找其中最小的f(y)，则时间复杂度为：
L*B=1000000*1000，太慢

2.快速找到[x-2B,x-2A]中使得f(y)最小的元素是问题求解速度的关键。

3.可以使用优先队列priority_queue!(multiset也可以，比priority_queue慢一点！)

4.求f(x)时，若坐标属于[x-2B,x-2A]的二元组(i,f(i))都保存在一个priority_queue中
并根据f(i)值排序，则队头元素就能确保是f(i)值最小的。

5.在求x点的f(x)时，必须确保队列中包含所有属于[x-2B,x-2A]的点。
而且，不允许出现坐标大于x-2A的点，因为这样的点对求f(x)无用，如果这样的点
出现在队头，因其对求后续点的f值有用，故不能抛弃，于是算法就无法继续了。

6.队列中可以出现坐标小于x-2B的点。这样的点若出现在队头，则直接将其抛弃。√

7.求出x点的f值后，将(x-2A+2,f(x-2A+2))放入队列，为求f(x+2)作准备。√

8.队列里只要存坐标为偶数的点即可。

完成日期：2017.09.16
*/
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int INFINITE = 1 << 30;
const int MAXL = 1000010;
const int MAXN = 1010;
int F[MAXL]; //F[L]就是答案
int cowThere[MAXL]; //cowThere[i]为1表示点i有奶牛
int N, L, A, B;
struct Fx
{
	int x;
	int f;
	bool operator < (const Fx &a)const
	{
		return f > a.f;
	}
	Fx(int xx = 0, int ff = 0) :x(xx), f(ff){}
}; //在优先队列里，f值越小越优先
priority_queue<Fx>qFx;
int main()
{
	cin >> N >> L;
	cin >> A >> B;
	A <<= 1; //A，B的定义变为覆盖的直径
	B <<= 1;
	memset(cowThere, 0, sizeof(cowThere));
	for (int i = 0; i < N; i++)
	{
		int s, e;
		cin >> s >> e;
		//以下区间表示避免同一区间同一头牛重复统计，那么以区间开头记录，结尾删除记录
		++cowThere[s + 1]; //从s+1起进入一个奶牛区
		--cowThere[e]; //从e起退出一个奶牛区
	}
	int inCows = 0; //表示当前点位于多少头奶牛的活动范围之内
	for (int i = 0; i <= L; i++) //算出每个点是否有奶牛
	{
		F[i] = INFINITE;
		inCows += cowThere[i]; //以上输入每头牛的活动区间时会有正有负，表示当前点是否奶牛，避免了重复统计，甚是巧妙！
		cowThere[i] = inCows > 0;
	}
	for (int i = A; i <= B; i += 2) //初始化队列
	{
		if (!cowThere[i]) //没牛在喷洒器的边界上！
		{
			F[i] = 1;
			if (i <= B + 2 - A) //求F[i]的时候，要确保队列里的点x，x<=i-A (y≤x-A) √ 为求x=B+2做准备
			{
				qFx.push(Fx(i, 1));
			}
		}
	}
	//动规
	for (int i = B + 2; i <= L; i += 2)
	{
		if (!cowThere[i])  //√
		{
			Fx fx;
			while (!qFx.empty())  //√
			{
				fx = qFx.top();
				if (fx.x < i - B)
				{
					qFx.pop();
				}
				else
				{
					break;
				}
			}
			if (!qFx.empty()) //√
			{
				F[i] = fx.f + 1;
			}
		}
		if (F[i - A + 2] != INFINITE)  //√
		{
			qFx.push(Fx(i - A + 2, F[i - A + 2]));
		}
	}
	if (F[L] == INFINITE)
	{
		cout << -1 << endl;
	}
	else
	{
		cout << F[L] << endl;
	}
	return 0;
} //复杂度：O(nlogn)

第五章深度优先搜索

深度优先遍历图的方法

从图中某顶点V触发：
（1）访问顶点V；
（2）依次从V的未被访问的邻接点触发，对图进行深度优先遍历；直至图中和V有路径相通的顶点都被访问；
（3）若此时图中尚有顶点未被访问，则从一个未被访问的顶点触发，重新进行深度优先遍历，直到图中所有点均被访问过为止。

bool Dfs(V) //判断从V能否走到终点
{
  if(V为终点)
    return true;
  if(V为旧点)
    return false;
    将V标记为旧点;
    对和V相邻的每个节点U
    {
      if(Dfs(U)==true)
        return true;
    }
    return false;
}
int main()
{
  将所有点标记为新点；
  起点=1
  终点=8
  cout<<Dfs(V)<<endl;
  return 0;
}

判断从V出发释放后能走到终点，如果能，要记录路径

Node path[MAX_LEN]; //MAX_LEN取节点总数即可
int depth;
bool Dfs(V)
{
  if(V为终点)
  {
    path[depth]=V;
    return true;
  }
  if(V为旧点)
  {
    return false;
  }
  将V标记为旧点;
  path[depth]=V;
  ++depth;
  对和V相邻的每个结点U
  {
    if(Dfs(U)==true)
    {
      return true;
    }
  }
  --depth;
  return false;
}
int main()
{
  将所有点都标记为新点;
  depth=0;
  //连通，非连通图需要加一层循环
  if(Dfs(起点))
  {
    for(int i=0;i<=depth;i++)
    {
      cout<<path[i]<<endl;
    }
  }
}

遍历涂上所有节点

Dfs(V)
{
  if(V是旧点)
  {
    return;
  }
  将V标记为旧点;
  对和V相邻的每个点U
  {
    Dfs(U);
  }
}
int main()
{
  将所有点都标记为新点;
  while(在途中能找到新点k)
  {
    Dfs(k);
  }
}

图的表示方法

a.邻接矩阵
用一个二维数组G存放图，G[i][j]表示节点i和节点j之间边的情况（如有无边，边方向，权值大小等）
遍历复杂度：O(n^2) n为节点数目
b.每个节点V对应一个一位数组(vector)，里面存放从V连出去的边，边的信息包括另一个顶点，还可能包含边权值等。
遍历复杂度：O(n+e) n为节点数目，e为边数目

注：详见数据结构/图

城堡问题

描述

1   2   3   4   5   6   7  
#############################
1 #   |   #   |   #   |   |   #
#####---#####---#---#####---#
2 #   #   |   #   #   #   #   #
#---#####---#####---#####---#
3 #   |   |   #   #   #   #   #
#---#########---#####---#---#
4 #   #   |   |   |   |   #   #
#############################
      (图 1)
#  = Wall   
|  = No wall
-  = No wall

图1是一个城堡的地形图。请你编写一个程序，计算城堡一共有多少房间，最大的房间有多大。城堡被分割成m × n (m≤50，n≤50)个方块，每个方块可以有0~4面墙。
输入
程序从标准输入设备读入数据。第一行是两个整数，分别是南北向、东西向的方块数。在接下来的输入行里，每个方块用一个数字(0≤p≤50)描述。用一个数字表示方块周围的墙，1表示西墙，2表示北墙，4表示东墙，8表示南墙。每个方块用代表其周围墙的数字之和表示。城堡的内墙被计算两次，方块(1,1)的南墙同时也是方块(2,1)的北墙。输入的数据保证城堡至少有两个房间。
输出
城堡的房间数、城堡中最大房间所包括的方块数。结果显示在标准输出设备上。
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：城堡问题.cpp

解题思路：
1.把方块看作是节点，相邻两个方块之间如果没有墙，则在方块之间连一条边，这样城堡就能转换成一个图。

2.求房间个数，实际上就是在求图中有多少个极大连通子图。

3.一个连通子图，往里头加任何一个图里的其他点，就会变得不连通，那么这个连通子图就是极大连通子图。

4.对每一个房间，深度优先搜索，从而给这个房间能够到达的所有位置染色。最后统计一共用了几种颜色，
以及每种颜色的数量。

当前版本：1.0
作    者：Louris
完成日期：2017.09.05
*/
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define OK 1
#define ERROR 0
typedef int Status;
int R, C; //行列数
int rooms[60][60];
int color[60][60];
int maxRoomArea = 0, roomNum = 0;
int roomArea;
Status Dfs(int i, int k)
{
	if (color[i][k]) //保证新点
	{
		return OK;
	}
	++roomArea;
	color[i][k] = roomNum;
	if ((rooms[i][k] & 1) == 0)  //机智，我说为什么那么特殊，1,2,4,8位运算二进制表示刚好1111
	{
		Dfs(i, k - 1);//向西走
	}
	if ((rooms[i][k] & 2) == 0)
	{
		Dfs(i - 1, k);//向北
	}
	if ((rooms[i][k] & 4) == 0)
	{
		Dfs(i, k + 1);//向东
	}
	if ((rooms[i][k] & 8) == 0)
	{
		Dfs(i + 1, k);//向南
	}
}
int main()
{
	cin >> R >> C;
	for (int i = 1; i <= R; ++i)
	{
		for (int k = 1; k <= C; ++k)
		{
			cin >> rooms[i][k];
		}
	}
	memset(color, 0, sizeof(color));
	for (int i = 1; i <= R; i++)
	{
		for (int k = 1; k <= C; k++)
		{
			if (!color[i][k])
			{
				++roomNum;
				roomArea = 0;
				Dfs(i, k);
				maxRoomArea = max(roomArea, maxRoomArea);
			}
		}
	}
	cout << roomNum << endl;
	cout << maxRoomArea << endl;
	return 0;
}

踩方格

描述
有一个方格矩阵，矩阵边界在无穷远处。我们做如下假设：
a.每走一步时，只能从当前方格移动一格，走到某个相邻的方格上；
b.走过的格子立即塌陷无法再走第二次；
c.只能向北、东、西三个方向走；
请问：如果允许在方格矩阵上走n步，共有多少种不同的方案。2种走法只要有一步不一样，即被认为是不同的方案。
输入
允许在方格上行走的步数n(n <= 20)
输出
计算出的方案数量
样例输入
2
样例输出
7
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：踩方格.cpp

解题思路：
递归：
从(i,j)出发，走n步的方案数，等于以下三项之和：
从(i+1,j)出发，走n-1步的方案数。前提：(i+1,j)还没走过
从(i,j+1)出发，走n-1步的方案数。前提：(i,j+1)还没走过
从(i,j-1)出发，走n-1步的方案数。前提：(i,j-1)还没走过

当前版本：1.0
作    者：Louris
完成日期：2017.09.05
*/
#include<iostream>
#include<cstring>
using namespace std;
int visited[30][50];
int ways(int i, int j, int n)
{
	if (n == 0)
	{
		return 1;
	}
	visited[i][j] = 1;
	int num = 0;
	if (!visited[i][j - 1])
	{
		num += ways(i, j - 1, n - 1);
	}
	if (!visited[i][j + 1])
	{
		num += ways(i, j + 1, n - 1);
	}
	if (!visited[i+1][j ])
	{
		num += ways(i + 1, j, n - 1);
	}
	visited[i][j] = 0; //复位
	return num;
}
int main()
{
	int n;
	cin >> n;
	memset(visited, 0, sizeof(visited));
	cout << ways(0, 25, n) << endl;
	return 0;
}

ROADS

描述
N cities named with numbers 1 … N are connected with one-way roads. Each road has two parameters associated with it : the road length and the toll that needs to be paid for the road (expressed in the number of coins).
Bob and Alice used to live in the city 1. After noticing that Alice was cheating in the card game they liked to play, Bob broke up with her and decided to move away - to the city N. He wants to get there as quickly as possible, but he is short on cash.
We want to help Bob to find the shortest path from the city 1 to the city N that he can afford with the amount of money he has.
输入
The first line of the input contains the integer K, 0 <= K <= 10000, maximum number of coins that Bob can spend on his way.
The second line contains the integer N, 2 <= N <= 100, the total number of cities.
The third line contains the integer R, 1 <= R <= 10000, the total number of roads.
Each of the following R lines describes one road by specifying integers S, D, L and T separated by single blank characters :
S is the source city, 1 <= S <= N
D is the destination city, 1 <= D <= N
L is the road length, 1 <= L <= 100
T is the toll (expressed in the number of coins), 0 <= T <=100
Notice that different roads may have the same source and destination cities.
输出
The first and the only line of the output should contain the total length of the shortest path from the city 1 to the city N whose total toll is less than or equal K coins.
If such path does not exist, only number -1 should be written to the output.
样例输入
5
6
7
1 2 2 3
2 4 3 3
3 4 2 4
1 3 4 1
4 6 2 1
3 5 2 0
5 4 3 2
样例输出
11
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：ROADS.cpp

解题思路：
邻接表，递归，深度优先搜索

从城市1开始深度优先遍历整个图，找到所有能过到达N的走法。
选一个最优的。

最优性剪枝：
1）如果当前已经找到的最优路径长度为L，那么在继续搜索的过程中，总长度已经大于等于L的走法，就可以直接放弃，不用走到底了。

保存中间计算结果用于最优性剪枝：
2）用midL[k][m]表示：走到城市k时总过路费为m的条件下，最优路径的长度。
若在后续的搜索中，再次走到k时，如果总路费恰好为m，且此时的路径长度已经超过
midL[k][m]，则不必再走下去了。


当前版本：1.0
作    者：Louris
完成日期：2017.09.05
*/
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
#define OK 1
typedef int Status;
int K, N, R;
struct Road   //邻接表
{
	int dest;
	int length;
	int cost;
};
vector< vector<Road> > G(110);
int minLen;
int totalLen;
int totalCost;
int visited[110];
int midL[110][10010];//到达城市i的花费j
Status Dfs(int s)
{
	if (s == N)
	{
		minLen = min(minLen,totalLen);
		return OK;
	}
	for (unsigned int i = 0; i < G[s].size(); i++)
	{
		Road r = G[s][i];
		if (totalCost + r.cost > K)  //剪枝
		{
			continue;
		}
		if (!visited[r.dest])
		{
			if (totalLen + r.length >= minLen) //剪枝
			{
				continue;
			}
			if (totalLen + r.length >= midL[r.dest][totalCost + r.cost])//剪枝
			{
				continue;
			}
			midL[r.dest][totalCost + r.cost] = totalLen + r.length;
			totalLen += r.length;
			totalCost += r.cost;
			visited[r.dest] = 1;
			Dfs(r.dest);
			visited[r.dest] = 0;
			totalLen -= r.length;
			totalCost -= r.cost;
		}
	}
	return OK;
}

int main()
{
	cin >> K >> N >> R;
	for (int i = 1; i <= R; i++)
	{
		int s;
		Road r;
		cin >> s >> r.dest >> r.length >> r.cost;
		if (s != r.dest)
		{
			G[s].push_back(r);
		}
	}
	memset(visited, 0, sizeof(visited));
	totalLen = 0;
	minLen = 1 << 30;
	totalCost = 0;
	visited[1] = 1;
	for (int i = 0; i < 110; i++)
	{
		for (int j = 0; j < 10010; j++)
		{
			midL[i][j] = 1 << 30;
		}
	}
	Dfs(1);
	if (minLen < (1 << 30))
	{
		cout << minLen << endl;
	}
	else
	{
		cout << "-1" << endl;
	}
	return 0;
}

生日蛋糕

描述
7月17日是Mr.W的生日，ACM-THU为此要制作一个体积为Nπ的M层生日蛋糕，每层都是一个圆柱体。
设从下往上数第i(1 <= i<= M)层蛋糕是半径为Ri, 高度为Hi的圆柱。当i < M时，要求Ri > Ri+1且Hi > Hi+1。
由于要在蛋糕上抹奶油，为尽可能节约经费，我们希望蛋糕外表面（最下一层的下底面除外）的面积Q最小。
令Q = Sπ
请编程对给出的N和M，找出蛋糕的制作方案（适当的Ri和Hi的值），使S最小。
（除Q外，以上所有数据皆为正整数）
输入
有两行，第一行为N（N <= 10000），表示待制作的蛋糕的体积为Nπ；第二行为M(M <= 20)，表示蛋糕的层数为M。
输出
仅一行，是一个正整数S（若无解则S = 0）。
样例输入
100
2
样例输出
68
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：生日蛋糕.cpp

解题思路：
1.深度优先搜索，枚举每一层可能的高度和半径

2.如何确定搜索范围？
底层蛋糕的最大可能半径和最大可能高度

3.搜索顺序，哪些地方体现搜索顺序？
从底层往上搭，而不是从顶层往下搭

4.如何剪枝？
①最优性剪枝：
搭建过程中发现已建好的面积已经超过目前求得的最优表面积，
或者预见到搭完后面积一定会超过目前最优表面积，则停止搭建
②可行性（预测）剪枝：
a.搭建过程中预见到再往上搭，高度已经无法安排，
或者半径已经无法安排，则停止搭建。
b.搭建过程中发现还没搭的那些层的体积，一定会超过还缺的体积，则停止搭建。
c.搭建过程中发现还没搭的那些层的体积，最大也到不了还缺的体积，则停止搭建。
d.放缩剪枝
第k层时剩下第1到第k-1层的面积 2∑(i=1~k-1)*Ri*Hi > ∑(i=1~k-1)2*Ri*Ri*Hi / Rk
所以有当前面积S，剩余体积V，当前最优表面积
   S+2*V/Rk>A
可以剪枝

AC时耗;
未加放缩剪枝：28ms
加上放缩剪枝：9ms

当前版本：1.0
作    者：Louris
完成日期：2017.09.06
*/
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#define OK 1
#define ERROR 0
typedef int Status;
using namespace std;
int N, M;
int minArea = 1 << 30; //最优表面积
int area = 0; //正在搭建中的蛋糕的表面积
Status Dfs(int v, int n, int r, int h)
{
	//要用n层去凑体积v，最底层半径不能超过r，高度不能超过h
	//求出最小表面积放入minArea
	if (n == 0)
	{
		if (v)
		{
			return ERROR;
		}
		else
		{
			minArea = min(minArea, area);
			return OK;
		}
	}
	if (v <= 0)
	{
		return ERROR;
	}

	if (area > minArea || area + n*(n + 1)*(2 * n + 1) / 6 > minArea)//最优性剪枝
	{
		return ERROR;
	}
	if (h < n || r < n)//可行性剪枝a
	{
		return ERROR;
	}
	int sumV = 0;
	for (int i = r, j = h, k = 1; k <= n; k++, i--, j--)
	{
		sumV += i*i*j;
	}
	if (pow((n*(n + 1) / 2), 2) > v || sumV < v) //可行性剪枝b,c
	{
		return ERROR;
	}

	for (int rr = r; rr >= n; --rr) //为了达到n层蛋糕，则必须至少递减1，所以最底层半径至少n
	{
		if (n == M)//底面积
		{
			area = rr*rr;
		}
		if (area + 2 * v / rr> minArea)//放缩剪枝
		{
			return ERROR;
		}
		for (int hh = h; hh >= n; --hh) //同理，最底层高度至少n
		{
			area += 2 * rr*hh;

			Dfs(v - rr*rr*hh, n - 1, rr - 1,hh - 1);
			area -= 2 * rr*hh;
		}
	}
	return OK;
}
int main()
{
	cin >> N >> M;
	int maxR, maxH;
	//上面M-1层蛋糕的半径和高度一次递增1，即可求得最大半径和最大高度
	int residueV=0;
	int j = 1;//高度拟定值
	int i = 1;
	for (; i <= M - 1; i++)
	{
		residueV += i*i*(j++);
	}
	maxR =(int)sqrt(floor((N - residueV) / (double)j + 0.5));
	maxH = (int)floor((N - residueV) / (double)(i*i) + 0.5);
	Dfs(N, M, maxR, maxH);
	if (minArea == 1 << 30)
	{
		cout << 0 << endl;
	}
	else
	{
		cout << minArea << endl;
	}
	return 0;
}

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int OK = 1;
const int ERROR = 0;
typedef int Status;
int N, M;
int maxR, maxH;
int minArea = 1 << 30;
int Area;
int SubLevelV[21];
Status DFS(int v, int m, int r, int h)
{
	if (m == 0) //递归搭建蛋糕完毕
	{
		if (v == 0)
		{
			minArea = min(minArea, Area);
			return OK;
		}
		else
		{
			return ERROR;
		}
	}
	if (Area > minArea)
	{
		return ERROR;//最优性剪枝
	}
	if (SubLevelV[m] > v)
	{
		return ERROR;//当前剩余体积v不满足剩余层数m的搭建过程中所需的最小体积
	}

	for (int R = r; R >= m; R--)//每层最小半径和高度比为层数m，自证，不累述
	{
		for (int H = h; H >= m; H--)
		{
			if (m == M)
			{
				Area = R*R;//初始化投影底面积
			}
			if (minArea < Area + 2 * v / R)//放缩性剪枝
			{
				return ERROR;
			}
			int subV = v - R*R*H;
			if (subV >= 0)
			{
				Area += 2 * R*H;
				DFS(subV, m - 1, R - 1, H - 1);
				Area -= 2 * R*H;
			}
		}
	}
	return ERROR;
}
int main()
{
	cin >> N >> M;
	int r = 1;
	int h = 1;
	int ResidueV = 0;
	for (int k = 0; k < M - 1; k++)
	{
		ResidueV += r*r*h;
		SubLevelV[k + 1] = ResidueV;
		r++;
		h++;
	}
	maxR = (int)sqrt(ceil((N - ResidueV) / (double)h));//最大可行半径
	maxH = (int)ceil((N - ResidueV) / (double)(r*r));//最大可行高度
	DFS(N, M, maxR, maxH);
	if (minArea == 1 << 30)
	{
		cout << 0 << endl;
	}
	else
	{
		cout << minArea << endl;
	}
	return 0;
}

红与黑

描述
有一间长方形的房子，地上铺了红色、黑色两种颜色的正方形瓷砖。你站在其中一块黑色的瓷砖上，只能向相邻的黑色瓷砖移动。请写一个程序，计算你总共能够到达多少块黑色的瓷砖。
输入
包括多个数据集合。每个数据集合的第一行是两个整数W和H，分别表示x方向和y方向瓷砖的数量。W和H都不超过20。在接下来的H行中，每行包括W个字符。每个字符表示一块瓷砖的颜色，规则如下
1）‘.’：黑色的瓷砖；
2）‘#’：白色的瓷砖；
3）‘@’：黑色的瓷砖，并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。
当在一行中读入的是两个零时，表示输入结束。
输出
对每个数据集合，分别输出一行，显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。
样例输入

6 9
....#.
.....#
......
......
......
......
......
#@...#
.#..#.
0 0

样例输出
45
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：红与黑.cpp

解题思路：
深度优先搜索求连通面积

当前版本：1.0
作    者：Louris
完成日期：2017.09.06
*/

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define OK 1
#define ERROR 0
typedef int Status;
int W, H;
char arrays[21][21];
int visited[21][21];
int Area = 0;
Status Dfs(int i, int j)
{
	Area++;
	visited[i][j] = 1;
	if (i - 1 >= 1 && arrays[i - 1][j] == '.'&& visited[i - 1][j] != 1)
	{
		Dfs(i - 1, j);//向上走
	}
	if (i + 1 <= H&&arrays[i + 1][j] == '.'&& visited[i + 1][j] != 1)
	{
		Dfs(i + 1, j);//向下走
	}
	if (j - 1 >= 1 && arrays[i][j - 1] == '.'&& visited[i][j - 1] != 1)
	{
		Dfs(i, j - 1);//向左走
	}
	if (j + 1 <= W&&arrays[i][j + 1] == '.'&& visited[i][j + 1] != 1)
	{
		Dfs(i, j + 1);//向右走
	}
	return OK;
}
int main()
{

	while (cin >> W >> H&&W != 0 && H != 0)
	{
		int x, y;
		Area = 0;
		for (int i = 1; i <= H; i++)
		{
			for (int j = 1; j <= W; j++)
			{
				cin >> arrays[i][j];
				if (arrays[i][j] == '@')
				{
					x = i;
					y = j;
				}
			}
		}
		for (int i = 0; i < 21; i++)
		{
			fill(visited[i], visited[i] + 21, 0);
		}
		Dfs(x, y);
		cout << Area << endl;
	}
	return 0;
}

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：红与黑.cpp

解题思路：
深度优先搜索求连通面积
利用矩阵自身元素不同作为标志

当前版本：1.0
作    者：Louris
完成日期：2017.09.07
*/

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define OK 1
#define ERROR 0
typedef int Status;
int W, H;
char arrays[21][21];
int Area = 0;
Status Dfs(int i, int j)
{
	Area++;
	arrays[i][j] = '#';
	if (i - 1 >= 1 && arrays[i - 1][j] == '.')
	{
		Dfs(i - 1, j);//向上走
	}
	if (i + 1 <= H&&arrays[i + 1][j] == '.')
	{
		Dfs(i + 1, j);//向下走
	}
	if (j - 1 >= 1 && arrays[i][j - 1] == '.')
	{
		Dfs(i, j - 1);//向左走
	}
	if (j + 1 <= W&&arrays[i][j + 1] == '.')
	{
		Dfs(i, j + 1);//向右走
	}
	return OK;
}
int main()
{

	while (cin >> W >> H&&W != 0 && H != 0)
	{
		int x, y;
		Area = 0;
		for (int i = 1; i <= H; i++)
		{
			for (int j = 1; j <= W; j++)
			{
				cin >> arrays[i][j];
				if (arrays[i][j] == '@')
				{
					x = i;
					y = j;
				}
			}
		}
		Dfs(x, y);
		cout << Area << endl;
	}
	return 0;
}

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int OK = 1;
const int ERROR = 0;
typedef int Status;
const int MAXN = 20;
bool Visited[MAXN][MAXN];
int W, H;
char Map[MAXN][MAXN];
int Start_Row, Start_Col;
int nVisitCount = 0;
int Step[4][2]=
{
	 1, 0,
	-1, 0,
	 0,-1,
	 0, 1,
};//上下左右
Status DFS(int row, int col)
{
	nVisitCount++;
	Visited[row][col] = true;
	for (int i = 0; i < 4; i++)
	{
		int temp_row = row + Step[i][0];
		int temp_col = col + Step[i][1];
		if (temp_row >= 0 && temp_row < H&&temp_col >= 0 && temp_col < W
			&& !Visited[temp_row][temp_col] && Map[temp_row][temp_col] == '.')
		{
			DFS(temp_row, temp_col);
		}
	}
	return OK;
}
int main()
{
	while (cin >> W >> H && (W != 0 || H != 0))
	{
		nVisitCount = 0;
		memset(Visited, false, sizeof(Visited));
		for (int row = 0; row < H; row++)
		{
			for (int col = 0; col < W; col++)
			{
				cin >> Map[row][col];
				if (Map[row][col] == '@')
				{
					Start_Row = row;
					Start_Col = col;
				}
			}
		}
		DFS(Start_Row, Start_Col);
		cout << nVisitCount << endl;
	}
}

马走日

描述
马在中国象棋以日字形规则移动。
请编写一段程序，给定nm大小的棋盘，以及马的初始位置(x，y)，要求不能重复经过棋盘上的同一个点，计算马可以有多少途径遍历棋盘上的所有点。
*输入**
第一行为整数T(T < 10)，表示测试数据组数。
每一组测试数据包含一行，为四个整数，分别为棋盘的大小以及初始位置坐标n,m,x,y。(0<=x<=n-1,0<=y<=m-1, m < 10, n < 10)
输出
每组测试数据包含一行，为一个整数，表示马能遍历棋盘的途径总数，0为无法遍历一次。
样例输入
1
5 4 0 0
样例输出
32

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：马走日.cpp

解题思路：
典型深搜，和骑士那题一样

当前版本：1.0
作    者：Louris
完成日期：2017.09.23
*/
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define OK 1
#define ERROR 0
typedef int Status;
int Steps[8][2] =
{
	 1,-2,
	-1,-2,
	-2,-1,
	-2, 1,
	-1, 2,
	 1, 2,
	 2, 1,
	 2,-1,

};//每个点有八种可能的方向走
int visited[10][10];
int map[10][10];
int sum_paths;
int T, n, m, x, y;
int sum_points;
bool Judge(int row, int line)
{
	return row >= 0 && row < n&&line >= 0 && line < m;
}
Status DFS(int row, int line)
{
	sum_points++;
	visited[row][line] = 1;
	if (sum_points == n*m)
	{
		sum_paths++;
		//return OK
		//不能return，除非在这加上sum_points--和visited[row][line]=0
		//也就是说return后必须保证此点回溯
	}
	for (int i = 0; i < 8; i++)
	{
		int tempx = row + Steps[i][0];
		int tempy = line + Steps[i][1];
		if (Judge(tempx, tempy) && visited[tempx][tempy] == 0)
		{
			DFS(tempx, tempy);
		}
	}
	sum_points--;
	visited[row][line] = 0;
	return ERROR;
}
int main()
{
	cin >> T;
	while (T--)
	{
		cin >> n >> m >> x >> y;
		sum_points = sum_paths = 0;
		memset(visited, 0, sizeof(visited));
		DFS(x, y);
		cout << sum_paths << endl;
	}
	return 0;
}

A Knight’s Journey

描述
Background
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 × 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans?
　　　　　　　　　 A_Knight's_Journey图示
Problem
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.
输入
The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p × q <= 26. This represents a p × q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .
输出
The output for every scenario begins with a line containing “Scenario #i:”, where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number.
If no such path exist, you should output impossible on a single line.
样例输入
3
1 1
2 3
4 3
样例输出
Scenario #1:
A1

Scenario #2:
impossible

Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：A_Knight's_Journey.cpp

解题思路：
题目意思是说p * q的棋盘，马可以从任意位置出发，马的行走方式为长为3 宽为2的对角
求是否能够走完所有位置，如果可以则输出字母典序优先的路径
棋盘纵向数字编码，横向字母编码
字母典序优先，那么每一点的八种可能步骤可以按典序排练进行深搜。

有种生无可恋叫做，刚开始横纵坐标搞错，到最后发现典序顺序又搞错，打圈了都....emmmm......

当前版本：1.0
作    者：Louris
完成日期：2017.09.07
*/
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
#define OK 1
#define ERROR 0
typedef int Status;
int line, row;
int visited[26][26];
int Row[26];
char Line[26];
int Step[8][2] =
{
-2,-1,
-2, 1,
-1,-2,
-1, 2,
 1,-2,
 1, 2,
 2,-1,
 2, 1,
};
vector< pair<char, int> > location;
Status Dfs(int i, int j)
{
	//记录位置
	pair<char, int> temp;
	temp.first = Line[j];
	temp.second = Row[i];
	location.push_back(temp);
	//记录访问标记
	visited[i][j] = 1;
	//模拟可能的行走路径
	for (int k = 0; k < 8; k++)
	{
		int x = j + Step[k][0]; //横坐标
		int y = i + Step[k][1]; //纵坐标
		if (x >= 0 && x < line&&y >= 0 && y < row&&visited[y][x] != 1)
		{
			Dfs(y, x);
		}
	}
	if (location.size() != line*row)
	{
		visited[i][j] = 0;
		location.pop_back();
	}
	return ERROR;
}
int main()
{
	int n;
	for (int i = 0; i < 26; i++)
	{
		Row[i] = i + 1;
		Line[i] = 'A' + i;
	}
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> row >> line;
		location.clear();
		memset(visited, 0, sizeof(visited));
		Dfs(0, 0);
		cout << "Scenario #" << i << ":" << endl;
		if (location.size() == 0)
		{
			cout << "impossible" << endl;
		}
		else
		{
			for (vector< pair<char, int> >::iterator it = location.begin(); it != location.end(); it++)
			{
				cout << it->first << it->second;
			}
			cout << endl;
		}
		if (i != n)
		{
			cout << endl;
		}
	}
	return 0;
}

#include<iostream>
#include<algorithm>
#include<cstring>
#include<deque>
using namespace std;
const int OK = 1;
const int ERROR = 0;
typedef int Status;
const int MAXN = 26;
int Row[MAXN];
char Col[MAXN];
bool Visited[MAXN][MAXN];
deque< pair<char, int> >dq;
int Step[8][2]=
{
	-1,-2,
	 1,-2,
	-2,-1,
	 2,-1,
	-2, 1,
	 2, 1,
	-1, 2,
	 1, 2,
};
int p, q;
Status DFS(int row, int col)
{
	pair<char, int> temp;
	temp.first = Col[col];
	temp.second = Row[row];
	dq.push_back(temp);
	Visited[row][col] = true;

	for (int i = 0; i < 8; i++)
	{
		int temp_row = row + Step[i][0];
		int temp_col = col + Step[i][1];
		if (!Visited[temp_row][temp_col] && temp_row < p&&temp_col >= 0 && temp_row >= 0 && temp_col < q)
		{
			DFS(temp_row, temp_col);
		}
	}
	if (dq.size() != p*q)
	{
		dq.pop_back();
		Visited[row][col] = false;
	}
	return OK;
}

int main()
{
	for (int i = 0; i < MAXN; i++)
	{
		Row[i] = i + 1;
		Col[i] = 'A' + i;
	}
	int nCase;
	cin >> nCase;
	for (int i = 1; i <= nCase; i++)
	{
		cin >> p >> q;
		memset(Visited, false, sizeof(Visited));
		DFS(0, 0);
		cout << "Scenario #" << i << ":" << endl;
		if (dq.empty())
		{
			cout << "impossible" << endl;
		}
		else
		{
			while (!dq.empty())
			{
				pair<char, int> temp = dq.front();
				cout << temp.first << temp.second;
				dq.pop_front();
			}
			cout << endl;
		}
		if (i != nCase)
		{
			cout << endl;
		}
	}
	return 0;
}

Sudoku

描述
Sudoku is a very simple task. A square table with 9 rows and 9 columns is divided to 9 smaller squares 3x3 as shown on the Figure. In some of the cells are written decimal digits from 1 to 9. The other cells are empty. The goal is to fill the empty cells with decimal digits from 1 to 9, one digit per cell, in such way that in each row, in each column and in each marked 3x3 subsquare, all the digits from 1 to 9 to appear. Write a program to solve a given Sudoku-task.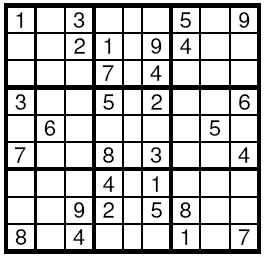
Suduku图示
输入
The input data will start with the number of the test cases. For each test case, 9 lines follow, corresponding to the rows of the table. On each line a string of exactly 9 decimal digits is given, corresponding to the cells in this line. If a cell is empty it is represented by 0.
输出
For each test case your program should print the solution in the same format as the input data. The empty cells have to be filled according to the rules. If solutions is not unique, then the program may print any one of them.
样例输入
1
103000509
002109400
000704000
300502006
060000050
700803004
000401000
009205800
804000107
样例输出
143628579
572139468
986754231
391542786
468917352
725863914
237481695
619275843
854396127
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：Sudoku.cpp

解题思路：
深搜：
将每一行、每一列、每一个小九宫格用三个数组判重
同时只记录未填入数字的格子数进行深搜，加快深搜速度

当前版本：1.0
作    者：Louris
完成日期：2017.09.23
*/
#include<iostream>
#include<cstring>
using namespace std;
#define OK 1
#define ERROR 0
typedef int Status;
int map[10][10];
int Count;
bool row[10][10];
bool column[10][10];
bool subsquare[10][10];
struct Node
{
	int x;
	int y;
	Node(int xx, int yy) :x(xx), y(yy) {}
	Node() {}
}Points[100];
int Judge(int i, int j) //规定每个小九宫格的号码
{
	return ((i - 1) / 3 )* 3 + (j - 1) / 3 + 1;
	/*
	 1 2 3
	 4 5 6
	 7 8 9

	 1+3*0 2+3*0 3+3*0
	 1+3*1 2+3*1 3+3*1
	 1+3*2 2+3*2 3+3*2
	*/
}
Status DFS(int n)
{
	if (n > Count)
	{
		return OK;
	}
	//每个空点都有1-9九种可能
	for (int i = 1; i <= 9; i++)
	{
		if (!row[Points[n].x][i] && !column[i][Points[n].y] && !subsquare[Judge(Points[n].x, Points[n].y)][i])
		{
			row[Points[n].x][i] = true;
			column[i][Points[n].y] = true;
			subsquare[Judge(Points[n].x, Points[n].y)][i] = true;
			map[Points[n].x][Points[n].y] = i;
			if (DFS(n + 1))
			{
				return OK;
			}
			row[Points[n].x][i] = false;
			column[i][Points[n].y] = false;
			subsquare[Judge(Points[n].x, Points[n].y)][i] = false;
		}
	}
	return ERROR;
}
int main()
{
	int t;
	cin >> t;
	while (t--)
	{
		Count = 0;
		memset(row, false, sizeof(row));
		memset(column, false, sizeof(column));
		memset(subsquare, false, sizeof(subsquare));
		memset(map, 0, sizeof(map));
		for (int i = 1; i <= 9; i++)
		{
			for (int j = 1; j <= 9; j++)
			{
				scanf("%1d", &map[i][j]);
				if (map[i][j] != 0)
				{
					row[i][map[i][j]] = true;
					column[map[i][j]][j] = true;
					subsquare[Judge(i, j)][map[i][j]] = true;
				}
				else
				{
					Count++;
					Points[Count].x = i;
					Points[Count].y = j;
				}
			}
		}
		DFS(1);//从第一个空点深搜
		for (int i = 1; i <= 9; i++)
		{
			for (int j = 1; j <= 9; j++)
			{
				cout << map[i][j];
			}
			cout << endl;
		}
	}
	return 0;
}

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int OK=1;
const int ERROR=0;
typedef int Status;
struct CNode
{
	int row;
	int col;
}ZeroPoint[100];
int Map[10][10];
bool SubRow[10][10];
bool SubCol[10][10];
bool SubSquare[10][10];
int nNodeCount;//0节点个数
int Locate(int row,int col)
{
	return (row/3)*3+col/3;
}
bool Judge(int row,int col,int val)
{
	if(SubRow[row][val]||SubCol[val][col]||SubSquare[Locate(row,col)][val])
	{
		return false;
	}
	return true;
}
Status DFS(int n)
{
	if(n==nNodeCount)
	{
		return OK;
	}
	for(int i=1;i<=9;i++)
	{
		if(Judge(ZeroPoint[n].row,ZeroPoint[n].col,i))
		{
			SubRow[ZeroPoint[n].row][i]=true;
			SubCol[i][ZeroPoint[n].col]=true;
			SubSquare[Locate(ZeroPoint[n].row,ZeroPoint[n].col)][i]=true;
			Map[ZeroPoint[n].row][ZeroPoint[n].col]=i;
			if(DFS(n+1))
			{//截断，如果得到一个正确结果就终止递归！
				return OK;
			}
			Map[ZeroPoint[n].row][ZeroPoint[n].col]=0;
			SubRow[ZeroPoint[n].row][i]=false;
			SubCol[i][ZeroPoint[n].col]=false;
			SubSquare[Locate(ZeroPoint[n].row,ZeroPoint[n].col)][i]=false;
		}
	}
	return ERROR;
}
int main()
{
	int nCase;
	int temp;
	cin>>nCase;
	while(nCase--)
	{
		nNodeCount=0;
		memset(Map,0,sizeof(Map));
		memset(SubRow,false,sizeof(SubRow));
		memset(SubCol,false,sizeof(SubCol));
		memset(SubSquare,false,sizeof(SubSquare));
		for(int row=0;row<9;row++)
		{
			for(int col=0;col<9;col++)
			{

				scanf("%1d",&temp);
				if(temp!=0)
				{
					Map[row][col]=temp;
					SubRow[row][temp]=true;
					SubCol[temp][col]=true;
					SubSquare[Locate(row,col)][temp]=true;
				}
				else
				{
					ZeroPoint[nNodeCount].row=row;
					ZeroPoint[nNodeCount].col=col;
					nNodeCount++;
				}
			}
		}
		DFS(0);
		for(int row=0;row<9;row++)
		{
			for(int col=0;col<9;col++)
			{
				cout<<Map[row][col];
			}
			cout<<endl;
		}
	}
	return 0;
}

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int OK = 1;
const int ERROR = 0;
typedef int Status;
const int MAXN = 10;
struct CNode
{
	int row;
	int col;
}ZeroPoint[MAXN*MAXN];
bool bRow[MAXN][MAXN];
bool bCol[MAXN][MAXN];
bool bSubsquare[MAXN][MAXN];
int nZeroCount = 0;
int Map[MAXN][MAXN];
int tempCount = 0;
int LocateSubsquare(int row, int col)
{
	return (row / 3) * 3 + col / 3;
}
Status DFS(int n)
{
	tempCount++;
	for (int i = 1; i <= 9; i++)
	{
		int row = ZeroPoint[n].row;
		int col = ZeroPoint[n].col;
		if (!bRow[row][i] && !bCol[i][col] && !bSubsquare[LocateSubsquare(row, col)][i])
		{
			Map[row][col] = i;
			bRow[row][i] = true;
			bCol[i][col] = true;
			bSubsquare[LocateSubsquare(row, col)][i] = true;
			DFS(n + 1);
			if (tempCount == nZeroCount+1)
			{
				return OK;
			}
			tempCount--;
			Map[row][col] = 0;
			bRow[row][i] = false;
			bCol[i][col] = false;
			bSubsquare[LocateSubsquare(row, col)][i] = false;
		}
	}
	return ERROR;
}
int main()
{
	int nCase;
	cin >> nCase;
	while (nCase--)
	{
		nZeroCount = tempCount = 0;
		memset(bRow, false, sizeof(bRow));
		memset(bCol, false, sizeof(bCol));
		memset(bSubsquare, false, sizeof(bSubsquare));
		memset(Map, 0, sizeof(Map));
		for (int row = 0; row < MAXN - 1; row++)
		{
			for (int col = 0; col < MAXN - 1; col++)
			{
				scanf("%1d", &Map[row][col]);
				if (Map[row][col] != 0)
				{
					bRow[row][Map[row][col]] = true;
					bCol[Map[row][col]][col] = true;
					bSubsquare[LocateSubsquare(row, col)][Map[row][col]] = true;
				}
				else
				{
					ZeroPoint[nZeroCount].row = row;
					ZeroPoint[nZeroCount].col = col;
					nZeroCount++;
				}
			}
		}
		DFS(0);
		for (int row = 0; row < MAXN - 1; row++)
		{
			for (int col = 0; col < MAXN - 1; col++)
			{
				cout << Map[row][col];
			}
			cout << endl;
		}
	}
	return 0;
}

棋盘问题

描述
在一个给定形状的棋盘（形状可能是不规则的）上面摆放棋子，棋子没有区别。要求摆放时任意的两个棋子不能放在棋盘中的同一行或者同一列，请编程求解对于给定形状和大小的棋盘，摆放k个棋子的所有可行的摆放方案C。
输入
输入含有多组测试数据。
每组数据的第一行是两个正整数，n,k，用一个空格隔开，表示了将在一个n×n的矩阵内描述棋盘，以及摆放棋子的数目。
n <= 8 , k <= n
当为-1 -1时表示输入结束。
随后的n行描述了棋盘的形状：每行有n个字符，其中 # 表示棋盘区域，.表示空白区域（数据保证不出现多余的空白行或者空白列）。
输出
对于每一组数据，给出一行输出，输出摆放的方案数目C （数据保证C<2^31）。
样例输入

2 1
#.
.#
4 4
...#
..#.
.#..
#...
-1 -1

样例输出
2
1
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：棋盘问题.cpp

解题思路：
与N皇后问题相同，只不过是棋盘形状的不规则，并且棋子个数随输入而定
深搜:
每个位置都可放可不放，进行所有可能性，有点像动规
每一行可能的位置进行枚举，但要注意可以整行都没有棋子，每行棋子最多一个
在对当行所有可能位置进行枚举放置的同时，与之前行棋子位置进行判断，确保不再同列

剪枝：
①剩余行数小于需要摆放的棋子个数
②行数没满，棋子个数为0

AC时间：
未剪枝：53ms
剪枝：7ms

思路还行，有N皇后的经验借鉴，然而小毛病还是有啊x打错成k，天了噜

当前版本：1.0
作    者：Louris
完成日期：2017.09.08
*/
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define OK 1
#define ERROR 0
typedef int Status;
int n, k;
char Chessboard[8][8];
int Chesslocation[8];//记录每行棋子位置
int sum;
Status Dfs(int row, int x)
{
	if (row == n)
	{
		if (x == 0)
		{
			sum++;
			return OK;
		}
		else
		{
			return ERROR;
		}
	}
	if (row != n&&x == 0)//剪枝
	{
		sum++;
		return OK;
	}
	if (n - row < x) //剪枝
	{
		return ERROR;
	}
	for (int i = 0; i < n; i++) //列枚举
	{
		if (Chessboard[row][i] == '#')
		{
			int j;
			for (j = 0; j < row; j++) //与之前的行进行比较
			{
				if (Chesslocation[j] == i)
				{
					break;
				}
			}
			if (j == row)
			{
				Chesslocation[row] = i;//放
				Dfs(row + 1, x - 1);
				Chesslocation[row] = -1;//不放
			}
		}
		if (i == n - 1)
		{
			Dfs(row + 1, x);//空行
		}
	}
	return OK;
}
int main()
{
	while (cin >> n >> k&&n != -1 && k != -1)
	{
		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < n; j++)
			{
				cin >> Chessboard[i][j];
			}
		}
		sum = 0;
		memset(Chesslocation, -1, sizeof(Chesslocation));
		Dfs(0, k);
		cout << sum << endl;
	}
	return 0;
}

第六章广度优先搜索

广搜与深搜的比较

1.广搜一般用于状态表示比较简单、求最优策略的问题
优点：是一种完备策略，即只要问题有解，它一定可以找到解，并且，广度优先搜索找到的解，还一定是路径最短的解。
缺点：盲目性较大，尤其是当目标节点距初始节点较远时，将产生许多无用的节点，因此其搜索效率较低。需要保存所有扩展出的状态，占用的空间大
2.深搜几乎可以用于任何问题
只需要保存从起始状态到当前状态路径上的节点
广度优先搜索算法如下：
a.把初始结点S0放入Open表中；
b.如果Open表为空，则问题无解，失败退出；
c.把Open表的第一个节点取出放入Closed表，并记该节点为n；
d.考察节点n是否为目标节点。若是，则得到问题的解，成功退出；
e.若结点n不可扩展，则转b；
f.扩展节点n，将其不再Closed表和Open表中的子节点（判重）放入Open表的尾部，并为每一个子节点设置指向父节点的指针（或记录节点的层次），然后转b。

抓住那头牛

描述
农夫知道一头牛的位置，想要抓住它。农夫和牛都位于数轴上，农夫起始位于点 N(0<=N<=100000)，牛位于点 K(0<=K<=100000)。农夫有两种移动方式：
1、从X移动到X-1或X+1，每次移动花费一分钟
2、从X移动到2×X，每次移动花费一分钟
假设牛没有意识到农夫的行动，站在原地不动。农夫最少要花多少时间才能抓住牛？
输入
两个整数，N和K
输出
一个整数，农夫抓到牛所要花费的最小分钟数
样例输入
5 17
样例输出
4
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：抓住那头牛.cpp

解题思路：
假设农夫起始位置位于点3，牛位于点5，N=3，K=5，最右边是6
如何搜索一条走到5的路径
0<->1
1<->2
2->4
2<->3
3->6
3<->4
4<->5
5->6

1.深度优先搜索：
从起点出发，随机调一个方向，能往前走就往前走（扩展），走不动了则回溯。
不能走已经走过的点（要判重）。
运气不太好：
3->2->4->5
运气最坏的话：
3->2->1->0->4->5
要想求最优解，则要遍历所有走法。可以用各种手段优化，比如，若已经找到路径长度为n的解
则所有长度大于n的走法就不比尝试。
运算过程中需要存储路径上的结点，数量较少。

2.广度优先搜索：
给节点分层。起点是第0层，从起点最少需n步就能到达的点属于第n层。

依层次顺序，从小到大扩展节点。把层次低的点全部扩展出来后，才会扩展层次高的点。

搜索过程（节点扩展过程）：
3
2 4 6
1 5
0

可确保找到最优解，但是因扩展出来的节点较多，且多数节点都需要保存，
因此需要的存储空间较大，用队列存节点。

当前版本：1.0
作    者：Louris
完成日期：2017.09.09
*/
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
int N, K;
const int MAXN = 100000;
int visited[MAXN + 10]; //判重标记
struct Step
{
	int x;
	int steps;
	Step(int xx, int s) :x(xx), steps(s)
	{

	}
};
queue<Step> q;
int main()
{
	cin >> N >> K;
	memset(visited, 0, sizeof(visited));
	q.push(Step(N, 0));
	visited[N] = 1;
	while (!q.empty())
	{
		Step s = q.front();
		if (s.x == K)
		{
			cout << s.steps << endl;
			return 0;
		}
		else
		{
			if (s.x - 1 >= 0 && !visited[s.x - 1])
			{
				q.push(Step(s.x - 1, s.steps + 1));
				visited[s.x - 1] = 1;
			}
			if (s.x + 1 <=MAXN && !visited[s.x + 1])
			{
				q.push(Step(s.x + 1, s.steps + 1));
				visited[s.x + 1] = 1;
			}
			if (s.x * 2 <= MAXN && !visited[s.x * 2])
			{
				q.push(Step(s.x * 2, s.steps + 1));
				visited[s.x * 2] = 1;
			}
      q.pop();
		}

	}
  return 0;
}

迷宫问题

描述
定义一个二维数组，它表示一个迷宫，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。
输入
一个5 × 5的二维数组，表示一个迷宫。数据保证有唯一解。
输出
左上角到右下角的最短路径，格式如样例所示。
样例输入
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
样例输出
(0, 0)
(1, 0)
(2, 0)
(2, 1)
(2, 2)
(2, 3)
(2, 4)
(3, 4)
(4, 4)
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：迷宫问题.cpp

解题思路：
基础广搜。
先将起始位置入队列，每次从队列拿出一个元素，扩展其相邻的4个元素入队列（要判重）
直到队头元素为终点为止。队列里的元素记录了指向父节点（上一步）的指针。

队列元素：
struct
{
  int r,c; //位置
  int f; //父节点在队列中的下标
}

队列不能用STL的queue或deque，要自己写。
用一维数组实现，维护一个队头指针和队尾指针。

有一种生无可恋叫做，while循环里面不更替！我他妈神经病！

当前版本：1.0
作    者：Louris
完成日期：2017.09.09
*/
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
struct Node
{
	int x;
	int y;
	int father;
	Node(int dx, int dy, int df) :x(dx), y(dy), father(df){}
};
int map[5][5]; //自身也为标志数组
vector<Node> v;
int num = 0;
queue<Node> q;
int Step[4][2] =
{
	 1, 0,
	-1, 0,
	 0, 1,
	 0,-1,
};
int main()
{
	for (int i = 0; i < 5; i++)
	{
		for (int j = 0; j < 5; j++)
		{
			cin >> map[i][j];
		}
	}
	//广搜
	q.push(Node(0, 0, -1)); //起点入队列
	v.push_back(Node(0, 0, -1));
	map[0][0] = 1;
	while (!q.empty())
	{
		Node s = q.front();
		if (s.x == 4 && s.y == 4)
		{
			vector<Node> temp;
			temp.push_back(s);//终点
			while (s.father != -1)
			{
				temp.push_back(v[s.father]);
				s = v[s.father];
			}
			for (vector<Node>::reverse_iterator rit = temp.rbegin(); rit != temp.rend(); rit++)
			{
				cout << "(" << rit->x << ", " << rit->y << ")" << endl;
			}
			return 0;
		}
		else
		{
			for (int i = 0; i < 4; i++)
			{
				int x = s.x + Step[i][0]; //纵坐标
				int y = s.y + Step[i][1]; //横坐标
				if (x >= 0 && x < 5 && y >= 0 && y < 5)
				{
					if (map[x][y] != 1)
					{
						q.push(Node(x, y, num));
						v.push_back(Node(x, y, num));
						map[x][y] = 1;
					}
				}
			}
			num++;
			q.pop();
		}

	}
	return 0;
}

鸣人和佐助

描述
佐助被大蛇丸诱骗走了，鸣人在多少时间内能追上他呢？
已知一张地图（以二维矩阵的形式表示）以及佐助和鸣人的位置。地图上的每个位置都可以走到，只不过有些位置上有大蛇丸的手下，需要先打败大蛇丸的手下才能到这些位置。鸣人有一定数量的查克拉，每一个单位的查克拉可以打败一个大蛇丸的手下。假设鸣人可以往上下左右四个方向移动，每移动一个距离需要花费1个单位时间，打败大蛇丸的手下不需要时间。如果鸣人查克拉消耗完了，则只可以走到没有大蛇丸手下的位置，不可以再移动到有大蛇丸手下的位置。佐助在此期间不移动，大蛇丸的手下也不移动。请问，鸣人要追上佐助最少需要花费多少时间？
输入
输入的第一行包含三个整数：M，N，T。代表M行N列的地图和鸣人初始的查克拉数量T。0 < M,N < 200，0 ≤ T < 10
后面是M行N列的地图，其中@代表鸣人，+代表佐助。*代表通路，#代表大蛇丸的手下。
输出
输出包含一个整数R，代表鸣人追上佐助最少需要花费的时间。如果鸣人无法追上佐助，则输出-1。
样例输入

4 4 1
#@##
**##
###+
****

4 4 2
#@##
**##
###+
****

样例输出
6
4
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：鸣人和佐助.cpp

解题思路：
深搜：
四个方向枚举，同时判断引入查克拉数量，判断是否可走。
走过的地标记为起点字符@，因为最短时间的路径不可能走回起点

剪枝：
①可行性剪枝：
当发现当前时间已经比最优时间长却还没有到达时，可以剪枝

②最优性剪枝：
有没有这种可能：
时间不是最小，查克拉数量比较多能够到达，
而其他情况时间最小但是查克拉数量较少到达不了？有！！！
t=1
*@***
*####
*#***
***##
####+
所以不能剪枝
时间更小，查克拉数量也比较小能够达到吗？有！！！
t=1
*@***
*####
*#***
***#*
####+
所以不能剪枝
a.查克拉数量少于当前记录值，可以剪枝

③预测性剪枝：
比较鸣人和佐助的位置，如果当前搜索到的位置加上距离佐助位置最少步数后
大于当前最优解，那么可以剪枝。

三维数组补漏洞：
之前只记录了时间小，查克拉数量多的情况，而实际上面说的时间更小，查克拉也更小的情况没有被记录
所以开三维数组进行记录，剔除当前查克拉数量的前提下的位置的时间更大的情况。

简化分析：
还是把查克拉当成定量分析吧....
我去掉record 直接剩下mark更快..

record下的time和td都是变量，比较起来麻烦而且有漏洞，
mark下的记录把查克拉定量化了，相当于只有一个时间的变量，思路更清晰

就前面两个分析的来说，
时间不是最小，查克拉多可以过
时间小，查克拉也少也可以过
所以都得记录，三维数组可能是最好的选择了

当前版本：1.0
作    者：Louris
完成日期：2017.09.08
*/
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
#define OK 1
#define ERROR 0
typedef int Status;
#define inf 0x3f3f3f3f
int M, N, T;
char map[200][200];
int minTime;
int Time;
int zx, zy;//佐助的坐标
int Step[4][2] =
{
	-1, 0,
	 1, 0,
	 0,-1,
	 0, 1,
};
/*struct Record
{
	int time;
	int td;
}record[200][200];*/
int mark[200][200][10];
Status Dfs(int i, int j, int t)
{
	Time++;
	map[i][j] = '@'; //走过
	if (Time >= minTime) //剪枝
	{
		return ERROR;
	}
	if (Time >= mark[i][j][t]) //补漏洞，剔除当前查克拉数量的前提下的位置的时间更大的情况
	{
		return ERROR;
	}
	mark[i][j][t] = Time;
	/*if (Time <= record[i][j].time)
	{
		if (t >= record[i][j].td)
		{
			record[i][j].time = Time;
			record[i][j].td = t;
		}
	}

	if (t < record[i][j].td)//剪枝，无论当前时间与记录的时间大小如何，只要查克拉数量小就可以剪枝
	{
		return ERROR;
	}

	if (record[i][j].time != 1 << 30 && record[i][j].time + fabs(zx - i) + fabs(zy - j) > minTime)//预测性剪枝
	{
		return ERROR;
	}
	if (Time + fabs(zx - i) + fabs(zy - j) > minTime)//预测性剪枝
	{
		return ERROR;
	}*/
	for (int k = 0; k < 4; k++) //上下左右四步枚举
	{
		int x = j + Step[k][1]; //横坐标
		int y = i + Step[k][0]; //纵坐标
		if (x >= 0 && x < N&&y >= 0 && y < M)
		{
			if (map[y][x] == '+')
			{
				Time++;
				minTime = min(Time, minTime);
				Time--;
				return OK;
			}
			if (map[y][x] == '#'&&t > 0)
			{
				Dfs(y, x, t - 1);
				map[y][x] = '#';
				Time--;
			}
			if (map[y][x] == '*')
			{
				Dfs(y, x, t);
				map[y][x] = '*';
				Time--;
			}
		}
	}
	return ERROR;
}
int main()
{
	while (cin >> M >> N >> T)
	{
		/*for (int i = 0; i < M; i++)
		{
			for (int j = 0; j < N; j++)
			{
				record[i][j].time = 1 << 30;
				record[i][j].td = 0;
			}
		}*/
		memset(mark, inf, sizeof(mark));
		int x, y;
		for (int i = 0; i < M; i++)
		{
			for (int j = 0; j < N; j++)
			{
				cin >> map[i][j];
				if (map[i][j] == '@')
				{
					x = i;
					y = j;
				}
				if (map[i][j] == '+')
				{
					zx = i;
					zy = j;
				}
			}
		}
		minTime = 1 << 30;
		Time = -1;
		Dfs(x, y, T);
		if (minTime == 1 << 30)
		{
			cout << -1 << endl;
		}
		else
		{
			cout << minTime << endl;
		}
	}
	return 0;
}

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：鸣人和佐助_广搜版.cpp

解题思路：
广搜：
形如迷宫问题
状态定义为：
(r,c,k)，鸣人所在的行，列和查克拉数量

如果队头节点扩展出来的节点是有大蛇手下的节点，则其k值比队头的k要减掉1。
如果队头节点的查克拉数量为0，则不能扩展出有大蛇手下的节点。

刚开始想得太简单了
广搜进行时，不代表已经走过的点就不能走，有可能当前到达的点从不同点走过来，
查克拉不一样，应当记录那个查克拉最大的一个走法

这是与迷宫问题最大的区别。

经分析，不存在同层元素相互连通的情况，最多只有子元素的父元素有两个的情况，
那么都加进队列，因为最终能到达的话路径一样长，无所谓查克拉大小了。

在当层元素扩展完子元素后标记使其不得返回上层。

当前版本：1.0
作    者：Louris
完成日期：2017.09.09
*/
#include<iostream>
#include<algorithm>
#include<cstring>
#include<deque>
using namespace std;
int M, N, T;
char map[200][200];
int maxT[200][200];
struct Node
{
	int x;
	int y;
	int t;
	int time;
	Node(int xx, int yy, int tt, int times) :x(xx), y(yy), t(tt), time(times) {}
};
deque<Node> q;
int Step[4][2] =
{
  1, 0,
 -1, 0,
  0, 1,
  0,-1,
};
int main()
{
	while (cin >> M >> N >> T)
	{
		int x, y;
		int a, b;
		for (int i = 0; i < M; i++)
		{
			for (int j = 0; j < N; j++)
			{
				cin >> map[i][j];
				if (map[i][j] == '@')
				{
					x = i;
					y = j;
				}
				if (map[i][j] == '+')
				{
					a = i;
					b = j;
				}
			}
		}
		memset(maxT, -1, sizeof(maxT));
		//广搜
		q.push_back(Node(x, y, T, 0));
		while (!q.empty())
		{
			Node s = q.front();
			if (s.x == a&&s.y == b)
			{
				cout << s.time << endl;
				break;
			}
			else
			{
				for (int i = 0; i < 4; i++)
				{
					int m = s.x + Step[i][0];
					int n = s.y + Step[i][1];
					if (m >= 0 && m < M&&n >= 0 && n < N&&maxT[m][n] < s.t)
					{
						Node temp(m, n, s.t, s.time + 1);
						if (map[m][n] == '@')
						{
							continue;
						}
						if (map[m][n] == '#')
						{
							temp.t = s.t - 1;
						}
						if (temp.t < 0)
						{
							continue;
						}
						maxT[m][n] = temp.t;
						q.push_back(temp);
					}
					//精简前冗杂代码段
					/*if (m >= 0 && m < M&&n >= 0 && n < N)
					{
						if (map[m][n] == '#')
						{
							if (s.t > 0)
							{
								if (maxT[m][n] < s.t - 1)
								{
									maxT[m][n] = s.t - 1;
									q.push_back(Node(m, n, s.t - 1, s.time + 1));
								}
							}
						}
						else if (map[m][n] != '@')
						{
							if (maxT[m][n] < s.t)
							{
								maxT[m][n] = s.t;
								q.push_back(Node(m, n, s.t, s.time + 1));
							}
						}
					}*/
				}
				map[s.x][s.y] = '@';//不能往回走，必须逐层向下
			}
			q.pop_front();
		}
		if (q.empty())
		{
			cout << -1 << endl;
		}
		q.clear();//清空
	}
	return 0;
}

单词序列

描述
给出两个单词（开始单词和结束单词）以及一个词典。找出从开始单词转换到结束单词，所需要的最短转换序列。转换的规则如下：
1、每次只能改变一个字母
2、转换过程中出现的单词(除开始单词和结束单词)必须存在于词典中
例如：
开始单词为：hit
结束单词为：cog
词典为：[hot,dot,dog,lot,log,mot]
那么一种可能的最短变换是： hit -> hot -> dot -> dog -> cog,
所以返回的结果是序列的长度5；
注意：
1、如果不能找到这种变换，则输出0；
2、词典中所有单词长度一样；
3、所有的单词都由小写字母构成；
4、开始单词和结束单词可以不在词典中。
输入
共两行，第一行为开始单词和结束单词（两个单词不同），以空格分开。第二行为若干的单词（各不相同），以空格分隔开来，表示词典。单词长度不超过5,单词个数不超过30。
输出
输出转换序列的长度。
样例输入
hit cog
hot dot dog lot log
样例输出
5
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：单词序列.cpp

解题思路：
基础广搜！
关键字：最短转换！

当前版本：1.0
作    者：Louris
完成日期：2017.09.23
*/
#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<deque>
using namespace std;
#define OK 1
#define ERROR 0
typedef int Status;
string str[32];
string Begin, End;
struct Node
{
	string s;
	int step;
	Node(string ss, int st) :s(ss), step(st) {}
	Node() {}
};
deque<Node> q;
int visited[32];
int main()
{
	while (cin >> Begin >> End)
	{
		//Begin = "hit";
		//End = "cog";
		str[0] = Begin; //加入后方便判重
		int num = 1;
		while (cin >> str[num])
		{
			num++;
		}
		/*str[1] = "hot";
		str[2] = "dot";
		str[3] = "dog";
		str[4] = "lot";
		str[5] = "log";
		num = 6;*/
		str[num] = End; //加入后方便判重
		//BFS
		memset(visited, 0, sizeof(visited));
		q.push_back(Node(str[0], 1));
		visited[0] = 1;
		while (!q.empty())
		{
			Node temp= q.front();

			if (temp.s == str[num])
			{
				cout << temp.step << endl;
				break;
			}
			for (int i = 1; i <= num; i++)
			{
				int tempn = 0;
				for (unsigned int j = 0; j < Begin.size(); j++)
				{
					if (temp.s[j] != str[i][j])
					{
						tempn++;
					}
				}
				if (tempn == 1&&visited[i]==0)
				{
					q.push_back(Node(str[i], temp.step + 1));
					visited[i] = 1;
				}
			}
			q.pop_front();
		}
		if (q.empty())
		{
			cout << 0 << endl;
		}
		q.clear();
	}
	return 0;
}

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<string>
#include<queue>
using namespace std;
const int OK=1;
const int ERROR=0;
typedef int Status;
struct CNode
{
	string str;//单词
	int step;
	CNode(string ss,int ff):str(ss),step(ff){};
	CNode(){};
};
vector<CNode> v;
deque<CNode>dq;
string Start,End;
vector<string> Dictionary;

bool Judge(string a,string b)
{
	int num=0;
	for(unsigned int i=0;i<a.length();i++)
	{
		if(a[i]!=b[i])
		{
			num++;
		}
	}
	if(num==1)
	{
		return true;
	}
	return false;
}
int main()
{
	while(cin>>Start>>End)
	{
		string ss;
		Dictionary.push_back(Start);//起点入字典，方便判重
		while(cin>>ss)
		{
			Dictionary.push_back(ss);
		}
		Dictionary.push_back(End);//终点入字典，方便判重
		bool *Visited = new bool[Dictionary.size()];
		fill(Visited, Visited + Dictionary.size(), false);
		dq.push_back(CNode(Start,1));//起点入队列
		v.push_back(CNode(Start,1));
		Visited[0]=true;

		while(!dq.empty())
		{
			CNode temp=dq.front();
			if(temp.str==End)
			{
				cout << temp.step << endl;
				break;
			}
			for(unsigned int i=0;i<Dictionary.size();i++)
			{
				if(Judge(temp.str,Dictionary[i])&&!Visited[i])
				{
					dq.push_back(CNode(Dictionary[i],temp.step+1));
					v.push_back(CNode(Dictionary[i],temp.step+1));
					Visited[i]=true;
				}
			}
			dq.pop_front();
		}
		if(dq.empty())
		{
			cout<<0<<endl;
		}
		dq.clear();
		v.clear();
		delete[] Visited;
	}
	return 0;
}

Pots

描述
You are given two pots, having the volume of A and B liters respectively. The following operations can be performed:
FILL(i): fill the pot i (1 ≤ i ≤ 2) from the tap;
DROP(i): empty the pot i to the drain;
POUR(i,j): pour from pot i to pot j; after this operation either the pot j is full (and there may be some water left in the pot i), or the pot i is empty (and all its contents have been moved to the pot j).
Write a program to find the shortest possible sequence of these operations that will yield exactly C liters of water in one of the pots.
输入
On the first and only line are the numbers A, B, and C. These are all integers in the range from 1 to 100 and C≤max(A,B).
输出
The first line of the output must contain the length of the sequence of operations K. The following K lines must each describe one operation. If there are several sequences of minimal length, output any one of them. If the desired result can’t be achieved, the first and only line of the file must contain the word ‘impossible’.
样例输入
3 5 4
样例输出
6
FILL(2)
POUR(2,1)
DROP(1)
POUR(2,1)
FILL(2)
POUR(2,1)
程序

/*
Copyright(c)2017, Louris
All rights reserved.

文件名称：Pots.cpp

解题思路：
题目的意思是给两个桶，给出三种操作：
a.填满
b.清空
c.转移
每组数据给出两个桶的容量和最终需要的水的体积，问最少步骤如何进行，并输出。

状态：
设(i,j)为瓶1与瓶2在某一时刻的容量，那么从这点出发，可以到达的点有：
①(A,j): FILL(1)
②(i,B): FILL(2)
③(0,j): DROP(1)
④(i,0): DROP(2)
⑤(i+j,0) or (A,j-A+i): POUR(2,1)
⑥(0,i+j) or (i-B+j,B): POUR(1,2)
广搜的时候需要判重，求出起始点到达终点的最短路径即所求：
当i=C或j=C时，就找到了

这里需要辅助数组记录队列内的值，类似于抓住那头牛的思路，以获得路径。
同时判重也需要标志数组进行判重。

当前版本：1.0
作    者：Louris
完成日期：2017.09.10
*/
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<deque>
#include<cmath>
using namespace std;
#define OK 1
#define ERROR 0
typedef int Status;
struct Node
{
	int i;
	int j;
	int father;//记录父节点位置
	int operators;//记录父节点的操作序
	Node(int ii, int jj, int ffather, int ooperators) :i(ii), j(jj), father(ffather), operators(ooperators) {};//赋值构造函数
	Node() {};//默认构造函数
};
int A, B, C;
vector<Node>v;
deque<Node>q;
int num;
Status Print_path(Node s)
{
	vector<Node>temp;
	temp.push_back(s);//终结点
	while (s.father != -1)
	{
		temp.push_back(v[s.father]);
		s = v[s.father];
	}
	cout << temp.size() - 1 << endl;
	for (vector<Node>::reverse_iterator rit = temp.rbegin() + 1; rit != temp.rend(); rit++)
	{
		switch (rit->operators)
		{
		case 1:
			cout << "FILL(1)" << endl;
			break;
		case 2:
			cout << "FILL(2)" << endl;
			break;
		case 3:
			cout << "DROP(1)" << endl;
			break;
		case 4:
			cout << "DROP(2)" << endl;
			break;
		case 5:
			cout << "POUR(2,1)" << endl;
			break;
		case 6:
			cout << "POUR(1,2)" << endl;
			break;
		}
	}
	return OK;
}
int main()
{
	while (cin >> A >> B >> C)
	{
		int Max = max(A, B);
		int * *visited = new int*[Max + 1];
		for (int i = 0; i < Max + 1; i++)
		{
			visited[i] = new int[Max + 1];
			fill(visited[i], visited[i] + Max + 1, 0);
		}
		//广搜
		num = -1;
		q.push_back(Node(0, 0, num, 0));
		v.push_back(Node(0, 0, num, 0));
		num++;
		while (!q.empty())
		{
			Node temp = q.front();
			if (temp.i == C || temp.j == C)
			{
				Print_path(temp);
				break;
			}
			else
			{
				for (int i = 1; i <= 6; i++)
				{
					switch (i)
					{
					case 1:
						if (visited[A][temp.j] != 1)
						{
							q.push_back(Node(A, temp.j, num, i));
							v.push_back(Node(A, temp.j, num, i));
							visited[A][temp.j] = 1;
						}
						break;
					case 2:
						if (visited[temp.i][B] != 1)
						{
							q.push_back(Node(temp.i, B, num, i));
							v.push_back(Node(temp.i, B, num, i));
							visited[temp.i][B] = 1;
						}
						break;
					case 3:
						if (visited[0][temp.j] != 1)
						{
							q.push_back(Node(0, temp.j, num, i));
							v.push_back(Node(0, temp.j, num, i));
							visited[0][temp.j] = 1;
						}
						break;
					case 4:
						if (visited[temp.i][0] != 1)
						{
							q.push_back(Node(temp.i, 0, num, i));
							v.push_back(Node(temp.i, 0, num, i));
							visited[temp.i][0] = 1;
						}
						break;
					case 5:
						if (temp.i + temp.j >= A)
						{
							if (visited[A][temp.i + temp.j - A] != 1)
							{
								q.push_back(Node(A, temp.i + temp.j - A, num, i));
								v.push_back(Node(A, temp.i + temp.j - A, num, i));
								visited[A][temp.i + temp.j - A] = 1;
							}
						}
						else
						{
							if (visited[temp.i + temp.j][0] != 1)
							{
								q.push_back(Node(temp.i + temp.j, 0, num, i));
								v.push_back(Node(temp.i + temp.j, 0, num, i));
								visited[temp.i + temp.j][0] = 1;
							}
						}
						break;
					case 6:
						if (temp.i + temp.j >= B)
						{
							if (visited[temp.i + temp.j - B][B] != 1)
							{
								q.push_back(Node(temp.i + temp.j - B, B, num, i));
								v.push_back(Node(temp.i + temp.j - B, B, num, i));
								visited[temp.i + temp.j - B][B] = 1;
							}
						}
						else
						{
							if (visited[0][temp.i + temp.j] != 1)
							{
								q.push_back(Node(0, temp.i + temp.j, num, i));
								v.push_back(Node(0, temp.i + temp.j, num, i));
								visited[0][temp.i + temp.j] = 1;
							}
						}
						break;
					}
				}
			}
			num++;
			q.pop_front();
		}
		if (q.empty())
		{
			cout << "impossible" << endl;
		}
		v.clear();
		q.clear();
		for (int i = 0; i < Max + 1; i++)
		{
			delete[] visited[i];
		}
		delete[] visited;
	}
	return 0;
}

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int OK = 1;
const int ERROR = 0;
typedef int Status;
struct CNode
{
	int i;
	int j;
	int father;//父节点位置
	int operators;//父节点操作序
	CNode(int ti,int tj,int tf,int to):i(ti),j(tj),father(tf),operators(to){};
	CNode(){};
};//状态
int A,B,C;
vector<CNode> v;
deque<CNode> dq;

Status Print_path(CNode s)
{
	vector<CNode> temp;
	while(s.father!=-1)
	{
		temp.push_back(s);
		s=v[s.father];
	}
	cout<<temp.size()<<endl;
	for(vector<CNode>::reverse_iterator rit=temp.rbegin();rit!=temp.rend();rit++)
	{
		switch(rit->operators)
		{
			case 0:
				cout<<"FILL(1)"<<endl;
				break;
			case 1:
				cout<<"FILL(2)"<<endl;
				break;
			case 2:
				cout<<"DROP(1)"<<endl;
				break;
			case 3:
				cout<<"DROP(2)"<<endl;
				break;
			case 4:
				cout<<"POUR(2,1)"<<endl;
				break;
			case 5:
				cout<<"POUR(1,2)"<<endl;
				break;
		}
	}
	return OK;
}
int main()
{
	while(cin>>A>>B>>C)
	{
		dq.clear();
		v.clear();
		dq.push_back(CNode(0,0,-1,-1));
		v.push_back(CNode(0,0,-1,-1));
		bool ** Visited=new bool*[max(A,B)+1];
		for(int i=0;i<max(A,B)+1;i++)
		{
			Visited[i]=new bool[max(A,B)+1];
			fill(Visited[i],Visited[i]+max(A,B)+1,false);
		}
		Visited[0][0]=true;
		int Index=0;
		while(!dq.empty())
		{
			CNode temp=dq.front();
			if(temp.i==C||temp.j==C)
			{
				Print_path(temp);
				break;
			}
			for(int i=0;i<6;i++)
			{
				switch(i)
				{
					case 0:
						if(!Visited[A][temp.j])
						{
							dq.push_back(CNode(A,temp.j,Index,i));
							v.push_back(CNode(A,temp.j,Index,i));
							Visited[A][temp.j]=true;
						}
						break;
					case 1:
						if(!Visited[temp.i][B])
						{
							dq.push_back(CNode(temp.i,B,Index,i));
							v.push_back(CNode(temp.i,B,Index,i));
							Visited[temp.i][B]=true;
						}
						break;
					case 2:
						if(!Visited[0][temp.j])
						{
							dq.push_back(CNode(0,temp.j,Index,i));
							v.push_back(CNode(0,temp.j,Index,i));
							Visited[0][temp.j]=true;
						}
						break;
					case 3:
						if(!Visited[temp.i][0])
						{
							dq.push_back(CNode(temp.i,0,Index,i));
							v.push_back(CNode(temp.i,0,Index,i));
							Visited[temp.i][0]=true;
						}
						break;
					case 4:
						if(temp.i+temp.j<=A)
						{
							if(!Visited[temp.i+temp.j][0])
							{
								dq.push_back(CNode(temp.i+temp.j,0,Index,i));
								v.push_back(CNode(temp.i+temp.j,0,Index,i));
								Visited[temp.i+temp.j][0]=true;
							}
						}
						else
						{
							if(!Visited[A][temp.i+temp.j-A])
							{
								dq.push_back(CNode(A,temp.i+temp.j-A,Index,i));
								v.push_back(CNode(A,temp.i+temp.j-A,Index,i));
								Visited[A][temp.i+temp.j-A]=true;
							}
						}
						break;
					case 5:
						if(temp.i+temp.j<=B)
						{
							if(!Visited[0][temp.i+temp.j])
							{
								dq.push_back(CNode(0,temp.i+temp.j,Index,i));
								v.push_back(CNode(0,temp.i+temp.j,Index,i));
								Visited[0][temp.i+temp.j]=true;
							}
						}
						else
						{
							if(!Visited[temp.i+temp.j-B][B])
							{
								dq.push_back(CNode(temp.i+temp.j-B,B,Index,i));
								v.push_back(CNode(temp.i+temp.j-B,B,Index,i));
								Visited[temp.i+temp.j-B][B]=true;
							}
						}
						break;
				}
			}
			Index++;//过一段时间重写一遍还是有效果的，王八蛋，这里居然傻到了！！！
			dq.pop_front();
		}
		if(dq.empty())
		{
			cout<<"impossible"<<endl;
		}
		for(int i=0;i<max(A,B)+1;i++)
		{
			delete[] Visited[i];
		}
		delete[] Visited;
	}
	return 0;
}

第七章散列(hash)

定义

元素通过一个函数转换为整数，使得该整数可以尽量唯一地代表这个元素
转换函数称为 散列函数H，也就是说，如果元素在转换前为key，那么转换后就是H(key)

整数散列

直接定制法

1.恒等变换：H(key)=Key
直接将key作为数组下标，是最常见最实用的散列应用
2.线性变换：H(key)=a*key+b

除留余数法

H(key)=key%mod
表长TSize不小于mod

冲突

通过除留余数法可能会有两个不同的数key1和key2，它们的hash值H(key)相同！

线性探查法（Linear Probing）——开放地址法

当得到的key的hash值H(key)，但是表中下标H(key)已经被占用，那么查找H(key)+1是否被占用，如果查找超过表长，则从表头重新开始查找，
知道找到一个可以使用的位置，或者是发现表中所有为之都已被使用。
容易导致扎堆，即表中连续若干个位置都被使用，这在一定程度上会降低效率

平方探查法（Quadratic probing）——开放地址法

H(key)+1^2, H(key)-1^2
H(key)+2^2, H(key)-2^2
…,
H(key)+k^2,H(key)-k^2
如果检查过程中H(key)+k^2超过了表长TSize，那么就把H(key)+k^2对表长TSize取模
如果检查过程中出现H(key)-k^2<0的情况（假设表的首位为0），那么将((H(key)-k^2)%TSize+Tsize)%TSize作为结果
如果想避免负数的麻烦，可以只进行正向的平方探查
可以证明，如果k在[0,TSize)范围内斗无法找到位置，那么当k>=TSize时，也一定无法找到位置。

链地址法——拉链法

和上面两种方法不同，链地址法不计算新的hash值，而是把所有H(key)相同的key连接成一条单链表。
这样可以设定一个数组Link，范围Link[0]~Link[mod-1]，其中Link[h]存放H(key)=h的一条单链表，于是当多个关键字key的hash值都是h时，就可以直接把这些冲突的key直接用单链表连接起来，此时就可以遍历这条单链表来寻找所有H(key)=h的key。

字符串hash初步

如果key不是整数，如何设计散列函数？
例如，将一个二维整点P的坐标映射成一个整数，可以用线性变换H(key)=x*Range+y

字符串只由大写字母A~Z构成

将A~~Z视为0~~25，那么对应26进制

int hashFunc(char S[],int len){
  int id=0;
  for(int i=0;i<len;i++){
    id=id*26+(S[i]-'A');
  }
  return id;
}

注意：字符串长度不能太长！

字符串包含了大小写字母

A~~Z视为0~~25，a~~z视为26~~51

int hashFunc(char S[],int len){
  int id=0;
  for(int i=0;i<len;i++){
    if(S[i]>='A'&&S[i]<='Z'){
      id=id*52+(S[i]-'A');
    }else if(S[i]>='a'&&S[i]<-'z'){
      id=id*52+S[i]-'a'+26 ;
    }
  }
  return id;
}

字符串包含大小写字母和数字

方法同上，只不过，最后直接在末尾加上对应数字即可，例如BCD4，731 4
还是用map吧！

第一章 枚举