算法笔记

简单模拟

【PAT B1001】害死人不偿命的（3n+1）猜想

卡拉兹(Callatz)猜想：
对任何一个自然数n，如果它是偶数，那么把它砍掉一半；如果它是奇数，那么把(3n+1)砍掉一半。这样一直反复砍下去，最后一定在某一步得到n=1。卡拉兹在1950年的世界数学家大会上公布了这个猜想，传说当时耶鲁大学师生齐动员，拼命想证明这个貌似很傻很天真的命题，结果闹得学生们无心学业，一心只证(3n+1)，以至于有人说这是一个阴谋，卡拉兹是在蓄意延缓美国数学界教学与科研的进展……
我们今天的题目不是证明卡拉兹猜想，而是对给定的任一不超过1000的正整数n，简单地数一下，需要多少步（砍几下）才能得到n=1？
输入格式
每个测试输入包含1个测试用例，即给出自然数n的值。
输出格式
输出从n计算到1需要的步数。
输入样例
3
输出样例
5
程序

#include<iostream>
using namespace std;

int main(){
	int n;
	int step;
	while(cin>>n){
		step=0;
		while(n!=1){
			if(n%2==0){
				n/=2;
			}else{
				n=(3*n+1)/2;
			}
			step++;
		}
		cout<<step<<endl;
	}
	return 0;
}

【PAT B1032】挖掘机技术哪家强

为了用事实说明挖掘机技术到底哪家强，PAT 组织了一场挖掘机技能大赛。现请你根据比赛结果统计出技术最强的那个学校。
输入格式
输入在第 1 行给出不超过 10
​5
​​ 的正整数 N，即参赛人数。随后 N 行，每行给出一位参赛者的信息和成绩，包括其所代表的学校的编号（从 1 开始连续编号）、及其比赛成绩（百分制），中间以空格分隔。
输出格式
在一行中给出总得分最高的学校的编号、及其总分，中间以空格分隔。题目保证答案唯一，没有并列。
输入样例
6
3 65
2 80
1 100
2 70
3 40
3 0
输出样例
2 150
程序

#include<iostream>
using namespace std;

const int MAX_SIZE=100000;
int schools[MAX_SIZE];
int main(){
	fill(schools,schools+MAX_SIZE,0);
	int number;
	int a,b;
	int maxSch,maxScore=0;
	cin>>number;
	while(number--){
		cin>>a>>b;
		schools[a]+=b;
		if(schools[a]>maxScore){
			maxScore=schools[a];
			maxSch=a;
		}
	}
	cout<<maxSch<<" "<<maxScore<<endl;
	return 0;
}

剩下的树

题目描述
有一个长度为整数L(1<=L<=10000)的马路，可以想象成数轴上长度为L的一个线段，起点是坐标原点，在每个整数坐标点有一棵树，即在0,1,2，…，L共L+1个位置上有L+1棵树。
现在要移走一些树，移走的树的区间用一对数字表示，如 100 200表示移走从100到200之间（包括端点）所有的树。
可能有M(1<=M<=100)个区间，区间之间可能有重叠。现在要求移走所有区间的树之后剩下的树的个数。
输入
两个整数L(1<=L<=10000)和M(1<=M<=100)。
接下来有M组整数，每组有一对数字。
输出
可能有多组输入数据，对于每组输入数据，输出一个数，表示移走所有区间的树之后剩下的树的个数。
样例输入
4 2
1 2
0 2
11 2
1 5
4 7
0 0
样例输出
2
5
程序

#include<iostream>
using namespace std;

const int MAX_SIZE=10001;
int trees[MAX_SIZE];
int main(){

	int L,M;
	while(cin>>L>>M&&(L>0&&M>0)){
		fill(trees,trees+L+1,1);//0~L（包括端点）区间初始化
		while(M--){
			int l,r;
			cin>>l>>r;
			for(int i=l;i<=r;i++){
				if(trees[i]>0){
					trees[i]--;
				}
			}
		}
		int num=0;
		for(int i=0;i<=L;i++){
			if(trees[i]>0){
				num++;
			}
		}
		cout<<num<<endl;
	}
	return 0;
}

A+B

题目描述
给定两个整数A和B，其表示形式是：从个位开始，每三位数用逗号”,”隔开。
现在请计算A+B的结果，并以正常形式输出。

输入
输入包含多组数据数据，每组数据占一行，由两个整数A和B组成（-10^9 < A,B < 10^9）。

输出
请计算A+B的结果，并以正常形式输出，每组数据占一行。

样例输入
-234,567,890 123,456,789
1,234 2,345,678
样例输出
-111111101
2346912
程序

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

int main(){
	string a,b;
	while(cin>>a>>b){
		long aa,bb;
		aa=bb=0;
		for(int i=0;i<a.length();i++){
			if(a[i]>='0'&&a[i]<='9'){
				aa=aa*10+a[i]-'0';
			}
		}
		if(a[0]=='-'){
			aa=-aa;
		}
		for(int i=0;i<b.length();i++){
			if(b[i]>='0'&&b[i]<='9'){
				bb=bb*10+b[i]-'0';
			}
		}
		if(b[0]=='-'){
			bb=-bb;
		}
		cout<<aa+bb<<endl;
	}
	return 0;
}

特殊乘法

题目描述
写个算法，对2个小于1000000000的输入，求结果。特殊乘法举例：123 * 45 = 1*4 +1*5 +2*4 +2*5 +3*4+3*5
输入
两个小于1000000000的数

输出
输入可能有多组数据，对于每一组数据，输出Input中的两个数按照题目要求的方法进行运算后得到的结果。

样例输入
24 65
42 66666
3 67
样例输出
66
180
39
程序

#include<iostream>
#include<cstring>
using namespace std;
int main(){
	string a,b;
	while(cin>>a>>b){
		int sum=0;
		for(int i=0;i<a.length();i++){
			for(int j=0;j<b.length();j++){
				sum+=(a[i]-'0')*(b[j]-'0');
			}
		}
		cout<<sum<<endl;
	}
	return 0;
}

比较奇偶数个数

题目描述
第一行输入一个数，为n，第二行输入n个数，这n个数中，如果偶数比奇数多，输出NO，否则输出YES。
输入
输入有多组数据。
每组输入n，然后输入n个整数（1<=n<=1000）。
输出
如果偶数比奇数多，输出NO，否则输出YES。
样例输入
1
67
7
0 69 24 78 58 62 64
样例输出
YES
NO
程序

#include<iostream>
#include<cmath>
using namespace std;
int main(){
	int n;
	while(cin>>n){
		int tmpN=n;
		int count=0; //偶数个数
		while(n--){
			int tmp;
			cin>>tmp;
			if(tmp%2==0){
				count++;
			}
		}
		if(count>=ceil(tmpN/2.0)){  //tmpN/2向上取整
			cout<<"NO"<<endl;
		}else{
			cout<<"YES"<<endl;
		}
	}
	return 0;
}

Shortest Distance

The task is really simple: given N exits on a highway which forms a simple cycle, you are supposed to tell the shortest distance between any pair of exits.
Input Specification
Each input file contains one test case. For each case, the first line contains an integer N (in [3, 105]), followed by N integer distances D1 D2 … DN, where Di is the distance between the i-th and the (i+1)-st exits, and DN is between the N-th and the 1st exits. All the numbers in a line are separated by a space. The second line gives a positive integer M (<=104), with M lines follow, each contains a pair of exit numbers, provided that the exits are numbered from 1 to N. It is guaranteed that the total round trip distance is no more than 107.
Output Specification
For each test case, print your results in M lines, each contains the shortest distance between the corresponding given pair of exits.
Sample Input
5 1 2 4 14 9
3
1 3
2 5
4 1
Sample Output
3
10
7
Procedure

/*
思路：
输入Di的时候记录a cycle的总距离cyDis
之后根据要求的两个exit的序号a,b（保证a比b小）
求a与b之间升序的各exit距离和sum，
与cyDis-sum（反向路程长）比较
输出二者中较小值。
*/
#include<iostream>
#include<cmath>
using namespace std;
int dis[100001];
int main(){
	int M,N;
	while(cin>>N){
		int cyDis=0;
		for(int i=1;i<=N;i++){
			cin>>dis[i];
			cyDis+=dis[i];
		}
		cin>>M;
		for(int i=0;i<M;i++){
			int a,b;
			cin>>a>>b;
			if(a>b) swap(a,b);
			int sum=0;
			for(int j=a;j<b;j++){
				sum+=dis[j];
			}
			if(sum>cyDis-sum){
				cout<<cyDis-sum<<endl;
			}else{
				cout<<sum<<endl;
			}
		}

	}
	return 0;
}

A+B和C

题目描述
给定区间$[-2^{31}, 2^{31}]$内的3个整数A、B和C，请判断A+B是否大于C。
输入
输入第1行给出正整数T(<=10)，是测试用例的个数。随后给出T组测试用例，每组占一行，顺序给出A、B和C。整数间以空格分隔。
输出
对每组测试用例，在一行中输出“Case #X: true”如果A+B>C，否则输出“Case #X: false”，其中X是测试用例的编号（从1开始）。
样例输入
4
1 2 3
2 3 4
2147483647 0 2147483646
0 -2147483648 -2147483647
样例输出
Case #1: false
Case #2: true
Case #3: true
Case #4: false
程序

#include<iostream>
#include<cstring>
using namespace std;
string result[2]={
	"false",
	"true"
};
int main(){
	int T;
	cin>>T;
	for(int i=1;i<=T;i++){
		long a,b,c; //int 2字节，long 4字节，long long 8字节 unsigned long 4字节
		cin>>a>>b>>c;
		cout<<"Case #"<<i<<": "<<result[a+b>c]<<endl;
	}
	return 0;
}

数字分类

题目描述
给定一系列正整数，请按要求对数字进行分类，并输出以下5个数字：
A1 = 能被5整除的数字中所有偶数的和；
A2 = 将被5除后余1的数字按给出顺序进行交错求和，即计算n1-n2+n3-n4…；
A3 = 被5除后余2的数字的个数；
A4 = 被5除后余3的数字的平均数，精确到小数点后1位；
A5 = 被5除后余4的数字中最大数字。
输入
每个输入包含1个测试用例。每个测试用例先给出一个不超过1000的正整数N，随后给出N个不超过1000的待分类的正整数。数字间以空格分隔。
输出
对给定的N个正整数，按题目要求计算A1~A5并在一行中顺序输出。数字间以空格分隔，但行末不得有多余空格。
若其中某一类数字不存在，则在相应位置输出“N”。
样例输入
13 1 2 3 4 5 6 7 8 9 10 20 16 18
8 1 2 4 5 6 7 9 16
样例输出
30 11 2 9.7 9
N 11 2 N 9
程序

#include<iostream>
#include<algorithm>
using namespace std;
struct Node{
	double x;
	bool exist;
};
Node A[6];
int main(){
	int N;
	while(cin>>N){
		int tmp;
		int a2=0;
		int a3=0;
		for(int i=0;i<6;i++){
			A[i].x=0;
			A[i].exist=false;
		}
		while(N--){
			cin>>tmp;
			switch(tmp%5){
				case 0:
					if(tmp%2==0){
						A[1].x+=tmp;
						A[1].exist=true;
					}
					 break;
				case 1:
					A[2].exist=true;
					A[2].x+=pow(-1,a2)*tmp;
					a2==0?a2=1:a2=0;
					break;
				case 2:
					A[3].exist=true;
					A[3].x++;
					break;
				case 3:
					A[4].exist=true;
					A[4].x+=tmp;
					a3++;
					break;
				case 4:
					A[5].exist=true;
					A[5].x=(A[5].x>tmp?A[5].x:tmp);
					break;
				default:break;
			}

		}
		if(a3!=0) A[4].x/=a3;
		for(int i=1;i<=5;i++){
			if(i!=1){
				cout<<" ";
			}
			if(A[i].exist){
				if(i!=4){
					printf("%0.f",A[i].x);
				}else{
					printf("%0.1f",A[i].x);
				}
			}else{
				cout<<"N";
			}
		}
		cout<<endl;
	}
	return 0;
}

部分A+B

题目描述
正整数A的“DA（为1位整数）部分”定义为由A中所有DA组成的新整数PA。例如：给定A = 3862767，DA = 6，则A的“6部分”PA是66，因为A中有2个6。
现给定A、DA、B、DB，请编写程序计算PA + PB。
输入
输入在一行中依次给出A、DA、B、DB，中间以空格分隔，其中0 < A, B < 1010。
输出
在一行中输出PA + PB的值。
样例输入
3862767 6 13530293 3
3862767 1 13530293 8
样例输出
399
0
程序

#include<iostream>
#include<cstring>
using namespace std;

int main(){
	string A,B;
	int DA,DB;

	while(cin>>A>>DA>>B>>DB){
		int aa=0;
		for(int i=0;i<A.length();i++){
			if(A[i]-'0'==DA){
				aa=aa*10+DA;
			}
		}
		int bb=0;
		for(int i=0;i<B.length();i++){
			if(B[i]-'0'==DB){
				bb=bb*10+DB;
			}
		}
		cout<<aa+bb<<endl;
	}
	return 0;
}

锤子剪刀布

现给出两人的交锋记录，请统计双方的胜、平、负次数，并且给出双方分别出什么手势的胜算最大。
输入格式
输入第1行给出正整数N（<=105），即双方交锋的次数。随后N行，每行给出一次交锋的信息，即甲、乙双方同时给出的的手势。C代表“锤子”、J代表“剪刀”、B代表“布”，第1个字母代表甲方，第2个代表乙方，中间有1个空格。
输出格式
输出第1、2行分别给出甲、乙的胜、平、负次数，数字间以1个空格分隔。第3行给出两个字母，分别代表甲、乙获胜次数最多的手势，中间有1个空格。如果解不唯一，则输出按字母序最小的解。
输入样例
10
C J
J B
C B
B B
B C
C C
C B
J B
B C
J J
输出样例
5 3 2
2 3 5
程序

#include<iostream>
#include<algorithm>
using namespace std;
struct Node{
	char ch;
	int sum;
};
bool cmp(Node a, Node b){
	if(a.sum==b.sum){
		return a.ch<b.ch;
	}else{
		return a.sum>b.sum;
	}
}
const char CH[3]={'C','J','B'};
int main(){

	int N;
	Node A[3],B[3];
	for(int i=0;i<3;i++){
		A[i].ch=CH[i];
		A[i].sum=0;
		B[i].ch=CH[i];
		B[i].sum=0;
	}
	while(cin>>N){
		int w,d,times;
		w=d=0;
		times=N;
		while(N--){
			char a,b;
			cin>>a>>b;
			if(a==b){   //平
				d++;
			}else{

				if(a=='C'&&b=='J'){
					w++;
					A[0].sum++;
				}
				if(a=='J'&&b=='B'){
					w++;
					A[1].sum++;
				}
				if(a=='B'&&b=='C'){
					w++;
					A[2].sum++;
				}
				if(a=='C'&&b=='B'){
					B[2].sum++;
				}
				if(a=='J'&&b=='C'){
					B[0].sum++;
				}
				if(a=='B'&&b=='J'){
					B[1].sum++;
				}
			}
		}
		cout<<w<<" "<<d<<" "<<times-w-d<<endl
			<<times-w-d<<" "<<d<<" "<<w<<endl;
		sort(A,A+3,cmp);
		sort(B,B+3,cmp);
		cout<<A[0].ch<<" "<<B[0].ch<<endl;
	}
	return 0;
}

查找元素

统计同成绩学生人数

题目描述
读入N名学生的成绩，将获得某一给定分数的学生人数输出。
输入
测试输入包含若干测试用例，每个测试用例的格式为

第1行：N
第2行：N名学生的成绩，相邻两数字用一个空格间隔。
第3行：给定分数

当读到N=0时输入结束。其中N不超过1000，成绩分数为（包含）0到100之间的一个整数。
输出
对每个测试用例，将获得给定分数的学生人数输出。
样例输入
4
70 80 90 100
80
3
65 75 85
55
5
60 90 90 90 85
90
0
样例输出
1
0
3
程序

#include<iostream>
using namespace std;

int main(){
	int N;
	while(cin>>N&&N!=0){
		int A[1001];
		for(int i=0;i<N;i++){
			cin>>A[i];
		}
		int tmp;
		int count=0;
		cin>>tmp;
		for(int i=0;i<N;i++){
			if(A[i]==tmp) count++;
		}
		cout<<count<<endl;
	}
	return 0;
}

找x

题目描述
输入一个数n，然后输入n个数值各不相同，再输入一个值x，输出这个值在这个数组中的下标（从0开始，若不在数组中则输出-1）。
输入
测试数据有多组，输入n(1<=n<=200)，接着输入n个数，然后输入x。
输出
对于每组输入,请输出结果。
样例输入
4
1 2 3 4
3
样例输出
2
程序

#include<iostream>
using namespace std;
int A[201];
int main(){
	int n;
	while(cin>>n){
		for(int i=0;i<n;i++){
			cin>>A[i];
		}
		int x;
		cin>>x;
		int i;
		for(i=0;i<n;i++){
			if(x==A[i]){
				cout<<i<<endl;
				break;
			}
		}
		if(i==n){
			cout<<-1<<endl;
		}

	}
	return 0;
}

查找学生信息

题目描述
输入N个学生的信息，然后进行查询。
输入
输入的第一行为N，即学生的个数(N<=1000)
接下来的N行包括N个学生的信息，信息格式如下：
01 李江 男 21
02 刘唐 男 23
03 张军 男 19
04 王娜 女 19
然后输入一个M(M<=10000),接下来会有M行，代表M次查询，每行输入一个学号，格式如下：
02
03
01
04
输出
输出M行，每行包括一个对应于查询的学生的信息。
如果没有对应的学生信息，则输出“No Answer!”
样例输入
5
001 张三 男 19
002 李四 男 20
003 王五 男 18
004 赵六 女 17
005 刘七 女 21
7
003
002
005
004
003
001
006
样例输出
003 王五 男 18
002 李四 男 20
005 刘七 女 21
004 赵六 女 17
003 王五 男 18
001 张三 男 19
No Answer!
程序

#include<iostream>
#include<cstring>
#include<map>
using namespace std;
struct Node{
	string name;
	string gender;
	int age;
	Node(){}
	Node(string Name,string Gender,int Age)
		:name(Name),gender(Gender),age(Age){}
	toString(){
		cout<<" "<<name<<" "<<gender<<" "<<age<<endl;
	}
};
map<string,Node> m;

int main(){
	int N,M;
	while(cin>>N){
		m.clear();
		for(int i=0;i<N;i++){
			string id,name,gender;
			int age;
			cin>>id>>name>>gender>>age;
			m[id]=Node(name,gender,age);
		}
		cin>>M;
		while(M--){
			string id;
			cin>>id;
			map<string,Node>::iterator it;
			it=m.find(id);
			if(it!=m.end()){
				cout<<it->first;
				it->second.toString();
			}else{
				cout<<"No Answer!"<<endl;
			}
		}
	}
	return 0;
}

查找

题目描述
输入数组长度 n
输入数组 a[1…n]
输入查找个数m
输入查找数字b[1…m]
输出 YES or NO 查找有则YES 否则NO 。
输入
输入有多组数据。
每组输入n，然后输入n个整数，再输入m，然后再输入m个整数（1<=m<=n<=100）。
输出
如果在n个数组中输出YES否则输出NO。
样例输入
6
3 2 5 4 7 8
2
3 6
样例输出
YES
NO
程序

#include<iostream>
#include<algorithm>
#include<set>
using namespace std;

int main(){
	int n;
	while(cin>>n){

		set<int> s;

		while(n--){
			int tmp;
			cin>>tmp;
			s.insert(tmp);
		}
		int m;
		cin>>m;
		while(m--){
			int tmp;
			cin>>tmp;
			if(s.find(tmp)!=s.end()){
				cout<<"YES"<<endl;
			}else{
				cout<<"NO"<<endl;
			}
		}
	}
	return 0;
}

图形输出

跟奥巴马一起编程

美国总统奥巴马不仅呼吁所有人都学习编程，甚至以身作则编写代码，成为美国历史上首位编写计算机代码的总统。2014 年底，为庆祝“计算机科学教育周”正式启动，奥巴马编写了很简单的计算机代码：在屏幕上画一个正方形。现在你也跟他一起画吧！
输入格式
输入在一行中给出正方形边长 N（3≤N≤20）和组成正方形边的某种字符 C，间隔一个空格。
输出格式
输出由给定字符 C 画出的正方形。但是注意到行间距比列间距大，所以为了让结果看上去更像正方形，我们输出的行数实际上是列数的 50%（四舍五入取整）。
输入样例
10 a
输出样例

aaaaaaaaaa
a        a
a        a
a        a
aaaaaaaaaa

程序

#include<iostream>
#include<string>
using namespace std;

int main(){
	int n;
	char c;
	while(cin>>n>>c){
		for(int i=0;i<n;i++) cout<<c;
		cout<<endl;
		int row=(int)(n/2.0+0.5);
		for(int i=1;i<row-1;i++){
			for(int j=0;j<n;j++){
				if(j==0||j==n-1){
					cout<<c;
				}else{
					cout<<" ";
				}
			}
			cout<<endl;
		}
		for(int i=0;i<n;i++) cout<<c;
		cout<<endl;
	}
	return 0;
}

Hello World for U

题目描述
Given any string of N (>=5) characters, you are asked to form the characters into the shape of U. For example, “helloworld” can be printed as:

h  d
e  l
l  r
lowo

That is, the characters must be printed in the original order, starting top-down from the left vertical line with n1 characters, then left to right along the bottom line with n2 characters, and finally bottom-up along the vertical line with n3 characters. And more, we would like U to be as squared as possible – that is, it must be satisfied that n1 = n3 = max { k| k <= n2 for all 3 <= n2 <= N } with n1 + n2 + n3 - 2 = N.
输入
Each input file contains one test case. Each case contains one string with no less than 5 and no more than 80 characters in a line. The string contains no white space.
输出
For each test case, print the input string in the shape of U as specified in the description.
样例输入
helloworld!
样例输出

h   !
e   d
l   l
lowor

程序

#include<iostream>
#include<cstring>
using namespace std;

int main(){
	string str;
	while(cin>>str){
		int len=str.length();
		int sideLen=(len+2)/3; //两列字符长
		int belowLen=len+2-2*sideLen; //底部字符长
		int front=0,rear=len-1;   //头尾指针
		for(int i=0;i<sideLen-1;i++){  //输出除底行外的所有行
			for(int j=0;j<belowLen;j++){
				if(j==0){
					cout<<str[front++];
				}else if(j==belowLen-1){
					cout<<str[rear--];
				}else{
					cout<<" ";
				}
			}
			cout<<endl;
		}
		while(front<=rear){  //输出底行
			cout<<str[front++];
		}
		cout<<endl;
	}
	return 0;
}

等腰梯形

题目描述
请输入高度h，输入一个高为h，上底边长为h的等腰梯形（例如h=4，图形如下）。

   ****
  ******
 ********
**********

输入
输入第一行表示样例数m，接下来m行每行一个整数h，h不超过10。
输出
对应于m个case输出要求的等腰梯形。
样例输入
1
4
样例输出

   ****
  ******
 ********
**********

程序

#include<iostream>
using namespace std;

int main(){
	int m;
	int h;
	cin>>m;
	while(m--){
		cin>>h;
		for(int i=1;i<=h;i++){
			for(int j=1;j<=h-i;j++){  //前缀空格
				cout<<" ";
			}
			for(int j=1;j<=h+2*(i-1);j++){ //输出字符
				cout<<"*";
			}
			cout<<endl;
		}
	}
	return 0;
}

沙漏图形

题目描述
问题：输入n，输出正倒n层星号三角形。首行顶格，星号间有一空格，效果见样例
输入样例
3
输出样例

* * *
 * *
  *
 * *
* * *

程序

#include<iostream>
using namespace std;

int main(){
	int n;
	while(cin>>n){
		for(int i=0;i<n;i++){  //上半区，包括中间行
			for(int k=0;k<i;k++) cout<<" "; //前缀空格
			for(int j=0;j<n-i;j++){
				if(j!=0) cout<<" ";
				cout<<"*";
			}
			cout<<endl;
		}
		for(int i=n-2;i>=0;i--){ //下半区，不包括中间行
			for(int k=0;k<i;k++) cout<<" "; //前缀空格
			for(int j=0;j<n-i;j++){
				if(j!=0) cout<<" ";
				cout<<"*";
			}
			cout<<endl;
		}
	}
	return 0;
}

日期处理

日期差值

题目描述
有两个日期，求两个日期之间的天数，如果两个日期是连续的我们规定他们之间的天数为两天。
输入
有多组数据，每组数据有两行，分别表示两个日期，形式为YYYYMMDD
输出
每组数据输出一行，即日期差值
样例输入
20130101
20130105
样例输出
5
程序

#include<iostream>
#include<cstring>
using namespace std;
const int MONTH[2][13]={
	0,31,28,31,30,31,30,31,31,30,31,30,31, //非闰年各月天数
	0,31,29,31,30,31,30,31,31,30,31,30,31  //闰年各月天数
};
bool isLeap(int year){
	if((year%4==0&&year%100!=0)||(year%400==0)){
		return true;
	}
	return false;
}
int main(){
	string date1,date2;
	while(cin>>date1>>date2){
		if(date1>date2) swap(date1,date2);
		cout<<date1<<" "<<date2<<endl;
		int year1,year2;
		int month1,month2;
		int day1,day2;
		year1=(date1[0]-'0')*1000+(date1[1]-'0')*100+(date1[2]-'0')*10+date1[3]-'0';
		year2=(date2[0]-'0')*1000+(date2[1]-'0')*100+(date2[2]-'0')*10+date2[3]-'0';

		month1=(date1[4]-'0')*10+date1[5]-'0';
		month2=(date2[4]-'0')*10+date2[5]-'0';

		day1=(date1[6]-'0')*10+date1[7]-'0';
		day2=(date2[6]-'0')*10+date2[7]-'0';

		int sumDays=0;
		if(year1==year2){
			if(month1==month2){

				//month1(month2)
				sumDays=day2-day1+1;
			}else{
				//month1
				int index=isLeap(year1);
				sumDays+=MONTH[index][month1]-day1+1;

				//month1+1~month2-1
				for(int month=month1+1;month<month2;month++){
					sumDays+=MONTH[index][month];
				}

				//month2
				sumDays+=day2;
			}
		}else{
			//year1
			int index=isLeap(year1);
			sumDays+=MONTH[index][month1]-day1+1;
			for(int month=month1+1;month<=12;month++){
				sumDays+=MONTH[index][month];
			}

			//year1+1~year2-1
			for(int year=year1+1;year<year2;year++){
				if(isLeap(year)){
					sumDays+=366;
				}else{
					sumDays+=365;
				}
			}

			//year2
			index=isLeap(year2);
			for(int month=1;month<month2;month++){
				sumDays+=MONTH[index][month];
			}
			sumDays+=day2;
		}
		cout<<sumDays<<endl;
	}
	return 0;
}

Day of week

题目描述
We now use the Gregorian style of dating in Russia. The leap years are years with number divisible by 4 but not divisible by 100, or divisible by 400.
For example, years 2004, 2180 and 2400 are leap. Years 2004, 2181 and 2300 are not leap.
Your task is to write a program which will compute the day of week corresponding to a given date in the nearest past or in the future using today’s agreement about dating.
输入
There is one single line contains the day number d, month name M and year number y(1000≤y≤3000). The month name is the corresponding English name starting from the capital letter.
输出
Output a single line with the English name of the day of week corresponding to the date, starting from the capital letter. All other letters must be in lower case.
样例输入
21 December 2012
5 January 2013
样例输出
Friday
Saturday
程序

#include<iostream>
#include<cstring>

#include<map>
#include<vector>
using namespace std;
const int monthDays[2][13]={
	0,31,28,31,30,31,30,31,31,30,31,30,31, //非闰年各月天数
	0,31,29,31,30,31,30,31,31,30,31,30,31  //闰年各月天数
};
map<string,int> monthMap;
const string dayName[7]={
	"Sunday",
	"Monday",
	"Tuesday",
	"Wednesday",
	"Thursday",
	"Friday",
	"Saturday"
};

bool isLeap(int year){
	if((year%4==0&&year%100!=0)||(year%400==0)){
		return true;
	}
	return false;
}

const int YEAR=2012;
const int MONTH=12;
const int DAY=21;
const int dayWeek=5;

int main(){

	monthMap["January"]=1;
	monthMap["February"]=2;
	monthMap["March"]=3;
	monthMap["April"]=4;
	monthMap["May"]=5;
	monthMap["June"]=6;
	monthMap["July"]=7;
	monthMap["August"]=8;
	monthMap["September"]=9;
	monthMap["Octember"]=10;
	monthMap["November"]=11;
	monthMap["December"]=12;

	int day,year;
	string month;
	while(cin>>day>>month>>year){
		int sumDays=0;
		int year1=YEAR,year2=year;
		int month1=MONTH,month2=monthMap[month];
		int day1=DAY,day2=day;

		//保证year1与year2对应日期大者在后
		if(year1>year2){
			swap(year1,year2);
			swap(month1,month2);
			swap(day1,day2);
		}else if(year1==year2) {
			if(month1>month2){
				swap(month1,month2);
				swap(day1,day2);
			}else if(month1==month2){
				if(day1>day2){
					swap(day1,day2);
				}
			}
		}

		if(year1==year2){
			if(month1==month2){

				//month1(month2)
				sumDays=day2-day1+1;
			}else{
				//month1
				int index=isLeap(year1);
				sumDays+=monthDays[index][month1]-day1+1;

				//month1+1~month2-1
				for(int month=month1+1;month<month2;month++){
					sumDays+=monthDays[index][month];
				}

				//month2
				sumDays+=day2;
			}
		}else{
			//year1
			int index=isLeap(year1);
			sumDays+=monthDays[index][month1]-day1+1;
			for(int month=month1+1;month<=12;month++){
				sumDays+=monthDays[index][month];
			}

			//year1+1~year2-1
			for(int year=year1+1;year<year2;year++){
				if(isLeap(year)){
					sumDays+=366;
				}else{
					sumDays+=365;
				}
			}

			//year2
			index=isLeap(year2);
			for(int month=1;month<month2;month++){
				sumDays+=monthDays[index][month];
			}
			sumDays+=day2;
		}
		sumDays--; //原先计算值是两日期之差，包含两日期在内

		int rest=(sumDays+dayWeek)%7;

		cout<<dayName[rest]<<endl;
	}
	return 0;
}

打印日期

题目描述
给出年分m和一年中的第n天，算出第n天是几月几号。
输入
输入包括两个整数y(1<=y<=3000)，n(1<=n<=366)。
输出
可能有多组测试数据，对于每组数据，按 yyyy-mm-dd的格式将输入中对应的日期打印出来。
样例输入
2013 60
2012 300
2011 350
2000 211
样例输出
2013-03-01
2012-10-26
2011-12-16
2000-07-29
程序

#include<iostream>
using namespace std;
const int monthDays[2][13]={
	0,31,28,31,30,31,30,31,31,30,31,30,31, //非闰年各月天数
	0,31,29,31,30,31,30,31,31,30,31,30,31  //闰年各月天数
};
bool isLeap(int year){
	if((year%4==0&&year%100!=0)||(year%400==0)){
		return true;
	}
	return false;
}
int main(){
	int year,n;
	while(cin>>year>>n){
		int sumDays=0;
		int index=isLeap(year);
		for(int month=1;month<=12;month++){
			if(n-sumDays>=monthDays[index][month]){
				sumDays+=monthDays[index][month];
			}else{
				if(n-sumDays==0){
					printf("%04d-%02d-%02d\n",year,month-1,monthDays[index][month-1]);
				}else{
					printf("%04d-%02d-%02d\n",year,month,n-sumDays);
				}
				break;
			}
		}
	}
	return 0;
}

日期类

题目描述
编写一个日期类，要求按xxxx-xx-xx 的格式输出日期，实现加一天的操作。
输入
输入第一行表示测试用例的个数m，接下来m行每行有3个用空格隔开的整数，分别表示年月日。测试数据不会有闰年。
输出
输出m行。按xxxx-xx-xx的格式输出，表示输入日期的后一天的日期。
样例输入
2
1999 10 20
2001 1 31
样例输出
1999-10-21
2001-02-01
程序

#include<iostream>
using namespace std;

class Date{
	public:
		Date(){}
		Date(int Year,int Month,int Day):year(Year),month(Month),day(Day){}
		void addOneDay();
		void printfNextDay()const;

	private:
		int year;
		int month;
		int day;
		const int monthDays[2][13]={
			{0,31,28,31,30,31,30,31,31,30,31,30,31}, //非闰年各月天数
			{0,31,29,31,30,31,30,31,31,30,31,30,31}  //闰年各月天数
		};
		bool isLeap(int year){
			if((year%4==0&&year%100!=0)||(year%400==0)){
				return true;
			}
			return false;
		}
};
void Date::addOneDay(){
	int index=isLeap(this->year);
	int days=this->day+1;
	if(days>monthDays[index][this->month]){
		this->day=1;
		this->month=(this->month+1)%13;
		if(this->month==0){
			this->month=1;
			this->year++;
		}

	}else{
		this->day++;
	}
}
void Date::printfNextDay()const{
	printf("%04d-%02d-%02d\n",this->year,this->month,this->day);
}
int main(){
	int n;
	cin>>n;

	while(n--){
		int year,month,day;
		cin>>year>>month>>day;
		Date date(year,month,day);
		date.addOneDay();
		date.printfNextDay();
	}
	return 0;
}

日期累加

题目描述
设计一个程序能计算一个日期加上若干天后是什么日期。
输入
输入第一行表示样例个数m，接下来m行每行四个整数分别表示年月日和累加的天数。
输出
输出m行，每行按yyyy-mm-dd的个数输出。
样例输入
1
2008 2 3 100
样例输出
2008-05-13
程序

#include<iostream>

using namespace std;
const int monthDays[2][13]={
	{0,31,28,31,30,31,30,31,31,30,31,30,31}, //the number of days per months in a non-leap year
	{0,31,29,31,30,31,30,31,31,30,31,30,31}  //the number of days per month in a leap year
};
bool isLeap(int year){ //Judge whether the parameter 'year' is the leap year.
	if((year%4==0&&year%100!=0)||(year%400==0)){
		return true;
	}
	return false;
}
int main(){
	int n;
	cin>>n;
	while(n--){
		int year,month,day,days;
		cin>>year>>month>>day>>days;
		int index=isLeap(year);
		if(day+days<=monthDays[index][month]){ //The final date is still within this month.
			printf("%04d-%02d-%02d\n",year,month,day+days);
		}else{
			days-=monthDays[index][month]-day; //Subtract the remainning days of the month.

			month=(month+1)%13;         //Note that month must be between 1 and 12
			if(month==0){				//Arrive the next year
				year++;
				month=1;
			}

			while(days>=monthDays[index][month]){ //Substract all Full-Month days
				days-=monthDays[index][month];

				month=(month+1)%13;   //As above
				if(month==0){
					year++;
					month=1;
				}
			}

			if(days==0){   //It happens to be the last day of a month
				month--;
				if(month==0){
					month=12;
					year--;
				}
				printf("%04d-%02d-%02d\n",year,month,monthDays[index][month]);
			}else{  //The day of a month except the last day
				printf("%04d-%02d-%02d\n",year,month,days);
			}
		}
	}
	return 0;
}

进制转换

又一版A+B

题目描述
输入两个不超过整型定义的非负10进制整数A和B($<=2^{31}-1$)，输出A+B的m (1 < m < 10)进制数。
输入
输入格式：测试输入包含若干测试用例。每个测试用例占一行，给出m和A，B的值。
当m为0时输入结束。
输出
输出格式：每个测试用例的输出占一行，输出A+B的m进制数。
样例输入
2 4 5
8 123 456
0
样例输出
1001
1103
程序

#include<iostream>
#include<vector>
using namespace std;

int main(){
	long long m,a,b;

	//Use Class Vector instead of Class Stack
	//beacause Class Stack don't have the member function "void clear();"
	//that can clear up all elements of the stack.
	vector<long long> vec;  
	while(cin>>m&&m!=0){
		cin>>a>>b;
		vec.clear();
		a+=b;
		if(a==0) vec.push_back(a); //The special situation of a
		while(a!=0){   //Convert base
			int tmp=a%m;
			vec.push_back(tmp);
			a/=m;
		}
		vector<long long>::reverse_iterator rit;   //Output the elements of Vector in reverse order
		for(rit=vec.rbegin();rit!=vec.rend();rit++){
			cout<<*rit;
		}
		cout<<endl;
	}
	return 0;
}

数制转换

题目描述
求任意两个不同进制非负整数的转换（2进制～16进制），所给整数在long所能表达的范围之内。
不同进制的表示符号为（0，1，…，9，a，b，…，f）或者（0，1，…，9，A，B，…，F）。
输入
输入只有一行，包含三个整数a，n，b。a表示其后的n 是a进制整数，b表示欲将a进制整数n转换成b进制整数。a，b是十进制整数，2 =< a，b <= 16。
输出
可能有多组测试数据，对于每组数据，输出包含一行，该行有一个整数为转换后的b进制数。输出时字母符号全部用大写表示，即（0，1，…，9，A，B，…，F）。
样例输入
4 123 10
样例输出
27
程序

#include<iostream>
#include<cstring>
#include<cmath>
#include<vector>
using namespace std;
const char BASE[16]={'0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F'};
int main(){
	long a,b;
	string n;
	vector<long> vec;
	vector<char> res;
	while(cin>>a>>n>>b){
		long result;
		vec.clear();
		res.clear();

		for(int i=0;i<n.length();i++){  //'a' radix converts to '10' radix.
			result+=(n[i]-'0')*pow(a,n.length()-i-1);
		}

		if(result==0) vec.push_back(result);  //The special situation of result
		while(result!=0){              //'10' radix converts to 'b' radix.
			long tmp=result%b;
			vec.push_back(tmp);
			result/=b;
		}

		for(int i=0;i<vec.size();i++){
			res.push_back(BASE[vec[i]]);
		}
		for(int i=vec.size()-1;i>=0;i--){
			cout<<res[i];
		}
		cout<<endl;
	}
	return 0;
}

进制转换

题目描述
将一个长度最多为30位数字的十进制非负整数转换为二进制数输出。
输入
多组数据，每行为一个长度不超过30位的十进制非负整数。
（注意是10进制数字的个数可能有30个，而非30bits的整数）
输出
每行输出对应的二进制数。
样例输入
985
211
1126
样例输出
1111011001
11010011
10001100110
程序

#include<iostream>
#include<cstring>
#include<stack>
using namespace std;

int main(){
	string str;
	while(cin>>str){
		stack<int>s;
		int count=0;
		//The loop will end when each character of the parameter 'str' of Class String
		//becomes the same character '0'.
		while(count!=str.length()){  
			count=0;
			int rest=0;
			for(int i=0;i<str.length();i++){  //Simulte the process of integer's division
				int tmp=rest;
				rest=(rest*10+str[i]-'0')%2;
				str[i]=(tmp*10+str[i]-'0')/2+'0';
				if(str[i]=='0'){
					count++;      //Flag that records the state of every character of the parameter 'str'
				}			
			}
			s.push(rest);
		}
		//Output the binary result, first input last output.
		while(!s.empty()){
			cout<<s.top();
			s.pop();
		}
		cout<<endl;
	}
	return 0;
}

八进制

题目描述
输入一个整数，将其转换成八进制数输出。
输入
输入包括一个整数N(0<=N<=100000)。
输出
可能有多组测试数据，对于每组数据，
输出N的八进制表示数。
样例输入
9
8
5
样例输出
11
10
5
程序

#include<iostream>
#include<stack>
using namespace std;

int main(){
	int n;
	while(cin>>n){
		stack<int>s;
		if(n==0) s.push(n); //The special situation of n
		while(n){
			s.push(n%8);
			n/=8;
		}
		while(!s.empty()){
			cout<<s.top();
			s.pop();
		}
		cout<<endl;
	}
	return 0;
}

字符串处理

字符串连接

题目描述
不借用任何字符串库函数实现无冗余地接受两个字符串，然后把它们无冗余的连接起来。
输入
每一行包括两个字符串，长度不超过100。
输出
可能有多组测试数据，对于每组数据，
不借用任何字符串库函数实现无冗余地接受两个字符串，然后把它们无冗余的连接起来。
输出连接后的字符串。
样例输入
abc def
样例输出
abcdef
程序

#include<iostream>

using namespace std;
const int MAX=101;
char ch1[MAX],ch2[MAX];
int main(){
	while(cin>>ch1>>ch2){
		int index1=0;
		while(ch1[index1]!='\0') ++index1;
		int index2=0;
		while(ch2[index2]!='\0'){
			ch1[index1++]=ch2[index2++];
		}
		ch1[index1]='\0';
		cout<<ch1<<endl;
	}
	return 0;
}

首字母大写

题目描述
对一个字符串中的所有单词，如果单词的首字母不是大写字母，则把单词的首字母变成大写字母。
在字符串中，单词之间通过空白符分隔，空白符包括：空格(’ ‘)、制表符(‘\t’)、回车符(‘\r’)、换行符(‘\n’)。
输入
输入一行：待处理的字符串（长度小于100）。
输出
可能有多组测试数据，对于每组数据，
输出一行：转换后的字符串。
样例输入
if so, you already have a google account. you can sign in on the right.
样例输出
If So, You Already Have A Google Account. You Can Sign In On The Right.
程序

#include<iostream>
#include<cstring>
#include<cctype>
using namespace std;

int main(){
	string str;
	while(getline(cin,str)){
		char pre=' ';
		int index=0;
		while(str[index]!='\0'){
			if(pre==' '||pre=='\t'||pre=='\r'||pre=='\n'){ //Judge whether the previous character is one of the Blank Characters.
				if(str[index]>='a'&&str[index]<='z'){
					str[index]=str[index]+'A'-'a';
				}
			}
			pre=str[index];
			index++;
		}
		cout<<str<<endl;
	}
	return 0;
}

字符串的查找删除

题目描述
给定一个短字符串（不含空格），再给定若干字符串，在这些字符串中删除所含有的短字符串。
输入
输入只有1组数据。
输入一个短字符串（不含空格），再输入若干字符串直到文件结束为止。
输出
删除输入的短字符串(不区分大小写)并去掉空格,输出。
样例输入

in
#include
int main()
{
  printf(" Hi ");
}

程序

#include<iostream>
#include<cstring>
using namespace std;
string sample;
string str;
bool judge(int l,int r){
	if(sample[l]==str[r])
		return true;
	return false;
}
int main(){

	cin>>sample;
	getchar(); //Erase line feeds
	while(getline(cin,str)){
		while(str.find(sample)!=string::npos){ //Erase all specified strings in the string
			int index=str.find(sample);
			str.erase(index,sample.length());
		}
		while(str.find(" ")!=string::npos){  //Erase all white spaces in the string
			int index=str.find(" ");
			str.erase(index,1);
		}
		cout<<str<<endl;
	}
	return 0;
}

单词替换

题目描述
输入一个字符串，以回车结束（字符串长度<=100）。该字符串由若干个单词组成，单词之间用一个空格隔开，所有单词区分大小写。现需要将其中的某个单词替换成另一个单词，并输出替换之后的字符串。
输入
多组数据。每组数据输入包括3行，
第1行是包含多个单词的字符串 s，
第2行是待替换的单词a，(长度<=100)
第3行是a将被替换的单词b。(长度<=100)

s, a, b 最前面和最后面都没有空格。
输出
每个测试数据输出只有 1 行，
将s中所有单词a替换成b之后的字符串。
样例输入
I love Tian Qin
I
You
样例输出
You love Tian Qin
程序

#include<iostream>
#include<cstring>
using namespace std;
string str,src,dst;
/*
 Warning: note the differences among the functions 'find()' and 'find_first_of()'
*/
int main(){
	while(getline(cin,str)){
		getline(cin,src);
		getline(cin,dst);
		cout<<str<<":"<<endl<<src<<":"<<dst<<":"<<endl;
		int index=str.find(src,0);
		while(index!=string::npos){
			if( (index==0||str[index-1]==' ')
			    &&
				(str[index+src.length()]==' '||str[index+src.length()]=='\0')
			  ){  
			    //The specified word which can be replaced
			    //may be between two white spaces,
			    //the first word of the sentence,
			    //or the last word of the sentence.

				str.replace(index,src.length(),dst); //Replace the specified word

				index=str.find(src,index+dst.length());  //Resume to find next word

			}else{
			    //find the location of next word
				index=str.find(' ',index);
				if(index!=string::npos)
					index=str.find(src,index);

			}

		}
		cout<<str<<endl;
	}
	return 0;
}

字符串中去特定字符

题目描述
输入字符串s和字符c，要求去掉s中所有的c字符，并输出结果。
输入
测试数据有多组，每组输入字符串s和字符c。
输出
对于每组输入,输出去除c字符后的结果。
样例输入
goaod
a
样例输出
good
程序

#include<iostream>
#include<cstring>
using namespace std;

int main(){

	string str;
	char ch;
	while(getline(cin,str)){
    cin>>ch;
		while(str.find(ch)!=string::npos){
			int index=str.find(ch);
			str.erase(index,1);
		}
		cout<<str<<endl;
	}
	return 0;
}

数组逆置

题目描述
输入一个字符串，长度小于等于200，然后将数组逆置输出。
输入
测试数据有多组，每组输入一个字符串。
输出
对于每组输入,请输出逆置后的结果。
样例输入
tianqin
样例输出
niqnait
程序

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

int main(){
	string str;
	while(getline(cin,str)){
		reverse(str.begin(),str.end());
		cout<<str<<endl;
	}
	return 0;
}

比较字符串

题目描述
输入两个字符串，比较两字符串的长度大小关系。
输入
输入第一行表示测试用例的个数m，接下来m行每行两个字符串A和B，字符串长度不超过50。
输出
输出m行。若两字符串长度相等则输出A is equal long to B；若A比B长，则输出A is longer than B；否则输出A is shorter than B。
样例输入
2
abc xy
bbb ccc
样例输出
abc is longer than xy
bbb is equal long to ccc
程序

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

int main(){
	int n;
	string a,b;
	cin>>n;
	while(n--){
		cin>>a>>b;
		if(a.length()<b.length()){
			swap(a,b);
		}
		if(a.length()==b.length()){
			cout<<a<<" is equal long to "<<b<<endl;
		}else{
			cout<<a<<" is longer than "<<b<<endl;
		}
	}
	return 0;
}

编排字符串

题目描述
请输入字符串，最多输入4 个字符串，要求后输入的字符串排在前面，例如
输入：EricZ
输出：1=EricZ
输入：David
输出：1=David 2=EricZ
输入：Peter
输出：1=Peter 2=David 3=EricZ
输入：Alan
输出：1=Alan 2=Peter 3=David 4=EricZ
输入：Jane
输出：1=Jane 2=Alan 3=Peter 4=David
输入
第一行为字符串个数m，接下来m行每行一个字符床，m不超过100，每个字符床长度不超过20。
输出
输出m行，每行按照样例格式输出，注意用一个空格隔开。
样例输入
5
EricZ
David
Peter
Alan
Jane
样例输出
1=EricZ
1=David 2=EricZ
1=Peter 2=David 3=EricZ
1=Alan 2=Peter 3=David 4=EricZ
1=Jane 2=Alan 3=Peter 4=David
程序

#include<iostream>
#include<cstring>
#include<vector>
using namespace std;

int main(){
	int m;
	string str;
	vector<string> vec;
	cin>>m;
	while(m--){
		cin>>str;
		vec.push_back(str);

		int index=1;
		for(int i=vec.size()-1;i>=0&&index<=4;i--){
			if(i!=vec.size()-1) cout<<" ";
			cout<<index++<<"="<<vec[i];
		}
		cout<<endl;
	}
	return 0;
}

回文串

题目描述
读入一串字符，判断是否是回文串。“回文串”是一个正读和反读都一样的字符串，比如“level”或者“noon”等等就是回文串。
输入
一行字符串，长度不超过255。
输出
如果是回文串，输出“YES”，否则输出“NO”。
样例输入
12321
样例输出
YES
程序

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

int main(){
	string str;
	while(cin>>str){
		string tmp=str;
		reverse(tmp.begin(),tmp.end());
		if(tmp==str){
			cout<<"YES"<<endl;
		}else{
			cout<<"NO"<<endl;
		}
	}
	return 0;
}

排序

排序

题目描述
对输入的n个数进行排序并输出。
输入
输入的第一行包括一个整数n(1<=n<=100)。 接下来的一行包括n个整数。
输出
可能有多组测试数据，对于每组数据，将排序后的n个整数输出，每个数后面都有一个空格。
每组测试数据的结果占一行。
样例输入
5
5 4 3 1 2
样例输出
1 2 3 4 5
程序

#include<iostream>
#include<functional>
#include<vector>
#include<algorithm>
using namespace std;
int main(){
	int n;
	while(cin>>n){
		vector<int> vec;
		while(n--){
			int tmp;
			cin>>tmp;
			vec.push_back(tmp);
		}
		sort(vec.begin(),vec.end(),less<int>());
		vector<int>::iterator it;
		for(it=vec.begin();it!=vec.end();it++){
			if(it!=vec.begin()) cout<<" ";
			cout<<*it;
		}
		cout<<endl;
	}
	return 0;
}

特殊排序

题目描述
输入一系列整数，将其中最大的数挑出，并将剩下的数进行排序。
输入
输入第一行包括1个整数N，1<=N<=1000，代表输入数据的个数。
接下来的一行有N个整数。
输出
可能有多组测试数据，对于每组数据，
第一行输出一个整数，代表N个整数中的最大值，并将此值从数组中去除，将剩下的数进行排序。
第二行将排序的结果输出。
样例输入
5
5 3 2 4 1
样例输出
5
1 2 3 4
提示
如果数组中只有一个数，当第一行将其输出后，第二行请输出”-1”。
程序

#include<iostream>
#include<algorithm>
#include<vector>
#include<functional>
using namespace std;

int main(){
	int n;
	while(cin>>n){
		vector<int> vec;
		while(n--){
			int tmp;
			cin>>tmp;
			vec.push_back(tmp);
		}
		sort(vec.begin(),vec.end(),less<int>());
		cout<<vec[vec.size()-1]<<endl;
		for(vector<int>::iterator it=vec.begin();it!=--vec.end();it++){
			if(it!=vec.begin()) cout<<" ";
			cout<<*it;
		}
		if(vec.size()==1){
			cout<<"-1";
		}
		cout<<endl;
	}
	return 0;
}

Excel排序

题目描述
Excel可以对一组纪录按任意指定列排序。现请你编写程序实现类似功能。
对每个测试用例，首先输出1行“Case i:”，其中 i 是测试用例的编号（从1开始）。随后在 N 行中输出按要求排序后的结果，即：当 C=1 时，按学号递增排序；当 C=2时，按姓名的非递减字典序排序；当 C=3 时，按成绩的非递减排序。当若干学生具有相同姓名或者相同成绩时，则按他们的学号递增排序。
输入
测试输入包含若干测试用例。每个测试用例的第1行包含两个整数 N (N<=100000) 和 C，其中 N 是纪录的条数，C 是指定排序的列号。以下有N行，每行包含一条学生纪录。每条学生纪录由学号（6位数字，同组测试中没有重复的学号）、姓名（不超过8位且不包含空格的字符串）、成绩（闭区间[0, 100]内的整数）组成，每个项目间用1个空格隔开。当读到 N=0 时，全部输入结束，相应的结果不要输出。
输出
对每个测试用例，首先输出1行“Case i:”，其中 i 是测试用例的编号（从1开始）。随后在 N 行中输出按要求排序后的结果，即：当 C=1 时，按学号递增排序；当 C=2时，按姓名的非递减字典序排序；当 C=3 时，按成绩的非递减排序。当若干学生具有相同姓名或者相同成绩时，则按他们的学号递增排序。
样例输入
4 1
000001 Zhao 75
000004 Qian 88
000003 Li 64
000002 Sun 90
4 2
000005 Zhao 95
000011 Zhao 75
000007 Qian 68
000006 Sun 85
4 3
000002 Qian 88
000015 Li 95
000012 Zhao 70
000009 Sun 95
0 3
样例输出
Case 1:
000001 Zhao 75
000002 Sun 90
000003 Li 64
000004 Qian 88
Case 2:
000007 Qian 68
000006 Sun 85
000005 Zhao 95
000011 Zhao 75
Case 3:
000012 Zhao 70
000002 Qian 88
000009 Sun 95
000015 Li 95
程序

#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
struct Student{
	string id;     //Student ID
	string name;   //Student Name
	int score;     //Student Score
	int item;      //Sort Item that represents the different sort means
	Student(){}    //Default Consructor
	Student(string ID,string Name,int Score,int Item)  //Custom Constructor
	:id(ID),name(Name),score(Score),item(Item){}

	bool operator <(const Student b) const{ //Comparing Operator Rewriting
		bool result=false;

		switch(item){  //Select a particular sort method based on 'item'
			case 1:{   //Base on 'id'
				result=this->id<b.id;
				break;
			}

			case 2:{   //Base on 'name' when two students have different names
				if(this->name!=b.name){
					result=this->name<b.name;
				}else{
					result=this->id<b.id;
				}
				break;
			}
			case 3:{   //Base on 'score when two students have different scores
				if(this->score!=b.score){
					result=this->score<b.score;
				}else{
					result=this->id<b.id;
				}
				break;
			}
		}
		return result;
	}
	void toString(){  //Print the information
		std::cout<<id<<" "<<name<<" "<<score<<std::endl;
	}
};

int main(){
	string id,name;
	int score;
	int n,item;
	int nCase=0;
	while(cin>>n>>item&&n!=0){
		nCase++;
		vector<Student> vec;
		//Input data
		while(n--){
			cin>>id>>name>>score;
			vec.push_back(Student(id,name,score,item));
		}

		//Sort data
		sort(vec.begin(),vec.end());

		//Print data
		cout<<"Case "<<nCase<<":"<<endl;
		vector<Student>::iterator it;
		for(it=vec.begin();it!=vec.end();it++){				
			it->toString();
		}
	}
	return 0;
}

字符串内排序

题目描述
输入一个字符串，长度小于等于200，然后将输出按字符顺序升序排序后的字符串。
输入
测试数据有多组，输入字符串。
输出
对于每组输入,输出处理后的结果。
样例输入
tianqin
样例输出
aiinnqt
程序

#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
#include<string>
#include<functional>
using namespace std;
int main() {
	string str;
	while (getline(cin, str)) {
		sort(str.begin(), str.end(),less<char>());
		cout << str << endl;
		str.clear();
	}
	return 0;
}

Problem B

题目描述
请写一个程序，对于一个m行m列的（1<m<10）的方阵，求其每一行，每一列及主对角线元素之和，最后按照从大到小的顺序依次输出。
输入
共一组数据，输入的第一行为一个正整数，表示m，接下来的m行，每行m个整数表示方阵元素。
输出
从大到小排列的一行整数，每个整数后跟一个空格，最后换行。
样例输入
4
15 8 -2 6
31 24 18 71
-3 -9 27 13
17 21 38 69
样例输出
159 145 144 135 81 60 44 32 28 27
程序

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<functional>
using namespace std;
int main(){
	int n;
	cin>>n;

	//Parameters that respectively represents the sum of each row, column, diagnal line
	int *row,*col,*diag;
	row=new int[n];
	col=new int[n];
	diag=new int[2];

	//Initiate all arrays
	fill(row,row+n,0);
	fill(col,col+n,0);
	fill(diag,diag+2,0);

	//Input
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			int tmp;
			cin>>tmp;
			row[i]+=tmp;
			col[j]+=tmp;
			if(i==j) diag[0]+=tmp;
			if(i+j==n-1) diag[1]+=tmp;
		}
	}

	//Vector used to sort all data
	vector<int> vec;
	for(int i=0;i<n;i++){
		vec.push_back(row[i]);
		vec.push_back(col[i]);
	}
	vec.push_back(diag[0]);
	vec.push_back(diag[1]);
	sort(vec.begin(),vec.end(),greater<int>());

	//Output
	for(vector<int>::iterator it=vec.begin();it!=vec.end();it++){
		cout<<*it<<" ";
	}
	cout<<endl;

	//Free memory
	delete [] row;
	delete [] col;
	delete [] diag;
	return 0;
}

小白鼠排队

题目描述
N只小白鼠(1 <= N <= 100)，每只鼠头上戴着一顶有颜色的帽子。现在称出每只白鼠的重量，要求按照白鼠重量从大到小的顺序输出它们头上帽子的颜色。帽子的颜色用“red”，“blue”等字符串来表示。不同的小白鼠可以戴相同颜色的帽子。白鼠的重量用整数表示。
输入
多案例输入，每个案例的输入第一行为一个整数N，表示小白鼠的数目。
下面有N行，每行是一只白鼠的信息。第一个为不大于100的正整数，表示白鼠的重量，；第二个为字符串，表示白鼠的帽子颜色，字符串长度不超过10个字符。
注意：白鼠的重量各不相同。
输出
每个案例按照白鼠的重量从大到小的顺序输出白鼠的帽子颜色。
样例输入
1
79 omi
9
46 lcg
92 cru
37 ceq
54 vhr
17 wus
27 tnv
13 kyr
95 wld
34 qox
样例输出
omi
wld
cru
vhr
lcg
ceq
qox
tnv
wus
kyr
程序

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
#include<string>
#include<functional>
using namespace std;
struct Mouse {
	int heavy;
	string color;
	Mouse(int h, string c) {
		heavy = h;
		color = c;
	}
	bool operator < (const Mouse & m)const {
		return heavy > m.heavy;
	}
};
int main() {
	int n;
	vector<Mouse> vec;
	while (cin >> n) {
		vec.clear();
		for (int i = 0; i < n; i++) {
			int h;
			string str;
			cin >> h >> str;
			vec.push_back(Mouse(h, str));
		}
		sort(vec.begin(), vec.end());
		for (vector<Mouse>::iterator it = vec.begin(); it != vec.end(); it++) {
			cout << it->color << endl;
		}
	}
	return 0;
}

中位数

题目描述
中位数定义：一组数据按从小到大的顺序依次排列，处在中间位置的一个数（或最中间两个数据的平均数）.
给出一组无序整数，求出中位数，如果求最中间两个数的平均数，向下取整即可（不需要使用浮点数）
输入
该程序包含多组测试数据，每一组测试数据的第一行为N，代表该组测试数据包含的数据个数，1<=N<=10000.
接着N行为N个数据的输入，N=0时结束输入
输出
输出中位数，每一组测试数据输出一行
样例输入
1
468
15
501
170
725
479
359
963
465
706
146
282
828
962
492
996
943
0
样例输出
468
501

#include<iostream>
#include<cstring>
#include<string>
#include<vector>
#include<algorithm>
#include<functional>
using namespace std;
int main() {
	int n;
	vector<double> vec;
	while (cin >> n&&n!=0) {
		vec.clear();
		for (int i = 0; i < n; i++) {
			double temp;
			cin >> temp;
			vec.push_back(temp);
		}
		sort(vec.begin(), vec.end());
		if ((n & 1) == 0) {
			cout << floor((vec[n / 2] + vec[n / 2 - 1])/2) << endl;
		}
		else {
			cout << vec[n / 2] << endl;
		}
	}
	return 0;
}

##整数奇偶排序

题目描述
输入10个整数，彼此以空格分隔。重新排序以后输出(也按空格分隔)，要求:
1.先输出其中的奇数,并按从大到小排列；
2.然后输出其中的偶数,并按从小到大排列。
输入
任意排序的10个整数（0～100），彼此以空格分隔。
输出
可能有多组测试数据，对于每组数据，按照要求排序后输出，由空格分隔。
样例输入
0 56 19 81 59 48 35 90 83 75
17 86 71 51 30 1 9 36 14 16
样例输出
83 81 75 59 35 19 0 48 56 90
71 51 17 9 1 14 16 30 36 86

#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<functional>
#include<vector>
using namespace std;
int main() {
	int flag = 0;
	int x;
	vector<int> vecA, vecB;
	while (cin >> x) {
		flag++;
		if ((x & 1) != 0) {
			vecA.push_back(x);
		}
		else {
			vecB.push_back(x);
		}
		if (flag % 10 == 0) {
			flag = 0;
			sort(vecA.begin(), vecA.end(), greater<int>());
			sort(vecB.begin(), vecB.end(), less<int>());
			for (vector<int>::iterator it = vecA.begin(); it != vecA.end(); it++) {
				cout << *it << " ";
			}
			for (vector<int>::iterator it = vecB.begin(); it != vecB.end(); it++) {
				cout << *it;
				if (it != vecB.end() - 1) {
					cout << " ";
				}
			}
			cout << endl;
			vecA.clear();
			vecB.clear();
		}
	}
	return 0;
}

排名

题目描述
今天的上机考试虽然有实时的Ranklist，但上面的排名只是根据完成的题数排序，没有考虑每题的分值，所以并不是最后的排名。给定录取分数线，请你写程序找出最后通过分数线的考生，并将他们的成绩按降序打印。
输入
测试输入包含若干场考试的信息。每场考试信息的第1行给出考生人数N ( 0 < N < 1000 )、考题数M ( 0 < M < = 10 )、分数线（正整数）G；第2行排序给出第1题至第M题的正整数分值；以下N行，每行给出一名考生的准考证号（长度不超过20的字符串）、该生解决的题目总数m、以及这m道题的题号（题目号由1到M）。
当读入的考生人数为0时，输入结束，该场考试不予处理。
输出
对每场考试，首先在第1行输出不低于分数线的考生人数n，随后n行按分数从高到低输出上线考生的考号与分数，其间用1空格分隔。若有多名考生分数相同，则按他们考号的升序输出。
样例输入
3 5 32
17 10 12 9 15
CS22003 5 1 2 3 4 5
CS22004 3 5 1 3
CS22002 2 1 5
0
样例输出
3
CS22003 63
CS22004 44
CS22002 32

#include<iostream>
#include<algorithm>
#include<functional>
#include<cstring>
#include<string>
#include<vector>
using namespace std;
struct Node {
	string id;
	int score;
	Node(string Id, int Score) {
		id = Id;
		score = Score;
	}
	Node() {}
	bool operator < (const Node & s) const {
		return score > s.score;
	}
};
vector<Node> vec;
vector<Node> result;
vector<int> nQuestion;
int main() {
	int n, m, g;
	while (cin >> n >> m >> g && n != 0) {
		vec.clear();
		result.clear();
		nQuestion.clear();
		for (int i = 0; i < m; i++) {
			int temp;
			cin >> temp;
			nQuestion.push_back(temp);
		}
		for (int i = 0; i < n; i++) {
			string id;
			int x;
			cin >> id >> x;
			vec.push_back(Node(id, 0));
			for (int j = 0; j < x; j++) {
				int temp;
				cin >> temp;
				vec[i].score += nQuestion[temp - 1];
			}
		}
		sort(vec.begin(), vec.end());
		for (vector<Node>::iterator it = vec.begin(); it != vec.end(); it++) {
			if (it->score >= g) {
				result.push_back(*it);
			}
		}
		cout << result.size() << endl;
		for (vector<Node>::iterator it = result.begin(); it != result.end(); it++) {
			cout << it->id << " " << it->score << endl;
		}
	}
	return 0;
}

谁是你的潜在朋友

题目描述
“臭味相投”——这是我们描述朋友时喜欢用的词汇。两个人是朋友通常意味着他们存在着许多共同的兴趣。然而作为一个宅男，你发现自己与他人相互了解的机会 并不太多。幸运的是，你意外得到了一份北大图书馆的图书借阅记录，于是你挑灯熬夜地编程，想从中发现潜在的朋友。
首先你对借阅记录进行了一番整理，把N个读者依次编号为1,2,…,N，把M本书依次编号为1,2,…,M。同时，按照“臭味相投”的原则，和你喜欢读同一本书的人，就是你的潜在朋友。你现在的任务是从这份借阅记录中计算出每个人有几个潜在朋友。

输入
每个案例第一行两个整数N,M，2 <= N ，M<= 200。接下来有N行，第i(i = 1,2,…,N)行每一行有一个数，表示读者i-1最喜欢的图书的编号P(1<=P<=M)

输出
每个案例包括N行，每行一个数，第i行的数表示读者i有几个潜在朋友。如果i和任何人都没有共同喜欢的书，则输出“BeiJu”（即悲剧，^ ^）

样例输入
4 5
2
3
2
1
样例输出
1
BeiJu
1
BeiJu

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;

vector<int> vec; //The array records the data of books that everyone likes.
int hashTable[201];    //The array records the sum of each book.
int main() {
	int n, m;
	while (cin >> n >> m) {
		vec.resize(n,0); //Initiate the vector
		fill(hashTable,hashTable+201,0); //as above
		for(int i=0;i<n;i++){
			int temp;
			cin>>temp;
			vec[i]=temp;
			hashTable[temp]++;
		}
		for(int i=0;i<n;i++){
			if(hashTable[vec[i]]<2){
				cout<<"BeiJu"<<endl;
			}else{
				cout<<hashTable[vec[i]]-1<<endl;
			}
		}
	}
	return 0;
}

分组统计

题目描述
先输入一组数，然后输入其分组，按照分组统计出现次数并输出，参见样例。
输入
输入第一行表示样例数m，对于每个样例，第一行为数的个数n，接下来两行分别有n个数，第一行有n个数，第二行的n个数分别对应上一行每个数的分组，n不超过100。
输出
输出m行，格式参见样例，按从小到大排。
样例输入
1
7
3 2 3 8 8 2 3
1 2 3 2 1 3 1
样例输出
1={2=0,3=2,8=1}
2={2=1,3=0,8=1}
3={2=1,3=1,8=0}

#include<iostream>
#include<algorithm>
#include<set>
#include<vector>
#include<map>
using namespace std;
multiset<int> Link[101];
vector<int> vec;
set<int> noMulti;
set<int>  Set;
int main() {
	int m;
	cin >> m;
	while (m--) {
		int n;
		vec.clear();
		noMulti.clear();
		Set.clear();
		for (int i = 0; i < 101; i++) {
			Link[i].clear();
		}
		cin >> n;
		for (int i = 0; i < n; i++) {
			int temp;
			cin >> temp;
			Set.insert(temp);
			vec.push_back(temp);
		}
		for (int i = 0; i < n; i++) {
			int temp;
			cin >> temp;
			Link[temp].insert(vec[i]);
			noMulti.insert(temp);
		}
		for (set<int>::iterator it = noMulti.begin(); it != noMulti.end(); it++) {
			cout << *it << "={";
			for (set<int>::iterator its = Set.begin(); its != Set.end(); its++) {
				cout << *its << "=" << Link[*it].count(*its);
				if (its != --Set.end()) {
					cout << ",";
				}
			}
			cout << "}" << endl;
		}
	}
	return 0;
}

Be Unique

题目描述
Being unique is so important to people on Mars that even their lottery is designed in a unique way. The rule of winning is simple: one bets on a number chosen from [1, 104]. The first one who bets on a unique number wins. For example, if there are 7 people betting on 5 31 5 88 67 88 17, then the second one who bets on 31 wins.
输入
Each input file contains one test case. Each case contains a line which begins with a positive integer N (<=105) and then followed by N bets. The numbers are separated by a space.
输出
For each test case, print the winning number in a line. If there is no winner, print “None” instead.
样例输入
7 5 31 5 88 67 88 17
5 888 666 666 888 888
样例输出
31
None

#include<iostream>
#include<algorithm>
#include<vector>
#include<set>
using namespace std;

//Method 1:
//Hash
/*const int MAX_SIZE=10001;
int isUnique[MAX_SIZE];
vector<int> vec;
int main() {
	int n;
	while(cin>>n){
		vec.resize(n,0);
		fill(isUnique,isUnique+MAX_SIZE,0);
		for(int i=0;i<n;i++){
			cin>>vec[i];
			isUnique[vec[i]]++;
		}
		bool isExist=false;
		for(int i=0;i<n;i++){
			if(isUnique[vec[i]]==1){
				isExist=true;
				cout<<vec[i]<<endl;
				break;
			}
		}
		if(!isExist){
			cout<<"None"<<endl;
		}
	}
	return 0;
}*/

//Method 2:
//MultiSet
multiset<int> mulSet;
vector<int> vec;
int main(){
	int n;
	while(cin>>n){
		vec.resize(n,0);
		mulSet.clear();
		for(int i=0;i<n;i++){
			cin>>vec[i];
			mulSet.insert(vec[i]);
		}
		bool isExist=false;
		for(int i=0;i<n;i++){
			if(mulSet.count(vec[i])==1){
				cout<<vec[i]<<endl;
				isExist=true;
				break;
			}
		}
		if(!isExist){
			cout<<"None"<<endl;
		}
	}
	return 0;
}

String Subtraction

题目描述
Given two strings S1 and S2, S = S1 - S2 is defined to be the remaining string after taking all the characters in S2 from S1. Your task is simply to calculate S1 - S2for any given strings. However, it might not be that simple to do it fast.
输入
Each input file contains one test case. Each case consists of two lines which gives S1 and S2, respectively. The string lengths of both strings are no more than 104. It is guaranteed that all the characters are visible ASCII codes and white space, and a new line character signals the end of a string.
输出
For each test case, print S1 - S2 in one line.
样例输入
They are students.
aeiou
样例输出
Thy r stdnts.

#include<iostream>
#include<cstring>
#include<set>
using namespace std;
string s1,s2;
int main(){
	//Get the two strings
	//Function 'getline()' can get all characters of a line except the 'Enter' key
	//Because the 'Enter' key is the flag that distinguishs the different lines
	while(getline(cin,s1),getline(cin,s2)){

		//Erase all repetitive characters in s2
		set<char> s;
		for(int i=0;i<s2.length();i++){  
			s.insert(s2[i]);
		}
		//Erase all characters in s2 from s1
		for(set<char>::iterator it=s.begin();it!=s.end();it++){
			while(s1.find(*it)!=string::npos){
				s1.erase(s1.find(*it),1);
			}
		}
		//print the result
		cout<<s1<<endl;
	}
	return 0;
}

递归

吃糖果

题目描述
名名的妈妈从外地出差回来，带了一盒好吃又精美的巧克力给名名（盒内共有 N 块巧克力，20 > N >0）。
妈妈告诉名名每天可以吃一块或者两块巧克力。
假设名名每天都吃巧克力，问名名共有多少种不同的吃完巧克力的方案。
例如：
如果N=1，则名名第1天就吃掉它，共有1种方案；
如果N=2，则名名可以第1天吃1块，第2天吃1块，也可以第1天吃2块，共有2种方案；
如果N=3，则名名第1天可以吃1块，剩2块，也可以第1天吃2块剩1块，所以名名共有2+1=3种方案；
如果N=4，则名名可以第1天吃1块，剩3块，也可以第1天吃2块，剩2块，共有3+2=5种方案。
现在给定N，请你写程序求出名名吃巧克力的方案数目。
输入
输入只有1行，即整数N。
输出
可能有多组测试数据，对于每组数据，
输出只有1行，即名名吃巧克力的方案数。
样例输入
1
2
4
样例输出
1
2
5
程序

#include<iostream>
#include<algorithm>
using namespace std;

/*
Thinking:
Recurrence formula:
f[n]=f[n-1]+f[n-2];
f[0]=1;
f[1]=1;
f[2]=f[1]+f[0]=2;
f[3]=f[2]+f[1]=3
f[4]=f[3]+f[2]=5
*/

//Method 1:
//Recursion
/*int Recursion(int n){
	if(n==0||n==1){
		return 1;
	}else{
		return Recursion(n-1)+Recursion(n-2);
	}
}
int main(){
	int n;
	while(cin>>n){
		cout<<Recursion(n)<<endl;
	}
	return 0;
}*/

//Method 2:
//Dynamic Programming
int DP[21];
int main(){
	int n;
	while(cin>>n){
		DP[0]=DP[1]=1;
		for(int i=2;i<=n;i++){
			DP[i]=DP[i-1]+DP[i-2];
		}
		cout<<DP[n]<<endl;
	}
	return 0;
}

数列

题目描述
编写一个求斐波那契数列的递归函数，输入n 值，使用该递归函数，输出如下图形（参见样例）。
输入
输入第一行为样例数m，接下来有m行每行一个整数n，n不超过10。
输出
对应每个样例输出要求的图形(参见样例格式)。
1
样例输入
6
样例输出

          0
        0 1 1
      0 1 1 2 3
    0 1 1 2 3 5 8
  0 1 1 2 3 5 8 13 21
0 1 1 2 3 5 8 13 21 34 55

程序

#include<iostream>
using namespace std;
int Fib[21];
int main(){
	int m;
	cin>>m;
	while(m--){
		int n;
		cin>>n;
		Fib[0]=0;
		Fib[1]=Fib[2]=1;
		for(int i=3;i<=2*(n-1);i++){
			Fib[i]=Fib[i-1]+Fib[i-2];
		}
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n-i;j++) cout<<"  "; //前缀空格
			for(int j=0;j<=2*(i-1);j++){
				if(j!=0) cout<<" ";
				cout<<Fib[j];
			}
			cout<<endl;
		}
	}
	return 0;
}

神奇的口袋

题目描述
有一个神奇的口袋，总的容积是40，用这个口袋可以变出一些物品，这些物品的总体积必须是40。John现在有n个想要得到的物品，每个物品的体积分别是a1，a2……an。John可以从这些物品中选择一些，如果选出的物体的总体积是40，那么利用这个神奇的口袋，John就可以得到这些物品。现在的问题是，John有多少种不同的选择物品的方式。
输入
输入的第一行是正整数n (1 <= n <= 20)，表示不同的物品的数目。接下来的n行，每行有一个1到40之间的正整数，分别给出a1，a2……an的值。
输出
输出不同的选择物品的方式的数目。
样例输入
2
12
28
3
21
10
5
样例输出
1
0
程序

#include<iostream>
#include<algorithm>
using namespace std;

//Thinking:
//Recurrence formula: good a[i] acquired or discarded
//f(40,n)=f(40-a[i],n-1)+f(40,n-1)
//f(0,x)=1; space fills up
//f(x,0)=0; There's room left but all goods have been selected
//f(-x,n)=0; Insufficient space

////Method 1:
////Recursion
//int a[21];
//int n;
//int selected(int space,int item){
//	if(space==0) return 1;	//Stop recursion when space reaches zero, and get one approach
//	if(space<0)  return 0;  //Insufficient space
//	if(item<=0)  return 0;  //End of selection
//	return selected(space -a[item],item-1)+selected(space,item-1);
//}
//int main(){
//	while(cin>>n){
//	 	for(int i=1;i<=n;i++) cin>>a[i];
//	 	cout<<selected(40,n)<<endl;
//	}
//	return 0;
//}

//Method 2:
//Dynamic Programming
int a[21];
int DP[41][21];
int main(){
	int n;
	while(cin>>n){
		for(int i=0;i<21;i++) DP[0][i]=1;
		for(int i=1;i<41;i++) DP[i][0]=0;
		for(int i=1;i<=n;i++) cin>>a[i];
		for(int i=1;i<=40;i++){
			for(int j=1;j<=n;j++){
				if(i-a[j]<0) DP[i][j]=DP[i][j-1];
				else DP[i][j]=DP[i-a[j]][j-1]+DP[i][j-1];
			}
		}
		cout<<DP[40][n]<<endl;
	}
	return 0;
}

八皇后

题目描述
会下国际象棋的人都很清楚：皇后可以在横、竖、斜线上不限步数地吃掉其他棋子。如何将8个皇后放在棋盘上（有8 * 8个方格），使它们谁也不能被吃掉！这就是著名的八皇后问题。
对于某个满足要求的8皇后的摆放方法，定义一个皇后串a与之对应，即a=b1b2…b8，其中bi为相应摆法中第i行皇后所处的列数。已经知道8皇后问题一共有92组解（即92个不同的皇后串）。
给出一个数b，要求输出第b个串。串的比较是这样的：皇后串x置于皇后串y之前，当且仅当将x视为整数时比y小。
输入
第1行是测试数据的组数n，后面跟着n行输入。每组测试数据占1行，包括一个正整数b(1 <= b <= 92)
输出
输出有n行，每行输出对应一个输入。输出应是一个正整数，是对应于b的皇后串。
样例输入
3
6
4
25
样例输出
25713864
17582463
36824175
程序

#include<iostream>
#include<cstring>
#include<vector>
#include<string>
#include<algorithm>
#include<cmath>
#include<functional>
using namespace std;
typedef int Status;
const int OK=1;
const int ERROR=0;
vector<string> vResult; //Result Set
string temp;            //Procedure Variable
bool bVisited[9];       //An array of tags used to distinguish different columns
Status Recursion(int n){
	if(n==9){  //Results
		vResult.push_back(temp);
		return OK;
	}
	for(int i=1;i<=8;i++){
		if(!bVisited[i]){  //Different columns
			bool flag=true;  //Mark different diagonals
			for(int j=0;j<temp.size();j++){
				if(abs(temp[j]-'0'-i)==abs(j+1-n)){
					flag=false;
					break;
				}
			}
			if(flag){ //Different diggonals
				//Record data
				bVisited[i]=true;
				temp+=i+'0';
				Recursion(n+1); //Next line
				//Recover
				temp.erase(temp.size()-1,1);
				bVisited[i]=false;
			}

		}
	}
	return ERROR;
}

int main(){
	//Initialize array, perform recursive operations and sort the results
	fill(bVisited,bVisited+9,false);
	Recursion(1);
	sort(vResult.begin(),vResult.end(),less<string>());

	//Input sampels and return target results
	int n;
	cin>>n;
	while(n--){
		int tmp;
		cin>>tmp;		
		cout<<vResult[tmp-1]<<endl;
	}
	return 0;
}

贪心

看电视

题目描述
暑假到了，小明终于可以开心的看电视了。但是小明喜欢的节目太多了，他希望尽量多的看到完整的节目。
现在他把他喜欢的电视节目的转播时间表给你，你能帮他合理安排吗？
输入
输入包含多组测试数据。每组输入的第一行是一个整数n（n<=100），表示小明喜欢的节目的总数。
接下来n行，每行输入两个整数si和ei（1<=i<=n），表示第i个节目的开始和结束时间，为了简化问题，每个时间都用一个正整数表示。
当n=0时，输入结束。
输出
对于每组输入，输出能完整看到的电视节目的个数。
样例输入
12
1 3
3 4
0 7
3 8
15 19
15 20
10 15
8 18
6 12
5 10
4 14
2 9
0
样例输出
5
程序

#include<iostream>
#include<algorithm>
#include<vector>
#include<functional>
using namespace std;
/*
Thinking：
Interval Greedy
Sort the intervals from small to large according to the right end points of them:
Select the intervals one by one whose right end point is smaller
*/

struct Program{
	int sTime;
	int eTime;
	Program(){}
	Program(int sT,int eT):sTime(sT),eTime(eT){}
	bool operator < (const Program &tmp) const{
		return eTime<tmp.eTime;
	}
};

vector<Program> vec;
int main(){
	int n;
	while(cin>>n&&n!=0){
		vec.resize(n); //Resize the vector
		for(int i=0;i<n;i++){   //Input data
			cin>>vec[i].sTime>>vec[i].eTime;
		}
		sort(vec.begin(),vec.end()); //Sort the data
		int lastEndTime=0;  //The end-time of the last program which we can choose
		int nCount=0;      //the number of programs
		for(int i=0;i<n;i++){ //Calculate
			if(vec[i].sTime>=lastEndTime){
				nCount++;
				lastEndTime=vec[i].eTime;
			}
		}
		cout<<nCount<<endl;
	}
	return 0;
}

出租车费

题目描述
某市出租车计价规则如下：起步4公里10元，即使你的行程没超过4公里；接下来的4公里，每公里2元；之后每公里2.4元。行程的最后一段即使不到1公里，也当作1公里计费。
一个乘客可以根据行程公里数合理安排坐车方式来使自己的打车费最小。
例如，整个行程为16公里，乘客应该将行程分成长度相同的两部分，每部分花费18元，总共花费36元。如果坐出租车一次走完全程要花费37.2元。
现在给你整个行程的公里数，请你计算坐出租车的最小花费。

输入
输入包含多组测试数据。每组输入一个正整数n（n<10000000），表示整个行程的公里数。
当n=0时，输入结束。
输出
对于每组输入，输出最小花费。如果需要的话，保留一位小数。
样例输入
3
9
16
0
样例输出
10
20.4
36
程序

#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;

/*
Thinking:
We should pay attemtion to the need to  minimize the cost per kilometer.
Distance-Interval  Unit-Price  Total-Price
4                  2.5          10
4                  2            8
~                  2.4          ~

Distance > 8:
- 8~13,   Continue the journey without changing the taxi
- >13,    Restart the journey and charge after the taxi travels eight kilometers,
          because the unit-price per kilometer is lower than the one without changing the taxi

*/
int main(){
	int distance;
	while(cin>>distance&&distance!=0){
		double sum=0;
		while(distance!=0){
			if(distance<=13){
				if(distance<=4) sum+=10;
				else if(distance<=8) sum+=10+2*(distance-4);
				else sum+=18+2.4*(distance-8);
				distance=0;
			}else{
				sum+=18;
				distance-=8;
			}
		}
		if(floor(sum)<sum) printf("%.1f\n",sum);
		else printf("%d\n",(int)sum);
	}
	return 0;
}

To Fill or Not to Fill

With highways available, driving a car from Hangzhou to any other city is easy. But since the tank capacity of a car is limited, we have to find gas stations on the way from time to time. Different gas station may give different price. You are asked to carefully design the cheapest route to go.
Input Specification
Each input file contains one test case. For each case, the first line contains 4 positive numbers: Cmax (≤ 100), the maximum capacity of the tank; D (≤30000), the distance between Hangzhou and the destination city; Davg(≤20), the average distance per unit gas that the car can run; and N (≤ 500), the total number of gas stations. Then N lines follow, each contains a pair of non-negative numbers: P
​i, the unit gas price, and Di(≤D), the distance between this station and Hangzhou, for i=1,⋯,N. All the numbers in a line are separated by a space.
Output Specification
For each test case, print the cheapest price in a line, accurate up to 2 decimal places. It is assumed that the tank is empty at the beginning. If it is impossible to reach the destination, print The maximum travel distance = X where X is the maximum possible distance the car can run, accurate up to 2 decimal places.
Sample Input 1
50 1300 12 8
6.00 1250
7.00 600
7.00 150
7.10 0
7.20 200
7.50 400
7.30 1000
6.85 300
Sample Output 1
749.17
Sample Input 2
50 1300 12 2
7.10 0
7.00 600
Sample Output 2
The maximum travel distance = 1200.00
Procedure

#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<vector>
#include<cmath>
#include<functional>
using namespace std;
/*
Thinking:
Greedy:
The price we cost must be the cheapest from HangZhou to the destination.
Supposed that we are at 'A' gas station now, choose the specific one among the reachable gas stations:
1. No station we can reach: we cann't arrive at the destination
2. There is not one gas station whose unit-price is lower than the current statioon:
   Fill the tank up
3. There are some stations whose unit-price is lower than the current station:
   Reach the nearest gas station

Note:
Cann't select the one whose unit-price is the lowest among the reachable gas stations, consider the following:
Station  Unit-Price Distance
1         3          10
2         2          20
3         1          30
~
Now, we are at the 1 station, and we can reach the 2 and 3 station.
Obviously, 3 station is the one whose unit-price is the lowest.
But we cann't select it arbitrarily:
Supposed that the rest oil in the tank can support us to reach the 1 station, of couse, we can select it.
However, if not that, we should choose the 2 station because we must lower the price per kilometer.
*/
const int INF=0x3f3f3f;
double capacity;     //The maximum capacity of the tank
double dstDis;       //The distance between HangZhou and the destination city
double avgDis;       //The average distance per unit gas that the car can run
int nStation;        //the total number of gas stations
double minPrice;     //The cheapest price
double maxDis;       //The maximum distance the taxi can run

//Gas station
struct Station{
	double price;
	double distance;
	Station(){}      //Default Constructor
	Station(double Price,double Distance):price(Price),distance(Distance){}   //Parametric Constructor
	bool operator < (const Station & tmp) const{
		return distance<tmp.distance;
	}
};

vector<Station> vecStation;  //The vector records the data of each gas station

int main(){

	while(cin>>capacity>>dstDis>>avgDis>>nStation){

		//Initialize data
		vecStation.resize(nStation+1);
		minPrice=maxDis=0;
		for(int i=0;i<nStation;i++){
			cin>>vecStation[i].price>>vecStation[i].distance;
		}

		vecStation[nStation].price=0;
		vecStation[nStation].distance=dstDis;

		//Sort the elements in the vector 'vec'
		sort(vecStation.begin(),vecStation.end(),less<Station>());

		//Exceptional case
		if(vecStation[0].distance!=0){
			printf("The maximum travel distance = %.2f\n",0);
			continue;
		}

		int nowIndex=0;  //The index of the current gas station
		double nowDis=0;
		double nowCapacity=capacity;
		bool bNotArrived=false;

		while(nowIndex<nStation){

			//Find the specific gas station
			double tmpMinPrice=INF;
			int tmpMinIndex=nowIndex;
			double tmpMaxDis=vecStation[nowIndex].distance+capacity*avgDis;

			for(int i=nowIndex+1;i<=nStation&&vecStation[i].distance<=tmpMaxDis;i++){
				if(vecStation[nowIndex].price>vecStation[i].price){
					tmpMinPrice=vecStation[i].price;
					tmpMinIndex=i;
					break;
				}
				if(tmpMinPrice>=vecStation[i].price){
					tmpMinPrice=vecStation[i].price;
					tmpMinIndex=i;
				}
			}

			//Can't reach the destination
			if(tmpMinPrice==INF){
				bNotArrived=true;
				break;
			}

			if(tmpMinPrice>=vecStation[nowIndex].price){

				minPrice+=nowCapacity*vecStation[nowIndex].price;
				nowCapacity=0;


			}else{
				//Consider whether the rest oil can support us reach the next station
				double tmpDis=(capacity-nowCapacity)*avgDis;
				if(tmpDis<vecStation[tmpMinIndex].distance-vecStation[nowIndex].distance){
					double tmpCapacity=(vecStation[tmpMinIndex].distance-vecStation[nowIndex].distance-tmpDis)/avgDis;
					minPrice+=tmpCapacity*vecStation[nowIndex].price;
					nowCapacity-=tmpCapacity;
				}
			}

			nowCapacity+=(vecStation[tmpMinIndex].distance-vecStation[nowIndex].distance)/avgDis;
			nowIndex=tmpMinIndex;
			maxDis=capacity*avgDis+vecStation[nowIndex].distance;

		}
		if(bNotArrived){
			printf("The maximum travel distance = %.2f\n",maxDis);
		}else{
			printf("%.2f\n",minPrice);
		}

	}
	return 0;
}

Repair the Wall

题目描述
Long time ago , Kitty lived in a small village. The air was fresh and the scenery was very beautiful. The only thing that troubled her is the typhoon.
When the typhoon came, everything is terrible. It kept blowing and raining for a long time. And what made the situation worse was that all of Kitty’s walls were made of wood.
One day, Kitty found that there was a crack in the wall. The shape of the crack is
a rectangle with the size of 1×L (in inch). Luckly Kitty got N blocks and a saw(锯子) from her neighbors.
The shape of the blocks were rectangle too, and the width of all blocks were 1 inch. So, with the help of saw, Kitty could cut down some of the blocks(of course she could use it directly without cutting) and put them in the crack, and the wall may be repaired perfectly, without any gap.
Now, Kitty knew the size of each blocks, and wanted to use as fewer as possible of the blocks to repair the wall, could you help her ?
输入
The problem contains many test cases, please process to the end of file( EOF ).
Each test case contains two lines.
In the first line, there are two integers L(0<L<1000000000) and N(0<=N<600) which
mentioned above.
In the second line, there are N positive integers. The ith integer Ai(0<Ai<1000000000 ) means that the ith block has the size of 1×Ai (in inch).
输出
For each test case , print an integer which represents the minimal number of blocks are needed.
If Kitty could not repair the wall, just print “impossible” instead.
样例输入
2 2
12 11
14 3
27 11 4
109 5
38 15 6 21 32
5 3
1 1 1
样例输出
1
1
5
impossible
程序

#include<iostream>
#include<algorithm>
#include<vector>
#include<functional>
using namespace std;
int L,N;
vector<int> vec;
int main(){
	while(cin>>L>>N){
		vec.resize(N);
		for(int i=0;i<N;i++){
			cin>>vec[i];
		}
		sort(vec.begin(),vec.end(),greater<int>());
		int tmpL=0;
		int nCount=0;
		int index=0;
		while(tmpL<L&&nCount<vec.size()){
			tmpL+=vec[nCount++];
		}
		if(tmpL<L){
			cout<<"impossible"<<endl;
		}else{
			cout<<nCount<<endl;
		}
	}
	return 0;
}

FatMouse’s Trade

题目描述
FatMouse prepared M pounds of cat food, ready to trade with the cats guarding the warehouse containing his favorite food, JavaBean.
The warehouse has N rooms. The i-th room contains J[i] pounds of JavaBeans and requires F[i] pounds of cat food. FatMouse does not have to trade for all the JavaBeans in the room, instead, he may get J[i]* a% pounds of JavaBeans if he pays F[i]* a% pounds of cat food. Here a is a real number. Now he is assigning this homework to you: tell him the maximum amount of JavaBeans he can obtain.
输入
The input consists of multiple test cases. Each test case begins with a line containing two non-negative integers M and N. Then N lines follow, each contains two non-negative integers J[i] and F[i] respectively. The last test case is followed by two -1’s. All integers are not greater than 1000.
输出
For each test case, print in a single line a real number accurate up to 3 decimal places, which is the maximum amount of JavaBeans that FatMouse can obtain.
样例输入
4 2
4 7
1 3
5 5
4 8
3 8
1 2
2 5
2 4
-1 -1
样例输出
2.286
2.500
程序

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;

struct Room{
	int javaBean;
	int food;
	double ratio;
	Room(){}
	Room(int JavaBean, int Food, double Ratio)
	:javaBean(JavaBean),food(Food),ratio(Ratio){}
	bool operator < (const Room tmp) const{
		return ratio>tmp.ratio;
	}
};

int M,N;
vector<Room> vec;

int main(){
	while(cin>>M>>N&&(M!=-1||N!=-1)){
		vec.clear();
		for(int i=0;i<N;i++){
			int j,f;
			cin>>j>>f;
			vec.push_back(Room(j,f,(double)j/f));
		}
		sort(vec.begin(),vec.end());
		int index=0;
		double result=0;
		while(M!=0){
			if(M>=vec[index].food){
				M-=vec[index].food;
				result+=vec[index].javaBean;
			}else{
				result+=vec[index].ratio*M;
				M=0;
			}
			index++;
		}
		printf("%.3f\n",result);
	}
	return 0;
}

迷瘴

题目描述
小明正在玩游戏，他控制的角色正面临着幽谷的考验——
幽谷周围瘴气弥漫，静的可怕，隐约可见地上堆满了骷髅。由于此处长年不见天日，导致空气中布满了毒素，一旦吸入体内，便会全身溃烂而死。
幸好小明早有防备，提前备好了解药材料（各种浓度的万能药水）。现在只需按照配置成不同比例的浓度。
现已知小明随身携带有n种浓度的万能药水，体积V都相同，浓度则分别为Pi%。并且知道，针对当时幽谷的瘴气情况，只需选择部分或者全部的万能药水，然后配置出浓度不大于 W%的药水即可解毒。
现在的问题是：如何配置此药，能得到最大体积的当前可用的解药呢？
特别说明：由于幽谷内设备的限制,只允许把一种已有的药全部混入另一种之中（即：不能出现对一种药只取它的一部分这样的操作）。
输入
输入数据的第一行是一个整数C，表示测试数据的组数；
每组测试数据包含2行，首先一行给出三个正整数n,V,W(1<=n,V,W<=100)；
接着一行是n个整数，表示n种药水的浓度Pi%(1<=Pi<=100)。
输出
对于每组测试数据，请输出一个整数和一个浮点数；
其中整数表示解药的最大体积，浮点数表示解药的浓度(四舍五入保留2位小数)；
如果不能配出满足要求的的解药，则请输出0 0.00。
样例输入
2
1 35 68
1
2 79 25
59 63
样例输出
35 0.01
0 0.00
程序

#include<iostream>
#include<algorithm>
#include<functional>
#include<vector>
using namespace std;

int N,V,M;
vector<int> vec;

int main(){
	int C;
	cin>>C;
	while(C--){
		cin>>N>>V>>M;
		vec.resize(N);
		for(int i=0;i<N;i++) cin>>vec[i];
		sort(vec.begin(),vec.end(),less<int>());
		double drog=0;
		int maxV=0;
		double ratio=0;
		int index=0;
		while((index==0||(drog/(index*V)<=M/100.0))&&index<N){
			drog+=vec[index]/100.0*V;
			index++;
			if(drog/(index*V)<=M/100.0){
				maxV+=V;
				ratio=drog/(index*V);
			}
		}
		printf("%d %0.2f\n",maxV,ratio);
	}
	return 0;
}

找零钱

题目描述
小智去超市买东西，买了不超过一百块的东西。收银员想尽量用少的纸币来找钱。
纸币面额分为50 20 10 5 1 五种。请在知道要找多少钱n给小明的情况下，输出纸币数量最少的方案。 1<=n<=99;
输入
有多组数据 1<=n<=99;
输出
对于每种数量不为0的纸币，输出他们的面值*数量，再加起来输出
样例输入
25
32
样例输出
20*1+5*1
20*1+10*1+1*2
程序

#include<iostream>
#include<algorithm>
using namespace std;
int money[2][5]={
	50,20,10,5,1,
	0,0,0,0,0
};

int main(){
	int n;
	while(cin>>n){
		for(int i=0;i<5;i++){
			money[1][i]=0;
		}
		for(int i=0;i<5;i++){
			while(n>=money[0][i]){
				n-=money[0][i];
				money[1][i]++;
			}
			if(n==0) break;
		}
		bool bFirst=true;
		for(int i=0;i<5;i++){

			if(money[1][i]!=0){
				if(!bFirst) cout<<"+";
				bFirst=false;
				cout<<money[0][i]<<"*"<<money[1][i];
			}
		}
		cout<<endl;
	}
	return 0;
}

二分法

技巧：

1、矩阵每行升序，每列升序，从左下角或右上角开始二分！
2、求两个数组的和，满足每一个关系，可以先排序，再从i=0…m,j=n-1…0，双指针开始二分！时间复杂度降维$O(n\log{n}+n), n=max(m,n)$

找x

题目描述
输入一个数n，然后输入n个数值各不相同，再输入一个值x，输出这个值在这个数组中的下标（从0开始，若不在数组中则输出-1）。
输入
测试数据有多组，输入n(1<=n<=200)，接着输入n个数，然后输入x。
输出
对于每组输入,请输出结果。
样例输入
4
1 2 3 4
3
样例输出
2
程序

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;

struct Node{
	int index;
	int data;
	Node(){}
	Node(int Index,int Data):index(Index),data(Data){}
	bool operator < (const Node &tmp) const{
		return data<tmp.data;
	}
};
vector<Node> vec;
int n;
int findIndexOfx(int x){

	int left=0,right=n-1;

	while(left<=right){
		int mid=left+(right-left)/2;
		if(vec[mid].data==x) return vec[mid].index;
		else if(vec[mid].data>x) right=mid-1;
		else left=mid+1;
	}
	return -1;
}
int main(){
	while(cin>>n){
		vec.resize(n);
		for(int i=0;i<n;i++){
			cin>>vec[i].data;
			vec[i].index=i;
		}
		sort(vec.begin(),vec.end());
		int x;
		cin>>x;
		cout<<findIndexOfx(x)<<endl;
	}
	return 0;
}

打印极值点坐标

描述
在一个整数数组上，对于下标为i的整数，如果它大于所有它相邻的整数，或者小于所有它相邻的整数，则称为该整数为一个极值点，极值点的下标就是i。
输入
有2×n+1行输入：第一行是要处理的数组的个数n；对其余2×n行，第一行是此数组的元素个数k(4<k<80)，第二行是k个整数，每两个整数之间用空格分隔。
输出
输出为n行：每行对应于相应数组的所有极值点下标值，下标值之间用空格分隔。
样例输入
3
10
10 12 12 11 11 12 23 24 12 12
15
12 12 122 112 222 211 222 221 76 36 31 234 256 76 76
15
12 14 122 112 222 222 222 221 76 36 31 234 256 76 73
样例输出
0 7
2 3 4 5 6 10 12
0 2 3 10 12 14
程序

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;

int nCase;
vector<int> vec;
int main(){
	cin>>nCase;
	while(nCase--){
		int nCount;
		cin>>nCount;
		vec.resize(nCount);
		for(int i=0;i<nCount;i++) cin>>vec[i];

		bool bFirst=true;
		if(vec[0]!=vec[1]) {
			cout<<0;
			bFirst=false;
		}
		for(int i=1;i<nCount-1;i++){
			if((vec[i]>vec[i+1]&&vec[i]>vec[i-1])
				||(vec[i]<vec[i+1]&&vec[i]<vec[i-1])){
				if(bFirst) bFirst=false;
				else cout<<" ";
				cout<<i;
			}
		}
		if(vec[nCount-1]!=vec[nCount-2]){
			if(bFirst) bFirst=false;
			else cout<<" ";
			cout<<nCount-1;
		}
		cout<<endl;
	}
	return 0;
}

查找

题目描述
输入数组长度 n
输入数组 a[1…n]
输入查找个数m
输入查找数字b[1…m]
输出 YES or NO 查找有则YES 否则NO 。
输入
输入有多组数据。
每组输入n，然后输入n个整数，再输入m，然后再输入m个整数（1<=m<=n<=100）。
输出
如果在n个数组中输出YES否则输出NO。
样例输入
6
3 2 5 4 7 8
2
3 6
样例输出
YES
NO
程序

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;

vector<int> vec;
int nCount;

bool findX(int x){
	int left=0,right=nCount-1;
	while(left<=right){
		int mid=left+(right-left)/2;
		if(vec[mid]==x) return true;
		else if(vec[mid]>x) right=mid-1;
		else left=mid+1;
	}
	return false;
}
int main(){
	while(cin>>nCount){
		vec.resize(nCount);
		for(int i=0;i<nCount;i++){
			cin>>vec[i];
		}
		sort(vec.begin(),vec.end());
		int nFind;
		cin>>nFind;
		for(int i=0;i<nFind;i++){
			int x;
			cin>>x;
			if(findX(x)){
				cout<<"YES"<<endl;
			}else{
				cout<<"NO"<<endl;
			}
		}
	}
	return 0;
}

Two Pointers

二路归并排序(mergesort)递归法 [2*+]

题目描述
二路归并排序(mergesort)递归法
用递归法进行二路归并排序
输入
第一行一个数据n，表示有n个数要排序。接下来n行每行一个<=10^7的整数。
输出
n行，由小到大排序后的数据
数据规模：n<=10^5
思考：两个递归都会被执行吗？
程序

#include<iostream>
#include<vector>
using namespace std;
/*
Warning: server error
Runtime error 20%
*/
typedef int Status;
const int OK=1;
const int ERROR=0;

Status merge(vector<int> &vec,int L1,int R1,int L2,int R2){
	int index=0;
	int start=L1;
	vector<int> temp;
	temp.resize(R2-L1+1);
	while(L1<=R1&&L2<=R2){
		if(vec[L1]<=vec[L2]) temp[index++]=vec[L1++];
		else temp[index++]=vec[L2++];
	}
	while(L1<=R1) temp[index++]=vec[L1++];
	while(L2<=R2) temp[index++]=vec[L2++];
	for(int i=0;i<temp.size();i++){
		vec[start++]=temp[i];
	}
	return OK;
}
Status mergeSort(vector<int> &vec,int left,int right){
	if(left<right){
		int mid=left+(right-left)/2;
		mergeSort(vec,left,mid);
		mergeSort(vec,mid+1,right);
		merge(vec,left,mid,mid+1,right);
	}
	return OK;
}
int main(){
	int n;
	vector<int> vec;

	while(cin>>n){
		vec.resize(n);
		for(int i=0;i<n;i++){
			cin>>vec[i];
		}
		mergeSort(vec,0,n-1);
		vector<int>::iterator it=vec.begin();
		while(it!=vec.end()){
			cout<<*it<<endl;
			it++;
		}
	}
	return 0;
}

基础排序III：归并排序

题目描述
归并排序是一个时间复杂度为O(nlogn)的算法，对于大量数据远远优于冒泡排序与插入排序。
这是一道排序练习题，数据量较大，请使用归并排序完成。
输入
第一行一个数字n，代表输入的组数
其后每组第一行输入一个数字m，代表待排序数字的个数
其后m行每行一个数据，大小在1～100000之间，互不相等，最多有10万个数据。
输出
升序输出排好序的数据，每行一个数字
样例输入
1
10
10
9
8
7
6
5
4
3
2
1
样例输出
1
2
3
4
5
6
7
8
9
10
程序

#include<iostream>
#include<vector>
using namespace std;
typedef int Status;
const int OK=1;
const int ERROR=0;

Status merge(vector<int> &vec,int L1,int R1,int L2,int R2){
	int index=0;
	int start=L1;
	vector<int> temp;
	temp.resize(R2-L1+1);
	while(L1<=R1&&L2<=R2){
		if(vec[L1]<=vec[L2]) temp[index++]=vec[L1++];
		else temp[index++]=vec[L2++];
	}
	while(L1<=R1) temp[index++]=vec[L1++];
	while(L2<=R2) temp[index++]=vec[L2++];
	for(int i=0;i<temp.size();i++){
		vec[start++]=temp[i];
	}
	return OK;
}
Status mergeSort(vector<int> &vec,int left,int right){
	if(left<right){
		int mid=left+(right-left)/2;
		mergeSort(vec,left,mid);
		mergeSort(vec,mid+1,right);
		merge(vec,left,mid,mid+1,right);
	}
	return OK;
}
int main(){
	int nCase;
	vector<int> vec;
 	cin>>nCase;
	while(nCase--){
		int n;
		cin>>n;
		vec.resize(n);
		for(int i=0;i<n;i++){
			cin>>vec[i];
		}
		mergeSort(vec,0,n-1);
		vector<int>::iterator it=vec.begin();
		while(it!=vec.end()){
			cout<<*it<<endl;
			it++;
		}
	}
	return 0;
}

快速排序 qsort [2*]

题目描述
输入n个整数，用快速排序的方法进行排序
Input
第一行数字n 代表接下来有n个整数
接下来n行，每行一个整数
Output
升序输出排序结果
每行一个数据
Sample Input
5
12
18
14
13
16
Sample Output
12
13
14
16
18
Procedure

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
typedef int Status;
const int OK=1;
const int ERROR=0;

int partition(vector<int> &vec,int left,int right){
	int temp=vec[left];
	while(left<right){
		while(left<right&&vec[right]>=temp) right--;
		vec[left]=vec[right];
		while(left<right&&vec[left]<=temp) left++;
		vec[right]=vec[left];
	}
	vec[left]=temp;
	return left;
}

Status quickSort(vector<int> &vec,int left,int right){
	if(left<right){
		int pos=partition(vec,left,right);
		quickSort(vec,left,pos-1);
		quickSort(vec,pos+1,right);
	}
	return OK;
}

int main(){
	int n;
	vector<int> vec;
	while(cin>>n){
		vec.resize(n);
		for(int i=0;i<n;i++) cin>>vec[i];
		quickSort(vec,0,n-1);
		for(vector<int>::iterator it=vec.begin();it!=vec.end();it++){
			cout<<*it<<endl;
		}
	}
	return 0;
}

二分递归快排（Qsort） [2*]

题目描述
二分递归快排（Qsort）
用二分递归的方法实现快排
输入
第一行一个数据n，表示有n个数要排序。接下来n行每行一个<=10^7的整数。
输出
n行，由小到大排序后的数据
数据规模：n<=10^5
思考：两个递归都会被执行吗？有几种可能？
程序

#include<iostream>
#include<algorithm>
#include<vector>
#include<ctime>
using namespace std;
typedef int Status;
const int OK=1;
const int ERROR=0;

int partition(vector<int> &vec,int left,int right){
	int index=left+rand()%(right-left+1);
	int temp=vec[index];
	swap(vec[index],vec[left]);
	while(left<right){
		while(left<right&&vec[right]>=temp) right--;
		vec[left]=vec[right];
		while(left<right&&vec[left]<=temp) left++;
		vec[right]=vec[left];
	}
	vec[left]=temp;
	return left;
}

Status quickSort(vector<int> &vec,int left,int right){
	if(left<right){
		int pos=partition(vec,left,right);
		quickSort(vec,left,pos-1);
		quickSort(vec,pos+1,right);
	}
	return OK;
}

int main(){
	srand((unsigned)time(NULL));
	int n;
	vector<int> vec;
	while(cin>>n){
		vec.resize(n);
		for(int i=0;i<n;i++) cin>>vec[i];
		quickSort(vec,0,n-1);
		for(vector<int>::iterator it=vec.begin();it!=vec.end();it++){
			cout<<*it<<endl;
		}
	}
	return 0;
}

其他高效技巧与算法

求第k大的数

给定一个长度为n（1≤n≤1,000,000）的无序正整数序列，以及另一个数k（1≤k≤1,000,000）（关于第k大的数：例如序列{1,2,3,4,5,6}中第3大的数是4。）
输入
第一行两个正整数m,n。
第二行为n个正整数。
输出
第k大的数。
样例输入
6 3
1 2 3 4 5 6
样例输出
4
程序

#include<iostream>
#include<algorithm>
#include<vector>
#include<ctime>
using namespace std;
typedef int Status;
const int OK=1;
const int ERROR=0;
int partition(vector<int> &vec,int left,int right){
	int index=rand()%(right-left+1)+left;
	int temp=vec[index];
	swap(vec[index],vec[left]);
	while(left<right){
		while(left<right&&vec[right]>=temp) right--;
		vec[left]=vec[right];
		while(left<right&&vec[left]<=temp) left++;
		vec[right]=vec[left];
	}
	vec[left]=temp;
	return left;
}

int randSelect(vector<int> &vec,int left,int right,int k){
	int len=vec.size();
	int pos=partition(vec,left,right);
	while(pos+k!=len){
		if(pos<len-k){
			pos=partition(vec,pos+1,right);
		}else{
			pos=partition(vec,left,pos-1);
		}
	}
	return vec[pos];
}
int main(){
	srand((unsigned)time(NULL));
	int n,k;
	vector<int> vec;
	while(cin>>n>>k){
		vec.resize(n);
		for(int i=0;i<n;i++){
			cin>>vec[i];
		}
		cout<<randSelect(vec,0,n-1,k)<<endl;
	}
	return 0;
}

简单数学

守形数

题目描述
守形数是这样一种整数，它的平方的低位部分等于它本身。
比如25的平方是625，低位部分是25，因此25是一个守形数。
编一个程序，判断N是否为守形数。

输入
输入包括1个整数N，2<=N<100。

输出
可能有多组测试数据，对于每组数据，
输出”Yes!”表示N是守形数。
输出”No!”表示N不是守形数。

样例输入
6
11
样例输出
Yes!
No!
程序

#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;

bool judge(string str){
	int n=0;
	for(int i=0;i<str.length();i++){
		n=n*10+str[i]-'0';
	}
	n*=n;
	vector<char> vec;
	int count=0;
	while(n!=0&&count!=str.length()){
		int tmp=n%10;
		vec.push_back(tmp+'0');
		n/=10;
		count++;
	}
	reverse(vec.begin(),vec.end());

	if(vec.size()!=str.length()) return false;
	else{
		for(int i=0;i<str.length();i++){
			if(vec[i]!=str[i]) return false;
		}
		return true;
	}
}
int main(){
	string str;
	while(cin>>str){

		if(judge(str)) cout<<"Yes!"<<endl;
		else cout<<"No!"<<endl;
	}
	return 0;
}

反序数

题目描述
设N是一个四位数，它的9倍恰好是其反序数（例如：1234的反序数是4321）
求N的值
输入
程序无任何输入数据。
输出
输出题目要求的四位数，如果结果有多组，则每组结果之间以回车隔开。
程序

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

vector<int> transform(int x){
	vector<int> vec;
	while(x!=0){
		int tmp=x%10;
		vec.push_back(tmp);
		x/=10;
	}
	return vec;
}
bool judge(vector<int> vecOne,vector<int> vecTwo){
	if(vecOne.size()!=vecTwo.size()) return false;

	for(int i=0;i<vecOne.size();i++){
		if(vecOne[i]!=vecTwo[i]) return false;
	}
	return true;
}

int main(){
	transform(1000);
	bool bFirst=true;
	for(int i=1000;i<10000;i++){
		vector<int> vecOne=transform(i);
		reverse(vecOne.begin(),vecOne.end());

		vector<int> vecTwo=transform(i*9);
		if(judge(vecOne,vecTwo)){
			if(bFirst){
				bFirst=false;
			}else{
				cout<<",";
			}
			cout<<i;
		}
	}
	cout<<endl;
	return 0;
}

百鸡问题

题目描述
用小于等于n元去买100只鸡，大鸡5元/只，小鸡3元/只,还有1/3元每只的一种小鸡，分别记为x只,y只,z只。编程求解x,y,z所有可能解。
输入
测试数据有多组，输入n。
输出
对于每组输入,请输出x,y,z所有可行解，按照x，y，z依次增大的顺序输出。
样例输入
45
样例输出
x=0,y=0,z=100
x=0,y=1,z=99
x=0,y=2,z=98
x=0,y=3,z=97
x=0,y=4,z=96
x=1,y=0,z=99
x=1,y=1,z=98
x=1,y=2,z=97
x=2,y=0,z=98
程序

#include<iostream>
using namespace std;

void calculate(int n){
	for(int i=0;i<=100;i++){
		for(int j=0;j<=100-i;j++){
			double cost=i*5+j*3+1/3.0*(100-i-j);
			if(cost<=n){
				cout<<"x="<<i<<",y="<<j<<",z="<<100-i-j<<endl;
			}
		}
	}
}
int main(){
	int n;
	while(cin>>n){
		calculate(n);
	}
	return 0;
}

abc

题目描述
设a、b、c均是0到9之间的数字，abc、bcc是两个三位数，且有：abc+bcc=532。求满足条件的所有a、b、c的值。
输入
题目没有任何输入。
输出
请输出所有满足题目条件的a、b、c的值。
a、b、c之间用空格隔开。
每个输出占一行。
程序

#include<iostream>
using namespace std;

int main(){
	for(int a=1;a<10;a++){
		for(int b=1;b<10;b++){
			for(int c=0;c<10;c++){
				int abc=a*100+b*10+c;
				int bcc=b*100+c*10+c;
				if(abc+bcc==532) cout<<a<<" "<<b<<" "<<c<<endl;
			}
		}
	}
	return 0;
}

众数

题目描述
输入20个数，每个数都在1-10之间，求1-10中的众数（众数就是出现次数最多的数，如果存在一样多次数的众数，则输出权值较小的那一个）。
输入
测试数据有多组，每组输入20个1-10之间的数。
输出
对于每组输入,请输出1-10中的众数。
注意如果存在一样多次数的众数，则输出权值较小的那一个。
样例输入
8 9 6 4 6 3 10 4 7 4 2 9 1 6 5 6 2 2 3 8
样例输出
6
程序

#include<iostream>
#include<algorithm>
using namespace std;

int Hash[11];

int main(){
	int tmp;
	while(cin>>tmp){
		fill(Hash,Hash+11,0);
		Hash[tmp]++;
		for(int i=2;i<=20;i++){
			cin>>tmp;
			Hash[tmp]++;
		}
		int max=0;
		int maxIndex=0;
		for(int i=1;i<=10;i++){
			if(Hash[i]>max){
				max=Hash[i];
				maxIndex=i;
			}
		}
		cout<<maxIndex<<endl;
	}
	return 0;
}

整数和

题目描述
编写程序，读入一个整数N。若N为非负数，则计算N 到2N 之间的整数和；若N为一个负数，则求2N 到N 之间的整数和。
输入
第一行表示样例数m，接下来m行每行一个整数N，N的绝对值不超过100。
输出
输出m行，每行表示对应的题目所求。
样例输入
2
2
-1
样例输出
9
-3
程序

#include<iostream>
using namespace std;

int main(){
	int m;
	cin>>m;
	while(m--){
		int n;
		cin>>n;
		int a,b;
		if(n>=0){
			a=n;
			b=2*n;
		}else{
			a=2*n;
			b=n;
		}
		int sum=0;
		for(int i=a;i<=b;i++){
			sum+=i;
		}
		cout<<sum<<endl;
	}

	return 0;
}

多项式的值

题目描述
实现一个多项式的类（a+bx+cx^2+dx^3+…+），要求输入该多项式的系数和x
的值后打印出这个多项式的值。
*输入**
输入第一行为样例数m，对于每个样例，第一行为多项式最高项次数n，接下来n+1个整数表示每项系数，最后一个整数x，n不超过10。
输出
输出m行，表示个多项式代入x后的值。
样例输入
1
2
1 2 3
2
样例输出
17
程序

#include<iostream>
#include<vector>
#include<cmath>
using namespace std;

vector<int> vec;
int x;
int n;
int m;
int main(){
	cin>>m;
	while(m--){
		cin>>n;
		vec.resize(n+1);
		for(int i=0;i<n+1;i++) cin>>vec[i];
		cin>>x;
		int value=0;
		for(int i=0;i<n+1;i++){
			value+=vec[i]*(int)pow(x,i);
		}
		cout<<value<<endl;
	}
	return 0;
}

迭代求立方根

题目描述
立方根的逼近迭代方程是 y(n+1) = y(n)2/3 + x/(3y(n)y(n)),其中y0=x.求给定的x经过n次迭代后立方根的值。
*输入**
输入有多组数据。
每组一行，输入x n。
输出
迭代n次后的立方根，double精度,保留小数点后面六位。
样例输入
4654684 1
65461 23
样例输出
3103122.666667
40.302088
程序

#include<iostream>
using namespace std;

int main(){
	double x;
	int n;
	while(cin>>x>>n){
		double y[n+1];
		y[0]=x;
		for(int i=0;i<n;i++){
			y[i+1]=y[i]*2/3.0+x/(3*y[i]*y[i]);
		}
		printf("%.6f\n",y[n]);
	}
	return 0;
}

与7无关的数

题目描述
一个正整数,如果它能被7整除,或者它的十进制表示法中某个位数上的数字为7,
则称其为与7相关的数.现求所有小于等于n(n<100)的与7无关的正整数的平方和。
输入
案例可能有多组。对于每个测试案例输入为一行,正整数n,(n<100)
输出
对于每个测试案例输出一行，输出小于等于n的与7无关的正整数的平方和。
样例输入
6
12
18
样例输出
91
601
1575
程序

#include<iostream>
#include<cmath>
#include<vector>
using namespace std;

bool isRelative(int x){
	if(x%7==0) return true;
	if(x%10==7) return true;
	x/=10;
	if(x==7)return true;
	return false;
}
int main(){
	int n;
	vector<int> vec;
	while(cin>>n){
		vec.clear();
		for(int i=1;i<=n;i++){
			if(!isRelative(i)){
				vec.push_back(i);
			}
		}
		int sum=0;
		for(int i=0;i<vec.size();i++){
			sum+=(int)pow(vec[i],2);
		}
		cout<<sum<<endl;
	}
	return 0;
}

鸡兔同笼

题目描述
一个笼子里面关了鸡和兔子（鸡有2只脚，兔子有4只脚，没有例外）。已经知道了笼子里面脚的总数a，问笼子里面至少有多少只动物，至多有多少只动物。
输入
第1行是测试数据的组数n，后面跟着n行输入。每组测试数据占1行，每行一个正整数a (a < 32768)
输出
输出包含n行，每行对应一个输入,包含两个正整数，第一个是最少的动物数，第二个是最多的动物数，两个正整数用一个空格分开
如果没有满足要求的答案，则输出两个0。
样例输入
2
18
5
样例输出
5 9
0 0
程序

#include<iostream>
using namespace std;

int main(){
	int n;
	cin>>n;
	while(n--){
		int x;
		cin>>x;
		int min=0,max=0;
		if(x&1!=0) {
			printf("%d %d\n",0,0);
			continue;
		}
		int tmp=x;
		while(tmp>=4){
			tmp-=4;
			min++;
		}
		if(tmp>0) min++;
		tmp=x;
		while(tmp>=2){
			tmp-=2;
			max++;
		}
		cout<<min<<" "<<max<<endl;
	}
	return 0;
}

最大公因数与最小公倍数

Least Common multiple

Description
The least common multiple (LCM) of a set of positive integers is the smallest positive integer which is divisible by all the numbers in the set. For example, the LCM of 5, 7 and 15 is 105.

Input
Input will consist of multiple problem instances. The first line of the input will contain a single integer indicating the number of problem instances. Each instance will consist of a single line of the form m n1 n2 n3 … nm where m is the number of integers in the set and n1 … nm are the integers. All integers will be positive and lie within the range of a 32-bit integer.

Output
For each problem instance, output a single line containing the corresponding LCM. All results will lie in the range of a 32-bit integer.

Sample Input
2
2 3 5
3 4 6 12
Sample Output
15
12
Procedure

#include<iostream>
#include<vector>
using namespace std;

vector<long> vec;

long gcd(int x,int y){
	if(y==0) return x;
	else return gcd(y,x%y);
}
int main(){
	int n;
	cin>>n;
	while(n--){

		int m;
		cin>>m;
		vec.resize(m);
		long result=0;
		for(int i=0;i<m;i++){
			cin>>vec[i];
			if(i==0){
				result=vec[i];
			}
			else{
				result=result*vec[i]/gcd(result,vec[i]);
			}
		}
		cout<<result<<endl;
	}
	return 0;
}

分数的四则运算

模板

#include<iostream>
#include<cmath>
using namespace std;

struct Fraction{
	int up;    //Numerator
	int down;  //Denominator
  Fraction(){} //Default Constructor
	Fraction(int Up,int Down):up(Up),down(Down){} //
};

//Return the least common mutiple of x and y
int gcd(int x,int y){
	return !y? x:gcd(y,x%y);
}

//Reduce the fraction
//1.Denominator is non-negative: if the fraction is negative, just make the numerator negative
//2.if the fraction is zero, just up=0, down=1
//3.The greatest common divisor of numerator and denominator must be '1'.
Fraction reduction(Fraction fraction){
	if(fraction.down<0){
		fraction.up=-fraction.up;
		fraction.down=-fraction.down;
	}
	if(fraction.up==0){
		fraction.down=1;
	}else{
		int gcd=d(abs(fraction.up),abs(fraction.down));
		fraction.up/=d;
		fraction.down/=d;
	}
	return fraction;
}

//Addition
Fraction addition(Fraction f1,Fraction f2){
	Fraction fraction;
	fraction.up=f1.up*f2.down+f2.up*f1.down;
	fraction.down=f1.down*f2.down;
	return reduction(fraction);
}

//Subtraction
Fraction subtraction(Fraction f1,Fraction f2){
	Fraction fraction;
	fraction.up=f1.up*f2.down-f2.up*f1.down;
	fraction.down=f1.down*f2.down;
	return reduction(fraction);
}

//Multiplication
Fraction multiplication(Fraction f1,Fraction f2){
	Fraction fraction;
	fraction.up=f1.up*f2.up;
	fraction.down=f1.down*f2.down;
	return reduction(fraction);
}

//Division
Fraction division(Fraction f1,Fraction f2){
	Fraction fraction;
	fraction.up=f1.up*f2.down;
	fraction.down=f1.down*f2.up;
	return reduction(fraction);
}

分数矩阵

题目描述
我们定义如下矩阵：
1/1 1/2 1/3
1/2 1/1 1/2
1/3 1/2 1/1
矩阵对角线上的元素始终是1/1，对角线两边分数的分母逐个递增。
请求出这个矩阵的总和。
输入
输入包含多组测试数据。每行给定整数N（N<50000），表示矩阵为NN。当N=0时，输入结束。
*输出**
输出答案，结果保留2位小数。
样例输入
1
2
3
4
0
样例输出
1.00
3.00
5.67
8.83
程序

#include<iostream>
#include<cmath>
using namespace std;

int main(){
	int n;
	while(cin>>n&&n!=0){
		double result=0;
		for(int i=0;i<n;i++){
			double tmp=(n-i)*1.0/(i+1);
			if(i!=0) tmp*=2;
			result+=tmp;
		}
		printf("%.2f\n",result);
	}
	return 0;
}

1062. 最简分数(20)

一个分数一般写成两个整数相除的形式：N/M，其中M不为0。最简分数是指分子和分母没有公约数的分数表示形式。
现给定两个不相等的正分数 N1/M1 和 N2/M2，要求你按从小到大的顺序列出它们之间分母为K的最简分数。
输入格式
输入在一行中按N/M的格式给出两个正分数，随后是一个正整数分母K，其间以空格分隔。题目保证给出的所有整数都不超过1000。
输出格式
在一行中按N/M的格式列出两个给定分数之间分母为K的所有最简分数，按从小到大的顺序，其间以1个空格分隔。行首尾不得有多余空格。题目保证至少有1个输出。
输入样例
7/18 13/20 12
输出样例
5/12 7/12
程序

#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;

struct Fraction{
	int up;    //Numerator
	int down;  //Denominator
  Fraction(){} //Default Constructor
	Fraction(int Up,int Down):up(Up),down(Down){} //
};

//Return the least common mutiple of x and y
int gcd(int x,int y){
	return !y? x:gcd(y,x%y);
}

//Reduce the fraction
//1.Denominator is non-negative: if the fraction is negative, just make the numerator negative
//2.if the fraction is zero, just up=0, down=1
//3.The greatest common divisor of numerator and denominator must be '1'.
Fraction reduction(Fraction fraction){
	if(fraction.down<0){
		fraction.up=-fraction.up;
		fraction.down=-fraction.down;
	}
	if(fraction.up==0){
		fraction.down=1;
	}else{
		int d=gcd(abs(fraction.up),abs(fraction.down));
		fraction.up/=d;
		fraction.down/=d;
	}
	return fraction;
}

//Addition
Fraction addition(Fraction f1,Fraction f2){
	Fraction fraction;
	fraction.up=f1.up*f2.down+f2.up*f1.down;
	fraction.down=f1.down*f2.down;
	return reduction(fraction);
}

//Subtraction
Fraction subtraction(Fraction f1,Fraction f2){
	Fraction fraction;
	fraction.up=f1.up*f2.down-f2.up*f1.down;
	fraction.down=f1.down*f2.down;
	return reduction(fraction);
}

//Multiplication
Fraction multiplication(Fraction f1,Fraction f2){
	Fraction fraction;
	fraction.up=f1.up*f2.up;
	fraction.down=f1.down*f2.down;
	return reduction(fraction);
}

//Division
Fraction division(Fraction f1,Fraction f2){
	Fraction fraction;
	fraction.up=f1.up*f2.down;
	fraction.down=f1.down*f2.up;
	return reduction(fraction);
}

//f1<f2
bool cmp(Fraction f1,Fraction f2){
	int d=gcd(f1.down,f2.down);
	int lcm=f1.down*f2.down/d;
	f1.up*=lcm/f1.down;
	f2.up*=lcm/f2.down;
	if(f1.up<f2.up) return true;
	else return false;
}
int main(){
	Fraction f1,f2;
	int k;
	while(scanf("%d/%d %d/%d %d",&f1.up,&f1.down,&f2.up,&f2.down,&k)!=EOF){
		if(!cmp(f1,f2)) swap(f1,f2);
		bool bFirst=true;
		for(int i=1;i<k;i++){
			Fraction fraction(i,k);
			if(cmp(f1,fraction)&&cmp(fraction,f2)){
				fraction=reduction(fraction);
				if(fraction.down==k){
					if(bFirst){
						bFirst=false;
					}else{
						printf(" ");
					}
					printf("%d/%d",fraction.up,fraction.down);
				}
			}
		}
		printf("\n");
	}
	return 0;
}

素数

模板

#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
//Judge whether the x is a prime number
bool isPrime(int x){
	if(x<=1) return false;
	for(int i=2;i*i<=x;i++){
		if(x%i==0) return false;
	}
	return true;
}//O(sprt(n))

//Record all prime numbers between 1 to x

//Eratosthenes
const int MAXN=101;
int prime[MAXN];
bool bMarked[MAXN];
void Eratosthenes(){
	fill(bMarked,bMarked+MAXN,false);
	int nCount=0;
	for(int i=2;i<MAXN;i++){
		if(!bMarked[i]){
			prime[nCount++]=i;
			for(int j=i+i;j<MAXN;j+=i){
				bMarked[j]=true;
			}
		}
	}
}//O(nloglogn)

//Euler
const int MAXN=101;
int prime[MAXN];
bool bMarked[MAXN];
void Euler(){
	fill(bMarked,bMarked+MAXN,false);
	int nCount=0;
	for(int i=2;i<MAXN;i++){
		if(!bMarked[i]){
			bMarked[i]=true;
			prime[nCount++]=i;
		}
		for(int j=0;j<nCount&&i*prime[j]<MAXN;j++){
			bMarked[i*prime[j]]=true;
			if(i%prime[j]==0) break;
		}
	}
}O(n)

素数

题目描述
输入一个整数n(2<=n<=10000)，要求输出所有从1到这个整数之间(不包括1和这个整数)个位为1的素数，如果没有则输出-1。
输入
输入有多组数据。
每组一行，输入n。
输出
输出所有从1到这个整数之间(不包括1和这个整数)个位为1的素数(素数之间用空格隔开，最后一个素数后面没有空格)，如果没有则输出-1。
样例输入
70
样例输出
11 31 41 61
程序

#include<iostream>
#include<vector>
using namespace std;

const int MAXN=10001;
vector<int> vec;
int bMarked[MAXN];

void Euler(){
	fill(bMarked,bMarked+MAXN,false);
	for(int i=2;i<MAXN;i++){
		if(!bMarked[i]){
			bMarked[i]=true;
			vec.push_back(i);
		}
		for(int j=0;j<vec.size()&&i*vec[j]<MAXN;j++){
			bMarked[i*vec[j]]=true;
			if(i%vec[j]==0) break;
		}
	}
}

int main(){
	Euler();
	int n;
	while(cin>>n){
		bool bFirst=true;
		for(int i=0;i<vec.size()&&vec[i]<n;i++){
			int tmp=vec[i]%10;
			if(tmp==1){
				if(bFirst) bFirst=false;
				else cout<<" ";
				cout<<vec[i];
			}
		}
		if(bFirst) cout<<-1;
		cout<<endl;
	}
	return 0;
}

Prime Number

题目描述
Output the k-th prime number.
输入
k≤10000
输出
The k-th prime number.
样例输入
10
50
样例输出
29
229
程序

#include<iostream>
#include<vector>
using namespace std;

const long MAXN=9999999;
vector<int> vec;
bool bMarked[MAXN];

void Euler(){
	fill(bMarked,bMarked+MAXN,false);
	for(long i=2;vec.size()<10001;i++){
		if(!bMarked[i]){
			bMarked[i]=true;
			vec.push_back(i);
		}
		for(int j=0;j<vec.size()&&i*vec[j]<MAXN;j++){
			bMarked[i*vec[j]]=true;
			if(i%vec[j]==0) break;
		}
	}
}

int main(){
	Euler();
	int k;
	while(cin>>k){
		cout<<vec[k-1]<<endl;
	}
	return 0;
}

Goldbach’s Conjecture

Description
Goldbach’s Conjecture: For any even number n greater than or equal to 4, there exists at least one pair of prime numbers p1 and p2 such that $n = p1 + p2$.
This conjecture has not been proved nor refused yet. No one is sure whether this conjecture actually holds. However, one can find such a pair of prime numbers, if any, for a given even number. The problem here is to write a program that reports the number of all the pairs of prime numbers satisfying the condition in the conjecture for a given even number.
A sequence of even numbers is given as input. Corresponding to each number, the program should output the number of pairs mentioned above. Notice that we are interested in the number of essentially different pairs and therefore you should not count $(p1, p2)$ and $(p2, p1)$ separately as two different pairs.
Input
An integer is given in each input line. You may assume that each integer is even, and is greater than or equal to 4 and less than $2^{15}$. The end of the input is indicated by a number 0.
Output
Each output line should contain an integer number. No other characters should appear in the output.
Sample Input
4
10
16
0
Sample Output
1
2
2
Procedure

#include<iostream>
#include<vector>
#include<cmath>
using namespace std;

const int MAXN=32768;
vector<int> vec;
bool bMarked[MAXN];

void Euler(){

	fill(bMarked,bMarked+MAXN,false);
	for(int i=2;i<MAXN;i++){
		if(!bMarked[i]){
			bMarked[i]=true;
			vec.push_back(i);
		}
		for(int j=0;j<vec.size()&&i*vec[j]<MAXN;j++){
			bMarked[i*vec[j]]=true;
			if(i%vec[j]==0) break;
		}
	}
}

bool isPrime(int x){
	if(x==1) return false;
	for(int i=2;i*i<=x;i++){
		if(x%i==0) return false;
	}
	return true;
}

int main(){
	Euler();
	int n;
	while(cin>>n&&n!=0){
		int nCount=0;
		for(int i=0;i<vec.size()&&vec[i]<=n/2;i++){
			if(isPrime(n-vec[i])) nCount++;
		}
		cout<<nCount<<endl;
	}
	return 0;
}

完数

题目描述
求1-n内的完数，所谓的完数是这样的数，它的所有因子相加等于它自身，比如6有3个因子1,2,3,1+2+3=6，那么6是完数。即完数是等于其所有因子相加和的数。
输入
测试数据有多组，输入n，n数据范围不大。
输出
对于每组输入,请输出1-n内所有的完数。如有案例输出有多个数字，用空格隔开，输出最后不要有多余的空格。
样例输入
6
样例输出
6
程序

#include<iostream>
using namespace std;

bool isPerfect(int x){
	int sum=0;
	for(int i=1;i*i<=x;i++){
		if(x%i==0){
			if(i<x) sum+=i;
			if(x/i<x) sum+=x/i;
		}
		if(sum>x) return false;
	}
	if(sum==x) return true;
	else return false;
}
int main(){
	int n;
	while(cin>>n){
		int sum=0;
		bool bFirst=true;
		for(int i=1;i<=n;i++){
			if(isPerfect(i)){
				if(bFirst) bFirst=false;
				else cout<<" ";
				cout<<i;
			}
		}
		cout<<endl;
	}
	return 0;
}

质因数的个数

题目描述
求正整数N(N>1)的质因数的个数。
相同的质因数需要重复计算。如120=22235，共有5个质因数。
输入
可能有多组测试数据，每组测试数据的输入是一个正整数N，(1<N<10^9)。
输出
对于每组数据，输出N的质因数的个数。
样例输入
120
200
样例输出
5
5
程序

/*
①2~sqrt(n)如果n不等于1，说明n有且仅有一个大于sqrt(n)的质因数
*/
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

const int MAXN=100000;
vector<int> vec;
bool bMarked[MAXN];

void Euler(){
	fill(bMarked,bMarked+MAXN,false);
	for(int i=2;i<MAXN;i++){
		if(!bMarked[i]){
			bMarked[i]=true;
			vec.push_back(i);
		}
		for(int j=0;j<vec.size()&&i*vec[j]<MAXN;j++){
			bMarked[i*vec[j]]=true;
			if(i%vec[j]==0) break;
		}
	}
}

int main(){
	Euler();
	int n;
	while(cin>>n){
		int nCount=0;
		for(int i=0;i<vec.size();i++){

			while(n%vec[i]==0){
				nCount++;
				n/=vec[i];
			}
			if(n==0) break;
		}
		if(n!=1) nCount++;
		cout<<nCount<<endl;
	}
	return 0;
}

约数的个数

题目描述
输入n个整数,依次输出每个数的约数的个数。
输入
输入的第一行为N，即数组的个数(N<=1000)
接下来的1行包括N个整数，其中每个数的范围为(1<=Num<=1000000000)
当N=0时输入结束。
输出
可能有多组输入数据，对于每组输入数据，
输出N行，其中每一行对应上面的一个数的约数的个数。
样例输入
6
1 4 6 8 10 12
0
样例输出
1
3
4
4
4
6
程序

#include<iostream>
using namespace std;

int n;
int count(int x){
	int sum=0;
	for(int i=1;i*i<=x;i++){
		if(x%i==0){
			if(i*i==x) sum+=1;
			else sum+=2;
		}
	}

	return sum;
}
int main(){
	while(scanf("%d",&n)&&n!=0){
		for(int i=0;i<n;i++){
			int tmp;
			scanf("%d",&tmp);
			printf("%d\n",count(tmp));
		}

	}
	return 0;
}

完数与盈数

题目描述
一个数如果恰好等于它的各因子（该数本身除外）子和，如：6=3+2+1，则称其为“完数”；
若因子之和大于该数，则称其为“盈数”。求出2 到60 之间所有“完数”和“盈数”，并以如
下形式输出： E: e1 e2 e3 ……(ei 为完数) G: g1 g2 g3 ……(gi 为盈数)
输入
无
输出
按描述要求输出（注意EG后面的冒号之后有一个空格）。
程序

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

vector<int> vecE;
vector<int> vecG;

bool isPerfect(int x){
	int sum=0;
	for(int i=1;i*i<=x;i++){
		if(x%i==0){
			sum+=i;
			if(x/i<x) sum+=x/i;
		}
		if(sum>x) return false;
	}
	if(sum!=x) return false;
	return true;
}

int main(){

	for(int i=2;i<=60;i++){
		if(isPerfect(i)) vecE.push_back(i);
		else vecG.push_back(i);
	}
	cout<<"E:";
	for(vector<int>::iterator it=vecE.begin();it!=vecE.end();it++){
		cout<<" "<<*it;
	}
	cout<<"G:";
	for(vector<int>::iterator it=vecG.begin();it!=vecG.end();it++){
		cout<<" "<<*it;
	}
	cout<<endl;
	return 0;
}

大整数

模板

#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
using namespace std;

struct BigInteger{
	int b[1000];  //数组
	int len;
	BigInteger(){
		memset(b,0,sizeof(b));
		len=0;
	}
	BigInteger(const string &str){
		cout<<str<<endl;
		len=str.length();
		memset(b,0,sizeof(b));
		for(int i=0;i<len;i++){
			b[i]=str[len-i-1]-'0';
			cout<<b[i]<<endl;
		}
		cout<<len<<endl;
	}
	void print(){
		for(int i=len-1;i>=0;i--){
			cout<<b[i]<<":";
		}
		cout<<endl;
	}
};

int compare(BigInteger big1,BigInteger big2){
	if(big1.len>big2.len) return 1;
	else if(big1.len<big2.len) return -1;
	else{
		for(int i=big1.len-1;i>=0;i--){
			if(big1.b[i]>big2.b[i]) return 1;
			else if(big1.b[i]<big2.b[i]) return -1;
		}
		return 0;
	}
}

BigInteger addition(BigInteger big1,BigInteger big2){
	BigInteger big;
	int carry=0;
	for(int i=0;i<big1.len||i<big2.len;i++){
		int temp=big1.b[i]+big2.b[i]+carry;
		big.b[big.len++]=temp%10;
		carry=temp/10;
	}
	if(carry!=0){
		big.b[big.len++]=carry;
	}
	return big;
}

BigInteger subtraction(BigInteger big1,BigInteger big2){
	BigInteger big;
	for(int i=0;i<big1.len||i<big2.len;i++){
		if(big1.b[i]<big2.b[i]){
			big1.b[i+1]--;
			big1.b[i]+=10;
		}
		big.b[big.len++]=big1.b[i]-big2.b[i];
	}
	while(big.len>1&&big.b[big.len-1]==0){
		big.len--;
	}
	return big;
}

BigInteger mutiple(BigInteger big1,int b){
	BigInteger big;
	int carry=0
	for(int i=0;i<big1.len;i++){
		int temp=big1.b[i]*b+carry;
		big.b[big.len++]=tem%10;
		carry=temp/10;
	}
	while(carry!=0){
		big.b[big.len++]=carry%10;
		carry/=10;
	}
	return big;
}

BigInteger division(BigInteger big1, int b){
	BigInteger big;
	int rest=0;
	big.len=big1.len;
	for(int i=big1.len-1;i>=0;i--){
		rest=rest*10+big1.b[i];
		if(rest>=b){
			big.b[i]=rest/b;
			rest=rest%b;
		}else{
			big.b[i]=0;
		}
	}
	while(big.len>1&&big.b[big.len-1]==0){
		big.len--;
	}
	return big;
}

a+b

题目描述
实现一个加法器，使其能够输出a+b的值。
输入
输入包括两个数a和b，其中a和b的位数不超过1000位。
输出
可能有多组测试数据，对于每组数据，
输出a+b的值。
样例输入
6 8
2000000000 30000000000000000000
样例输出
14
30000000002000000000
程序

#include<iostream>
#include<cstring>
using namespace std;

struct BigInteger{
	int b[1001];
	int len;
	BigInteger(){
		memset(b,0,sizeof(b));
		len=0;
	}
	BigInteger(const string &str){
		memset(b,0,sizeof(b));
		len=str.length();
		for(int i=0;i<str.length();i++){
			b[i]=str[str.length()-1-i]-'0';
		}
	}
	BigInteger(const BigInteger &big){
		memset(b,0,sizeof(b));
		len=big.len;
		for(int i=0;i<len;i++){
			b[i]=big.b[i];
		}
	}
	BigInteger& operator = (const BigInteger & big){
		memset(b,0,sizeof(b));
		len=big.len;
		for(int i=0;i<len;i++){
			b[i]=big.b[i];
		}
		return *this;
	}
	void print(){
		for(int i=len-1;i>=0;i--){
			cout<<b[i];
		}
		cout<<endl;
	}
};

int compare(BigInteger big1,BigInteger big2){
	if(big1.len>big2.len) return 1;
	else if(big1.len<big2.len) return -1;
	else{
		for(int i=big1.len-1;i>=0;i--){
			if(big1.b[i]>big2.b[i]) return 1;
			else if(big1.b[i]<big2.b[i]) return -1;
		}
		return 0;
	}
}

BigInteger addition(BigInteger big1,BigInteger big2){
	BigInteger big;
	int carry=0;
	for(int i=0;i<big1.len||i<big2.len;i++){
		int temp=big1.b[i]+big2.b[i]+carry;
		big.b[big.len++]=temp%10;
		carry=temp/10;
	}
	if(carry!=0){
		big.b[big.len++]=carry;
	}
	return big;
}

BigInteger subtraction(BigInteger big1,BigInteger big2){
	BigInteger big;
	int lend=0;
	for(int i=0;i<big1.len||big2.len;i++){
		big1.b[i]-=lend;
		if(big1.b[i]<big2.b[i]){
			lend=1;
			big1.b[i]+=10;
		}
		big.b[big.len++]=big1.b[i]-big2.b[i];
	}
	while(big.len>=2&&big.b[big.len-1]==0){
		big.len--;
	}
	return big;
}

int main(){
	string a,b;
	while(cin>>a>>b){
		bool flag1,flag2;
		flag1=flag2=true;
		if(a[0]=='-') {
			flag1=false;
			a=a.substr(1,a.length()-1);
		}
		if(b[0]=='-'){
			flag2=false;
			b=b.substr(1,b.length()-1);
		}
		BigInteger big1(a),big2(b);

		if(flag1==flag2){
			BigInteger big=addition(big1,big2);
			if(!flag1) cout<<"-";
			big.print();
		}else{
			bool former=compare(big1,big2);
			BigInteger big;
			bool flag;
			if(former){
				flag=flag1;
				big=subtraction(big1,big2);
			}else{
				flag=flag2;
				big=subtraction(big2,big1);
			}
			if(big.len!=1){
				cout<<"-";
			}
			big.print();
		}
	}
	return 0;
}

组合数

n！含质因子p的个数

1.公式$n/p+n/p^{2}+n/p^{3}+…$

int cal(int n,int p){
  int ans=0;
  while(n!=0){
    ans+=n/p;
    n/=p;
  }
  return ans;
}

2.公式$f(n)=(n/p+f(n/p))$

int cal(int n,int p){
  if(n<p) return 0;
  else n/p+cal(n/p,p);
}

深度优先搜索

全排列

题目描述
排列与组合是常用的数学方法。
先给一个正整数 ( 1 < = n < = 10 )
例如n＝3，所有组合,并且按字典序输出：
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
输入
输入一个整数n( 1<=n<=10)
输出
输出所有全排列
每个全排列一行，相邻两个数用空格隔开（最后一个数后面没有空格）
样例输入
3
样例输出
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
程序

#include<iostream>
#include<cstring>
using namespace std;

int n;
bool bVisited[11];
string str;

void DFS(){
	if(str.length()==n){
		for(int i=0;i<n;i++){
			if(i!=0) cout<<" ";
			cout<<str[i];
		}
		cout<<endl;
		return;
	}
	for(int i=1;i<=n;i++){
		if(!bVisited[i]){
			str+=i+'0';
			bVisited[i]=true;
			DFS();
			str.erase(str.length()-1,1);
			bVisited[i]=false;
		}
	}
}

int main(){
	while(cin>>n){
		DFS();
	}
	return 0;
}

组合的输出

题目描述
排列与组合是常用的数学方法，其中组合就是从n个元素中抽出r个元素(不分顺序且r < ＝ n)，我们可以简单地将n个元素理解为自然数1，2，…，n，从中任取r个数。
现要求你不用递归的方法输出所有组合。
例如n ＝ 5 ，r ＝ 3 ，所有组合为：
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5
输入
一行两个自然数n、r ( 1 < n < 21，1 < ＝ r < ＝ n )。
输出
所有的组合，每一个组合占一行且其中的元素按由小到大的顺序排列，所有的组合也按字典顺序。
程序

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

int n;
int r;
string str;

void DFS(int i){
	if(str.length()==r){

		for(int i=0;i<r;i++){
			if(i!=0) cout<<" ";
			cout<<str[i]-'0';
		}
		cout<<endl;
		return;
	}
	if(i<=n){
		str+=i+'0';
		DFS(i+1);
		str.erase(str.length()-1,1);
		DFS(i+1);
	}

}
int main(){
	while(cin>>n>>r){
		DFS(1);
	}
	return 0;
}

组合+判断素数

题目描述
已知 n 个整数b1,b2,…,bn以及一个整数 k（k＜n）。
从 n 个整数中任选 k 个整数相加，可分别得到一系列的和。
例如当 n=4，k＝3，4 个整数分别为 3，7，12，19 时，可得全部的组合与它们的和为：
3＋7＋12=22　　3＋7＋19＝29　　7＋12＋19＝38　　3＋12＋19＝34。
现在，要求你计算出和为素数共有多少种。例如上例，只有一种的和为素数：3＋7＋19＝29。
输入
第一行两个整数：n , k （1<=n<=20，k＜n）
第二行n个整数：x1,x2，…,xn （1<=xi<=5000000）
输出
一个整数（满足条件的方案数）。
样例输入*
4 3
3 7 12 19
样例输出
1
程序

#include<iostream>
#include<queue>
using namespace std;

int n,k;
int nCount;
deque<int> dq;
vector<int> vec;
bool isPrime(int x){
	if(x<=1) return false;
	for(int i=2;i*i<=x;i++){
		if(x%i==0) return false;
	}
	return true;
}
void DFS(int i){
	if(dq.size()==k){
		int sum=0;
		for(int i=0;i<dq.size();i++){
			sum+=dq[i];
		}
		if(isPrime(sum)){
			nCount++;
		}
		return;
	}
	if(i<n){
		dq.push_back(vec[i]);
		DFS(i+1);
		dq.pop_back();
		DFS(i+1);
	}
}
int main(){
	while(cin>>n>>k){
		vec.resize(n);
		nCount=0;
		for(int i=0;i<n;i++){
			cin>>vec[i];
		}
		DFS(0);
		cout<<nCount<<endl;
	}
	return 0;
}

深度优先搜多

n皇后问题

题目描述
会下国际象棋的人都很清楚：皇后可以在横、竖、斜线上不限步数地吃掉其他棋子。如何将8个皇后放在棋盘上（有8 * 8个方格），使它们谁也不能被吃掉！这就是著名的八皇后问题。
输入
一个整数n（ 1 < = n < = 10 )
输出
每行输出对应一种方案，按字典序输出所有方案。每种方案顺序输出皇后所在的列号，相邻两数之间用空格隔开。如果一组可行方案都没有，输出“no solute!”
样例输入
4
样例输出
2 4 1 3
3 1 4 2
程序

#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;

int n;
bool bMarked[11];
int result[11];
int nCount;
void DFS(int row){
	if(row==n+1){
		for(int i=1;i<=n;i++){
			if(i!=1) cout<<" ";
			cout<<result[i];
		}
		cout<<endl;
		nCount++;
		return;
	}
	for(int i=1;i<=n;i++){
		if(!bMarked[i]){
			bool bPass=true;
			for(int j=1;j<row;j++){
				if(abs(result[j]-i)==abs(row-j)){
					bPass=false;
					break;
				}
			}
			if(bPass){
				result[row]=i;
				bMarked[i]=true;
				DFS(row+1);
				bMarked[i]=false;
				result[row]=0;
			}
		}
	}
}
int main(){
	while(cin>>n){
		fill(bMarked,bMarked+11,false);
		fill(result,result+11,0);
		nCount=0;
		DFS(1);
		if(nCount==0) cout<<"no solute!"<<endl;
	}
	return 0;
}

出栈序列统计

题目描述
栈是常用的一种数据结构，有n令元素在栈顶端一侧等待进栈，栈顶端另一侧是出栈序列。你已经知道栈的操作有两•种：push和pop，前者是将一个元素进栈，后者是将栈顶元素弹出。现在要使用这两种操作，由一个操作序列可以得到一系列的输出序列。请你编程求出对于给定的n，计算并输出由操作数序列1，2，…，n，经过一系列操作可能得到的输出序列总数。
输入
一个整数n（1<=n<=15）
输出
一个整数，即可能输出序列的总数目。
样例输入
3
样例输出
5
程序

#include<iostream>
#include<stack>
using namespace std;
/*
设f(i,j,k)，i表示入栈数，j表示未入栈数，k表示出栈数
那么对于当前栈：
①如果栈非空，则可以出栈和入栈
②栈空，只能入栈
所以对应出栈序列总数：
①f(i,j,k)=f(i-1,j,k+1)+f(i+1,j-1,k)
② f(i,j,k)=f(i+1,j-1,k)
边界条件：f(i,0,k)=1 入栈数为空，则出栈序列一定！
*/
int n;
int simulate(int i,int j,int k){
	if(j==0) return 1;
	if(i>0) return simulate(i-1,j,k+1)+simulate(i+1,j-1,k);
	else return simulate(i+1,j-1,k);
}
int main(){
	while(cin>>n){
		cout<<simulate(0,n,0)<<endl;
	}
	return 0;
}

如果是让求出栈序列，代码如下

#include<iostream>
#include<algorithm>
#include<vector>
#include<deque>
using namespace std;

/*
①栈非空；
当前栈顶元素，要么出栈，要么不出栈，新元素入栈
②栈空：
只能新元素入栈

函数参数i表示新元素

当i等于n+1时，表示所有元素已经操作完毕，递归截止
否则：
	①栈空，新元素入栈，进入下一次递归
	②栈非空，
		1.栈顶元素最多可以出栈x次至空栈，然后入栈
		2.复位，新元素入栈
*/
int N;
int nCount;
vector<int> vec;
void simulate(int n, deque<int> dq){
	if(n==N+1){
		for(int i=0;i<nCount;i++){
			cout<<vec[i];
		}
		for(int i=dq.size()-1;i>=0;i--){
			cout<<dq[i];
		}
		cout<<endl;
		return;
	}
	if(dq.empty()){
		dq.push_back(n);
		simulate(n+1,dq);
	}else{

		for(int i=1;i<=dq.size();i++){
			int tmpI=i;
			deque<int> tmpDq=dq;
			while(tmpI){
				vec[nCount++]=tmpDq.back();
				tmpDq.pop_back();
				tmpI--;
			}
			tmpDq.push_back(n);
			simulate(n+1,tmpDq);
			nCount-=i;
		}
		dq.push_back(n);
		simulate(n+1,dq);
	}
}
int main(){
	while(cin>>N){
		nCount=0;
		deque<int> dq;
		vec.resize(N);
		simulate(1,dq);
	}
	return 0;
}

走迷宫

题目描述
　　有一个nm格的迷宫(表示有n行、m列)，其中有可走的也有不可走的，如果用1表示可以走，0表示不可以走，文件读入这nm个数据和起始点、结束点(起始点和结束点都是用两个数据来描述的，分别表示这个点的行号和列号)。现在要你编程找出所有可行的道路，要求所走的路中没有重复的点，走时只能是上下左右四个方向。如果一条路都不可行，则输出相应信息(用-l表示无路)。
　　请统一用 左上右下的顺序拓展，也就是 (0,-1),(-1,0),(0,1),(1,0)
输入**
第一行是两个数n，m( 1 < n ， m < 15 )，接下来是m行n列由1和0组成的数据，最后两行是起始点和结束点。

输出
　　所有可行的路径，描述一个点时用(x，y)的形式，除开始点外，其他的都要用“->”表示方向。
　　如果没有一条可行的路则输出-1。

样例输入
5 6
1 0 0 1 0 1
1 1 1 1 1 1
0 0 1 1 1 0
1 1 1 1 1 0
1 1 1 0 1 1
1 1
5 6
样例输出
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(2,5)->(3,5)->(3,4)->(3,3)->(4,3)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(2,5)->(3,5)->(3,4)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(2,5)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(3,4)->(3,3)->(4,3)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(3,4)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(3,4)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(3,4)->(2,4)->(2,5)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(3,4)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(3,4)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(4,3)->(4,4)->(3,4)->(2,4)->(2,5)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(4,3)->(4,4)->(3,4)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(4,3)->(4,4)->(4,5)->(5,5)->(5,6)
程序

//按固定顺序搜索！看清题目！垃圾OJ！
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;

struct Node{
	int x,y;
	Node(){}
	Node(int X,int Y):x(X),y(Y){}
	void print(){
		cout<<"("<<x+1<<","<<y+1<<")";
	}
};
int iMap[15][15];
bool bVisited[15][15];
deque<Node> dq;
int n,m;
Node node_Enter,node_Exit;
bool bExist;
int step[4][2]={
	0,-1,
	-1,0,
	0,1,
	1,0
};
bool isPass(Node node){
	if(node.x<0||node.x>=n||node.y<0||node.y>=m) return false;
	if(iMap[node.x][node.y]==0||bVisited[node.x][node.y]) return false;
	return true;
}
void DFS(Node node){
	if(node.x==node_Exit.x&&node.y==node_Exit.y){
		bExist=true;
		for(int i=0;i<dq.size();i++){
			if(i!=0) cout<<"->";
			dq[i].print();
		}
		cout<<endl;
		return;
	}
	for(int i=0;i<4;i++){
		Node tmp;
		tmp.x=node.x+step[i][0];
		tmp.y=node.y+step[i][1];
		if(isPass(tmp)){
			bVisited[tmp.x][tmp.y]=true;
			dq.push_back(tmp);
			DFS(tmp);
			bVisited[tmp.x][tmp.y]=false;
			dq.pop_back();
		}
	}
}
int main(){

	while(cin>>n>>m){
		memset(iMap,0,sizeof(iMap));
		memset(bVisited,false,sizeof(bVisited));
		dq.clear();
		bExist=false;
		for(int i=0;i<n;i++){
			for(int j=0;j<m;j++){
				cin>>iMap[i][j];
			}
		}
		cin>>node_Enter.x>>node_Enter.y;
		cin>>node_Exit.x>>node_Exit.y;

		node_Enter.x--; node_Enter.y--;
		node_Exit.x--; node_Exit.y--;

		bVisited[node_Enter.x][node_Enter.y]=true;
		dq.push_back(node_Enter); //入口进队列
		DFS(node_Enter);
		if(!bExist) cout<<-1<<endl;
	}
	return 0;
}

广度优先搜索

Jugs

Description
In the movie “Die Hard 3”, Bruce Willis and Samuel L. Jackson were confronted with the following puzzle. They were given a 3-gallon jug and a 5-gallon jug and were asked to fill the 5-gallon jug with exactly 4 gallons. This problem generalizes that puzzle.

You have two jugs, A and B, and an infinite supply of water. There are three types of actions that you can use: (1) you can fill a jug, (2) you can empty a jug, and (3) you can pour from one jug to the other. Pouring from one jug to the other stops when the first jug is empty or the second jug is full, whichever comes first. For example, if A has 5 gallons and B has 6 gallons and a capacity of 8, then pouring from A to B leaves B full and 3 gallons in A.

A problem is given by a triple (Ca,Cb,N), where Ca and Cb are the capacities of the jugs A and B, respectively, and N is the goal. A solution is a sequence of steps that leaves exactly N gallons in jug B. The possible steps are

fill A
fill B
empty A
empty B
pour A B
pour B A
success

where “pour A B” means “pour the contents of jug A into jug B”, and “success” means that the goal has been accomplished.

You may assume that the input you are given does have a solution.
Input
Input to your program consists of a series of input lines each defining one puzzle. Input for each puzzle is a single line of three positive integers: Ca, Cb, and N. Ca and Cb are the capacities of jugs A and B, and N is the goal. You can assume 0 < Ca <= Cb and N <= Cb <=1000 and that A and B are relatively prime to one another.
Output
Output from your program will consist of a series of instructions from the list of the potential output lines which will result in either of the jugs containing exactly N gallons of water. The last line of output for each puzzle should be the line “success”. Output lines start in column 1 and there should be no empty lines nor any trailing spaces.
Sample Input
3 5 4
5 7 3
Sample Output
fill B
pour B A
empty A
pour B A
fill B
pour B A
success
fill A
pour A B
fill A
pour A B
empty B
pour A B
success
Procedure

#include<iostream>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;

int A,B,N;
struct Node{
	int i,j;
	int father;
	int operators;
	Node(){}
	Node(int ii,int jj,int ff,int oo):i(ii),j(jj),father(ff),operators(oo){}
};
deque<Node> que;
vector<Node> vec;
bool bVisited[1001][1001];
string result[6]={
	"fill A",
	"fill B",
	"empty A",
	"empty B",
	"pour A B",
	"pour B A"
};
void print(Node tmp){
	vector<string> v;
	while(tmp.father!=-1){
		v.push_back(result[tmp.operators]);
		tmp=vec[tmp.father];
	}
	for(vector<string>::reverse_iterator it=v.rbegin();it!=v.rend();it++){
		cout<<*it<<endl;
	}
	cout<<"success"<<endl;
}
void BFS(){
	memset(bVisited,false,sizeof(bVisited));
	que.clear();
	vec.clear();
	int index=-1;
	bVisited[0][0]=true;
	que.push_back(Node(0,0,index,-1));
	vec.push_back(Node(0,0,index,-1));
	index++;
	while(!que.empty()){
//		for(int i=0;i<vec.size();i++){
//			cout<<vec[i].i<<":"<<vec[i].j<<":"<<vec[i].father<<":"<<vec[i].operators<<endl;
//		}
//		cout<<"---"<<endl;
		Node tmp=que.front();
		int i=tmp.i;
		int j=tmp.j;
		que.pop_front();
		if(tmp.j==N){
			print(tmp);
			return;
		}
		for(int k=0;k<6;k++){
			switch(k){
				case 0:{
					if(!bVisited[A][j]){
						bVisited[A][j]=true;
						que.push_back(Node(A,j,index,0));
						vec.push_back(Node(A,j,index,0));
					}
					break;
				}
				case 1:{
					if(!bVisited[i][B]){
						bVisited[i][B]=true;
						que.push_back(Node(i,B,index,1));
						vec.push_back(Node(i,B,index,1));
					}
					break;
				}
				case 2:{
					if(!bVisited[0][j]){
						bVisited[0][j]=true;
						que.push_back(Node(0,j,index,2));
						vec.push_back(Node(0,j,index,2));
					}
					break;
				}
				case 3:{
					if(!bVisited[i][0]){
						bVisited[i][0]=true;
						que.push_back(Node(i,0,index,3));
						vec.push_back(Node(i,0,index,3));
					}
					break;
				}
				case 4:{
					if(i+j>B){
						if(!bVisited[i-B+j][B]){
							bVisited[i-B+j][B]=true;
							que.push_back(Node(i-B+j,B,index,4));
							vec.push_back(Node(i-B+j,B,index,4));
						}
					}else{
						if(!bVisited[0][i+j]){
							bVisited[0][i+j]=true;
							que.push_back(Node(0,i+j,index,4));
							vec.push_back(Node(0,i+j,index,4));
						}
					}
					break;
				}
				case 5:{
					if(i+j>A){
						if(!bVisited[A][j-A+i]){
							bVisited[A][j-A+i]=true;
							que.push_back(Node(A,j-A+i,index,5));
							vec.push_back(Node(A,j-A+i,index,5));
						}
					}else{
						if(!bVisited[i+j][0]){
							bVisited[i+j][0]=true;
							que.push_back(Node(i+j,0,index,5));
							vec.push_back(Node(i+j,0,index,5));
						}
					}
					break;
				}
			}
		}
		index++;
	}
}
int main(){
	while(cin>>A>>B>>N){
		BFS();
	}
	return 0;
}

并查集

通信系统

题目描述
某市计划建设一个通信系统。按照规划，这个系统包含若干端点，这些端点由通信线缆链接。消息可以在任何一个端点产生，并且只能通过线缆传送。每个端点接收消息后会将消息传送到与其相连的端点，除了那个消息发送过来的端点。如果某个端点是产生消息的端点，那么消息将被传送到与其相连的每一个端点。
为了提高传送效率和节约资源，要求当消息在某个端点生成后，其余各个端点均能接收到消息，并且每个端点均不会重复收到消息。
现给你通信系统的描述，你能判断此系统是否符合以上要求吗？
输入
输入包含多组测试数据。每两组输入数据之间由空行分隔。
每组输入首先包含2个整数N和M，N（1<=N<=1000）表示端点个数，M（0<=M<=N(N-1)/2）表示通信线路个数。
接下来M行每行输入2个整数A和B（1<=A，B<=N），表示端点A和B由一条通信线缆相连。两个端点之间至多由一条线缆直接相连，并且没有将某个端点与其自己相连的线缆。
当N和M都为0时，输入结束。
*输出**
对于每组输入，如果所给的系统描述符合题目要求，则输出Yes，否则输出No。
样例输入
4 3
1 2
2 3
3 4

3 1
2 3

0 0
样例输出
Yes
No
程序

#include<iostream>
using namespace std;

//并查集
//需要判断是否成环：
//如果两个点已在同一个集合中，在连接一条边比成环；
//否则不成环

int father[1001];
int M,N;
bool isLoop;
int count;
void makeSet(){
	count=M;
	isLoop=false;
	for(int i=1;i<=M;i++){
		father[i]=i;
	}
}

int findFather(int i){
	if(i!=father[i]){
		father[i]=findFather(father[i]);
	}
	return father[i];
}

void unionSet(int i,int j){
	int fa=findFather(i);
	int fb=findFather(j);
	if(fa==fb){
		isLoop=true;
	}else{
		count--;
		father[fa]=fb;
	}
}

int main(){
	while(cin>>M>>N&&(M!=0||N!=0)){
		makeSet();
		for(int i=0;i<N;i++){
			int x,y;
			cin>>x>>y;
			unionSet(x,y);
		}
		if(count==1&&!isLoop){
			cout<<"Yes"<<endl;
		}else{
			cout<<"No"<<endl;
		}
	}
	return 0;
}

畅通工程

题目描述
某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。问最少还需要建设多少条道路？
输入
测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数，分别是城镇数目N ( < 1000 )和道路数目M；随后的M行对应M条道路，每行给出一对正整数，分别是该条道路直接连通的两个城镇的编号。为简单起见，城镇从1到N编号。
注意:两个城市之间可以有多条道路相通,也就是说
3 3
1 2
1 2
2 1
这种输入也是合法的
当N为0时，输入结束，该用例不被处理。
输出
对每个测试用例，在1行里输出最少还需要建设的道路数目。
样例输入
5 3
1 2
3 2
4 5
0
样例输出
1
程序

#include<iostream>
using namespace std;

int N,M;
int city[1001];
int count;

void makeSet(){
	count=N;
	for(int i=1;i<=N;i++){
		city[i]=i;
	}
}
int findFather(int i){
	if(i!=city[i]){
		city[i]=findFather(city[i]);
	}
	return city[i];
}

void unionSet(int i,int j){
	int fa=findFather(i);
	int fb=findFather(j);
	if(fa!=fb){
		city[fa]=fb;
		count--;
	}
}
int main(){
	while(cin>>N&&N!=0){
		cin>>M;
		makeSet();
		for(int i=0;i<M;i++){
			int x,y;
			cin>>x>>y;
			unionSet(x,y);
		}
		cout<<count-1<<endl;
	}
	return 0;
}

How Many Tables

Description
Today is Ignatius’ birthday. He invites a lot of friends. Now it’s dinner time. Ignatius wants to know how many tables he needs at least. You have to notice that not all the friends know each other, and all the friends do not want to stay with strangers.
One important rule for this problem is that if I tell you A knows B, and B knows C, that means A, B, C know each other, so they can stay in one table.
For example: If I tell you A knows B, B knows C, and D knows E, so A, B, C can stay in one table, and D, E have to stay in the other one. So Ignatius needs 2 tables at least.
Input
The input starts with an integer T(1<=T<=25) which indicate the number of test cases. Then T test cases follow. Each test case starts with two integers N and M(1<=N,M<=1000). N indicates the number of friends, the friends are marked from 1 to N. Then M lines follow. Each line consists of two integers A and B(A!=B), that means friend A and friend B know each other. There will be a blank line between two cases.
Output
For each test case, just output how many tables Ignatius needs at least. Do NOT print any blanks.
Sample Inout
2
6 4
1 2
2 3
3 4
1 4

8 10
1 2
2 3
5 6
7 5
4 6
3 6
6 7
2 5
2 4
4 3
Sample Output
3
2
Procedure

#include<iostream>
using namespace std;

int N,M;
int city[1001];
int count;

void makeSet(){
	count=N;
	for(int i=1;i<=N;i++){
		city[i]=i;
	}
}
int findFather(int i){
	if(i!=city[i]){
		city[i]=findFather(city[i]);
	}
	return city[i];
}

void unionSet(int i,int j){
	int fa=findFather(i);
	int fb=findFather(j);
	if(fa!=fb){
		city[fa]=fb;
		count--;
	}
}
int main(){
	while(cin>>N&&N!=0){
		cin>>M;
		makeSet();
		for(int i=0;i<M;i++){
			int x,y;
			cin>>x>>y;
			unionSet(x,y);
		}
		cout<<count-1<<endl;
	}
	return 0;
}

More is better

Description
Mr Wang wants some boys to help him with a project. Because the project is rather complex, the more boys come, the better it will be. Of course there are certain requirements.Mr Wang selected a room big enough to hold the boys. The boy who are not been chosen has to leave the room immediately. There are 10000000 boys in the room numbered from 1 to 10000000 at the very beginning. After Mr Wang’s selection any two of them who are still in this room should be friends (direct or indirect), or there is only one boy left. Given all the direct friend-pairs, you should decide the best way.
Input
The first line of the input contains an integer n (0 ≤ n ≤ 100 000) - the number of direct friend-pairs. The following n lines each contains a pair of numbers A and B separated by a single space that suggests A and B are direct friends. (A ≠ B, 1 ≤ A, B ≤ 10000000)
Output
The output in one line contains exactly one integer equals to the maximum number of boys Mr Wang may keep.
Sample Input
3
1 3
1 5
2 5
4
3 2
3 4
1 6
2 6
Sample Output
4
5
Procedure

#include<iostream>
using namespace std;

struct Node{
	int father;
	int count;
	Node(){}
	Node(int f,int c):father(f),count(c){}
};
const int MAX=10000001;
Node nodes[MAX];
int n;
int maxN;

void makeSet(){
	maxN=1;
	for(int i=1;i<MAX;i++){
		nodes[i].father=i;
		nodes[i].count=1;
	}
}

int findFather(int i){
	if(i!=nodes[i].father){
		nodes[i].father=findFather(nodes[i].father);
	}
	return nodes[i].father;
}

void unionSet(int i,int j){
	int fa=findFather(i);
	int fb=findFather(j);
	if(fa!=fb){
		nodes[fa].father=fb;
		nodes[fb].count+=nodes[fa].count;
		if(nodes[fb].count>maxN){
			maxN=nodes[fb].count;
		}
	}
}

int main(){
	while(cin>>n){
		makeSet();
		for(int i=0;i<n;i++){
			int x,y;
			cin>>x>>y;
			unionSet(x,y);
		}
		cout<<maxN<<endl;
	}
	return 0;
}

PAT1034 Head of a Gang

Description
One way that the police finds the head of a gang is to check people’s phone calls. If there is a phone call between A and B, we say that A and B is related. The weight of a relation is defined to be the total time length of all the phone calls made between the two persons. A “Gang” is a cluster of more than 2 persons who are related to each other with total relation weight being greater than a given threthold K. In each gang, the one with maximum total weight is the head. Now given a list of phone calls, you are supposed to find the gangs and the heads.
Input Specification
Each input file contains one test case. For each case, the first line contains two positive numbers N and K (both less than or equal to 1000), the number of phone calls and the weight threthold, respectively. Then N lines follow, each in the following format:
Name1 Name2 Time
where Name1 and Name2 are the names of people at the two ends of the call, and Time is the length of the call. A name is a string of three capital letters chosen from A-Z. A time length is a positive integer which is no more than 1000 minutes.
Output Specification
For each test case, first print in a line the total number of gangs. Then for each gang, print in a line the name of the head and the total number of the members. It is guaranteed that the head is unique for each gang. The output must be sorted according to the alphabetical order of the names of the heads.
Sample Input 1
8 59
AAA BBB 10
BBB AAA 20
AAA CCC 40
DDD EEE 5
EEE DDD 70
FFF GGG 30
GGG HHH 20
HHH FFF 10
Sample Output 1
2
AAA 3
GGG 3
Sample Input 2
8 70
AAA BBB 10
BBB AAA 20
AAA CCC 40
DDD EEE 5
EEE DDD 70
FFF GGG 30
GGG HHH 20
HHH FFF 10
Sample Output 2
0
Procedure

#include<iostream>
#include<cstring>
#include<map>
#include<set>
using namespace std;

const int MAXV=2001;
int weight[MAXV];
int N,K;
map<string,int> stringToInt;//姓名-编号
map<int,string> intToString;//编号-姓名
map<string,int> gangs;
struct Node{
	int father;
	int head;
	int count;
	int totalWeight;
};
Node nodes[MAXV];
int numPersons;
void makeSet(){
	numPersons=0;
	stringToInt.clear();
	intToString.clear();
	gangs.clear();
	memset(weight,0,sizeof(weight));

	for(int i=0;i<MAXV;i++){
		nodes[i].father=i;
		nodes[i].head=i;
		nodes[i].count=1;
		nodes[i].totalWeight=weight[i];
	}
}
int findFather(int i){
	if(i!=nodes[i].father){
		nodes[i].father=findFather(nodes[i].father);
	}
	return nodes[i].father;
}
void unionSet(int i,int j,int w){
	int fa=findFather(i);
	int fb=findFather(j);
	if(fa!=fb){
		nodes[fa].father=fb;
		nodes[fb].totalWeight+=w+nodes[fa].totalWeight;
		nodes[fb].count+=nodes[fa].count;

		//每次更新，head会在原有两个结合中的 head以及两个端点中选择 ，下同
		nodes[fb].head=(weight[nodes[fa].head]>weight[nodes[fb].head])?nodes[fa].head:nodes[fb].head;

		int wI=weight[i];
		int wJ=weight[j];
		if(wI>weight[nodes[fb].head]) nodes[fb].head=i;
		if(wJ>weight[nodes[fb].head]) nodes[fb].head=j;

//		cout<<"fb->head:"<<nodes[fb].head<<":"<<intToString[nodes[fb].head]<<" weight:"<<weight[nodes[fb].head]<<endl;
//		system("pause");
	}else{
		nodes[fa].totalWeight+=w;

		int wI=weight[i];
		int wJ=weight[j];
		if(wI>weight[nodes[fa].head]) nodes[fa].head=i;
		if(wJ>weight[nodes[fa].head]) nodes[fa].head=j;
//		cout<<"fa>head:"<<nodes[fa].head<<":"<<intToString[nodes[fa].head]<<" weight:"<<weight[nodes[fa].head]<<endl;
//		system("pause");
	}
}
int getNumber(string str){
	if(stringToInt.find(str)!=stringToInt.end()){
		return stringToInt[str];
	}else{
		stringToInt[str]=numPersons;
		intToString[numPersons]=str;
		return numPersons++;
	}
}
int main(){
	while(cin>>N>>K){
		makeSet();
		for(int i=0;i<N;i++){
			string name1,name2;
			int w;
			cin>>name1>>name2>>w;
			int num1=getNumber(name1);
			int num2=getNumber(name2);
			weight[num1]+=w;
			weight[num2]+=w;
			unionSet(num1,num2,w);
		}
		set<int> s;
		for(int i=0;i<numPersons;i++){
			int f=findFather(i);
			if(s.count(f)==0){
				s.insert(f);
			}
		}
		for(set<int>::iterator it=s.begin();it!=s.end();it++){
			int head=nodes[*it].head;
			if(nodes[*it].count>2&&nodes[*it].totalWeight>K){
				gangs[intToString[head]]=nodes[*it].count;
			}
		}

		cout<<gangs.size()<<endl;
		for(map<string,int>::iterator it=gangs.begin();it!=gangs.end();it++){
			cout<<it->first<<" "<<it->second<<endl;
		}
	}
	return 0;
}

动态规划

问题	递推公式
经典数塔问题	$dp[i][j]=max\lbrace dp[i+1][j],dp[i+1][j+1]\rbrace +data[i][j]$
最大连续子序列和	$dp[i]=max\lbrace data[i], dp[i-1]+data[i]\rbrace, dp[0]=data[0], maxSeq=max\lbrace dp[i]\rbrace$
最长不下降子序列 (Longest Increasing Sequence, LIS)	$dp[i]=max\lbrace dp[j]+1 \rbrace, start: dp[i]=1$
最长公共子序列 (Longest Common Subsequence, LCS)	$$dp[i][j]=\begin{cases} dp[i-1][j-1]+1, & \text{$A[i]==B[i]$} \\ \max\lbrace dp[i-1][j], dp[i][j-1]\rbrace, & \text{$A[i]!=B[i]$} \end{cases}$$
最长回文子串	$$dp[i][j]=\begin{cases} dp[i+1][j-1], & \text{$S[i]==S[j]$} \\ 0, & \text{$S[i]!=S[j]$} \end{cases}$$
01背包-二维-正序or逆序	$$dp[i][v]=\max\lbrace dp[i-1][v], dp[i-1][v-w[i]]+c[i]\rbrace$$
01背包-一维优化-逆序	$$dp[v]=\max\lbrace dp[v], dp[v-w[i]]+c[i]\rbrace$$
完全背包-二维-正序	$$dp[i][v]=\max\lbrace dp[i-1][v], dp[i][v-w[i]]+c[i]\rbrace$$
完全背包-一维-正序	$$dp[v]=\max\lbrace dp[v], dp[v-w[i]]+c[i]\rbrace$$

最大连续子序列

题目描述
给定K个整数的序列{ N1, N2, …, NK }，其任意连续子序列可表示为{ Ni, Ni+1, …, Nj }，其中 1 <= i <= j <= K。最大连续子序列是所有连续子序列中元素和最大的一个，例如给定序列{ -2, 11, -4, 13, -5, -2 }，其最大连续子序列为{ 11, -4, 13 }，最大和为20。现在增加一个要求，即还需要输出该子序列的第一个和最后一个元素。
输入
测试输入包含若干测试用例，每个测试用例占2行，第1行给出正整数K( K<= 10000 )，第2行给出K个整数，中间用空格分隔，每个数的绝对值不超过100。当K为0时，输入结束，该用例不被处理。
输出
对每个测试用例，在1行里输出最大和、最大连续子序列的第一个和最后一个元素，中间用空格分隔。如果最大连续子序列不唯一，则输出序号i和j最小的那个（如输入样例的第2、3组）。若所有K个元素都是负数，则定义其最大和为0，输出整个序列的首尾元素。
样例输入
5
-3 9 -2 5 -4
3
-2 -3 -1
0
样例输出
12 9 5
0 -2 -1
程序

#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;
const int MAXN=10001;
int maxSum,s,e;
int DP[MAXN];
int A[MAXN];
int k;
struct Node{
	int s,e;
};
Node Pos[MAXN];
/*
DP[i]=max(A[i],DP[i-1]+A[i])
*/
int main(){
	while(cin>>k&&k!=0){
		for(int i=0;i<k;i++){
			cin>>A[i];
		}

		bool flag=true;
		if(A[0]>=0) flag=false;
		DP[0]=A[0];
		Pos[0].s=Pos[0].e=0;

		for(int i=1;i<k;i++){
			if(A[i]>=0) flag=false;
			if(A[i]>DP[i-1]+A[i]){
				DP[i]=A[i];
				Pos[i].s=Pos[i].e=i;
			}else{
				DP[i]=DP[i-1]+A[i];
				Pos[i].s=Pos[i-1].s;
				Pos[i].e=i;
			}
		}
		int index=0;
		maxSum=DP[index];
		s=Pos[index].s;
		e=Pos[index].e;
		for(int i=1;i<k;i++){
			if(DP[i]>maxSum){
				maxSum=DP[i];
				s=Pos[i].s;
				e=Pos[i].e;
			}
		}
		if(flag){
			maxSum=0;
			s=0;
			e=k-1;
		}
		cout<<maxSum<<" "<<A[s]<<" "<<A[e]<<endl;
	}
	return 0;
}

最长上升子序列

题目描述
一个数列ai如果满足条件a1 < a2 < … < aN，那么它是一个有序的上升数列。我们取数列(a1, a2, …, aN)的任一子序列(ai1, ai2, …, aiK)使得1 <= i1 < i2 < … < iK <= N。例如，数列(1, 7, 3, 5, 9, 4, 8)的有序上升子序列，像(1, 7)， (3, 4, 8)和许多其他的子序列。在所有的子序列中，最长的上升子序列的长度是4，如(1, 3, 5, 8)。
现在你要写一个程序，从给出的数列中找到它的最长上升子序列。
输入
输入包含两行，第一行只有一个整数N（1 <= N <= 1000），表示数列的长度。
第二行有N个自然数ai，0 <= ai <= 10000，两个数之间用空格隔开。
输出
输出只有一行，包含一个整数，表示最长上升子序列的长度。
样例输入
7
1 7 3 5 9 4 8
样例输出
4
程序

#include<iostream>
#include<algorithm>
using namespace std;

//DP[i]表示以第i个元素为结尾的最长子序列长度
//DP[i]=max(DP[i],DP[j]+1) j<i且A[j]<A[i]

const int MAX=1001;
int N;
int DP[MAX];
int A[MAX];
int maxN;
int main(){
	while(cin>>N){
		fill(DP,DP+MAX,1);
		maxN=1;
		for(int i=0;i<N;i++){
			cin>>A[i];
		}
		for(int i=0;i<N;i++){
			for(int j=0;j<i;j++){
				if(A[j]<A[i]){
					DP[i]=max(DP[i],DP[j]+1);
					maxN=max(maxN,DP[i]);
				}
			}
		}
		cout<<maxN<<endl;
	}
	return 0;
}

最长公共子序列

题目描述
给你一个序列X和另一个序列Z，当Z中的所有元素都在X中存在，并且在X中的下标顺序是严格递增的，那么就把Z叫做X的子序列。
例如：Z=<a,b,f,c>是序列X=<a,b,c,f,b,c>的一个子序列，Z中的元素在X中的下标序列为<1,2,4,6>。
现给你两个序列X和Y，请问它们的最长公共子序列的长度是多少？
输入
输入包含多组测试数据。每组输入占一行，为两个字符串，由若干个空格分隔。每个字符串的长度不超过100。
输出
对于每组输入，输出两个字符串的最长公共子序列的长度。
样例输入
abcfbc abfcab
programming contest
abcd mnp
样例输出
4
2
0
程序

#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;

//DP[i][j]表示A的前i个字符串和B的前j个字符串的最大公共序列长
//假设DP[i-1][j-1]已知；
//那么DP[i][j]:
//比较A的第i个字符与B的第j个字符是否相等:
//①如果相等，直接DP[i][j]=DP[i-1][j-1];
//②如果不相等，那么比较取i，j-1和i-1，j两种情况的大小，即
//if(A[i]==B[i]) DP[i][j]=D[i-1][j-1]+1;
//else DP[i][j]=max(DP[i-1][j],DP[i][j-1]);

const int MAX=101;
string A,B;
int DP[MAX][MAX];

int main(){
	while(cin>>A>>B){
		memset(DP,0,sizeof(DP));
		for(int i=1;i<=A.size();i++){
			for(int j=1;j<=B.size();j++){
				if(A[i-1]==B[j-1]){
					DP[i][j]=DP[i-1][j-1]+1;
				}else{
					DP[i][j]=max(DP[i-1][j],DP[i][j-1]);
				}
			}
		}
		cout<<DP[A.size()][B.size()]<<endl;
	}
	return 0;
}

最长回文子串

题目描述
输入一个字符串，求出其中最长的回文子串。子串的含义是：在原串中连续出现的字符串片段。回文的含义是：正着看和倒着看相同。如abba和yyxyy。在判断回文时，应该忽略所有标点符号和空格，且忽略大小写，但输出应保持原样（在回文串的首部和尾部不要输出多余字符）。输入字符串长度不超过5000，且占据单独的一行。应该输出最长的回文串，如果有多个，输出起始位置最靠左的。
输入
一行字符串，字符串长度不超过5000。
输出
字符串中的最长回文子串。
样例输入
Confuciuss say:Madam,I’m Adam.
样例输出
Madam,I’m Adam
程序

#include<iostream>
#include<cstring>
#include<cctype>
using namespace std;

//DP[i][j]表示字符从i到j是否为回文串，是则为1，否为0；
//if(S[i]=S[j]) DP[i][j]=DP[i+1][j-1];
//else DP[i][j]=0;
//边界：
//DP[i][i]=1;

string str;
int pos[5001];
int DP[5001][5001];
int s,e,maxL;
int main(){
	while(getline(cin,str)){
		memset(DP,0,sizeof(DP));
		string ss;
		int index=0;
		for(int i=0;i<str.length();i++){
			if((str[i]>='0'&&str[i]<='9')
				||(str[i]>='a'&&str[i]<='z')){
				ss+=str[i];
				pos[index++]=i;
			}else if(str[i]>='A'&&str[i]<='Z'){
				ss+=str[i]+'a'-'A';
				pos[index++]=i;
			}
		}
		//边界
		maxL=1;
		s=e=0;
		for(int i=0;i<ss.length();i++){
			DP[i][i]=1;
			if(i<ss.length()-1){
				if(ss[i]==ss[i+1]){
					DP[i][i+1]=1;
					maxL=2;
					s=i;
					e=i+1;
				}
			}
		}
		//DP
		for(int L=3;L<=ss.length();L++){
			for(int i=0;i+L-1<ss.length();i++){
				int j=i+L-1;
				if(ss[i]==ss[j]&&DP[i+1][j-1]==1){
					DP[i][j]=1;
					if(L>maxL){
						maxL=L;
						s=i;
						e=j;
					}
				}
			}
		}
		cout<<str.substr(pos[s],pos[e]-pos[s]+1)<<endl;
	}
	return 0;
}

DAG最长路

不固定起点与终点

dp[i]表示从i号顶点出发能获得的最长路径长度
初始化：dp[i]=0;

memset(dp,0,sizeof(dp));
int DP(int i){
  if(dp[i]>0) return dp[i];
  for(int j=0;j<n;j++){
    if(G[i][j]!=INF){
      dp[i]=max(dp[i],DP(j)+G[i][j]);
    }
  }
  return dp[i];
}

打印路径：later数组，当有多条则使用vector数组

int DP(int i){
  if(dp[i]>0) return dp[i];
  for(int j=0;j<n;j++){
    if(G[i][j]!=INF){
      int temp=DP(j)+G[i][j];
      if(temp>dp[i]){
        dp[i]=temp;
        later[i]=j;
      }
    }
  }
  return dp[i];
}

void printPath(int i){
  cout<<i;
  while(later[i]!=-1){
    i=later[i];
    cout<<"->"<<i;
  }
}

固定终点

dp[i]表示从i号顶点出发到达终点T能获得的最长路径长度
初始化：dp[T]=0,其他dp[j]=-INF;

int DP(int i){
  if(vis[i]) return dp[i];
  vis[i]=true;
  for(int j=0;j<n;j++){
    if(G[i][j]!=INF){
        dp[i]=max(dp[i],DP(i)+G[i][j]);
    }
  }
  return dp[i];
}

矩形嵌套

题目描述
有n个矩形，每个矩形可以用a,b来描述，表示长和宽。矩形X(a,b)可以嵌套在矩形Y(c,d)中当且仅当a<c,b<d或者b<c,a<d（相当于旋转X90度）。例如（1,5）可以嵌套在（6,2）内，但不能嵌套在（3,4）中。你的任务是选出尽可能多的矩形排成一行，使得除最后一个外，每一个矩形都可以嵌套在下一个矩形内。
输入
第一行是一个正正数N(0<N<10)，表示测试数据组数，
每组测试数据的第一行是一个正正数n，表示该组测试数据中含有矩形的个数(n<=1000)
随后的n行，每行有两个数a,b(0<a,b<100)，表示矩形的长和宽
输出
每组测试数据都输出一个数，表示最多符合条件的矩形数目，每组输出占一行
样例输入
1
10
1 2
2 4
5 8
6 10
7 9
3 1
5 8
12 10
9 7
2 2
样例输出
5
程序

#include<iostream>
#include<algorithm>
#include<cmath>
#include<vector>
using namespace std;
const int MAXV=1001;
struct Node{
	int w;
	int h;
};
vector<Node> vec;
int DP[MAXV];
int N,n;

bool judge(Node a,Node b){
	if((a.w<b.w&&a.h<b.h)
	||(a.h<b.w&&a.w<b.h)){
		return true;
	}
	return false;
}
int main(){
	cin>>N;
	while(N--){
		cin>>n;
		vec.clear();
		vec.resize(n);
		for(int i=0;i<n;i++){
			cin>>vec[i].w>>vec[i].h;
			DP[i]=1;
		}
		int result=0;
		for(int i=0;i<n;i++){
			for(int j=0;j<i;j++){
				if(judge(vec[j],vec[i])){
					DP[i]=max(DP[i],DP[j]+1);
				}
			}
			result=max(DP[i],result);
		}
		cout<<result<<endl;
	}
	return 0;
}

背包问题

01背包

• DP[0][v]=0,DP[i][v]=max(DP[i-1][v],DP[i-1][v-w[i]]+c[i]) 正序
• DP[v]=0, DP[v]=max(DP[v],DP[v-w[i-1]]+c[i]) 逆序

  int w[MAX];
  int c[MAX];
  //通常写法
  //边界DP[0][v]=0
  int DP[MAX][MAX];
  for(int i=1;i<=n;i++){
    for(int v=w[i];v<=V;v++){
      DP[i][v]=max(DP[i-1][v],DP[i-1][v-w[i]]+c[i]);
    }
  }
  //滚动数组
  //边界DP[v]=0
  int DP[MAX]
  for(int i=1;i<=n;i++){
    for(v=V;v>=w[i];v--){
      DP[v]=max(DP[v],DP[v-w[i]]+c[i]);
    }
  }

  #include<iostream>
  #include<algorithm>
  using namespace std;
  const int MAXN=100;
  const int MAXV=1000;
  int W[MAXN],C[MAXN],DP[MAXV];
  int main(){
    int n,V;
    cin>>n>>V;
    for(int i=1;i<=n;i++) cin>>w[i];
    for(int i=1;i<=n;i++) cin>>c[i];
    //边界
    for(int v=0;v<=V;v++) DP[v]=0;
    //DP
    for(int i=1;i<=n;i++){
      for(int v=V;v>=w[i];v--){
        DP[v]=max(DP[v],DP[v-W[i]]);
      }
    }
    //寻找最大值
    int MAX=0;
    for(int v=0;v<=V;v++) MAX=DP[v]>MAX?DP[v]:MAX;
    cout<<MAX<<endl;
    return 0;
  }

  完全背包

• DP[i][v]=max(DP[i-1][v],DP[i][v-w[i]]+c[i]) 正序
• DP[v]=max(DP[v],DP[v-w[i]]+c[i]) 正序

  for(int i=1;i<=n;i++){
    for(int v=w[i];v<=V;v++){
      DP[i][v]=max(DP[i-1][v],DP[i][v-w[i]]+c[i]);
    }
  }
  
  for(int i=1;i<=n;i++){
    for(int v=w[i];v<=V;v++){
      DP[v]=max(DP[v],DP[v-w[i]]+c[i]);
    }
  }

  装箱问题

题目描述
有一个箱子的容量为V（V为正整数，且满足0≤V≤20000），同时有n件物品（0的体积值为正整数。
要求从n件物品中，选取若干装入箱内，使箱子的剩余空间最小。
输入：1行整数，第1个数表示箱子的容量，第2个数表示有n件物品，后面n个数分别表示这n件
物品各自的体积。
输出
1个整数，表示箱子剩余空间。
输入
24 6 8 3 12 7 9 7
输出
0
程序

#include<iostream>
#include<vector>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
const int MAXV=100000;

int n,V;
int DP[MAXV];
int c[MAXV];
int main(){
	while(cin>>V>>n){
		memset(DP,0,sizeof(DP));
		for(int i=1;i<=n;i++) cin>>c[i];
		for(int i=1;i<=n;i++){
			for(int v=V;v>=c[i];v--){
				DP[v]=max(DP[v],DP[v-c[i]]+c[i]);
			}
		}
		int Max=0;
		for(int v=0;v<=V;v++){
			Max=Max>DP[v]?Max:DP[v];
		}
		cout<<V-Max<<endl;
	}
	return 0;
}

采药

题目描述
辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。
医师为了判断他的资质，给他出了一个难题。
医 师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间， 在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”
如果你是辰辰，你能完成这个任务吗？
输入
第一行有两个整数T（1 <= T <= 1000）和M（1 <= M <= 100），用一个空格隔开，
T代表总共能够用来采药的时间，M代表山洞里的草药的数目。
接下来的M行每行包括两个在1到100之间（包括1和100）的整 数，分别表示采摘某株草药的时间和这株草药的价值。
输出
一个整数，表示在规定的时间内，可以采到的草药的最大总价值。
样例输入
70 3
71 100
69 1
1 2
样例输出
3
程序

#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
int T,M;
int DP[1001];
int c[101];
int v[101];

int main(){
	while(cin>>T>>M){
		memset(DP,0,sizeof(DP));
		memset(c,0,sizeof(c));
		memset(v,0,sizeof(v));
		for(int i=1;i<=M;i++) cin>>c[i]>>v[i];
		for(int i=1;i<=M;i++){
			for(int t=T;t>=c[i];t--){
				DP[t]=max(DP[t],DP[t-c[i]]+v[i]);
			}
		}
    int Max=0;
    for(int t=0;t<=T;t++)  Max=Max>DP[t]?Max:DP[t];
		cout<<Max<<endl;
	}
	return 0;
}

货币系统

题目描述
母牛们不但创建了他们自己的政府而且选择了建立了自己的货币系统。
[In their own rebellious way],，他们对货币的数值感到好奇。
传统地，一个货币系统是由1,5,10,20 或 25,50, 和 100的单位面值组成的。
母牛想知道有多少种不同的方法来用货币系统中的货币来构造一个确定的数值。
举例来说, 使用一个货币系统 {1,2,5,10,…}产生 18单位面值的一些可能的方法是:18x1, 9x2, 8x2+2x1, 3x5+2+1,等等其它。
写一个程序来计算有多少种方法用给定的货币系统来构造一定数量的面值。
保证总数将会适合long long (C/C++) 和 Int64 (Free Pascal)。
输入
输入包含多组测试数据
货币系统中货币的种类数目是 V 。 (1<= V<=25)
要构造的数量钱是 N 。 (1<= N<=10,000)
第 1 行: 二整数， V 和 N
第 2 ..V+1行： 可用的货币 V 个整数　(每行一个　每行没有其它的数)。
输出
单独的一行包含那个可能的构造的方案数。
样例输入
3 10
1 2 5
样例输出
10
程序

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
int DP[26][10001];
//DP[i][v]=DP[i-1][v]+DP[i][v-w[i]]
//DP[0][v]=0;
//DP[i][0]=1;
int w[26];
int V,N;

int main(){
	while(cin>>V>>N){
		memset(DP,0,sizeof(DP));
		memset(w,0,sizeof(w));
		for(int i=1;i<=V;i++){
			cin>>w[i];
			DP[i][0]=1;
		}

		for(int i=1;i<=V;i++){
			for(int v=1;v<=N;v++){
				if(v<w[i]) DP[i][v]=DP[i-1][v];
				else DP[i][v]=DP[i-1][v]+DP[i][v-w[i]];
			}
		}
		cout<<DP[V][N]<<endl;
	}
	return 0;
}

图的遍历

图的深度优先搜索DFS

邻接矩阵

const int MAXV=1000;
const int INF=0x3f3f3f3f;
int n,G[MAXV][MAXV];
bool vis[MAXV]={false};

void DFSTravese(){
	for(int u=0;u<n;u++){
		if(!vis[u]){
			DFS(u);
		}
	}
}

void DFS(int u){
	vis[u]=true;
	for(int v=0;v<n;v++){
		if(!vis[v]&&G[u][v]!=INF){
			DFS(v);
		}
	}
}

邻接表

const int MAXV=1000;
const int INF=0x3f3f3f3f;
bool vis[MAXV]={false};
vector<int> G[MAXV];

void DFSTravese(){
  for(int u=0;u<n;u++){
    if(!vis[u]){
      DFS(u);
    }
  }
}

void DFS(int u){
  vis[u]=true;
  for(int i=0;i<G[u].size();i++){
    int v=G[u][i];
    if(!vis[v]){
      DFS(v);
    }
  }
}

PAT1034 Head of a Gang

Description
One way that the police finds the head of a gang is to check people’s phone calls. If there is a phone call between A and B, we say that A and B is related. The weight of a relation is defined to be the total time length of all the phone calls made between the two persons. A “Gang” is a cluster of more than 2 persons who are related to each other with total relation weight being greater than a given threthold K. In each gang, the one with maximum total weight is the head. Now given a list of phone calls, you are supposed to find the gangs and the heads.
Input Specification
Each input file contains one test case. For each case, the first line contains two positive numbers N and K (both less than or equal to 1000), the number of phone calls and the weight threthold, respectively. Then N lines follow, each in the following format:
Name1 Name2 Time
where Name1 and Name2 are the names of people at the two ends of the call, and Time is the length of the call. A name is a string of three capital letters chosen from A-Z. A time length is a positive integer which is no more than 1000 minutes.
Output Specification
For each test case, first print in a line the total number of gangs. Then for each gang, print in a line the name of the head and the total number of the members. It is guaranteed that the head is unique for each gang. The output must be sorted according to the alphabetical order of the names of the heads.
Sample Input 1
8 59
AAA BBB 10
BBB AAA 20
AAA CCC 40
DDD EEE 5
EEE DDD 70
FFF GGG 30
GGG HHH 20
HHH FFF 10
Sample Output 1
2
AAA 3
GGG 3
Sample Input 2
8 70
AAA BBB 10
BBB AAA 20
AAA CCC 40
DDD EEE 5
EEE DDD 70
FFF GGG 30
GGG HHH 20
HHH FFF 10
Sample Output 2
0
Procedure

#include<iostream>
#include<map>
#include<cstring>
using namespace std;

const int MAXV=2001;
const int INF=0x3f3f3f3f;

int G[MAXV][MAXV];
bool vis[MAXV];
int weight[MAXV];

map<string,int> stringToInt;//姓名->编号
map<int,string> intToString;//编号->姓名
map<string,int> gangs;//Head，人数
int numPersons;
int N,K;
void DFS(int u,int &head,int &totalWeight,int &members){
	vis[u]=true;
	members++;
	if(weight[u]>weight[head]){
		head=u;
	}
	for(int v=0;v<numPersons;v++){
//ERROR:注意环！如果先判断vis则导致有边权未统计
//		if(!vis[v]&&G[u][v]!=0){
//			totalWeight+=G[u][v];
//			DFS(v,head,totalWeight,members);
//		}
		if(G[u][v]!=0){
			totalWeight+=G[u][v];
			G[u][v]=G[v][u]=0;
			if(!vis[v]){
				DFS(v,head,totalWeight,members);
			}
		}
	}
}
void DFSTraverse(){
	for(int u=0;u<numPersons;u++){
		if(!vis[u]){
			int head=u;
			int totalWeight=0;
			int members=0;
			DFS(u,head,totalWeight,members);
			if(members>2&&totalWeight>K){
				gangs[intToString[head]]=members;
			}
		}
	}
}
//获取编号
int getNumber(string str){
	if(stringToInt.find(str)!=stringToInt.end()){
		return stringToInt[str];
	}else{
		stringToInt[str]=numPersons;
		intToString[numPersons]=str;
		return numPersons++;
	}
}
int main(){
	while(cin>>N>>K){
		//初始化
		numPersons=0;
		gangs.clear();
		intToString.clear();
		stringToInt.clear();
		memset(vis,false,sizeof(vis));
		memset(weight,0,sizeof(weight));
		memset(G,0,sizeof(G));
		//输入
		string name1,name2;
		int w;
		for(int i=0;i<N;i++){
			cin>>name1>>name2>>w;
			int num1=getNumber(name1);
			int num2=getNumber(name2);
			weight[num1]+=w;
			weight[num2]+=w;
			G[num1][num2]+=w; //重复边
			G[num2][num1]+=w;
		}
		//运算
		DFSTraverse();
		//输出
		cout<<gangs.size()<<endl;
		for(map<string,int>::iterator it=gangs.begin();it!=gangs.end();it++){
			cout<<it->first<<" "<<it->second<<endl;
		}
	}
	return 0;
}

第一题

题目描述
该题的目的是要你统计图的连通分支数。
输入
每个输入文件包含若干行，每行两个整数i,j，表示节点i和j之间存在一条边。
输出
输出每个图的联通分支数。
样例输入
1 4
4 3
5 5
样例输出
2
程序

#include<iostream>
#include<cstring>
#include<map>
#include<vector>
using namespace std;
const int MAXV=1000001;
int u,v;
vector<int> Adj[MAXV];
bool bVisited[MAXV];
bool bExist[MAXV];

void DFS(int u){
	bVisited[u]=true;
	for(int i=0;i<Adj[u].size();i++){
		int v=Adj[u][i];
		if(!bVisited[v]){
			DFS(v);
		}
	}
}
int DFSTraverse(){
	int numBranches=0;
	for(int i=1;i<MAXV;i++){
		if(!bVisited[i]&&bExist[i]){
			DFS(i);
			numBranches++;
		}
	}
	return numBranches;
}
int main(){

	memset(bVisited,false,sizeof(bVisited));
	memset(bExist,false,sizeof(bExist));
	while(cin>>u>>v){
		bExist[u]=true;
		bExist[v]=true;
		Adj[u].push_back(v);
		Adj[v].push_back(u);
	}
	cout<<DFSTraverse()<<endl;
	return 0;
}

连通图

题目描述
给定一个无向图和其中的所有边，判断这个图是否所有顶点都是连通的。
输入
每组数据的第一行是两个整数 n 和 m（0<=n<=1000）。n 表示图的顶点数目，m 表示图中边的数目。如果 n 为 0 表示输入结束。随后有 m 行数据，每行有两个值 x 和 y（0<x, y <=n），表示顶点 x 和 y 相连，顶点的编号从 1 开始计算。输入不保证这些边是否重复。
输出
对于每组输入数据，如果所有顶点都是连通的，输出”YES”，否则输出”NO”。
样例输入
4 3
4 3
1 2
1 3
5 7
3 5
2 3
1 3
3 2
2 5
3 4
4 1
7 3
6 2
3 1
5 6
0 0
样例输出
YES
YES
NO
程序

#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
const int MAXV=1001;
int n,m;
int G[MAXV][MAXV];
bool bVis[MAXV];
int num;
void DFS(int u){
	bVis[u]=true;
	num++;
	for(int i=1;i<=n;i++){
		if(!bVis[i]&&G[u][i]!=0){
			DFS(i);
		}
	}
}
bool DFSTraverse(){
	num=0;
	DFS(1);
	if(num!=n) return false;
	else return true;
}
int main(){
	while(cin>>n>>m&&n!=0){
		int x,y;
		memset(G,0,sizeof(G));
		memset(bVis,false,sizeof(bVis));
		for(int i=0;i<m;i++){
			cin>>x>>y;
			G[x][y]=G[y][x]=1;
		}
		if(DFSTraverse()) cout<<"YES"<<endl;
		else cout<<"NO"<<endl;
	}
	return 0;
}

#include<iostream>
using namespace std;
const int MAXV=1001;
int father[MAXV];

int n,m;
int findFather(int i){
	if(i!=father[i]){
		father[i]=findFather(father[i]);
	}
	return father[i];
}
void makeSet(){
	for(int i=0;i<MAXV;i++){
		father[i]=i;
	}
}
void unionSet(int x,int y){
	int fa=findFather(x);
	int fb=findFather(y);
	if(fa!=fb){
		father[fb]=fa;
		n--;
	}
}
int main(){
	while(cin>>n>>m&&n!=0){
		int x,y;
		makeSet();
		for(int i=0;i<m;i++){
			cin>>x>>y;
			unionSet(x,y);
		}
		if(n==1) cout<<"YES"<<endl;
		else cout<<"NO"<<endl;
	}
	return 0;
}

图的广度优先搜索

邻接矩阵

const int MAXV=101;
int n,G[MAXV][MAXV];
bool bInq[MAXV]={false};
void BFS(int u){
  bInq[u]=true;
  queue<ine> q;
  q.push(u);
  while(!q.empty()){
    int u=q.front();
    q.pop();
    for(int v=0;v<n;v++){
      if(!bInq[v]&&G[u][v]!=INF){
        q.push(v);
        bInq[v]=true;
      }
    }
  }
}

void BFSTraverse(){
  for(int u=0;u<n;u++){
    if(!bInq[u]){
      BFS(u);
    }
  }
}

邻接表

const int MAXV=101;
vector<int> Adj[MAXV];
int n;
bool bInq[MAXV]={false};
void BFS(int u){
  bInq[u]=true;
  queue<int> q;
  q.push(u);
  while(!q.empty()){
    int u=q.front();
    q.pop();
    for(int i=0;i<Adj[u].size();i++){
      int v=Adj[u][i];
      if(!bInq[v]){
        q.push(v);
        bInq[v]=true;
      }
    }
  }
}
void BFSTraverse(){
  for(int u=0;u<n;u++){
    if(!bInq[u]){
        BFS(u);
    }
  }
}

PAT-A1076 Forwards on Weibo

Description
Weibo is known as the Chinese version of Twitter. One user on Weibo may have many followers, and may follow many other users as well. Hence a social network is formed with followers relations. When a user makes a post on Weibo, all his/her followers can view and forward his/her post, which can then be forwarded again by their followers. Now given a social network, you are supposed to calculate the maximum potential amount of forwards for any specific user, assuming that only L levels of indirect followers are counted.
Input Specification
Each input file contains one test case. For each case, the first line contains 2 positive integers: N (≤1000), the number of users; and L (≤6), the number of levels of indirect followers that are counted. Hence it is assumed that all the users are numbered from 1 to N. Then N lines follow, each in the format:
M[i] user_list[i]
where M[i] (≤100) is the total number of people that user[i] follows; and user_list[i] is a list of the M[i] users that followed by user[i]. It is guaranteed that no one can follow oneself. All the numbers are separated by a space.
Then finally a positive K is given, followed by K UserID’s for query.
Output Specification
For each UserID, you are supposed to print in one line the maximum potential amount of forwards this user can trigger, assuming that everyone who can view the initial post will forward it once, and that only L levels of indirect followers are counted.
Sample Input
7 3
3 2 3 4
0
2 5 6
2 3 1
2 3 4
1 4
1 5
2 2 6
Sample Output
4
5
Procedure

#include<iostream>
#include<queue>
#include<vector>
#include<cstring>
using namespace std;

const int MAXV=1001;
struct Node{
	int vertex;
	int layer;
	Node(){}
	Node(int v,int l):vertex(v),layer(l){}
};

int N,L;
vector<Node> Adj[MAXV];
bool bInq[MAXV];
int BFS(int u){
	memset(bInq,false,sizeof(bInq));
	queue<Node> q;
	bInq[u]=true;
	q.push(Node(u,0));
	int num=0;
	while(!q.empty()){
		Node tmp=q.front();
		q.pop();
		int u=tmp.vertex;
		for(int i=0;i<Adj[u].size();i++){
			Node v=Adj[u][i];
			v.layer=tmp.layer+1;
			if(!bInq[v.vertex]&&v.layer<=L){
				num++;
				q.push(v);
				bInq[v.vertex]=true;
			}
		}
	}
	return num;
}
int main(){
	cin>>N>>L;
	for(int i=1;i<=N;i++){
		int m;
		cin>>m;
		for(int j=0;j<m;j++){
			int v;
			cin>>v;
			Adj[v].push_back(Node(i,1));
		}
	}
	int m;
	cin>>m;
	for(int j=0;j<m;j++){
		int v;
		cin>>v;
		cout<<BFS(v)<<endl;
	}
	return 0;
}

最短路径

Dijkstra算法

邻接矩阵 O(V^{2})

适用于V不超过1000

const int MAXV=1001;
const int INF=0x3f3f3f3f;
int n,G[MAXV][MAXV];
bool bVis[MAXV];
int dist[MAXV];
void Dijkstra(int s){
  fill(dist,dist+MAXV,INF);
  fill(bVis,bVis+MAXV,false);
  dist[s]=0;
  for(int i=0;i<n;i++){
    int u=-1,MIN=INF;
    for(int j=0;j<n;j++){
      if(!bVis[j]&&dist[j]<MIN){
        u=j;
        MIN=dist[j];
      }
    }
    if(u==-1) return; //源点不连通
    bVis[u]=true;
    for(int v=0;v<n;v++){
      if(!bVis[v]&&G[u][v]!=INF&&dist[u]+G[u][v]<dist[v]){
        dist[v]=dist[u]+G[u][v];
      }
    }
  }
}

邻接表 O(V^{2}+E)

struct Node{
  int v;
  int dis;
}
vector<Node>　Adj[MAXV];
int n;
int dist[MAXV];
bool bVis[MAXV];

void Dijkstra(int s){
  fill(dist,dist+MAXV,INF);
  fill(bVis,bVis+MAXV,false);
  dist[s]=0;
  for(int i=0;i<n;i++){
    int u=-s,MIN=INF;
    for(int j=0;j<n;j++){
      if(!bVis[j]&&dist[j]<MIN){
        u=j;
        MIN=dist[j];
      }
    }
    if(u==-1) return;
    for(int k=0;k<Adj[u].size();k++){
      int v=Adj[u][k].v;
      if(!bVis[v]&&Adj[u][k].dis+MIN<dist[v]){
        dist[v]=Adj[u][k].dis+MIN;
      }
    }
  }
}

堆优化 O(VlogV+E)

const int INF=0x3f3f3f3f;
const int MAXV=1001;
struct Node{
  int v;
  int dis;
  Node(){}
  Node(int vv,int dd):v(vv),dis(dd){}
  bool operator < (const Node& tmp) const{
    return dis<tmp.dist;
  }
}；
vector<Node> Adj[MAXV];
int dist[MAXV];
int bVis[MAXV];
void Dijstra_mini(int s){
  fill(bVis,bVis+MAXV,false);
  fill(dist,dist+MAXV,INF);
  priority_queue<Node> pq;
  dist[s]=0;
  pq.push(Node(s,0));
  int nDone=1;
  while(nDone<n&&!pq.empty()){
    Node top=pq.top();
    pq.pop();
    if(!bVis[top.v]){
      nDone++;
        bVis[top.v]=true;
    }else{
      continue;
    }

    for(int i=0;i<Adj[top.v].size();i++){
      int  v=Adj[top.v][i];
      int dis=Adj[top.v][i].dis;
      if(!bVist[v]&&dis+top.dis<dist[v]){
        dist[v]=dis+top.dis;
        pq.push(Node(v,dist[v]));
      }
    }
  }
}

变形

新增边权（比如花费）求最短路径下的花费最小

for(int v=0;v<n;v++){
  if(!bVis[v]&&G[u][v]!=INF){
    if(dist[u]+G[u][v]<dist[v]){
      dist[v]=dist[u]+G[u][v];
      c[v]=c[u]+cost[u][v];
    }else if(dist[u]+G[u][v]==dist[v]&&c[u]+cost[u][v]<c[v]){
      c[v]=c[u]+cost[u][v];
    }
  }
}

新增点权（比如物资）求最短路径下的收集的物资最大

for(int v=0;v<n;v++){
  if(!bVis[v]&&G[u][v]!=INF){
    if(dist[u]+G[u][v]<dist[v]){
      dis[v]=dist[u]+G[u][v];
      w[v]=w[u]+weight[v];
    }else if(dist[u]+G[u][v]==dist[v]&&w[u]+weight[v]>w[v]){
      w[v]=w[u]+weight[v];
    }
  }

求最短路径条数

for(int v=0;v<n;v++){
  if(!bVis[u]&&G[u][v]!=INF){
    if(dist[u]+G[u][v]<dist[v]){
      dist[v]=dist[u]+G[u][v];
      num[v]=num[u];
    }else if(dist[u]+G[u][v]==dist[v]){
      num[v]+=num[u];
    }
  }
}

求路径

...
for(int i=0;i<n;i++) pre[i]=i;
...
for(int v=0;v<n;v++){
  if(!bVis[v]&&G[u][v]!=INF&&dist[u]+G[u][v]<dist[v]){
    dist[v]=dist[u]+G[u][v];
    pre[v]=u;
  }
}

//递归打路径
void DFS(int s,int v){
  if(s==v){
    std::cout<<s<<endl;
    return;
  }
  DFS(s,pre[v]);
  std::cout<<v<<endl;
}

Dijkstra+DFS

上述几种变形都满足贪心的最优子结构，但实际情况可能出现一些逻辑更复杂的计算边权或点权的方式，上述方法就不一定能够算出正确的结果
故介绍一种更加通用、又模板化的解决方法：
现在Dijkstra算法中记录所有最短路径，然后从这些最短路径中选出一条满足第二标尺的路径！
不妨把pre数组定义为vector pre[MAXV];，这样对每个节点v来说，pre[v]就是一个边长的数组vetor，里面用来存放点v的所有能产生最短路径的前驱节点。
那么，在原有Dijkstra算法基础上更改代码即可：

if(dist[u]+G[u][v]<dist[v]){
  dist[v]=dist[u]+G[u][v];
  pre[v].clear();
  pre[v].push_back(u);
}else if(dist[u]+G[u][v]==dist[v]){
  pre[v].push_back(u);
}

PAT-A1003 Emergency（25）

As an emergency rescue team leader of a city, you are given a special map of your country. The map shows several scattered cities connected by some roads. Amount of rescue teams in each city and the length of each road between any pair of cities are marked on the map. When there is an emergency call to you from some other city, your job is to lead your men to the place as quickly as possible, and at the mean time, call up as many hands on the way as possible.
Input Specification
Each input file contains one test case. For each test case, the first line contains 4 positive integers: N (≤500) - the number of cities (and the cities are numbered from 0 to N−1), M - the number of roads, C1 and C2 - the cities that you are currently in and that you must save, respectively. The next line contains N integers, where the i-th integer is the number of rescue teams in the i-th city. Then M lines follow, each describes a road with three integers c1
​​ , c2 and L, which are the pair of cities connected by a road and the length of that road, respectively. It is guaranteed that there exists at least one path from C1 to C2.
Output Specification
For each test case, print in one line two numbers: the number of different shortest paths between C1 and C2, and the maximum amount of rescue teams you can possibly gather. All the numbers in a line must be separated by exactly one space, and there is no extra space allowed at the end of a line.
Sample Input
5 6 0 2
1 2 1 5 3
0 1 1
0 2 2
0 3 1
1 2 1
2 4 1
3 4 1
Sample Output
2 4
Procedure

//邻接矩阵
#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
const int MAXV=501;
const int INF=0x3f3f3f3f;
int n,m,s,e;
int G[MAXV][MAXV];
bool bVis[MAXV];
int dist[MAXV];
int num[MAXV];
int weight[MAXV];
int w[MAXV];
void Dijkstra(int s){
	memset(dist,INF,sizeof(dist));
	memset(bVis,false,sizeof(bVis));
	memset(num,0,sizeof(num));
	memset(w,0,sizeof(w));
	w[s]=weight[s];
	num[s]=1;
	dist[s]=0;
	for(int i=0;i<n;i++){
		int u=-1,MIN=INF;
		for(int j=0;j<n;j++){
			if(!bVis[j]&&dist[j]<MIN){
				u=j;
				MIN=dist[j];
			}
		}
		if(u==-1) return;
		bVis[u]=true;
		for(int v=0;v<n;v++){
			if(!bVis[v]&&G[u][v]!=INF){
				if(dist[u]+G[u][v]<dist[v]){
					dist[v]=dist[u]+G[u][v];
					w[v]=w[u]+weight[v];
					num[v]=num[u];
				}else if(dist[u]+G[u][v]==dist[v]){
					num[v]+=num[u];
					if(w[u]+weight[v]>w[v]){
						w[v]=w[u]+weight[v];
					}
				}
			}
		}
	}
}
int main(){
	cin>>n>>m>>s>>e;
	for(int i=0;i<n;i++){
		cin>>weight[i];
	}
	memset(G,INF,sizeof(G));
	for(int i=0;i<m;i++){
		int s,e,l;
		cin>>s>>e>>l;
		G[s][e]=G[e][s]=l;
	}
	Dijkstra(s);
	cout<<num[e]<<" "<<w[e]<<endl;
	return 0;
}

//邻接表
#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
const int MAXV=501;
const int INF=0x3f3f3f3f;
int n,m,s,e;
struct Node{
	int v;
	int dis;
	Node(){}
	Node(int vv,int dd):v(vv),dis(dd){}
};
int dist[MAXV];
bool bVis[MAXV];
int num[MAXV];
int weight[MAXV];
int w[MAXV];
vector<Node> Adj[MAXV];
void Dijkstra(int s){
	memset(dist,INF,sizeof(dist));
	memset(bVis,false,sizeof(bVis));
	memset(num,0,sizeof(num));
	memset(w,0,sizeof(w));
	num[s]=1;
	w[s]=weight[s];
	dist[s]=0;
	for(int i=0;i<n;i++){
		int u=-1,MIN=INF;
		for(int j=0;j<n;j++){
			if(!bVis[j]&&dist[j]<MIN){
				u=j;
				MIN=dist[j];
			}
		}
		if(u==-1) return;
		bVis[u]=true;
		for(int j=0;j<Adj[u].size();j++){
			int v=Adj[u][j].v;
			int dis=Adj[u][j].dis;
			if(!bVis[v]){
				if(dist[u]+dis<dist[v]){
					dist[v]=dist[u]+dis;
					w[v]=w[u]+weight[v];
					num[v]=num[u];
				}else if(dist[u]+dis==dist[v]){
					num[v]+=num[u];
					if(w[u]+weight[v]>w[v]){
						w[v]=w[u]+weight[v];
					}
				}
			}
		}
	}
}
int main(){
	cin>>n>>m>>s>>e;
	for(int i=0;i<n;i++){
		cin>>weight[i];
	}
	for(int i=0;i<m;i++){
		int s,e,l;
		cin>>s>>e>>l;
		Adj[s].push_back(Node(e,l));
		Adj[e].push_back(Node(s,l));
	}
	Dijkstra(s);
	cout<<num[e]<<" "<<w[e]<<endl;
	return 0;
}

//邻接表+堆
#include<iostream>
#include<vector>
#include<cstring>
#include<queue>
using namespace std;
const int MAXV=501;
const int INF=0X3f3f3f3f;
int n,m,s,e;
struct Node{
	int v;
	int dis;
	Node(){}
	Node(int vv,int dd):v(vv),dis(dd){}
	bool operator < (const Node& tmp) const{
		return dis>tmp.dis;
	}
};
vector<Node> Adj[MAXV];
int num[MAXV];
int weight[MAXV];
int w[MAXV];
int dist[MAXV];
bool bVis[MAXV];
void Dijkstra(int s){
	memset(num,0,sizeof(num));
	memset(w,0,sizeof(w));
	memset(dist,INF,sizeof(dist));
	memset(bVis,false,sizeof(bVis));
	num[s]=1;
	w[s]=weight[s];
	dist[s]=0;
	priority_queue<Node> pq;
	pq.push(Node(s,0));
	int iChecked=0;
	while(!pq.empty()&&iChecked<n){
		Node top=pq.top();
		pq.pop();
		bVis[top.v]=true;
		iChecked++;
		for(int i=0;i<Adj[top.v].size();i++){
			int v=Adj[top.v][i].v;
			int dis=Adj[top.v][i].dis;
			if(!bVis[v]){
				if(dis+dist[top.v]<dist[v]){
					dist[v]=dis+dist[top.v];
					num[v]=num[top.v];
					w[v]=w[top.v]+weight[v];
					pq.push(Node(v,dist[v]));
				}else if(dis+dist[top.v]==dist[v]){
					num[v]+=num[top.v];
					if(w[top.v]+weight[v]>w[v]){
						w[v]=w[top.v]+weight[v];
					}
				}
			}
		}
	}
}
int main(){
	cin>>n>>m>>s>>e;
	for(int i=0;i<n;i++){
		cin>>weight[i];
	}
	for(int i=0;i<m;i++){
		int s,e,l;
		cin>>s>>e>>l;
		Adj[s].push_back(Node(e,l));
		Adj[e].push_back(Node(s,l));
	}
	Dijkstra(s);
	cout<<num[e]<<" "<<w[e]<<endl;
	return 0;
}

1030 Travel Plan (30)

A traveler’s map gives the distances between cities along the highways, together with the cost of each highway. Now you are supposed to write a program to help a traveler to decide the shortest path between his/her starting city and the destination. If such a shortest path is not unique, you are supposed to output the one with the minimum cost, which is guaranteed to be unique.
Input Specification
Each input file contains one test case. Each case starts with a line containing 4 positive integers N, M, S, and D, where N (≤500) is the number of cities (and hence the cities are numbered from 0 to N−1); M is the number of highways; S and D are the starting and the destination cities, respectively. Then M lines follow, each provides the information of a highway, in the format:
City1 City2 Distance Cost
where the numbers are all integers no more than 500, and are separated by a space.
Output Specification
For each test case, print in one line the cities along the shortest path from the starting point to the destination, followed by the total distance and the total cost of the path. The numbers must be separated by a space and there must be no extra space at the end of output.
Sample Input
4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20
Sample Output
0 2 3 3 40
Procedure

//Dijkstra+堆
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int MAXV=501;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int dis;
	int cost;
	Node(){}
	Node(int vv,int dd,int cc):v(vv),dis(dd),cost(cc){}
	bool operator < (const Node& tmp) const{
		if(dis!=tmp.dis){
			return dis>tmp.dis;
		}else{
			return cost>tmp.cost;
		}
	}
};
vector<Node> Adj[MAXV];
int pre[MAXV];
int dist[MAXV];
bool bVis[MAXV];
int cost[MAXV];
int n,m,s,d;

void print(int v){
	if(v==s){
		cout<<s;
		return;
	}
	print(pre[v]);
	cout<<" "<<v;
}
void Dijkstra(int s){
	memset(dist,INF,sizeof(dist));
	memset(bVis,false,sizeof(bVis));
	memset(cost,INF,sizeof(cost));
	for(int i=0;i<n;i++) pre[i]=i;
	dist[s]=0;
	cost[s]=0;
	priority_queue<Node> pq;
	pq.push(Node(s,0,0));
	int nChecked=0;
	while(!pq.empty()&&nChecked<n){
		Node top=pq.top();
		pq.pop();
		bVis[top.v]=true;
		for(unsigned int i=0;i<Adj[top.v].size();i++){
			int v=Adj[top.v][i].v;
			int dis=Adj[top.v][i].dis;
			int cos=Adj[top.v][i].cost;
			if(!bVis[v]){
				if(dist[top.v]+dis<dist[v]){
					dist[v]=dist[top.v]+dis;
					pre[v]=top.v;
					cost[v]=cost[top.v]+cos;
					pq.push(Node(v,dist[v],cost[v]));
				}else if(dist[top.v]+dis==dist[v]){
					if(cost[top.v]+cos<cost[v]){
						pre[v]=top.v;
						cost[v]=cost[top.v]+cos;
						pq.push(Node(v,dist[v],cost[v]));
					}
				}
			}
		}
	}
}
int main(){
	cin>>n>>m>>s>>d;
	for(int i=0;i<m;i++){
		int u,v,dis,cos;
		cin>>u>>v>>dis>>cos;
		Adj[u].push_back(Node(v,dis,cos));
		Adj[v].push_back(Node(u,dis,cos));
	}
	Dijkstra(s);
	print(d);
	cout<<" "<<dist[d]<<" "<<cost[d]<<endl;
	return 0;
}

//Dijkstra+DFS
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int MAXV=501;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int dis;
	int cos;
	Node(){}
	Node(int vv,int dd,int cc):v(vv),dis(dd),cos(cc){}
	bool operator < (const Node& tmp) const{
		return dis>tmp.dis;

	}
};
vector<Node> Adj[MAXV];
vector<int> pre[MAXV];
int bVis[MAXV];
int dist[MAXV];
int optCost=INF;
int n,m,s,d;

vector<int> path,tmpPath;
int findUV(int u,int v){
	for(int i=0;i<Adj[u].size();i++){
		if(Adj[u][i].v==v){
			return Adj[u][i].cos;
		}
	}
	return 0;
}
void DFS(int v){
	if(v==s){
		tmpPath.push_back(v);
		int tmpCost=0;
		for(int i=tmpPath.size()-1;i>0;i--){
			int u=tmpPath[i],v=tmpPath[i-1];
			tmpCost+=findUV(u,v);
		}
		if(tmpCost<optCost){
			optCost=tmpCost;
			path=tmpPath;
		}
		tmpPath.pop_back();
		return;
	}
	tmpPath.push_back(v);
	for(int i=0;i<pre[v].size();i++){
		DFS(pre[v][i]);
	}
	tmpPath.pop_back();
}
void Dijkstra(int s){
	memset(bVis,false,sizeof(bVis));
	memset(dist,INF,sizeof(dist));
	dist[s]=0;
	priority_queue<Node> pq;
	pq.push(Node(s,0,0));
	int nChecked=0;
	while(!pq.empty()&&nChecked<n){
		Node top=pq.top();
		pq.pop();
		bVis[top.v]=true;
		for(int i=0;i<Adj[top.v].size();i++){
			int v=Adj[top.v][i].v;
			int dis=Adj[top.v][i].dis;
			if(!bVis[v]){
				if(dist[top.v]+dis<dist[v]){
					dist[v]=dist[top.v]+dis;
					pre[v].clear();
					pre[v].push_back(top.v);
					pq.push(Node(v,dist[v],0));
				}else if(dist[top.v]+dis==dist[v]){
					pre[v].push_back(top.v);
				}
			}
		}
	}
}
int main(){
	cin>>n>>m>>s>>d;
	for(int i=0;i<m;i++){
		int s,e,d,c;
		cin>>s>>e>>d>>c;
		Adj[s].push_back(Node(e,d,c));
		Adj[e].push_back(Node(s,d,c));
	}
	Dijkstra(s);
	DFS(d);
	for(int i=path.size()-1;i>=0;i--){
		cout<<path[i]<<" ";
	}
	cout<<dist[d]<<" "<<optCost<<endl;
	return 0;
}

Bellman-Ford算法 O(VE)

const int MAXV=1000;
const int INF=0x3f3f3f3f;
struct Node{
  int v;
  int dis;
}
vector<Node> Adj[MAXV];
int n;
int dist[MAXV];

bool Bellman(int s){
  memset(dist,INF,sizeof(dist));
  dist[s]=0;
  bool bChange=false;
  for(int i=0;i<n-1;i++){
    for(int u=0;u<n;u++){
      for(int j=0;j<Adj[u].size();j++){
        int v=Adj[u][j].v;
        int dis=Adj[u][j].dis;
        if(dist[u]+dis<dist[v]){
          dist[v]=dist[u]+dis;
          bChange=true;
        }
      }
    }
    if(!bChange) return true;
  }

  for(int u=0;u<n;u++){
    for(int j=0;j<Adj[u].size();j++){
      int v=Adj[u][j].v;
      int dis=Adj[u][j].dis;
      if(dist[u]+dis<dist[v]){
        return false;
      }
    }
  }
  return true;
}

PAT-A1003 Emergency（25）

As an emergency rescue team leader of a city, you are given a special map of your country. The map shows several scattered cities connected by some roads. Amount of rescue teams in each city and the length of each road between any pair of cities are marked on the map. When there is an emergency call to you from some other city, your job is to lead your men to the place as quickly as possible, and at the mean time, call up as many hands on the way as possible.
Input Specification
Each input file contains one test case. For each test case, the first line contains 4 positive integers: N (≤500) - the number of cities (and the cities are numbered from 0 to N−1), M - the number of roads, C1 and C2 - the cities that you are currently in and that you must save, respectively. The next line contains N integers, where the i-th integer is the number of rescue teams in the i-th city. Then M lines follow, each describes a road with three integers c1
​​ , c2 and L, which are the pair of cities connected by a road and the length of that road, respectively. It is guaranteed that there exists at least one path from C1 to C2.
Output Specification
For each test case, print in one line two numbers: the number of different shortest paths between C1 and C2, and the maximum amount of rescue teams you can possibly gather. All the numbers in a line must be separated by exactly one space, and there is no extra space allowed at the end of a line.
Sample Input
5 6 0 2
1 2 1 5 3
0 1 1
0 2 2
0 3 1
1 2 1
2 4 1
3 4 1
Sample Output
2 4
Procedure

#include<iostream>
#include<vector>
#include<cstring>
#include<algorithm>
#include<set>
using namespace std;
const int MAXV=501;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int dis;
	Node(){}
	Node(int vv,int dd):v(vv),dis(dd){}
};
vector<Node> Adj[MAXV];
int num[MAXV];
set<int> pre[MAXV];
int dist[MAXV];
int weight[MAXV];
int w[MAXV];
int N,M,s,e;

void Bellman_Ford(int s){
	memset(num,0,sizeof(num));
	memset(dist,INF,sizeof(dist));
	memset(w,INF,sizeof(w));
	w[s]=weight[s];
	dist[s]=0;
	num[s]=1;
	bool bChange=false;
	for(int i=0;i<N-1;i++){
		for(int u=0;u<N;u++){
			for(int j=0;j<Adj[u].size();j++){
				int v=Adj[u][j].v;
				int dis=Adj[u][j].dis;
				if(dist[u]+dis<dist[v]){
					dist[v]=dist[u]+dis;
					num[v]=num[u];
					w[v]=w[u]+weight[v];
					pre[v].clear();
					pre[v].insert(u);
					bChange=true;
				}else if(dist[u]+dis==dist[v]){
					if(w[u]+weight[v]>w[v]){
						w[v]=w[u]+weight[v];
					}
					pre[v].insert(u);
					num[v]=0;
					for(set<int>::iterator it=pre[v].begin();it!=pre[v].end();it++){
						num[v]+=num[*it];
					}
				}
			}
		}
		if(!bChange) return;
	}
}
int main(){
	cin>>N>>M>>s>>e;
	for(int i=0;i<N;i++) cin>>weight[i];
	for(int i=0;i<M;i++){
		int s,e,l;
		cin>>s>>e>>l;
		Adj[s].push_back(Node(e,l));
		Adj[e].push_back(Node(s,l));
	}
	Bellman_Ford(s);
	cout<<num[e]<<" "<<w[e]<<endl;
	return 0;
}

SPFA算法 O(kE)

• 期望时间复杂度O(kE),多数情况下k不超过2，可见该算法大部分数据异常高效，并经常性地优于堆优化的Dijkstra算法。
  然而，如果存在负环则会退化到O(VE)
• SPFA算法可以判断是否存在从源点可达的负环，如果负环从源点不可达，则需要添加一个辅助顶点C，并添加一条从源点到达C的有向边以及V-1从C到达除源点外各顶点的有向边才能判断负环是否存在
• SPFA十分灵活，其内部的写法可以根据具体场景的不同进行调整：
  ①优先队列实现
  ②双端队列实现
  ③栈实现

vector<Node> Adj[MAXV];
int n,dist[MAXV],num[MAXV];
bool inq[MAXV];

bool SPFA(int s){
  memset(inq,false,sizeof(inq));
  memset(num,0,sizeof(num));
  fill(d,d+MAXV,INF);
  queue<int> Q;
  Q.push(s);
  while(!Q.empty()){
    int u=Q.front();
    Q.pop();
    inq[u]=false;
    for(int j=0;j<Adj[u].size();j++){
      int v=Adj[u][j].v;
      int dis=Adj[u][j].dis;
      if(dist[u]+dis<dist[v]){
        dist[v]=dist[u]+dis;
        if(!inq[v]){
          Q.push(v);
          intq[v]=true;
          num[v]++;  //v的入队次数
          if(num[v]>=n) return false; //有可达负环
        }
      }
    }
  }
  return true;
}

int num[MAXV];
struct Cmp{
	bool operator ()(const int &a, const int &b)const{
		return dist[a]>dist[b];
	}
};
bool SPFA(int s){
	memset(dist, INF, sizeof(dist));
	memset(num, 0, sizeof(num));
	memset(vis, false, sizeof(vis));
	dist[s]=0;
	priority_queue<int, vector<int>, Cmp> pq;
	pq.push(s);
	int nDone=0;
	while(nDone<n&&!pq.empty()){
		int u=pq.top();
		pq.pop();
		if(!vis[u]){
			vis[u]=true;
			nDone++;
		}else continue;
		for(int j=0;j<Adj[u].size();j++){
			int v=Adj[u][j].v;
			int dis=Adj[u][j].dis;
			if(!vis[v]&&dist[u]+dis<dist[v]){
				dist[v]=dist[u]+dis;
				num[v]++;
        pq.push(v);
				if(num[v]>=n) return false;
			}
		}
	}
	return true;
}

PAT-A1003 Emergency（25）

As an emergency rescue team leader of a city, you are given a special map of your country. The map shows several scattered cities connected by some roads. Amount of rescue teams in each city and the length of each road between any pair of cities are marked on the map. When there is an emergency call to you from some other city, your job is to lead your men to the place as quickly as possible, and at the mean time, call up as many hands on the way as possible.
Input Specification
Each input file contains one test case. For each test case, the first line contains 4 positive integers: N (≤500) - the number of cities (and the cities are numbered from 0 to N−1), M - the number of roads, C1 and C2 - the cities that you are currently in and that you must save, respectively. The next line contains N integers, where the i-th integer is the number of rescue teams in the i-th city. Then M lines follow, each describes a road with three integers c1
​​ , c2 and L, which are the pair of cities connected by a road and the length of that road, respectively. It is guaranteed that there exists at least one path from C1 to C2.
Output Specification
For each test case, print in one line two numbers: the number of different shortest paths between C1 and C2, and the maximum amount of rescue teams you can possibly gather. All the numbers in a line must be separated by exactly one space, and there is no extra space allowed at the end of a line.
Sample Input
5 6 0 2
1 2 1 5 3
0 1 1
0 2 2
0 3 1
1 2 1
2 4 1
3 4 1
Sample Output
2 4
Procedure

#include<iostream>
#include<vector>
#include<cstring>
#include<algorithm>
#include<queue>
#include<set>
using namespace std;
const int MAXV=501;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int dis;
	Node(){}
	Node(int vv,int dd):v(vv),dis(dd){}
};
vector<Node> Adj[MAXV];
set<int> pre[MAXV];
int num[MAXV];
int dist[MAXV];
int weight[MAXV];
int w[MAXV];
bool bInq[MAXV];
int N,M,s,e;

void SPFA(int s){
	memset(num,0,sizeof(num));
	memset(dist,INF,sizeof(dist));
	memset(w,INF,sizeof(w));
	memset(bInq,false,sizeof(bInq));
	w[s]=weight[s];
	num[s]=1;
	dist[s]=0;
	queue<int> Q;
	Q.push(s);
	bInq[s]=true;
	while(!Q.empty()){
	 	int u=Q.front();
	 	Q.pop();
	 	bInq[u]=false;
	 	for(int i=0;i<Adj[u].size();i++){
	 		int v=Adj[u][i].v;
	 		int dis=Adj[u][i].dis;
	 		if(dist[u]+dis<dist[v]){
	 			dist[v]=dist[u]+dis;
	 			w[v]=w[u]+weight[v];
	 			num[v]=num[u];
	 			pre[v].clear();
				pre[v].insert(u);
	 			if(!bInq[v]){
	 				Q.push(v);
					bInq[v]=true;
				}
			 }else if(dist[u]+dis==dist[v]){
			 	if(!bInq[v]){
	 				Q.push(v);
					bInq[v]=true;
				}
			 	num[v]=0;
			 	pre[v].insert(u);
			 	for(set<int>::iterator it=pre[v].begin();it!=pre[v].end();it++){
					num[v]+=num[*it]; 		
				}
				if(w[u]+weight[v]>w[v]){
					w[v]=w[u]+weight[v];
				}
			 }
		 }
	 }
}
int main(){
	cin>>N>>M>>s>>e;
	for(int i=0;i<N;i++) cin>>weight[i];
	for(int i=0;i<M;i++){
		int s,e,l;
		cin>>s>>e>>l;
		Adj[s].push_back(Node(e,l));
		Adj[e].push_back(Node(s,l));
	}
	SPFA(s);
	cout<<num[e]<<" "<<w[e]<<endl;
	return 0;
}

1030 Travel Plan (30)

A traveler’s map gives the distances between cities along the highways, together with the cost of each highway. Now you are supposed to write a program to help a traveler to decide the shortest path between his/her starting city and the destination. If such a shortest path is not unique, you are supposed to output the one with the minimum cost, which is guaranteed to be unique.
Input Specification
Each input file contains one test case. Each case starts with a line containing 4 positive integers N, M, S, and D, where N (≤500) is the number of cities (and hence the cities are numbered from 0 to N−1); M is the number of highways; S and D are the starting and the destination cities, respectively. Then M lines follow, each provides the information of a highway, in the format:
City1 City2 Distance Cost
where the numbers are all integers no more than 500, and are separated by a space.
Output Specification
For each test case, print in one line the cities along the shortest path from the starting point to the destination, followed by the total distance and the total cost of the path. The numbers must be separated by a space and there must be no extra space at the end of output.
Sample Input
4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20
Sample Output
0 2 3 3 40
Procedure

#include<iostream>
#include<vector>
#include<cstring>
#include<algorithm>
#include<queue>
#include<set>
using namespace std;
const int MAXV=501;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int dis;
	int cos;
	Node(){}
	Node(int vv,int dd,int cc):v(vv),dis(dd),cos(cc){}
};
vector<Node> Adj[MAXV];
int pre[MAXV];
int dist[MAXV];
int cost[MAXV];
bool bInq[MAXV];
int N,M,S,E;

void SPFA(int s){
	memset(cost,INF,sizeof(cost));
	memset(bInq,false,sizeof(bInq));
	memset(dist,INF,sizeof(dist));
	dist[s]=0;
	cost[s]=0;
	queue<int> Q;
	Q.push(s);
	bInq[s]=true;
	pre[s]=s;
	while(!Q.empty()){
		int u=Q.front();
		Q.pop();
		bInq[u]=false;
		for(int i=0;i<Adj[u].size();i++){
			int v=Adj[u][i].v;
			int dis=Adj[u][i].dis;
			int cos=Adj[u][i].cos;
			if(dist[u]+dis<dist[v]){
				dist[v]=dist[u]+dis;
				cost[v]=cost[u]+cos;
				pre[v]=u;
				if(!bInq[v]){
					Q.push(v);
					bInq[v]=true;
				}
			}else if(dist[u]+dis==dist[v]){
				if(!bInq[v]){
					Q.push(v);
					bInq[v]=true;
				}
				if(cost[u]+cos<cost[v]){
					cost[v]=cost[u]+cos;
					pre[v]=u;
				}
			}
		}
	}
}
void print(int e){
	if(pre[e]==e){
		cout<<e;
		return;
	}
	print(pre[e]);
	cout<<" "<<e;
}
int main(){
	cin>>N>>M>>S>>E;
	for(int i=0;i<M;i++){
		int s,e,d,c;
		cin>>s>>e>>d>>c;
		Adj[s].push_back(Node(e,d,c));
		Adj[e].push_back(Node(s,d,c));
	}
	SPFA(S);
	print(E);
	cout<<" "<<dist[E]<<" "<<cost[E]<<endl;
	return 0;
}

Floyd算法 $O(n^{3})$

解决全源最短路问题，即对给定的图G(V,E)，求任意两点u,v之间的最短路径长度，时间复杂度$O(n^{3})$。由于其复杂度决定了顶点数n限制约在200以内，因此使用邻接矩阵实现。

const int INF=0x3f3f3f3f;
const int MAXV=200;
int n,m;
int dis[MAXV][MAXV];

void Floyd(){
  for(int k=0;k<n;k++){
    for(int i=0;i<n;i++){
      for(int j=0;j<n;j++){
        if(dis[i][k]!=INF&&dis[k][j]!=INF&&dis[i][k]+dis[k][j]<dis[i][j]){
          dis[i][j]=dis[i][k]+dis[k][j];
        }
      }
    }
  }
}

int main(){
  int u,v,w;
  memset(dis,INF,sizeof(dis));
  cin>>n>>m;
  for(int i=0;i<n;i++){
    dis[i][i]=0;
  }
  for(int i=0;i<m;i++){
    cin>>u>>v>>w;
    dis[u][v]=w;
  }
  Floyd();
  for(int i=0;i<n;i++){
    for(int j=0;j<n;j++){
      cout<<dist[i][j]<<" ";
    }
    cout<<endl;
  }
  return 0;
}

练习

算法7-15：迪杰斯特拉最短路径算法

题目描述
在带权有向图G中，给定一个源点v，求从v到G中的其余各顶点的最短路径问题，叫做单源点的最短路径问题。
在常用的单源点最短路径算法中，迪杰斯特拉算法是最为常用的一种，是一种按照路径长度递增的次序产生最短路径的算法。
在本题中，读入一个有向图的带权邻接矩阵（即数组表示），建立有向图并按照以上描述中的算法求出源点至每一个其它顶点的最短路径长度。
输入
输入的第一行包含2个正整数n和s，表示图中共有n个顶点，且源点为s。其中n不超过50，s小于n。
以后的n行中每行有n个用空格隔开的整数。对于第i行的第j个整数，如果大于0，则表示第i个顶点有指向第j个顶点的有向边，且权值为对应的整数值；如果这个整数为0，则表示没有i指向j的有向边。当i和j相等的时候，保证对应的整数为0。
输出
只有一行，共有n-1个整数，表示源点至其它每一个顶点的最短路径长度。如果不存在从源点至相应顶点的路径，输出-1。
请注意行尾输出换行。
样例输入
4 1
0 3 0 1
0 0 4 0
2 0 0 0
0 0 1 0
样例输出
6 4 7
程序

#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
const int MAXV=51;
const int INF=0x3f3f3f3f;
int G[MAXV][MAXV];
bool bVis[MAXV];
int dist[MAXV];
int n,s;

bool cmp(int a,int b){
	return a>b;
}
void Dijkstra(int s){
	dist[s]=0;
	priority_queue<int> pq;
	pq.push(s);
	while(!pq.empty()){
		int u=pq.top();
		pq.pop();
		bVis[u]=true;
		for(int v=0;v<n;v++){
			if(G[u][v]!=0){
				if(dist[u]+G[u][v]<dist[v]){
					dist[v]=dist[u]+G[u][v];
					pq.push(v);
				}
			}
		}
	}
}
int main(){
	memset(G,0,sizeof(G));
	memset(bVis,false,sizeof(bVis));
	memset(dist,INF,sizeof(dist));
	cin>>n>>s;
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			cin>>G[i][j];
		}
	}
	Dijkstra(s);
	bool bFirst=true;
	for(int i=0;i<n;i++){
		if(i!=s){
			if(bFirst){
				bFirst=false;
			}else{
				cout<<" ";
			}
			if(dist[i]==INF) cout<<-1;
			else cout<<dist[i];
		}
	}
	cout<<endl;
	return 0;
}

算法7-16：弗洛伊德最短路径算法

题目描述
在带权有向图G中，求G中的任意一对顶点间的最短路径问题，也是十分常见的一种问题。
解决这个问题的一个方法是执行n次迪杰斯特拉算法，这样就可以求出每一对顶点间的最短路径，执行的时间复杂度为O(n3)。
而另一种算法是由弗洛伊德提出的，时间复杂度同样是O(n3)，但算法的形式简单很多。
在本题中，读入一个有向图的带权邻接矩阵（即数组表示），建立有向图并按照以上描述中的算法求出每一对顶点间的最短路径长度。
输入
输入的第一行包含1个正整数n，表示图中共有n个顶点。其中n不超过50。
以后的n行中每行有n个用空格隔开的整数。对于第i行的第j个整数，如果大于0，则表示第i个顶点有指向第j个顶点的有向边，且权值为对应的整数值；如果这个整数为0，则表示没有i指向j的有向边。当i和j相等的时候，保证对应的整数为0。
输出
共有n行，每行有n个整数，表示源点至每一个顶点的最短路径长度。如果不存在从源点至相应顶点的路径，输出-1。对于某个顶点到其本身的最短路径长度，输出0。
请在每个整数后输出一个空格，并请注意行尾输出换行。
样例输入
4
0 3 0 1
0 0 4 0
2 0 0 0
0 0 1 0
样例输出
0 3 2 1
6 0 4 7
2 5 0 3
3 6 1 0
程序

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int MAXV=51;
const int INF=0x3f3f3f3f;
int dist[MAXV][MAXV];
int n;

void Floyd(){
	for(int k=0;k<n;k++){
		for(int i=0;i<n;i++){
			for(int j=0;j<n;j++){
				if(dist[i][k]!=INF&&dist[k][j]!=INF&&dist[i][k]+dist[k][j]<dist[i][j]){
					dist[i][j]=dist[i][k]+dist[k][j];
				}
			}
		}
	}
}
int main(){
	memset(dist,INF,sizeof(dist));
	cin>>n;
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			cin>>dist[i][j];
			if(i!=j&&dist[i][j]==0) dist[i][j]=INF;
		}
	}

	Floyd();
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			if(j!=0) cout<<" ";
			if(dist[i][j]==INF){
				cout<<-1;
			}else{
				cout<<dist[i][j];
			}
		}
		cout<<endl;
	}
	return 0;
}

最短路径

题目描述
N个城市，标号从0到N-1，M条道路，第K条道路（K从0开始）的长度为2^K，求编号为0的城市到其他城市的最短距离。
输入
第一行两个正整数N（2<=N<=100）M(M<=500),表示有N个城市，M条道路，
接下来M行两个整数，表示相连的两个城市的编号。
输出
N-1行，表示0号城市到其他城市的最短路，如果无法到达，输出-1，数值太大的以MOD 100000 的结果输出。
样例输入
4 3
0 1
1 2
2 0
样例输出
1
3
-1
程序

//WA代码
//需要高精度，这里不写了
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int MAXV=501;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int dis;
	Node(){}
	Node(int vv,int dd):v(vv),dis(dd){}
	bool operator < (const Node &tmp) const{
		return dis>tmp.dis;
	}
};
vector<Node> Adj[MAXV];
bool bInq[MAXV];
int dist[MAXV];
int n,m;

void Dijkstra(int s){
	memset(bInq,false,sizeof(bInq));
	memset(dist,INF,sizeof(dist));
	dist[s]=0;
	priority_queue<Node> pq;
	pq.push(Node(s,0));
	while(!pq.empty()){
		Node top=pq.top();
		int u=top.v;
		//cout<<"dis:"<<top.dis<<endl;
		pq.pop();
		bInq[u]=true;
		for(int i=0;i<Adj[u].size();i++){
			int v=Adj[u][i].v;
			int dis=Adj[u][i].dis;
			if(!bInq[v]&&dist[u]+dis<dist[v]){
				dist[v]=dist[u]+dis;
				dist[v]%=100000;
				pq.push(Node(v,dist[v]));
			}
		}
	}
}
int cos[MAXV];
int cal(int k){
	if(cos[k]!=INF) return cos[k];
	if(k==0){
		cos[k]=1;
		return cos[k];
	}
	if(k%2==1){
		cos[k]=2*cal(k-1)%100000;
		return cos[k];
	}
	else{
		int mul=cal(k/2)%100000;
		cos[k]=mul*mul%100000;
		return cos[k];
	}
}
int main(){
	memset(cos,INF,sizeof(cos));
//	for(int i=0;i<100;i++){
//		cout<<i<<":"<<cal(i)<<endl;
//		system("pause");
//	}

	cin>>n>>m;
	for(int k=0;k<m;k++){
		int u,v;
		cin>>u>>v;
		Adj[u].push_back(Node(v,cal(k)));
		Adj[v].push_back(Node(u,cal(k)));
	}
	Dijkstra(0);
	for(int i=1;i<n;i++){
		if(dist[i]==INF) dist[i]=-1;
		cout<<dist[i]%100000<<endl;
	}
	return 0;
}

最短路径

题目描述
有n个城市m条道路（n<1000, m<10000)，每条道路有个长度，请找到从起点s到终点t的最短距离和经过的城市名。
输入
输入包含多组测试数据。
每组第一行输入四个数，分别为n，m，s，t。
接下来m行，每行三个数，分别为两个城市名和距离。
输出
每组输出占两行。
第一行输出起点到终点的最短距离。
第二行输出最短路径上经过的城市名，如果有多条最短路径，输出字典序最小的那条。若不存在从起点到终点的路径，则输出“can’t arrive”。
样例输入
3 3 1 3
1 3 3
1 2 1
2 3 1
样例输出
2
1 2 3
程序

#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
using namespace std;
const int MAXV=1001;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int dis;
	Node(){}
	Node(int vv,int dd):v(vv),dis(dd){}
	bool operator < (const Node &tmp) const{
		return dis>tmp.dis;
	}
};
vector< vector<Node> > Adj;
int dist[MAXV];
int pre[MAXV];
bool bInq[MAXV];
int n,m,s,t;

void Dijkstra(int s){
	memset(dist,INF,sizeof(dist));
	memset(bInq,false,sizeof(bInq));
	for(int i=0;i<MAXV;i++) pre[i]=i;
	pre[s]=s;
	dist[s]=0;
	priority_queue<Node> pq;
	pq.push(Node(s,0));
	while(!pq.empty()){
		Node top=pq.top();
		pq.pop();
		int u=top.v;
		bInq[u]=true;
		for(int i=0;i<Adj[u].size();i++){
			int v=Adj[u][i].v;
			int dis=Adj[u][i].dis;
			if(!bInq[v]){
				if(dist[u]+dis<dist[v]){
					dist[v]=dist[u]+dis;
					pre[v]=u;
					pq.push(Node(v,dist[v]));
				}else if(dist[u]+dis==dist[v]){
					if(u<pre[v]){
						pre[v]=u;
					}
				}
			}
		}
	}
}
void print(int v){
	if(v==pre[v]){
		cout<<v;
		return;
	}
	print(pre[v]);
	cout<<" "<<v;
}
bool isPush(int s,int e,int l,int& index){
	for(int i=0;i<Adj[s].size();i++){
		int v=Adj[s][i].v;
		if(v==e){
			index=i;
			return true;
		}
	}
	return false;
}
int main(){
	while(cin>>n>>m>>s>>t){
		Adj.clear();  //注意resize改变vector的size大小，但是尽可能保留原有元素！
		Adj.resize(n+1);
		for(int i=0;i<m;i++){
			int s,e,l;
			cin>>s>>e>>l;
			int index;
			if(isPush(s,e,l,index)){
				int dis=Adj[s][index].dis;
				if(dis>l){
					Adj[s][index].dis=l;
				}
			}else{
				Adj[s].push_back(Node(e,l));
			}
			if(isPush(e,s,l,index)){
				int dis=Adj[e][index].dis;
				if(dis>l){
					Adj[e][index].dis=l;
				}
			}else{
				Adj[e].push_back(Node(s,l));
			}

		}
		Dijkstra(s);
		if(dist[t]==INF) cout<<"can't arrive"<<endl;
		else{
			cout<<dist[t]<<endl;
			print(t);
			cout<<endl;
		}
	}
	return 0;
}

最短路径问题

题目描述
给你n个点，m条无向边，每条边都有长度d和花费p，给你起点s终点t，要求输出起点到终点的最短距离及其花费，如果最短距离有多条路线，则输出花费最少的。
输入
输入n,m，点的编号是1~n,然后是m行，每行4个数 a,b,d,p，表示a和b之间有一条边，且其长度为d，花费为p。最后一行是两个数 s,t;起点s，终点t。n和m为0时输入结束。(1<n<=1000, 0<m<100000, s != t)
输出
输出 一行有两个数， 最短距离及其花费。
样例输入
3 2
1 2 5 6
2 3 4 5
1 3
0 0
样例输出
9 11
程序

#include<iostream>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
const int MAXV=1001;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int dis;
	int cos;
	Node(){}
	Node(int vv,int dd,int cc):v(vv),dis(dd),cos(cc){}
	bool operator < (const Node &tmp) const{
		return dis>tmp.dis;
	}
};
vector< vector<Node> >Adj;
int n,m,s,t;
int dist[MAXV];
int cost[MAXV];
bool bInq[MAXV];

void Dijkstra(int s){
	memset(dist,INF,sizeof(dist));
	memset(cost,INF,sizeof(cost));
	memset(bInq,false,sizeof(bInq));
	dist[s]=0;
	cost[s]=0;
	priority_queue<Node> pq;
	pq.push(Node(s,0,0));
	while(!pq.empty()){
		Node top=pq.top();
		int u=top.v;
		pq.pop();
		for(int i=0;i<Adj[u].size();i++){
			int v=Adj[u][i].v;
			int dis=Adj[u][i].dis;
			int cos=Adj[u][i].cos;
			if(!bInq[v]){
				if(dist[u]+dis<dist[v]){
					dist[v]=dist[u]+dis;
					cost[v]=cost[u]+cos;
					pq.push(Node(v,dist[v],cost[v]));
				}else if(dist[u]+dis==dist[v]){
					if(cost[u]+cos<cost[v]){
						cost[v]=cost[u]+cos;
					}
				}
			}
		}
	}
}
bool isPush(int s,int e,int d,int& index){
	for(int i=0;i<Adj[s].size();i++){
		int v=Adj[s][i].v;
		if(v==e){
			index=i;
			return true;
		}
	}
	return false;
}
int main(){
	while(cin>>n>>m&&n!=0&&m!=0){
		Adj.clear();
		Adj.resize(n+1);
		for(int i=0;i<m;i++){
			int s,e,d,c;
			cin>>s>>e>>d>>c;
			int index;
			if(isPush(s,e,d,index)){
				int dis=Adj[s][index].dis;
				if(dis>d){
					Adj[s][index].dis=d;
				}
			}else{
				Adj[s].push_back(Node(e,d,c));
			}
			if(isPush(e,s,d,index)){
				int dis=Adj[e][index].dis;
				if(dis>d){
					Adj[e][index].dis=d;
				}
			}else{
				Adj[e].push_back(Node(s,d,c));
			}
		}
		cin>>s>>t;
		Dijkstra(s);
		cout<<dist[t]<<" "<<cost[t]<<endl;
	}
	return 0;
}

#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int MAXV=1001;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int dis;
	int cos;
	Node(){}
	Node(int vv,int dd,int cc):v(vv),dis(dd),cos(cc){}
};
int n,m,s,t;
vector< vector<Node> > Adj;
int dist[MAXV];
int num[MAXV];
bool vis[MAXV];
int cost[MAXV];

void SPFA(){
	memset(dist,INF,sizeof(dist));
	memset(num,0,sizeof(num));
	memset(vis,false,sizeof(vis));
	memset(cost,INF,sizeof(cost));
	queue<int> q;
	q.push(s);
	dist[s]=0;
	cost[s]=0;
	vis[s]=true;
	num[s]++;
	while(!q.empty()){
		int u=q.front();
		q.pop();
		vis[u]=false;
		for(int i=0;i<Adj[u].size();i++){
			int v=Adj[u][i].v;
			int dis=Adj[u][i].dis;
			int cos=Adj[u][i].cos;
			if(dist[u]+dis<dist[v]){
				dist[v]=dist[u]+dis;
				cost[v]=cost[u]+cos;

				if(!vis[v]){
					q.push(v);
					vis[v]=true;
					num[v]++;
					if(num[v]==n) break;
				}
			}else if(dist[u]+dis==dist[v]){

				if(cost[u]+cos<cost[v]){
					cost[v]=cost[u]+cos;
				}
			}
		}
	}
}
int main(){
	while(cin>>n>>m&&n!=0){
		Adj.clear();
		Adj.resize(n+1);
		for(int i=0;i<m;i++){
			int a,b,d,p;
			cin>>a>>b>>d>>p;
			Adj[a].push_back(Node(b,d,p));
			Adj[b].push_back(Node(a,d,p));
		}
		cin>>s>>t;
		SPFA();
		cout<<dist[t]<<" "<<cost[t]<<endl;
	}
	return 0;
}

最小生成树

Prim算法

邻接矩阵 $O(V^{2})$

const int MAXV=1000;
const int INF=0x3f3f3f3f;
int n,G[MAXV][MAXV];
int dist[MAXV];
bool vis[MAXV];

int Prim(int s){
  memset(dist,INF,sizeof(dist));
  memset(vis,false,sizeof(vis));
  dist[s]=0;
  int ans=0;
  for(int i=0;i<n;i++){
    int u=-s,MIN=INF;
    for(int j=0;j<n;j++){
      if(!vis[j]&&dist[j]<MIN){
        u=j;
        MIN=dist[j];
      }
    }
    if(u==-1) return -1;
    vis[u]=true;
    ans+=dist[u];
    for(int v=0;v<n;v++){
      if(!vis[v]&&G[u][v]!=INF&&G[u][v]<dist[v]){
        dist[v]=G[u][v];
      }
    }
  }
  return ans;
}

邻接表 $O(V^{2}+E)$

const int MAXV=1000;
const int INF=0x3f3f3f3f;
int n;
struct Node{
  int v;
  int dis;
}
vector<Node> Adj[MAXV];
int dist[MAXV];
bool vis[MAXV];

int Prim(int s){
  memset(dist,INF,sizeof(dist));
  memset(vis,false,sizeof(vis));
  dist[s]=0;
  int ans=0;
  for(int i=0;i<n;i++){
    int u=-1,MIN=INF;
    for(int j=0;j<n;j++){
      if(!vis[j]&&dist[j]<MIN){
        u=j;
        MIN=dist[j];
      }
    }
    if(u==-1) return -1;
    ans+=dist[u];
    vis[u]=true;
    for(int j=0;j<Adj[u].size();j++){
      int v=Adj[u][j].v;
      int dis=Adj[u][j].dis;
      if(!vis[v]&&dis<dist[v]){
        dist[v]=dis;
      }
    }
  }
  return ans;
}

堆优化 $O(VlogV+E)$

const int MAXV=1000;
const int INF=0x3f3f3f3f;
struct Node{
  int v;
  int dis;
  Node(){}
  Node(int vv,int dd):v(vv).dis(dd){}
  bool operator < (const Node &tmp) const{
    return dis>tmp.dis;
  }
}
vector<Node> Adj[MAXV];
int n;
int dist[MAXV];
bool vis[MAXV];

int Prim(int s){
  memset(dist,INF,sizeof(dist));
  memset(vis,false,sizeof(vis));
  dist[s]=0;
  int ans=0;
  int numVertex=0;
  priority_queue<Node> pq;
  pq.push(Node(s,0));
  while(!pq.empty()){
    Node top=pq.top();
    pq.pop();
    int u=top.v;
    if(!vis[u]){
      ans+=top.dis;
      numVertex++;
      if(numVertex==n) break;
    }
    vis[u]=true;

    for(int i=0;i<Adj[u].size();i++){
      int v=Adj[u][i].v;
      int dis=Adj[u][i].dis;
      if(!vis[v]&&dis<dist[v]){
        dist[v]=dis;
        pq.push(Node(v,dist[v]));
      }
    }
  }
  if(numVertex!=n) return -1;//不连通
  return ans;
}

Kruskal算法 $O(ElogE)$

const int MAXV=1001;
const int MAXE=10001;
const int INF=0x3f3f3f3f;
struct Edge{
  int u,v;
  int cos;
  bool operator < (const Edge &tmp) const{
    return cos<tmp.cos;
  }
}
vector<Edge> edges;
int father[MAXV];
void makeSet(){
  for(int i=0;i<MAXV;i++){
    father[i]=i;
  }
}
int findFather(int x){
  if(x==father[x]){
    father[x]=findFather(father[x]);
  }
  return father[x];
}
int Kruskal(int n,int m){
  int ans=0,numEdge=0;
  makeSet();
  sort(edges.begin(),edges.end());
  for(int i=0;i<m;i++){
    int fa=findFather(edges[i].u);
    int fb=findFather(edges[i].v);
    if(fa!=fb){
      father[fa]=fb;
      ans+=edges[i].cos;
      numEdge++;
      if(numEdge==n-1) break;
    }
  }
  if(numEdge!=n-1) return -1;
  else return ans;
}

还是畅通工程

题目描述
某省调查乡村交通状况，得到的统计表中列出了任意两村庄间的距离。省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通（但不一定有直接的公路相连，只要能间接通过公路可达即可），并要求铺设的公路总长度为最小。请计算最小的公路总长度。
输入
测试输入包含若干测试用例。每个测试用例的第1行给出村庄数目N ( < 100 )；随后的N(N-1)/2行对应村庄间的距离，每行给出一对正整数，分别是两个村庄的编号，以及此两村庄间的距离。为简单起见，村庄从1到N编号。
当N为0时，输入结束，该用例不被处理。
输出
对每个测试用例，在1行里输出最小的公路总长度。
样例输入
8
1 2 42
1 3 68
1 4 35
1 5 1
1 6 70
1 7 25
1 8 79
2 3 59
2 4 63
2 5 65
2 6 6
2 7 46
2 8 82
3 4 28
3 5 62
3 6 92
3 7 96
3 8 43
4 5 28
4 6 37
4 7 92
4 8 5
5 6 3
5 7 54
5 8 93
6 7 83
6 8 22
7 8 17
0
样例输出
82
程序

#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
#include<queue>
using namespace std;
const int MAXV=1001;
const int MAXE=10001;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int dis;
	Node(){}
	Node(int vv,int dd):v(vv),dis(dd){}
	bool operator < (const Node &tmp) const{
		return dis>tmp.dis;
	}
};
vector< vector<Node> > Adj;
int dist[MAXV];
int vis[MAXV];
int n;
int Kruskal(int s){
	memset(dist,INF,sizeof(dist));
	memset(vis,false,sizeof(vis));
	dist[s]=0;
	int ans=0;
	int numVertex=0;
	priority_queue<Node> pq;
	pq.push(Node(s,0));
	while(!pq.empty()){
		Node top=pq.top();
		pq.pop();
		int u=top.v;
		if(!vis[u]){
			vis[u]=true;
			ans+=top.dis;
			numVertex++;
			if(numVertex==n) break;
		}else{
			continue;
		}

		for(int i=0;i<Adj[u].size();i++){
			int v=Adj[u][i].v;
			int dis=Adj[u][i].dis;
			if(!vis[v]&&dis<dist[v]){
				dist[v]=dis;
				pq.push(Node(v,dist[v]));
			}
		}
	}
	if(numVertex!=n) return -1;
	return ans;
}
int main(){
	while(cin>>n&&n!=0){
		Adj.clear();
		Adj.resize(n+1);
		for(int i=0;i<n*(n-1)/2;i++){
			int s,e,d;
			cin>>s>>e>>d;
			Adj[s].push_back(Node(e,d));
			Adj[e].push_back(Node(s,d));
		}
		cout<<Kruskal(1)<<endl;
	}
	return 0;
}

#include<iostream>
#include<vector>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXV=1000;
const int INF=0x3f3f3f3f;
struct Edge{
	int u,v;
	int dis;
	Edge(){}
	Edge(int uu,int vv,int dd):u(uu),v(vv),dis(dd){}
	bool operator < (const Edge &tmp) const{
		return dis<tmp.dis;
	}
};
vector<Edge> edges;
int n;
int father[MAXV];

int findFather(int x){
	if(x!=father[x]){
		father[x]=findFather(father[x]);
	}
	return father[x];
}

int main(){
	while(cin>>n&&n!=0){
		edges.clear();
		for(int i=0;i<n;i++) father[i]=i;
		for(int i=0;i<n*(n-1)/2;i++){
			int s,e,d;
			cin>>s>>e>>d;
			edges.push_back(Edge(s,e,d));
		}
		sort(edges.begin(),edges.end());
		int ans=0;
		int numEdge=0;
		for(int i=0;i<edges.size();i++){
			int fa=findFather(edges[i].u);
			int fb=findFather(edges[i].v);
			if(fa!=fb){
				father[fa]=fb;
				ans+=edges[i].dis;
				numEdge++;
				if(numEdge==n-1) break;
			}
		}
		if(numEdge!=n-1) return -1;
		cout<<ans<<endl;
	}
	return 0;
}

Freckles

题目描述
In an episode of the Dick Van Dyke show, little Richie connects the freckles on his Dad’s back to form a picture of the Liberty Bell. Alas, one of the freckles turns out to be a scar, so his Ripley’s engagement falls through.
Consider Dick’s back to be a plane with freckles at various (x,y) locations. Your job is to tell Richie how to connect the dots so as to minimize the amount of ink used. Richie connects the dots by drawing straight lines between pairs, possibly lifting the pen between lines. When Richie is done there must be a sequence of connected lines from any freckle to any other freckle.
输入
The first line contains 0 < n <= 100, the number of freckles on Dick’s back. For each freckle, a line follows; each following line contains two real numbers indicating the (x,y) coordinates of the freckle.
输出
Your program prints a single real number to two decimal places: the minimum total length of ink lines that can connect all the freckles.
样例输入
3
2723.62 7940.81
8242.67 11395.00
4935.54 6761.32
9
10519.52 11593.66
12102.35 2453.15
7235.61 10010.83
211.13 4283.23
5135.06 1287.85
2337.48 2075.61
6279.72 13928.13
65.79 1677.86
5324.26 125.56
0
样例输出
8199.56
32713.73
程序
本站第二个样例结果应该是.74而非.73，因此WA
牛客网同样的题，Accepted！

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
#include<queue>
#include<cmath>
using namespace std;
const int MAXV=1000;
const int MAXE=10001;
const int INF=0x3f3f3f3f;
struct Dot{
	double x,y;
	Dot(){}
	Dot(double xx,double yy):x(xx),y(yy){}
};
struct Node{
	int v;
	double dis;
	Node(){}
	Node(int vv,double dd):v(vv),dis(dd){}
	bool operator < (const Node &tmp) const{
		return dis>tmp.dis;
	}
};
int n;
vector<Dot> dots;
vector< vector<Node> > Adj;
double dist[MAXV];
int vis[MAXV];

double Prim(int s){
	memset(vis,false,sizeof(vis));
	for(int i=0;i<MAXV;i++) dist[i]=INF;
//	cout<<dist[0]<<endl;
//	system("pause");
	dist[s]=0;
	priority_queue<Node> pq;
	pq.push(Node(s,0));
	int nCount=0;
	double ans=0;
	while(!pq.empty()){
		Node top=pq.top();
		pq.pop();
		int u=top.v;
		if(!vis[u]){
			ans+=top.dis;
			vis[u]=true;
			nCount++;
			if(nCount==n) break;
		}else continue;
		for(int i=0;i<Adj[u].size();i++){
			int v=Adj[u][i].v;
			double dis=Adj[u][i].dis;
			if(!vis[v]&&dis<dist[v]){
				dist[v]=dis;
				pq.push(Node(v,dist[v]));
			}
		}
	}
	if(nCount!=n) return -1;
	return ans;
}
double calDis(Dot a, Dot b){
	double dis;
	dis=sqrt(pow(a.x-b.x,2)+pow(a.y-b.y,2));
	return dis;
}
int main(){
	while(cin>>n&&n!=0){
		Adj.clear();
		Adj.resize(n);
		dots.clear();
		for(int i=0;i<n;i++){
			double x,y;
			cin>>x>>y;
			dots.push_back(Dot(x,y));
		}
		for(int i=0;i<n;i++){
			for(int j=0;j<n;j++){
				if(i!=j){
					double dis=calDis(dots[i],dots[j]);

					Adj[i].push_back(Node(j,dis));
				}
			}
		}

		printf("%.2f\n",Prim(0));
	}
	return 0;
}

#include<iostream>
#include<vector>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int MAXV=1000;
const int INF=0x3f3f3f3f;
struct Dot{
	double x,y;
	Dot(){}
	Dot(double xx,double yy):x(xx),y(yy){}
};
struct Edge{
	int u,v;
	double dis;
	Edge(){}
	Edge(int uu,int vv,double dd):u(uu),v(vv),dis(dd){}
	bool operator < (const Edge &tmp) const{
		return dis<tmp.dis;
	}
};
vector<Dot> dots;
vector<Edge> edges;
int n;
int father[MAXV];

int findFather(int x){
	if(x!=father[x]){
		father[x]=findFather(father[x]);
	}
	return father[x];
}

double calDis(Dot a, Dot b){
	return sqrt(pow(a.x-b.x,2)+pow(a.y-b.y,2));
}

int main(){
	while(cin>>n&&n!=0){
		dots.clear();
		dots.resize(n);
		for(int i=0;i<n;i++){
			cin>>dots[i].x>>dots[i].y;
		}
		edges.clear();
		for(int i=0;i<n;i++){
			for(int j=0;j<n;j++){
				if(i!=j){
					double dis=calDis(dots[i],dots[j]);
					edges.push_back(Edge(i,j,dis));
				}
			}
		}
		for(int i=0;i<n;i++) father[i]=i;
		sort(edges.begin(),edges.end());
		double ans=0;
		int numEdge=0;
		for(int i=0;i<edges.size();i++){
			int fa=findFather(edges[i].u);
			int fb=findFather(edges[i].v);
			if(fa!=fb){
				father[fa]=fb;
				ans+=edges[i].dis;
				numEdge++;
				if(numEdge==n-1) break;
			}
		}
		if(numEdge!=n-1) return -1;
		printf("%.2f\n",ans);
	}
	return 0;
}

畅通工程

题目描述
省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通（但不一定有直接的公路相连，只要能间接通过公路可达即可）。经过调查评估，得到的统计表中列出了有可能建设公路的若干条道路的成本。现请你编写程序，计算出全省畅通需要的最低成本。
输入
测试输入包含若干测试用例。每个测试用例的第1行给出评估的道路条数 N、村庄数目M (N, M <=100 )；随后的 N 行对应村庄间道路的成本，每行给出一对正整数，分别是两个村庄的编号，以及此两村庄间道路的成本（也是正整数）。为简单起见，村庄从1到M编号。当N为0时，全部输入结束，相应的结果不要输出。
输出
对每个测试用例，在1行里输出全省畅通需要的最低成本。若统计数据不足以保证畅通，则输出“?”。
样例输入
3 4
1 2 1
2 3 2
3 4 3
2 4
1 2 1
3 4 2
0 5
样例输出
6
?
程序

#include<iostream>
#include<vector>
#include<cstring>
#include<queue>
using namespace std;
const int MAXV=1000;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int dis;
	Node(){}
	Node(int vv,int dd):v(vv),dis(dd){}
	bool operator < (const Node &tmp) const{
		return dis>tmp.dis;
	}
};
int n,m;
int dist[MAXV];
bool vis[MAXV];
vector< vector<Node> > Adj;

int Prim(int s){
	memset(dist,INF,sizeof(dist));
	memset(vis,false,sizeof(vis));
	dist[s]=0;
	priority_queue<Node> pq;
	pq.push(Node(s,0));
	int ans=0;
	int nCount=0;
	while(!pq.empty()){
		Node top=pq.top();
		pq.pop();
		int u=top.v;
		if(!vis[u]){
			vis[u]=true;
			ans+=top.dis;
			nCount++;
			if(nCount==m) break;
		}else continue;
		for(int i=0;i<Adj[u].size();i++){
			int v=Adj[u][i].v;
			int dis=Adj[u][i].dis;
			if(!vis[v]&&dis<dist[v]){
				dist[v]=dis;
				pq.push(Node(v,dist[v]));
			}
		}
	}
	if(nCount!=m) return -1;
	return ans;
}
int main(){
	while(cin>>n>>m&&n!=0){
		Adj.clear();
		Adj.resize(m+1);
		for(int i=0;i<n;i++){
			int s,e,l;
			cin>>s>>e>>l;
			Adj[s].push_back(Node(e,l));
			Adj[e].push_back(Node(s,l));
		}
		int dis=Prim(1);
		if(dis==-1) cout<<"?"<<endl;
		else cout<<dis<<endl;
	}
	return 0;
}

#include<iostream>
#include<vector>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int MAXV=1000;
const int INF=0x3f3f3f3f;
struct Edge{
	int u,v;
	int dis;
	Edge(){}
	Edge(int uu,int vv,int dd):u(uu),v(vv),dis(dd){}
	bool operator < (const Edge &tmp) const{
		return dis<tmp.dis;
	}
};
vector<Edge> edges;
int n,m;
int father[MAXV];

int findFather(int x){
	if(x!=father[x]){
		father[x]=findFather(father[x]);
	}
	return father[x];
}

int main(){
	while(cin>>n>>m&&n!=0){
		edges.clear();
		for(int i=0;i<n;i++){
			int s,e,d;
			cin>>s>>e>>d;
			edges.push_back(Edge(s,e,d));
		}
		for(int i=1;i<=m;i++) father[i]=i;
		sort(edges.begin(),edges.end());
		int ans=0;
		int numEdge=0;
		for(int i=0;i<edges.size();i++){
			int fa=findFather(edges[i].u);
			int fb=findFather(edges[i].v);
			if(fa!=fb){
				father[fa]=fb;
				ans+=edges[i].dis;
				numEdge++;
				if(numEdge==m-1) break;
			}
		}
		if(numEdge!=m-1) cout<<"?"<<endl;
		else cout<<ans<<endl;
	}
	return 0;
}

继续畅通工程

题目描述
省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通（但不一定有直接的公路相连，只要能间接通过公路可达即可）。现得到城镇道路统计表，表中列出了任意两城镇间修建道路的费用，以及该道路是否已经修通的状态。现请你编写程序，计算出全省畅通需要的最低成本。
输入
测试输入包含若干测试用例。每个测试用例的第1行给出村庄数目N ( 1 < N < 100 )；随后的 N(N-1)/2 行对应村庄间道路的成本及修建状态，每行给4个正整数，分别是两个村庄的编号（从1编号到N），此两村庄间道路的成本，以及修建状态：1表示已建，0表示未建。
当N为0时输入结束。
输出
每个测试用例的输出占一行，输出全省畅通需要的最低成本。
样例输入
4
1 2 1 1
1 3 6 0
1 4 2 1
2 3 3 0
2 4 5 0
3 4 4 0
3
1 2 1 1
2 3 2 1
1 3 1 0
0
样例输出
3
0
程序

#include<iostream>
#include<vector>
#include<cstring>
#include<queue>
using namespace std;
const int MAXV=1000;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int dis;
	Node(){}
	Node(int vv,int dd):v(vv),dis(dd){}
	bool operator < (const Node &tmp) const{
		return dis>tmp.dis;
	}
};
int n;
vector< vector<Node> > Adj;
int dist[MAXV];
bool vis[MAXV];

int main(){
	while(cin>>n&&n!=0){
		memset(dist,INF,sizeof(dist));
		memset(vis,false,sizeof(vis));
		priority_queue<Node> pq;
		Adj.clear();
		Adj.resize(n+1);
		bool bStart=false;
		for(int i=0;i<n*(n-1)/2;i++){
			int s,e,d,f;
			cin>>s>>e>>d>>f;
			if(f==1){
				pq.push(Node(s,0));
				pq.push(Node(e,0));
				bStart=true;
			}else{
				Adj[s].push_back(Node(e,d));
				Adj[e].push_back(Node(s,d));
			}
		}
		if(!bStart){
			dist[1]=0;
			pq.push(Node(1,0));
		}
		int ans=0;
		int nCount=0;
		while(!pq.empty()){
			Node top=pq.top();
			pq.pop();
			int u=top.v;
			if(!vis[u]){
				vis[u]=true;
				ans+=top.dis;
				nCount++;
				if(nCount==n) break;
			}else continue;
			for(int i=0;i<Adj[u].size();i++){
				int v=Adj[u][i].v;
				int dis=Adj[u][i].dis;
				if(!vis[v]&&dis<dist[v]){
					dist[v]=dis;
					pq.push(Node(v,dist[v]));
				}
			}
		}
		if(nCount!=n) return -1;
		else cout<<ans<<endl;
	}
	return 0;
}

#include<iostream>
#include<vector>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int MAXV=1000;
const int INF=0x3f3f3f3f;
struct Edge{
	int u,v;
	int dis;
	Edge(){}
	Edge(int uu,int vv,int dd):u(uu),v(vv),dis(dd){}
	bool operator < (const Edge &tmp) const{
		return dis<tmp.dis;
	}
};
vector<Edge> edges;
int n;
int father[MAXV];

int findFather(int x){
	if(x!=father[x]){
		father[x]=findFather(father[x]);
	}
	return father[x];
}

int main(){
	while(cin>>n&&n!=0){
		edges.clear();
		for(int i=1;i<=n;i++) father[i]=i;
		for(int i=0;i<n*(n-1)/2;i++){
			int s,e,d,k;
			cin>>s>>e>>d>>k;
			if(k==1){
				int fa=findFather(s);
				int fb=findFather(e);
				if(fa!=fb){
					father[fa]=fb;
				}
			}else{
				edges.push_back(Edge(s,e,d));
			}
		}
		sort(edges.begin(),edges.end());
		int ans=0;
		for(int i=0;i<edges.size();i++){
			int fa=findFather(edges[i].u);
			int fb=findFather(edges[i].v);
			if(fa!=fb){
				father[fa]=fb;
				ans+=edges[i].dis;
			}
		}
		cout<<ans<<endl;
	}
	return 0;
}

Jungle Roads

题目描述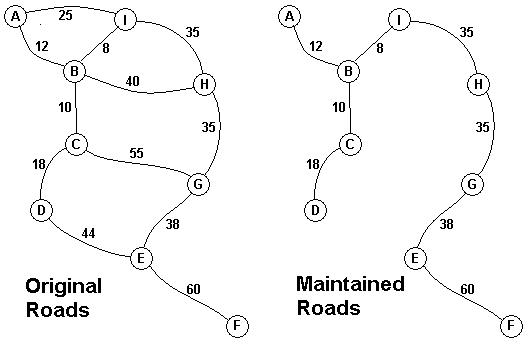

The Head Elder of the tropical island of Lagrishan has a problem. A burst of foreign aid money was spent on extra roads between villages some years ago. But the jungle overtakes roads relentlessly, so the large road network is too expensive to maintain. The Council of Elders must choose to stop maintaining some roads. The map above on the left shows all the roads in use now and the cost in aacms per month to maintain them. Of course there needs to be some way to get between all the villages on maintained roads, even if the route is not as short as before. The Chief Elder would like to tell the Council of Elders what would be the smallest amount they could spend in aacms per month to maintain roads that would connect all the villages. The villages are labeled A through I in the maps above. The map on the right shows the roads that could be maintained most cheaply, for 216 aacms per month. Your task is to write a program that will solve such problems.
输入
The input consists of one to 100 data sets, followed by a final line containing only 0. Each data set starts with a line containing only a number n, which is the number of villages, 1 < n < 27, and the villages are labeled with the first n letters of the alphabet, capitalized. Each data set is completed with n-1 lines that start with village labels in alphabetical order. There is no line for the last village. Each line for a village starts with the village label followed by a number, k, of roads from this village to villages with labels later in the alphabet. If k is greater than 0, the line continues with data for each of the k roads. The data for each road is the village label for the other end of the road followed by the monthly maintenance cost in aacms for the road. Maintenance costs will be positive integers less than 100. All data fields in the row are separated by single blanks. The road network will always allow travel between all the villages. The network will never have more than 75 roads. No village will have more than 15 roads going to other villages (before or after in the alphabet). In the sample input below, the first data set goes with the map above.
输出
The output is one integer per line for each data set: the minimum cost in aacms per month to maintain a road system that connect all the villages. Caution: A brute force solution that examines every possible set of roads will not finish within the one minute time limit.
样例输入
3
A 1 B 42
B 1 C 87
6
A 2 B 13 E 55
B 1 C 1
C 1 D 20
D 1 E 4
E 1 F 76
0
样例输出
129
114
程序

#include<iostream>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
const int MAXV=100;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int dis;
	Node(){}
	Node(int vv,int dd):v(vv),dis(dd){}
	bool operator < (const Node &tmp)const{
		return dis>tmp.dis;
	}
};
vector< vector<Node> > Adj;
int dist[MAXV];
bool vis[MAXV];
int n;
int Prim(int s){
	memset(dist,INF,sizeof(dist));
	memset(vis,false,sizeof(vis));
	dist[s]=0;
	priority_queue<Node> pq;
	pq.push(Node(s,0));
	int ans=0;
	int nCount=0;
	while(!pq.empty()){
		Node top=pq.top();
		pq.pop();
		int u=top.v;
		if(!vis[u]){
			vis[u]=true;
			nCount++;
			ans+=top.dis;
			if(nCount==n) break;
		}else continue;
		for(int i=0;i<Adj[u].size();i++){
			int v=Adj[u][i].v;
			int dis=Adj[u][i].dis;
			if(!vis[v]&&dis<dist[v]){
				dist[v]=dis;
				pq.push(Node(v,dist[v]));
			}
		}
	}
	if(nCount!=n) return -1;
	return ans;
}
int main(){
	while(cin>>n&&n!=0){
		Adj.clear();
		Adj.resize(n);
		for(int i=0;i<n-1;i++){
			char s,e;
			int k,d;
			cin>>s>>k;
			for(int j=0;j<k;j++){
				cin>>e>>d;
				Adj[s-'A'].push_back(Node(e-'A',d));
				Adj[e-'A'].push_back(Node(s-'A',d));
			}
		}
		cout<<Prim(0)<<endl;
	}
	return 0;
}

#include<iostream>
#include<vector>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int MAXV=1000;
const int INF=0x3f3f3f3f;
struct Edge{
	int u,v;
	int dis;
	Edge(){}
	Edge(int uu,int vv,int dd):u(uu),v(vv),dis(dd){}
	bool operator < (const Edge &tmp) const{
		return dis<tmp.dis;
	}
};
vector<Edge> edges;
int n;
int father[MAXV];

int findFather(int x){
	if(x!=father[x]){
		father[x]=findFather(father[x]);
	}
	return father[x];
}

int main(){
	while(cin>>n&&n!=0){
		edges.clear();
		for(int i=0;i<n;i++) father[i]=i;
		for(int i=0;i<n-1;i++){
			char s,e;
			int k,d;
			cin>>s>>k;
			for(int j=0;j<k;j++){
				cin>>e>>d;
				edges.push_back(Edge(s-'A',e-'A',d));
			}
		}
		sort(edges.begin(),edges.end());
		int ans=0;
		for(int i=0;i<edges.size();i++){
			int fa=findFather(edges[i].u);
			int fb=findFather(edges[i].v);
			if(fa!=fb){
				father[fa]=fb;
				ans+=edges[i].dis;
			}
		}
		cout<<ans<<endl;
	}
	return 0;
}

拓扑排序

如果一个有向图的任意顶点都无法通过一些有向边回到自身，那么称这个有向图为有向无环图（Directed Acyclic Grah, DAG）

• 算法思路：
• ①定义一个队列Q，并把所有入度为0的节点加入队列
• ②取队首节点，输出。然后删除所有从它出发的边，并令这些边到达的顶点入度减1，如果某个顶点的入度减为0，则将其加入队列。
• ③反复进行②操作，直到队列为空。如果队列为空时入过队的节点数目恰好为N，说明拓扑排序成功，图G为有向无环图；否则，拓扑排序失败，图G中有环。

  const int MAXV=1000;
  const int INF=0x3f3f3f3f;
  vector<int> Adj[MAXV];
  int n,m,inDegree[MAXV];
  bool topologicalSort(){
    int num=0;
    queue<int> q;
    for(int i=0;i<n;i++){
      if(inDegree[i]==0){
        p.push(i);
      }
    }
    while(!q.empty()){
      int u=q.front();
      //cout<<u;
      q.pop();
      for(int i=0;i<Adj[u].size();i++){
        int v=Adj[u][i];
        inDegree[v]--;
        if(inDegree[v]==0){
          q.push(v);
        }
      }
      //Adj[u].clear();
      num++;
    }
    if(num!=n) return false;
    else return true;
  }

  算法7-12：有向无环图的拓扑排序

题目描述
由某个集合上的一个偏序得到该集合上的一个全序，这个操作被称为拓扑排序。偏序和全序的定义分别如下：
若集合X上的关系R是自反的、反对称的和传递的，则称R是集合X上的偏序关系。
设R是集合X上的偏序，如果对每个x,y∈X必有xRy或yRx，则称R是集合X上的全序关系。
由偏序定义得到拓扑有序的操作便是拓扑排序。
拓扑排序的流程如下：
1.在有向图中选一个没有前驱的顶点并且输出之；
2.从图中删除该顶点和所有以它为尾的弧。
重复上述两步，直至全部顶点均已输出，或者当前图中不存在无前驱的顶点为止。后一种情况则说明有向图中存在环。
在本题中，读入一个有向图的邻接矩阵（即数组表示），建立有向图并按照以上描述中的算法判断此图是否有回路，如果没有回路则输出拓扑有序的顶点序列。
输入
输入的第一行包含一个正整数n，表示图中共有n个顶点。其中n不超过50。
以后的n行中每行有n个用空格隔开的整数0或1，对于第i行的第j个整数，如果为1，则表示第i个顶点有指向第j个顶点的有向边，0表示没有i指向j的有向边。当i和j相等的时候，保证对应的整数为0。
输出
如果读入的有向图含有回路，请输出“ERROR”，不包括引号。
如果读入的有向图不含有回路，请按照题目描述中的算法依次输出图的拓扑有序序列，每个整数后输出一个空格。
请注意行尾输出换行。
样例输入
4
0 1 0 0
0 0 1 0
0 0 0 0
0 0 1 0
样例输出
3 0 1 2
程序

#include<iostream>
#include<stack>
#include<vector>
#include<cstring>
using namespace std;
const int MAXV=100;
const int INF=0x3f3f3f3f;
vector< vector<int> > Adj;
vector<int> result;
int inDegree[MAXV];
int n;
bool topologicalSort(){
	stack<int> s;
	for(int i=0;i<n;i++){
		if(inDegree[i]==0){
			s.push(i);
		}
	}
	int num=0;
	while(!s.empty()){
		int u=s.top();
		s.pop();
		result.push_back(u);
		num++;
		for(int i=0;i<Adj[u].size();i++){
			int v=Adj[u][i];
			inDegree[v]--;
			if(inDegree[v]==0) s.push(v);
		}
	}
	if(num!=n) return false;
	else return true;
}
int main(){
	while(cin>>n){
		Adj.clear();
		Adj.resize(n);
		memset(inDegree,0,sizeof(inDegree));
		for(int i=0;i<n;i++){
			for(int j=0;j<n;j++){
				int tmp;
				cin>>tmp;
				if(tmp!=0){
					Adj[i].push_back(j);
					inDegree[j]++;
				}
			}
		}
		if(topologicalSort()){
			for(int i=0;i<result.size();i++){
				if(i!=0) cout<<" ";
				cout<<result[i];
			}
			cout<<endl;
		}else cout<<"ERROR"<<endl;
	}
	return 0;
}

确定比赛名次

题目描述
有N个比赛队（1<=N<=500），编号依次为1，2，3，。。。。，N进行比赛，比赛结束后，裁判委员会要将所有参赛队伍从前往后依次排名，但现在裁判委员会不能直接获得每个队的比赛成绩，只知道每场比赛的结果，即P1赢P2，用P1，P2表示，排名时P1在P2之前。现在请你编程序确定排名。
输入
输入有若干组，每组中的第一行为二个数N（1<=N<=500），M；其中N表示队伍的个数，M表示接着有M行的输入数据。接下来的M行数据中，每行也有两个整数P1，P2表示即P1队赢了P2队。
输出
给出一个符合要求的排名。输出时队伍号之间有空格，最后一名后面没有空格。
其他说明：符合条件的排名可能不是唯一的，此时要求输出时编号小的队伍在前；输入数据保证是正确的，即输入数据确保一定能有一个符合要求的排名。
样例输入
3 2
3 1
3 2
17 16
16 1
13 2
7 3
12 4
12 5
17 6
10 7
11 8
11 9
16 10
13 11
15 12
15 13
17 14
17 15
17 16
0 0
样例输出
3 1 2
17 6 14 15 12 4 5 13 2 11 8 9 16 1 10 7 3
程序

#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
const int MAXV=501;
vector< vector<int> > Adj;
int inDegree[MAXV];
int n,m;
struct MyCmp{
	bool operator () (const int &a,const int &b) const{
		return a>b;
	}
};
bool topologicalSort(){
	priority_queue<int,vector<int>,MyCmp> pq;
	for(int i=1;i<=n;i++){
		if(inDegree[i]==0){
			pq.push(i);
		}
	}
	int num=0;
	bool bFirst=true;
	while(!pq.empty()){
		int u=pq.top();
		pq.pop();
		if(!bFirst) cout<<" ";
		else bFirst=false;
		num++;
		cout<<u;
		for(int i=0;i<Adj[u].size();i++){
			int v=Adj[u][i];
			inDegree[v]--;
			if(inDegree[v]==0){
				pq.push(v);
			}
		}
	}
	if(num==n) return true;
	else return false;
}
int main(){
	while(cin>>n>>m&&n!=0){
		Adj.clear();
		Adj.resize(n+1);
		memset(inDegree,0,sizeof(inDegree));
		for(int i=0;i<m;i++){
			int s,e;
			cin>>s>>e;
			Adj[s].push_back(e);
			inDegree[e]++;
		}
		topologicalSort();
		cout<<endl;
	}
	return 0;
}

Legal or Not

题目描述
ACM-DIY is a large QQ group where many excellent acmers get together. It is so harmonious that just like a big family. Every day,many “holy cows” like HH, hh, AC, ZT, lcc, BF, Qinz and so on chat on-line to exchange their ideas. When someone has questions, many warm-hearted cows like Lost will come to help. Then the one being helped will call Lost “master”, and Lost will have a nice “prentice”. By and by, there are many pairs of “master and prentice”. But then problem occurs: there are too many masters and too many prentices, how can we know whether it is legal or not?We all know a master can have many prentices and a prentice may have a lot of masters too, it’s legal. Nevertheless，some cows are not so honest, they hold illegal relationship. Take HH and 3xian for instant, HH is 3xian’s master and, at the same time, 3xian is HH’s master,which is quite illegal! To avoid this,please help us to judge whether their relationship is legal or not. Please note that the “master and prentice” relation is transitive. It means that if A is B’s master ans B is C’s master, then A is C’s master.
输入
The input consists of several test cases. For each case, the first line contains two integers, N (members to be tested) and M (relationships to be tested)(2 <= N, M <= 100). Then M lines follow, each contains a pair of (x, y) which means x is y’s master and y is x’s prentice. The input is terminated by N = 0.TO MAKE IT SIMPLE, we give every one a number (0, 1, 2,…, N-1). We use their numbers instead of their names.
输出
For each test case, print in one line the judgement of the messy relationship.If it is legal, output “YES”, otherwise “NO”.
样例输入
4 3
0 1
1 2
2 3
3 3
0 1
1 2
2 0
0 1
样例输出
YES
NO
程序

#include<iostream>
#include<queue>
#include<vector>
#include<cstring>
using namespace std;
const int MAXV=101;
vector< vector<int> > Adj;
int inDegree[MAXV];
int n,m;

bool topologicalSort(){
	queue<int> q;
	for(int i=0;i<n;i++){
		if(inDegree[i]==0) q.push(i);
	}
	int num=0;
	while(!q.empty()){
		int u=q.front();
		q.pop();
		num++;
		for(int i=0;i<Adj[u].size();i++){
			int v=Adj[u][i];
			inDegree[v]--;
			if(inDegree[v]==0) q.push(v);
		}
	}
	if(num!=n) return false;
	else return true;
}
int main(){
	while(cin>>n>>m&&n!=0){
		Adj.clear();
		Adj.resize(n);
		memset(inDegree,0,sizeof(inDegree));
		for(int i=0;i<m;i++){
			int s,e;
			cin>>s>>e;
			Adj[s].push_back(e);
			inDegree[e]++;
		}
		if(topologicalSort()) cout<<"YES"<<endl;
		else cout<<"NO"<<endl;
	}
	return 0;
}

剑指 Offer II 114. 外星文字典

Description
现有一种使用英语字母的外星文语言，这门语言的字母顺序与英语顺序不同。

给定一个字符串列表 words ，作为这门语言的词典，words 中的字符串已经 按这门新语言的字母顺序进行了排序 。

请你根据该词典还原出此语言中已知的字母顺序，并 按字母递增顺序 排列。若不存在合法字母顺序，返回 “” 。若存在多种可能的合法字母顺序，返回其中 任意一种 顺序即可。

字符串 s 字典顺序小于 字符串 t 有两种情况：

在第一个不同字母处，如果 s 中的字母在这门外星语言的字母顺序中位于 t 中字母之前，那么 s 的字典顺序小于 t 。
如果前面 min(s.length, t.length) 字母都相同，那么 s.length < t.length 时，s 的字典顺序也小于 t 。

Example
示例 1：
输入：words = [“wrt”,”wrf”,”er”,”ett”,”rftt”]
输出：”wertf”

示例 2：
输入：words = [“z”,”x”]
输出：”zx”

示例 3：
输入：words = [“z”,”x”,”z”]
输出：””
解释：不存在合法字母顺序，因此返回 “” 。

提示：
1 <= words.length <= 100
1 <= words[i].length <= 100
words[i] 仅由小写英文字母组成

Program

拓扑排序
关键是构图，理解错了，还以为只是每个word排了序，原来是words排序。

class Solution {
private:
    vector<vector<int>> Adj;
    vector<int> inDegree;
    unordered_map<char, int> cToi;
    unordered_map<int, char> iToc;

    queue<int> q;
    int cnt = 0;
    void statisticChars(const vector<string>& words){
        for(string str:words){
            for(char ch:str){
                if(cToi.find(ch) == cToi.end()){
                    cToi[ch] = cnt;
                    iToc[cnt ++] = ch;
                }
            }
        }
    }
public:
    string alienOrder(vector<string>& words) {
        // 统计出现的字符数并进行编码
        statisticChars(words);
        
        Adj.resize(cnt);
        inDegree.resize(cnt, 0);
        
        // 构造邻接表
        for(int i = 1; i < words.size(); i ++){
            int n = min(words[i - 1].length(), words[i].length());
            int j = 0;
            while(j < n){
                char ch1 = words[i - 1][j], ch2 = words[i][j];
                if(ch1 != ch2){
                    Adj[cToi[ch1]].push_back(cToi[ch2]);
                    inDegree[cToi[ch2]] ++;
                    break; //后面无法判断
                }
                j ++;
            }
            if(j == n && words[i - 1].length() > words[i].length()) return {}; //["abc", "ab"] 这种样例真恶心
        }
        
        // 拓扑排序
        for(int u = 0; u < cnt; u ++){
            if(inDegree[u] == 0) q.push(u);
        }

        string res;
        while(!q.empty()){
            int u = q.front(); q.pop();
            res += iToc[u];
            for(int v:Adj[u]){
                inDegree[v] --;
                if(inDegree[v] == 0) q.push(v);
            }
        }
        return res.length() == cnt ? res : "";
    }
};

剑指 Offer II 115. 重建序列

Description
请判断原始的序列 org 是否可以从序列集 seqs 中唯一地 重建 。

序列 org 是 1 到 n 整数的排列，其中 1 ≤ n ≤ 104。重建 是指在序列集 seqs 中构建最短的公共超序列，即 seqs 中的任意序列都是该最短序列的子序列。

Example
示例 1：
输入: org = [1,2,3], seqs = [[1,2],[1,3]]
输出: false
解释：[1,2,3] 不是可以被重建的唯一的序列，因为 [1,3,2] 也是一个合法的序列。

示例 2：
输入: org = [1,2,3], seqs = [[1,2]]
输出: false
解释：可以重建的序列只有 [1,2]。

示例 3：
输入: org = [1,2,3], seqs = [[1,2],[1,3],[2,3]]
输出: true
解释：序列 [1,2], [1,3] 和 [2,3] 可以被唯一地重建为原始的序列 [1,2,3]。

示例 4：
输入: org = [4,1,5,2,6,3], seqs = [[5,2,6,3],[4,1,5,2]]
输出: true

提示：
1 <= n <= 104
org 是数字 1 到 n 的一个排列
1 <= segs[i].length <= 105
seqs[i][j] 是 32 位有符号整数

Program

拓扑排序

class Solution {
private:
    vector<vector<int>> Adj;
    vector<int> inDegree;
    queue<int> q;
    vector<int> res;
    set<int> st;
    int n;
public:
    bool sequenceReconstruction(vector<int>& org, vector<vector<int>>& seqs) {
        n = org.size();
        // 判断seqs内的元素是否是[1, n]
        for(vector<int>& vec:seqs){
            for(int x:vec){
                st.insert(x);
            }
        }
        vector<int> vec(st.begin(), st.end());
        // 判断是否非法
        if(vec.size() != n) return false;
        for(int i = 1; i <= n; i ++){
            if(vec[i - 1] != i) return false;
        }

        // 拓扑排序
        // 构建邻接表
        Adj.resize(n + 1);
        inDegree.resize(n + 1, 0);
        
        for(vector<int>& vec:seqs){
            for(int i = 1; i < vec.size(); i ++){
                int u = vec[i - 1], v = vec[i];
                Adj[u].push_back(v);
                inDegree[v] ++;
            }
        }

        for(int u = 1; u <= n; u ++){
            if(inDegree[u] == 0) q.push(u);
        }

        while(!q.empty() && q.size() == 1){
            int u = q.front(); q.pop();
            res.push_back(u);
            for(int v:Adj[u]){
                inDegree[v] --;
                if(inDegree[v] == 0) q.push(v);
            }
        }
        return res.size() == n && res == org;
    }
};

1632. 矩阵转换后的秩

Description
给你一个 m x n 的矩阵 matrix ，请你返回一个新的矩阵 answer ，其中 answer[row][col] 是 matrix[row][col] 的秩。

每个元素的 秩 是一个整数，表示这个元素相对于其他元素的大小关系，它按照如下规则计算：

秩是从 1 开始的一个整数。
如果两个元素 p 和 q 在 同一行 或者 同一列 ，那么：

• 如果 p < q ，那么 rank(p) < rank(q)
• 如果 p == q ，那么 rank(p) == rank(q)
• 如果 p > q ，那么 rank(p) > rank(q)
• 秩 需要越 小 越好。

题目保证按照上面规则 answer 数组是唯一的。

Example
示例 1：
输入：matrix = [[1,2],[3,4]]
输出：[[1,2],[2,3]]
解释：
matrix[0][0] 的秩为 1 ，因为它是所在行和列的最小整数。
matrix[0][1] 的秩为 2 ，因为 matrix[0][1] > matrix[0][0] 且 matrix[0][0] 的秩为 1 。
matrix[1][0] 的秩为 2 ，因为 matrix[1][0] > matrix[0][0] 且 matrix[0][0] 的秩为 1 。
matrix[1][1] 的秩为 3 ，因为 matrix[1][1] > matrix[0][1]， matrix[1][1] > matrix[1][0] 且 matrix[0][1] 和 matrix[1][0] 的秩都为 2 。

示例 2：
输入：matrix = [[7,7],[7,7]]
输出：[[1,1],[1,1]]

示例 3：
输入：matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]
输出：[[4,2,3],[1,3,4],[5,1,6],[1,3,4]]

示例 4：
输入：matrix = [[7,3,6],[1,4,5],[9,8,2]]
输出：[[5,1,4],[1,2,3],[6,3,1]]

提示：
m == matrix.length
n == matrix[i].length
1 <= m, n <= 500
$-10^9 <= matrix[row][col] <= 10^9$

Program
优先队列 + 标记数组（错误思路）
详见代码，不啰嗦；
错误原因，虽然优先队列保证值小的先出队列，但是不能保证同行同列中同值的秩相同！

class Solution {
private:
    struct Node{
        int r, c;
        int val;
        Node(int _r, int _c, int _val):r(_r), c(_c), val(_val){}
        bool operator < (const Node& other) const{
            return val > other.val;
        }
    };
    int m, n;
    vector<pair<int,int>> rowMarked, colMarked;
    priority_queue<Node> pq;
    vector<vector<int>> res;
public:
    vector<vector<int>> matrixRankTransform(vector<vector<int>>& matrix) {
        m = matrix.size(), n = matrix[0].size();
        rowMarked.resize(m, {INT_MIN, 0});
        colMarked.resize(n, {INT_MIN, 0});
        res.resize(m, vector<int>(n, 0));
        for(int i = 0; i < m; i ++){
            for(int j = 0; j < n; j ++){
                pq.push({i, j, matrix[i][j]});
            }
        }
        while(!pq.empty()){
            Node cur = pq.top(); pq.pop();
            int r = cur.r, c = cur.c, val = cur.val;
            int valRow = val == rowMarked[r].first ? rowMarked[r].second : rowMarked[r].second + 1;
            int valCol = val == colMarked[c].first ? colMarked[c].second : colMarked[c].second + 1;
            res[r][c] = max(valRow, valCol);
            rowMarked[r].first = colMarked[c].first = val;
            rowMarked[r].second = colMarked[c].second = res[r][c];
        }
        return res;
    }
};

并查集+拓扑排序
详见高赞题解；
（1）先将同行同列相同元素合并；
（2）然后对每行每列的元素进行排序建边构图；
（3）最后拓扑排序计算秩；

class UnionSet{
private:
    vector<int> father;
public:
    UnionSet(int n){
        father.resize(n);
        for(int i = 0; i < n; i ++) father[i] = i;
    }

    int findFather(int x){
        if(x != father[x]) father[x] = findFather(father[x]);
        return father[x];
    }

    bool merge(int x, int y){
        int fa = findFather(x);
        int fb = findFather(y);
        
        if(fa != fb){
            father[fa] = fb;
            return true;
        }
        return false;
    }
};
class Solution {
public:
    vector<vector<int>> matrixRankTransform(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();

        vector<vector<int>> res(m, vector<int>(n));
        UnionSet ust(m * n); // 并查集

        // 将每行相同元素合并
        for(int i = 0; i < m; i ++){
            unordered_map<int, vector<int>> ump;
            for(int j = 0; j < n; j ++){
                ump[matrix[i][j]].push_back(j);
            }
            for(auto& [val, vec]:ump){
                for(int k = 0; k + 1 < vec.size(); k ++){ // 只需要相邻元素合并即可
                    ust.merge(i * n + vec[k], i * n + vec[k + 1]);
                }
            }
        }

        // 将每列相同元素合并
        for(int j = 0; j < n; j ++){
            unordered_map<int, vector<int>> ump;
            for(int i = 0; i < m; i ++){
                ump[matrix[i][j]].push_back(i);
            }
            for(auto& [val, vec]:ump){
                for(int k = 0; k + 1 < vec.size(); k ++){
                    ust.merge(vec[k] * n + j, vec[k + 1] * n + j);
                }
            }
        }

        // 构图
        vector<vector<int>> Adj(m * n);
        vector<int> inDegree(m * n, 0);

        // 每行进行排序和连边
        for(int i = 0; i < m; i ++){
            vector<pair<int, int>> vec; // 按照val排序，然后根据坐标连边
            for(int j = 0; j < n; j ++){
                vec.push_back({matrix[i][j], j});
            }
            sort(vec.begin(), vec.end());
            for(int k = 0; k + 1 < vec.size(); k ++){
                if(vec[k].first != vec[k + 1].first){
                    int u = ust.findFather(i * n + vec[k].second);
                    int v = ust.findFather(i * n + vec[k + 1].second);
                    Adj[u].push_back(v);
                    inDegree[v] ++;
                }
            }
        }

        // 每列进行排序和连边
        for(int j = 0; j < n; j ++){
            vector<pair<int, int>> vec;
            for(int i = 0; i < m; i ++){
                vec.push_back({matrix[i][j], i});
            }
            sort(vec.begin(), vec.end());
            for(int k = 0; k + 1 < vec.size(); k ++){
                if(vec[k].first != vec[k + 1].first){
                    int u = ust.findFather(vec[k].second * n + j);
                    int v = ust.findFather(vec[k + 1].second * n + j);
                    Adj[u].push_back(v);
                    inDegree[v] ++;
                }
            }
        }

        // 拓扑排序
        queue<int> q;
        vector<int> ans(m * n, 1); // 记录每个集合根位置的秩
        for(int u = 0; u < m * n; u ++){
            if(u == ust.findFather(u) && inDegree[u] == 0) q.push(u);
        }
        while(!q.empty()){
            int u = q.front(); q.pop();
            for(int v:Adj[u]){
                inDegree[v] --;
                ans[v] = max(ans[v], ans[u] + 1);
                if(inDegree[v] == 0){
                    q.push(v);
                }
            }
        }

        // 根据集合根元素的秩还原矩阵元素的秩
        for(int i = 0; i < m; i ++){
            for(int j = 0; j < n; j ++){
                int u = i * n + j;
                res[i][j] = ans[ust.findFather(u)];
            }
        }
        return res;
    }
};

1591. 奇怪的打印机 II

Description
给你一个奇怪的打印机，它有如下两个特殊的打印规则：

每一次操作时，打印机会用同一种颜色打印一个矩形的形状，每次打印会覆盖矩形对应格子里原本的颜色。
一旦矩形根据上面的规则使用了一种颜色，那么 相同的颜色不能再被使用 。
给你一个初始没有颜色的 m x n 的矩形 targetGrid ，其中 targetGrid[row][col] 是位置 (row, col) 的颜色。

如果你能按照上述规则打印出矩形 targetGrid ，请你返回 true ，否则返回 false 。

Example
示例 1：
输入：targetGrid = [[1,1,1,1],[1,2,2,1],[1,2,2,1],[1,1,1,1]]
输出：true

示例 2：
输入：targetGrid = [[1,1,1,1],[1,1,3,3],[1,1,3,4],[5,5,1,4]]
输出：true

示例 3：
输入：targetGrid = [[1,2,1],[2,1,2],[1,2,1]]
输出：false
解释：没有办法得到 targetGrid ，因为每一轮操作使用的颜色互不相同。

示例 4：
输入：targetGrid = [[1,1,1],[3,1,3]]
输出：false

提示：
m == targetGrid.length
n == targetGrid[i].length
1 <= m, n <= 60
1 <= targetGrid[row][col] <= 60

Program
拓扑排序
详见高赞题解。
思路如下：
首先，题目需要确认一个涂色顺序，使得最终结果为给定矩阵；
其次，如果一种颜色v的格子落在另一种颜色u的矩形内，那么说明u先于v涂色，u -> v有边相连；
最后，判断是否能够形成拓扑排序。
具体步骤：
（1）遍历每个格子的颜色，判断每种颜色的上下左右矩形边界；
（2）根据每个格子是否在其他颜色矩形内构图；
（3）拓扑排序判断是否无环。

class Solution {
private:
    vector<int> Adj[61]; //邻接表
    int margin[4][61]; //0, 1, 2, 3,分别对应矩形上下左右边
    bool isConnect[61][61]; //是否已经连边
    int inDegree[61];
public:
    bool isPrintable(vector<vector<int>>& targetGrid) {
        int m = targetGrid.size(), n = targetGrid[0].size();
        memset(margin, -1, sizeof(margin));
        memset(isConnect, false, sizeof(isConnect));
        memset(inDegree, 0, sizeof(inDegree));

        // 计算每个颜色矩形的上下左右边界
        for(int i = 0; i < m; i ++){
            for(int j = 0; j < n; j ++){
                int curColor = targetGrid[i][j];
                margin[0][curColor] = margin[0][curColor] == -1 ? i : min(margin[0][curColor], i);
                margin[1][curColor] = margin[1][curColor] == -1 ? i : max(margin[1][curColor], i);
                margin[2][curColor] = margin[2][curColor] == -1 ? j : min(margin[2][curColor], j);
                margin[3][curColor] = margin[3][curColor] == -1 ? j : max(margin[3][curColor], j);
            }
        }

        // 构图，如果一种颜色v的格子落在另一种颜色u的矩形内，那么说明u先于v涂色，u -> v有边相连；
        for(int i = 0; i < m; i ++){
            for(int j = 0; j < n; j ++){
                int curColor = targetGrid[i][j];
                for(int color = 1; color <= 60; color ++){
                    if(color != curColor && !isConnect[color][curColor]
                    && margin[0][color] <= i && i <= margin[1][color]
                    && margin[2][color] <= j && j <= margin[3][color]){
                        isConnect[color][curColor] = true;
                        Adj[color].push_back(curColor);
                        inDegree[curColor] ++;
                    }
                }
            }
        }

        queue<int> q;
        for(int color = 0; color <= 60; color ++){
            if(inDegree[color] == 0){
                q.push(color);
            }
        }

        while(!q.empty()){
            int u = q.front(); q.pop();
            for(int v:Adj[u]){
                inDegree[v] --;
                if(inDegree[v] == 0){
                    q.push(v);
                }
            }
        }

        int ans = 0;
        for(int color = 1; color <= 60; color ++) ans += inDegree[color] == 0 ? 1 : 0;
        return ans == 60;
    }
};

关键路径

顶点活动（Activity On Vertec, AOV）网是指用顶点表示活动，而用边集表示活动间优先关系的有向图。
边活动（Activity On Edge, AOE）网是指用带权的边集表示活动，而用顶点表示事件的有向图，其中边权表示完成活动需要的事件。
AOE网中的最长路径被称为关键路径，而关键路径上的活动称为关键活动
活动Ar的最早开始时间和最晚开始时间e[r]和l[r]，事件Vi的最早开始时间和最晚开始时间ve[i]和vl[i]。

• Vi–Ar–Vj
• e[r]=ve[i]
• l[r]=vl[j]-length[r]
  所以，只需要求出ve和vl这两个数组，就可以通过上面的公式得到e和l这两个数组。
  求解ve和vl：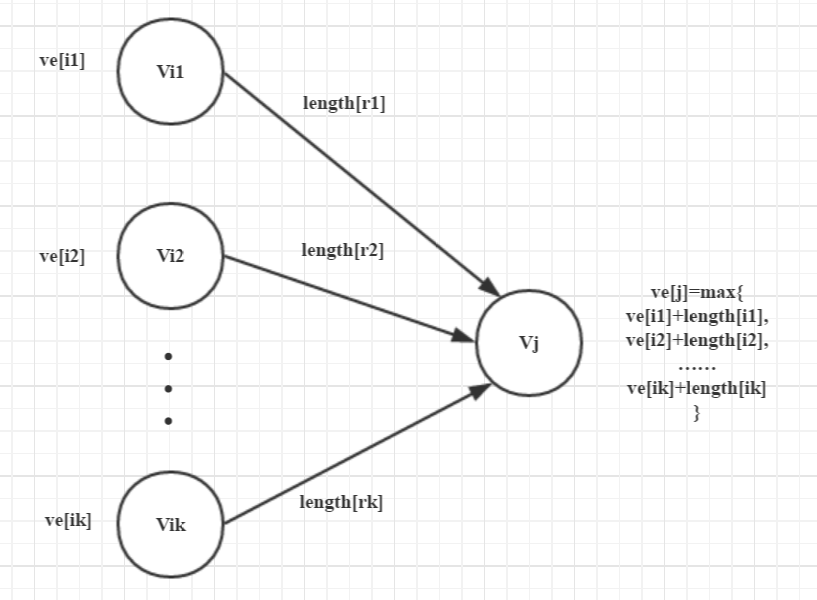
  

在访问某个节点时保证它的前驱节点都已经访问完毕
拓扑排序：

stack<int> topOrder;

//拓扑排序，顺便求ve数组
bool topologicalSort(){
  memset(ve,0,sizeof(0));
  queue<int> q;
  for(int i=0;i<n;i++){
    if(inDegree[i]==0){
      q.push(i);
    }
  }
  while(!q.empty()){
    int u=q.front();
    q.pop();
    topOrder.push(u);
    for(int i=0;i<Adj[u].size();i++){
      int v=Adj[u][i].v;
      int len=Adj[u][i].dis;
      inDegree[v]--;
      if(inDegree[v]==0) q.push[v];

      if(ve[u]+len>ve[v]){
        ve[v]=ve[u]+len;
      }
    }
  }
  if(topOrder.size()==n) return true;
  else return false;
}

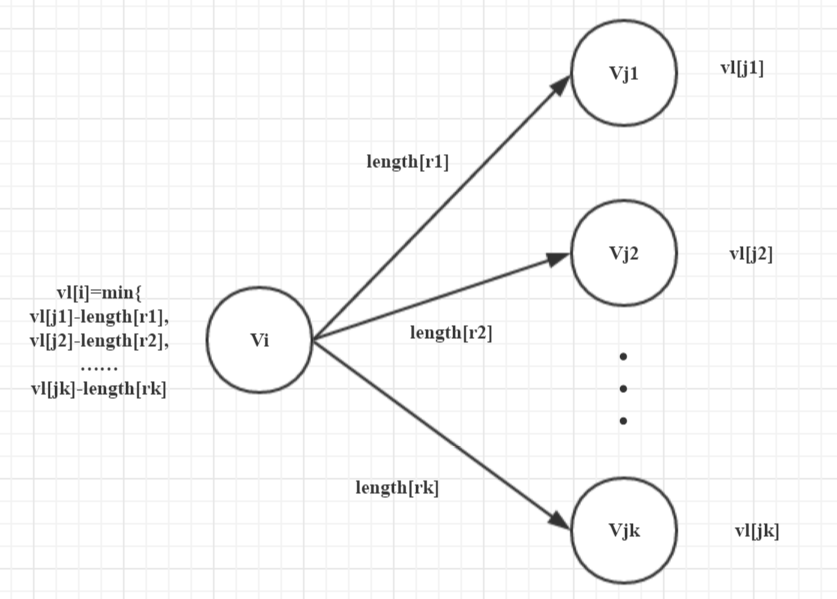
在访问某个节点时保证它的后继节点都已经访问完毕
逆拓扑排序：
汇点确定与否：
汇点不确定时，肯定ve最大的为汇点

fill(vl,vl+n,ve[n-1]); //适用于汇点确定且唯一的情况

//适用于汇点不确定
int maxLen=0;
for(int i=0;i<n;i++){
  if(ve[i]>maxLen) maxLen=ve[i];
}
fill(vl,vl+n,maxLen);

int CriticalPath(){
  memset(ve,0,sizeof(ve));
  //拓扑排序求事件最早开始时间ve
  if(!topologicalSort()) return -1; //不是有向无环图

  int maxLen=0;
  for(int i=0;i<n;i++){
    if(ve[i]>maxLen) maxLen=ve[i];
  }
  fill(vl,vl+n,maxLen);

  //逆拓扑排序求事件最晚开始时间vl
  while(!topOrder.empty()){
    int u=topOrder.top();
    topOrder.pop();
    for(int i=0;i<Adj[u].size();i++){
      int v=Adj[u][i].v;
      int len=Adj[u][i].dis;
      if(vl[v]-len<vl[u]){
        vl[u]=vl[v]-len;
      }
    }
  }

  //遍历所有边，求关键活动
  for(int u=0;u<n;u++){
    for(int i=0;i<Adj[u].size();i++){
      int v=Adj[u][i].v;
      int len=Adj[u][i].dis;
      int e=ve[u],l=vl[v]-len;
      if(e==l) cout<<"u->v"<<endl;
    }
  }
  return maxLen; //返回关键路径长度
}

注意：如果需要输出最短路径，则构建邻接表进行DFS！

关键路径

题目描述
图的连接边上的数据表示其权值，带权值的图称作网。
上图可描述为顶点集为（a,b,c,d,e)
边集及其权值为(始点，终点 权值）：
a b 3
a c 2
b d 5
c d 7
c e 4
d e 6
网的源点是入度为0的顶点，汇点是出度为0的顶点。网的关键路径是指从源点到汇点的所有路径中，具有最大路径长度的路径。上图中的关键路径为a->c->d->e，其权值之和为关键路径的长度为15。
本题的要求是根据给出的网的邻接矩阵求该网的关键路径及其长度。
输入
第一行输入一个正整数n（1<=n<=5)，其代表测试数据数目，即图的数目
第二行输入x(1<=x<=15)代表顶点个数，y(1<=y<=19)代表边的条数
第三行给出图中的顶点集，共x个小写字母表示顶点
接下来每行给出一条边的始点和终点及其权值，用空格相隔，每行代表一条边。
输出
第一个输出是图的关键路径（用给出的字母表示顶点， 用括号将边括起来，顶点逗号相隔）
第二个输出是关键路径的长度
每个矩阵对应上面两个输出，两个输出在同一行用空格间隔，每个矩阵的输出占一行。
样例输入
2
5 6
abcde
a b 3
a c 2
b d 5
c d 7
c e 4
d e 6
4 5
abcd
a b 2
a c 3
a d 4
b d 1
c d 3
样例输出
(a,c) (c,d) (d,e) 15
(a,c) (c,d) 6
程序

//题目有问题，始终50%
#include<iostream>
#include<cstring>
#include<algorithm>
#include<stack>
#include<queue>
#include<map>
#include<vector>
using namespace std;
const int MAXV=20;
const int INF=0x3f3f3f3f;
int G[MAXV][MAXV];
int n,x,y;
map<char,int> cToi;
map<int,char> iToc;
int inDegree[MAXV];
int ve[MAXV],vl[MAXV];
vector< vector<int> > Adj;

vector<int> vEnds; //汇点
vector<int> path;

stack<int> topOrder;
bool topologicalSort(){
	memset(ve,0,sizeof(ve));
	queue<int> q;

	for(int i=0;i<x;i++){
		if(inDegree[i]==0){
			q.push(i);
		}
	}
	while(!topOrder.empty()) topOrder.pop();
	while(!q.empty()){
		int u=q.front();
		q.pop();
		topOrder.push(u);
		for(int v=0;v<x;v++){
			inDegree[v]--;
			if(inDegree[v]==0) q.push(v);
			if(G[u][v]!=INF&&ve[u]+G[u][v]>ve[v]){
				ve[v]=ve[u]+G[u][v];
			}
		}
	}

	if(topOrder.size()!=x) return false;
	return true;
}
int CriticalPath(){

	if(!topologicalSort()) return -1;

	int maxLen=0;
	for(int i=0;i<x;i++){
		if(ve[i]>maxLen){
			maxLen=ve[i];
		}
	}

	fill(vl,vl+x,maxLen);
	while(!topOrder.empty()){
		int u=topOrder.top();
		topOrder.pop();
		for(int v=0;v<x;v++){
			if(G[u][v]!=INF){
				int len=G[u][v];
				if(vl[v]-len<vl[u]){
					vl[u]=vl[v]-len;
				}
			}
		}
	}

	Adj.clear();
	Adj.resize(x);
	for(int u=0;u<x;u++){
		for(int v=0;v<x;v++){
			if(G[u][v]!=INF){
				int e=ve[u],l=vl[v]-G[u][v];
				if(e==l){
					Adj[v].push_back(u);
				}
			}
		}
	}
	vEnds.clear();
	for(int i=0;i<x;i++){
		if(ve[i]==maxLen) vEnds.push_back(i);
	}
	return maxLen;
}

void DFS(int u){
	int i;
	for(i=0;i<Adj[u].size();i++){
		int v=Adj[u][i];
		path.push_back(v);
		DFS(v);
		path.pop_back();
	}
	if(i==0){
		vector<int> tmpPath=path;
		reverse(tmpPath.begin(),tmpPath.end());
		for(int i=0;i<tmpPath.size()-1;i++){
			int a=tmpPath[i],b=tmpPath[i+1];
			cout<<"("<<iToc[a]<<","<<iToc[b]<<") ";
		}
	}
}
void printPath(){
	path.clear();
	for(int i=0;i<vEnds.size();i++){
		path.push_back(vEnds[i]);
		DFS(vEnds[i]);
		path.pop_back();
	}
}
int main(){
	cin>>n;
	while(n--){
		cin>>x>>y;
		cToi.clear();
		iToc.clear();
		memset(G,INF,sizeof(G));
		memset(inDegree,0,sizeof(inDegree));
		for(int i=0;i<x;i++){
			char c;
			cin>>c;
			cToi[c]=i;
			iToc[i]=c;
		}
		for(int i=0;i<y;i++){
			char a,b;
			int l;
			cin>>a>>b>>l;
			G[cToi[a]][cToi[b]]=l;
			inDegree[cToi[b]]++;
		}
		if(x==1){
			cout<<"("<<iToc[0]<<","<<iToc[0]<<") 0"<<endl;
		}else{
			int len=CriticalPath();
			printPath();
			cout<<len<<endl;
		}

	}
	return 0;
}

二叉树

动态实现

二叉树的存储结构

typedef int TypeName;
struct Node{
  TypeName data;
  Node* lchild;
  Node* rchild;
}

新建节点

Node* newNode(TypeName v){
  Node* node=new Node;
  node->data=v;
  node->lchild=node->rchild=NULL;
  return node;
}

二叉树节点的查找、修改

void search(Node *root,TypeName x, TypeName newData){
  if(root==NULL) return;
  if(root->data==x){
    root->data=newData;
  }
  search(root->lchild,x,newData);
  search(root->rchild,x,newData);
}

二叉树节点的插入

void insert(Node* &root, TypeNmae x){
  if(root==NULL){
    root=newNode(x);
    return;
  }
  if(由二叉树的性质，x应该插在左子树){
    insert(root->lchild,x);
  }
  else{
    insert(root->richld,x);
  }
}

二叉树的创建

Node* create(TypeName data[], int n){
  Node* root=NULL;
  for(int i=0;i<n;i++){
    insert(roor,data[i]);
  }
  return root;
}

先序遍历

void preOrder(Node* root){
  if(root==NULL){
    return;
  }
  cout<<root->data;
  preOrder(root->lchild);
  preOrder(root->rchild);
}

中序遍历

void inOrder(Node* root){
  if(root==NULL){
    return;
  }
  inOrder(root->lchild);
  cout<<root->data;
  inOrder(root->rchild);
}

后序遍历

void postOrder(Node* root){
  if(root==NULL){
    return;
  }
  postOrder(root->lchild);
  postOrder(root->rchild);
  cout<<root->data;
}

先、中、后续遍历非递归实现

struct BiTree{
	int val;
	BiTree *left, *right;
};

void preOrder(BiTree* root){
	BiTree* p=root;
	stack<BiTree*> st;
	while(p!=NULL||!st.empty()){
		while(p!=NULL){
			cout<<p->val<<endl;
			st.push(p);
			p=p->left;
		}
		if(!st.empty()){
			p=st.top();st.pop();
			p=p->right;
		}
	}
}
void inOrder(BiTree* root){
	BiTree* p=root;
	stack<BiTree*> st;
	while(p!=NULL||!st.empty()){
		while(p!=NULL){
			st.push(p);
			p=p->left;
		}
		if(!st.empty()){
			p=st.top();st.pop();
			cout<<p->val<<endl;
			p=p->right;
		}
	}
}
void lastOrder(BiTree* root){
	BiTree* p=root, pre=NULL;
	stack<BiTree*> st;
	while(p!=NULL||!st.empty()){
		while(p!=NULL){
			st.push(p);
			p=p->left;
		}
		if(!st.empty()){
			p=st.top();
			if(p->right!=NULL&&pre!=p->right){
				p=p->right;
			}else{
				cout<<p->val<<endl;
				st.pop();
				pre=p;
				p=NULL;
			}
		}
	}
}

层序遍历

void layerOrder(Node* root){
  if(root==NULL) return;
  queue<Node*> q;
  q.push(root);
  while(!q.empty()){
    Node* now=q.front();
    q.pop();
    cout<<now->data;
    if(now->lchild!=NULL) q.push(now->lchild);
    if(now->rchild!=NULL) q.push(now->rchild);
  }
}

计算每个节点所处层次

typedef int TypeName;
strcut Node{
  TypeName data;
  int layer;
  Node* lchild;
  Node* rchild;
}
void layerOder(Node* root){
  if(root==NULL) return;
  queue<Node*> q;
  root->layer=1;
  q.push(root);
  while(!q.empty()){
    Node* now=q.front();
    q.pop();
    if(now->lchild!=NULL){
      now->lchild->layer=now->layer+1;
      q.push(now->lchild);
    }
    if(now->rchild!=NULL){
      now->rchild->layer=now->layer+1;
      q.push(now->rchild);
    }
  }
}

先序中序建树

typedef int TypeName;
const int MAX=100;
TypeName pre[MAX];
TypeName in[MAX];
Node* create(int preL,int preR, int inL,int inR){
  if(preL>preR||inL>inR) return NULL;
  Node* root=new Node;
  root->data=pre[preL];
  //线性查找，当然可以二分查找
  int k;
  for(k=inL;k<=inR;k++){
    if(pre[preL]==in[k]) break;
  }
  int numLeft=k-inL;
  root->lchild=create(preL+1,preL+numLeft,inL,k-1);
  root->rchild=create(preL+numLeft+1,preR,k+1,inR);
  return root;
}

中序后序建树

typedef int TypeName;
const int MAX=100;
TypeName in[MAX];
TypeName post[MAX];
Node* create(int inL,int inR, int pL,int pR){
  if(inL>inR||pL>pR) return NULL;
  Node* root=new Node;
  root->data=post[pR];
  int k;
  for(k=inL;k<=inR;k++){
    if(post[pR]==in[k]) break;
  }
  int numLeft=k-inL;
  root->lchild=create(inL,k-1,pL,pL+numLeft-1);
  root->rchild=create(k+1,inR,pl+numLeft,pR);
  return root;
}

中序层序建树

typedef int TypeName;
vector<TypeNmae> layer;
vector<TypeName> in;
Node* create(vector<TypeName> layer,vector<TypeName> in,int inL,int inR){
  if(layer.size()==0||inL>inR) return NULL;
  Node* root=new Node;
  root->data=layer[0];
  int pos;
  for(pos=0;pos<in.size();pos++){
    if(layer[0]==in[pos]) break;
  }
  vector<TypeName> leftLayer,rightLayer;
  vector<TypeName> leftIn,rightIn;
  for(int i=1;i<layer.size();i++){
    int j;
    for(j=0;j<pos;j++){
      if(layer[i]==in[j]){
        leftLayer.push_back(layer[i]);
        break;
      }
    }
    if(j==pos) rightLayer.push_back(layer[i]);
  }
  root->lchild=create(leftLayer,in,inL,pos-1);
  root->rchild=create(rightLayer,in,pos+1,inR);
  return root;
}

静态实现

存储结构

typedef int TypeName;
struct Node{
  TypeName data;
  int lchild;
  int rchild;
}BinaryTree[MAX];

新建节点

int index=0;
int newNode(int v){
  BianryTree[index].data=v;
  BianryTree[index].lchild=-1;
  BinaryTree[index].rchild=-1;
  return index++;
}

查找

void search(int root,int x,int newData){
  if(root==-1) return;
  if(BinaryTree[root].data==x) BinaryTree[root].data=newData;
  search(BinaryTree[root].lchild,x,newData);
  search(BinaryTree[root].rchild,x,newData);
}

插入

void insert(int &root,int x){
  if(root==-1){
    root=newNode(x);
    return;
  }
  if(由二叉树的性质x应该插在左子树){
    insert(BinaryTree[root].lchild,x);
  }else{
    insert(BInaryTree[root].rcchild,x);
  }
}

建树

int Create(int data[],int n){
  int root=-1;
  for(int i=0;i<n;i++){
    insert(root,data[i]);
  }
  return root;
}

遍历

void preOrder(int root){
  if(root==-1) return;
  cout<<BinaryTree[root].data;
  preOrder(BianryTree[root].lchild);
  preOrder(BinaryTree[root].rchild);
}

void inOrder(int root){
  if(root==-1) return;
  inOrder(BinaryTree[root].lchild);
  cout<<BInaryTree[root].data;
  inOrder(BInaryTree[root].rchild);
}

void postOrder(int root){
  if(root==-1) return;
  postOrder(BianryTree[root].lchild);
  postOrder(BinaryTree[root].rchild);
  cout<<BInaryTree[root].data;
}

void levelOrder(int root){
  if(root==-1) return;
  queue<int> q;
  q.push(root);
  while(!q.empty()){
    int now=q.front();
    q.pop();
    cout<<BinaryTree[root].data;
    if(BinaryTree[root].lchild!=-1) q.push(BinaryTree[root].lchild);
    if(BinaryTree[root].rchild!=-1) q.push(BinaryTree[root].rchild);
  }
}

PAT-A1020 Tree Traversals

Description
Suppose that all the keys in a binary tree are distinct positive integers. Given the postorder and inorder traversal sequences, you are supposed to output the level order traversal sequence of the corresponding binary tree.
Input Specification
Each input file contains one test case. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the postorder sequence and the third line gives the inorder sequence. All the numbers in a line are separated by a space.
Output Specification
For each test case, print in one line the level order traversal sequence of the corresponding binary tree. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the end of the line.
Sample Input
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
Sample Output
4 1 6 3 5 7 2
Procedure

#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;

struct Node{
	int data;
	Node* lchild;
	Node* rchild;
};
int n;
vector<int> postOrder;
vector<int> inOrder;

Node* create(int inL,int inR,int pL,int pR){
	if(inL>inR||pL>pR) return NULL;
	Node* root=new Node;
	root->data=postOrder[pR];
	int pos;
	for(pos=inL;pos<=inR;pos++){
		if(postOrder[pR]==inOrder[pos]) break;
	}
	int numLeft=pos-inL;
	root->lchild=create(inL,pos-1,pL,pL+numLeft-1);
	root->rchild=create(pos+1,inR,pL+numLeft,pR-1);
	return root;
}
void print(Node* root){
	queue<Node*> Q;
	if(root!=NULL) Q.push(root);
	bool bFirst=true;
	while(!Q.empty()){
		Node* front=Q.front();
		if(bFirst){
			bFirst=false;
		}else{
			cout<<" ";
		}
		cout<<front->data;
		Q.pop();
		if(front->lchild!=NULL) Q.push(front->lchild);
		if(front->rchild!=NULL) Q.push(front->rchild);
	}
}
int main(){
	while(cin>>n){
		postOrder.clear();
		inOrder.clear();
		for(int i=0;i<n;i++){
			int tmp;
			cin>>tmp;
			postOrder.push_back(tmp);
		}
		for(int i=0;i<n;i++){
			int tmp;
			cin>>tmp;
			inOrder.push_back(tmp);
		}
		Node* root=create(0,n-1,0,n-1);
		print(root);
	}
	return 0;
}

复原二叉树

题目描述
小明在做数据结构的作业，其中一题是给你一棵二叉树的前序遍历和中序遍历结果，要求你写出这棵二叉树的后序遍历结果。
输入
输入包含多组测试数据。每组输入包含两个字符串，分别表示二叉树的前序遍历和中序遍历结果。每个字符串由不重复的大写字母组成。
输出
对于每组输入，输出对应的二叉树的后续遍历结果。
样例输入
DBACEGF ABCDEFG
BCAD CBAD
样例输出
ACBFGED
CDAB
程序

#include<iostream>
#include<cstring>
using namespace std;
struct Node{
	char data;
	Node* lchild;
	Node* rchild;
};
string preOrder;
string inOrder;
Node* create(int inL,int inR,int preL,int preR){
	if(inL>inR||preL>preR) return NULL;
	Node* root=new Node;
	root->data=preOrder[preL];
	int pos;
	for(pos=inL;pos<=inR;pos++){
		if(preOrder[preL]==inOrder[pos])break;
	}
	int numLeft=pos-inL;
	root->lchild=create(inL,pos-1,preL+1,preL+numLeft);
	root->rchild=create(pos+1,inR,preL+numLeft+1,preR);
	return root;
}
void postOrder(Node* root){
	if(root==NULL) return;
	postOrder(root->lchild);
	postOrder(root->rchild);
	cout<<root->data;
}
int main(){
	while(cin>>preOrder>>inOrder){
		Node* root=create(0,preOrder.size()-1,0,inOrder.size()-1);
		postOrder(root);
		cout<<endl;
	}
	return 0;
}

二叉树

题目描述
如上所示，由正整数1，2，3……组成了一颗特殊二叉树。我们已知这个二叉树的最后一个结点是n。现在的问题是，结点m所在的子树中一共包括多少个结点。
比如，n = 12，m = 3那么上图中的结点13，14，15以及后面的结点都是不存在的，结点m所在子树中包括的结点有3，6，7，12，因此结点m的所在子树中共有4个结点。
输入
输入数据包括多行，每行给出一组测试数据，包括两个整数m，n (1 <= m <= n <= 1000000000)。最后一组测试数据中包括两个0，表示输入的结束，这组数据不用处理。
输出
对于每一组测试数据，输出一行，该行包含一个整数，给出结点m所在子树中包括的结点的数目。
样例输入
3 7
142 6574
2 754
0 0
样例输出
3
63
498
程序

#include<iostream>
#include<cmath>
using namespace std;

int m,n;

int main(){
	while(cin>>m>>n&&m!=0){

		int nCount=0;
		int treeH=ceil(log2(n+1));
		int subH=ceil(log2(m+1));
		nCount=pow(2,treeH-subH)-1; //最后一层未计算
		int h=treeH-subH;
		int l,r;
		l=r=m;
		while(h!=0){
			l*=2;
			r=r*2+1;
			h--;
		}
		if(r<=n){
			nCount+=r-l+1;
		}else if(l<=n){
			nCount+=n-l+1;
		}
		cout<<nCount<<endl;
	}
	return 0;
}

树的遍历

存储结构

typedef int TypeName;
struct Node{
  TypeNmae data;
  vector<int> child;
}Tree[MAX];

新建节点

int index=0;
int newNode(TypeName v){
  Tree[index].data=v;
  Tree[index].child.clear();
  return index++;
}

先根遍历

void preOrder(int root){
  cout<<Tree[root].data;
  for(int i=0;i<Tree[root].child.size();i++){
    preOrder(Tree[root].child[i]);
  }
}

层序遍历

void layerOrder(int root){
  queue<int> Q;
  Q.push(root);
  while(!Q.empty()){
    int front=Q.front();
    cout<<Tree[front].data;
    Q.pop();
    for(int i=0;i<Tree[front].child.size();i++){
      Q.push(Tree[front].child[i]);
    }
  }
}

层序编号

struct Node{
  int layer;
  TypeName data;
  vector<int> child;
}Tree[MAX];
void layerOrder(int root){
  queue<int> Q;
  Q.push(root);
  Tree[root].layer=0;
  while(!Q.empty()){
    int front=Q.front();
    cout<<Tree[front].data;
    Q.pop();
    for(int i=0;i<Tree[front].child.size();i++){
      int childIndex=Tree[front].child[i];
      Tree[childIndex].layer=Tree[front].layer+1;
      Q.push(childIndex);
    }
  }
}

Pat-A1053 Path of Equal Weight

Description
Given a non-empty tree with root R, and with weight Wi assigned to each tree node Ti. The weight of a path from R to L is defined to be the sum of the weights of all the nodes along the path from R to any leaf node L. Now given any weighted tree, you are supposed to find all the paths with their weights equal to a given number. For example, let’s consider the tree showed in the following figure: for each node, the upper number is the node ID which is a two-digit number, and the lower number is the weight of that node. Suppose that the given number is 24, then there exists 4 different paths which have the same given weight: {10 5 2 7}, {10 4 10}, {10 3 3 6 2} and {10 3 3 6 2}, which correspond to the red edges in the figure.

Input Specification
Each input file contains one test case. Each case starts with a line containing 0<N≤100, the number of nodes in a tree, M (<N), the number of non-leaf nodes, and 0<S<$2^{30}$, the given weight number. The next line contains N positive numbers where W​i(<1000) corresponds to the tree node Ti. Then M lines follow, each in the format:
ID K ID[1] ID[2] … ID[K]
where ID is a two-digit number representing a given non-leaf node, K is the number of its children, followed by a sequence of two-digit ID’s of its children. For the sake of simplicity, let us fix the root ID to be 00.
Output Specification
For each test case, print all the paths with weight S in non-increasing order. Each path occupies a line with printed weights from the root to the leaf in order. All the numbers must be separated by a space with no extra space at the end of the line.
Note: sequence {A1,A2,⋯,An} is said to be greater than sequence {B1,B2,⋯,B​m} if there exists 1≤k<min{n,m} such that Ai=Bi for i=1,⋯,k, and Ak+1>Bk+1.
Sample Input
20 9 24
10 2 4 3 5 10 2 18 9 7 2 2 1 3 12 1 8 6 2 2
00 4 01 02 03 04
02 1 05
04 2 06 07
03 3 11 12 13
06 1 09
07 2 08 10
16 1 15
13 3 14 16 17
17 2 18 19
Sample Output
10 5 2 7
10 4 10
10 3 3 6 2
10 3 3 6 2
Procedure

#include<iostream>
#include<vector>
#include<algorithm>
#include<functional>
using namespace std;
const int MAXN=101;
struct Node{
	int weight;
	vector<int> child;
}Tree[MAXN];
bool cmp(int a,int b){
	return Tree[a].weight>Tree[b].weight;
}
int n,m,s;
vector<int> path;
void DFS(int index,int sum){
	if(sum>s) return;  //不符合题意
	if(sum==s){
		if(!Tree[index].child.empty()) return; //非叶子节点
		for(int i=0;i<path.size();i++){
			if(i!=0) cout<<" ";
			cout<<Tree[path[i]].weight;
		}
		cout<<endl;
		return;
	}
	for(int i=0;i<Tree[index].child.size();i++){
		int childIndex=Tree[index].child[i];
		path.push_back(childIndex);
		DFS(childIndex,sum+Tree[childIndex].weight);
		path.pop_back();
	}
}
int main(){
	cin>>n>>m>>s;
	for(int i=0;i<n;i++) cin>>Tree[i].weight;
	for(int i=0;i<m;i++){
		int id,k;
		cin>>id>>k;
		for(int j=0;j<k;j++){
			int child;
			cin>>child;
			Tree[id].child.push_back(child);
		}
		sort(Tree[id].child.begin(),Tree[id].child.end(),cmp);
	}
	path.push_back(0);
	DFS(0,Tree[0].weight);
	return 0;
}

树查找

题目描述
有一棵树，输出某一深度的所有节点，有则输出这些节点，无则输出EMPTY。该树是完全二叉树。
输入
输入有多组数据。
每组输入一个n(1<=n<=1000)，然后将树中的这n个节点依次输入，再输入一个d代表深度。
输出
输出该树中第d层得所有节点，节点间用空格隔开，最后一个节点后没有空格。
样例输入
5
1 2 3 4 5
7
7
1 2 3 4 5 6 7
2
0
样例输出
EMPTY
2 3
程序

#include<iostream>
#include<vector>
#include<cmath>
#include<algorithm>
using namespace std;
const int MAXN=1001;
vector<int> nodes;
int n,h;

int main(){
	while(cin>>n&&n!=0){
		nodes.clear();
		nodes.resize(n);
		for(int i=0;i<n;i++) cin>>nodes[i];
		cin>>h;
		int nowH=ceil(log2(n+1));
		int numTop=pow(2,h-1)-1;
		int numLev=pow(2,h-1);
		if(h>nowH) cout<<"EMPTY"<<endl;
		else{
			for(int i=numTop;i<n&&i<numTop+numLev;i++){
				if(i!=numTop) cout<<" ";
				cout<<nodes[i];
			}
			cout<<endl;
		}
	}
	return 0;
}

树的高度

题目描述
一棵树有n个节点，其中1号节点为根节点。
输入
第一行是整数n，表示节点数
后面若干行，每行两个整数a b，表示b是a的子节点。
输出
求这棵树的高度（根节点为第1层）
样例输入
5
1 2
1 3
3 4
3 5
样例输出
3
程序

#include<iostream>
#include<algorithm>
#include<vector>
#include<cmath>
using namespace std;
const int MAXN=1001;
struct Node{
	vector<int> child;
}Tree[MAXN];

int n;

int calLevel(int root){
	if(Tree[root].child.empty()) return 1;
	int maxLevel=0;
	for(int i=0;i<Tree[root].child.size();i++){
		int childIndex=Tree[root].child[i];
		maxLevel=max(maxLevel,calLevel(childIndex)+1);
	}
	return maxLevel;
}
int main(){
	while(cin>>n){

		int a,b;
		while(cin>>a>>b){
			Tree[a].child.push_back(b);
		}
		cout<<calLevel(1)<<endl;
	}
	return 0;
}

二叉查找树

查找

bool search(Node* root,int x){
	if(root==NULL) return false;
	if(root->data==x) return true;
	else if(x<root->data) return search(root->lchild,x);
	else return search(root->rchild,x);
}

插入操作

void insert(Node* &root,int x){
  if(root==NULL){
    root=newNode(x);
    return;
  }
  if(x==root->data){
    return;
  }else if(x<root->data){
    insert(root->lchild,x);
  }else{
    insert(root->rchild,x);
  }
}

建树

Node* create(int data[],int n){
  Node* root=NULL;
  for(int i=0;i<n;i++){
    insert(root,data[i]);
  }
  return root;
}

删除

//寻找前驱
Node* findPre(Node* root){
  while(root->rchild!=NULL){
    root=root->rchild;
  }
  return root;
}
//寻找后继
Node* findNext(Node* root){
  while(root->lchild!=NULL){
    root=root->lchild;
  }
  return root;
}
//删除节点
void deleteNode(Node* &root,int x){
  if(root==NULL) return;
  if(root->data==x){
    if(root->lchild==NULL&&root->rchild==NULL){
      root=NULL;
    }else if(root->lchild!=NULL){
      Node* pre=findPre(root->lchild);
      root->data=pre->data;
      deleteNode(root->lchild,pre->data);
    }else{
      Node* next=findNext(root->rchild);
      root->data=next->data;
      deleteNode(root->rchild,next->data);
    }
  }else if(root->data>x){
    deleteNode(root->lchild,x);
  }else{
    deleteNode(root->rchild,x);
  }
}

Pat-A1043 Is It a Binary Search Tree

Description
A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

• The left subtree of a node contains only nodes with keys less than the node’s key.
• The right subtree of a node contains only nodes with keys greater than or equal to the node’s key.
• Both the left and right subtrees must also be binary search trees.
  If we swap the left and right subtrees of every node, then the resulting tree is called the Mirror Image of a BST.
  Now given a sequence of integer keys, you are supposed to tell if it is the preorder traversal sequence of a BST or the mirror image of a BST.

Input Specification
Each input file contains one test case. For each case, the first line contains a positive integer N (≤1000). Then N integer keys are given in the next line. All the numbers in a line are separated by a space.
Output Specification
For each test case, first print in a line YES if the sequence is the preorder traversal sequence of a BST or the mirror image of a BST, or NO if not. Then if the answer is YES, print in the next line the postorder traversal sequence of that tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line.
Sample Input 1
7
8 6 5 7 10 8 11
Sample Output 1
YES
5 7 6 8 11 10 8
Sample Input 2
7
8 10 11 8 6 7 5
Sample Output 2
YES
11 8 10 7 5 6 8
Sample Input 3
7
8 6 8 5 10 9 11
Sample Output 3
NO
Procedure

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
struct Node{
	int data;
	Node* lchild;
	Node* rchild;
};
vector<int> origin,pre,preMirror,post,postMirror;
int n;
void insert(Node* &root,int x){
	if(root==NULL){
		root=new Node;
		root->data=x;
		root->lchild=root->rchild=NULL;
		return;
	}
	if(x<root->data){
		insert(root->lchild,x);
	}else{
		insert(root->rchild,x);
	}
}
Node* create(){
	Node* root=NULL;
	for(int i=0;i<origin.size();i++){
		insert(root,origin[i]);
	}
	return root;
}
void preOrder(Node* root){
	if(root==NULL) return;
	pre.push_back(root->data);
	preOrder(root->lchild);
	preOrder(root->rchild);
}
void postOrder(Node* root){
	if(root==NULL) return;
	postOrder(root->lchild);
	postOrder(root->rchild);
	post.push_back(root->data);
}
void preMirrorOrder(Node* root){
	if(root==NULL) return;
	preMirror.push_back(root->data);
	preMirrorOrder(root->rchild);
	preMirrorOrder(root->lchild);
}
void postMirrorOrder(Node* root){
	if(root==NULL) return;
	postMirrorOrder(root->rchild);
	postMirrorOrder(root->lchild);
	postMirror.push_back(root->data);
}
int main(){
	cin>>n;
	origin.resize(n);
	for(int i=0;i<n;i++) cin>>origin[i];
	Node* root=create();

	preOrder(root);
	postOrder(root);
	preMirrorOrder(root);
	postMirrorOrder(root);

	if(origin==pre){
		cout<<"YES"<<endl;
		for(vector<int>::iterator it=post.begin();it!=post.end();it++){
			if(it!=post.begin()) cout<<" ";
			cout<<*it;
		}
		cout<<endl;
	}else if(origin==preMirror){
		cout<<"YES"<<endl;
		for(vector<int>::iterator it=postMirror.begin();it!=postMirror.end();it++){
			if(it!=postMirror.begin()) cout<<" ";
			cout<<*it;
		}
		cout<<endl;
	}else{
		cout<<"NO"<<endl;
	}
	return 0;
}

平衡二叉树

存储结构

struct Node{
  int weight;
  int height;
  Node *lchild,*rchild;
}

新建节点

Node* newNode(int weight){
  Node* node=new Node;
  node->weight=weight;
  node->height=1;
  node->lchild=node->rchild=NULL;
  return node;
}

获取高度

int getHeight(Node* root){
  if(root==NULL) return 0;
  return root->height;
}

计算平衡因子

int getBalancedFactor(Node* root){
  return getHeight(root->lchild)-getHeight(root->rchild);
}

更新高度

void updateHeight(Node* root){
  root->height=max(getHeight(root->lchild),getHeight(root->rchild))+1;
}

查找

bool search(Node* root, int x){
  if(root==NULL) return false;
  if(x==root->weight) return true;
  else if(x<root->weight) return search(root->lchild,x);
  else return search(root->rchild,x);
}

左旋

void leftRotation(Node* &root){
  Node* tmp=root->rchild;
  root->rchild=tmp->lchild;
  tmp->lchild=root;
  updateHeight(root);
  updateHeight(tmp);
  root=tmp;
}

右旋

void rightRotation(Node* &root){
  Node* tmp=root->lchild;
  root->lchld=tmp->rchild;
  tmp->rchild=root;
  updateHeight(root);
  updateHeight(tmp);
  root=tmp;
}

插入

void insert(Node* &root, int weight){
  if(root==NULL){
    root=newNode(weight);
    return;
  }
  if(weight<root->weight){
    insert(root->lchild,weight);
    updateHeight(root);
    if(getBalancedFactor(root)==2){
      if(getBalancedFactor(root->lchild)==1){ //LL型
        rightRotation(root);
      }else{  //LR型
        leftRotation(root->lchild);
        rightRotation(root);
      }
    }
  }else{
    insert(root->rchild,weight);
    updateHeight(root);
    if(getBalancedFactor(root)==-2){
      if(getBalancedFactor(root->rchild)==-1){ //RR型
        leftRotation(root);
      }else{  //RL型
        rightRotation(root->rchild);
        leftRotation(root);
      }
    }
  }
}

删除

void deleteNode(Node* &root, int weight){
  if(root==NULL) return;
  if(weight==root->weight){
    if(root->lchild!=NULL&&root->rchild!=NULL){
        Node* pre=findPre(root->lchild);
        root->wegiht=pre->wegiht;
        deleteNode(root->lchild, pre->weight);
        updateHeight(root);
        if(getBalancedFactor(root)==-2){
          if(getBalancedFactor(root->rchild)==1){ //RL型
            rightRotation(root->rchild);
            leftRotation(root);
          }else{ //RR型
            leftRotation(root);
          }
        }
    }else if(root->lchild==NULL&&root->rchild==NULL){
      root=NULL;
    }else if(root->lchild!=NULL){
      root->wegiht=root->lchild->weight;
      root->lchild=NULL;
    }else{
      root->weight=root->rchild->weight;
      root->rchild=NULL;
    }
  }else if(weight<root->weight){
    deletNode(root->lchild, x);
    updateHeight(root);
    if(getBalancedFactor(root)==-2){
      if(getBalancedFactor(root->rchild)==1){ //RL型
        rightRotation(root->rchild);
        leftRotation(root);
      }else{ //RR型
        leftRotation(root);
      }
    }
  }else{
    deleteNode(root->rchild, x);
    updateHeight(root);
    if(getBalancedFactor(root)==2){  
      if(getBalancedFactor(root->lchild==-1)){ //LR型
        leftRotation(root->lchild);
        rightRotation(root);
      }else{ //LL型
        rightRotation(root);
      }
    }
  }
}

AVL树建立

Node* create(int data[],int n){
  Node* root=NULL;
  for(int i=0;i<n;i++){
    insert(root,data[i]);
  }
  return root;
}

平衡二叉树的基本操作

题目描述
平衡二叉树又称AVL树，它是一种具有平衡因子的特殊二叉排序树。平衡二叉树或者是一棵空树，或者是具有以下几条性质的二叉树：
1.若它的左子树不空，则左子树上所有结点的值均小于它的根节点的值；
2.若它的右子树不空，则右子树上所有结点的值均大于它的根节点的值；
3.它的左右子树也分别为平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。
若将二叉树上结点的平衡因子定义为该结点的左子树深度减去它的右子树的深度，则平衡二叉树上的所有结点的平衡因子只可能为-1、0和1。只要二叉树上有一个结点的平衡因子的绝对值大于1，则这棵二叉树就是不平衡的。
通过平衡二叉树的性质不难得知，其插入、删除、查询都操作的时间复杂度均为O(log2n)。
维持平衡二叉树性质的操作可以被称为旋转。其中平衡二叉树的右旋处理可以描述如下：
而其左旋处理与右旋正好相反，可以描述如下：
在本题中，读入一串整数，首先利用这些整数构造一棵平衡二叉树。另外给定多次查询，利用构造出的平衡二叉树，判断每一次查询是否成功。
输入
输入的第一行包含2个正整数n和k，分别表示共有n个整数和k次查询。其中n不超过500，k同样不超过500。
第二行包含n个用空格隔开的正整数，表示n个整数。
第三行包含k个用空格隔开的正整数，表示k次查询的目标。
输出
只有1行，包含k个整数，分别表示每一次的查询结果。如果在查询中找到了对应的整数，则输出1，否则输出0。
请在每个整数后输出一个空格，并请注意行尾输出换行。
样例输入
8 3
1 3 5 7 8 9 10 15
9 2 5
样例输出
1 0 1
程序

#include<iostream>
#include<algorithm>

using namespace std;

struct Node{
	int weight;
	int height;
	Node *lchild,*rchild;
};
int n,k;
int getHeight(Node* root){
	if(root==NULL) return 0;
	return root->height;
}
void updateHeight(Node* root){
	root->height=max(getHeight(root->lchild),getHeight(root->rchild))+1;
}
int getBalancedFactor(Node* root){
	return getHeight(root->lchild)-getHeight(root->rchild);
}
void leftRotation(Node* &root){
	Node* tmp=root->rchild;
	root->rchild=tmp->lchild;
	tmp->lchild=root;
	updateHeight(root);
	updateHeight(tmp);
	root=tmp;
}
void rightRotation(Node* &root){
	Node* tmp=root->lchild;
	root->lchild=tmp->rchild;
	tmp->rchild=root;
	updateHeight(root);
	updateHeight(tmp);
	root=tmp;
}
void insert(Node* &root,int weight){
	if(root==NULL){
		root=new Node;
		root->weight=weight;
		root->height=1;
		root->lchild=root->rchild=NULL;
		return;
	}
	if(weight<root->weight){
		insert(root->lchild,weight);
		updateHeight(root);
		if(getBalancedFactor(root)==2){
			if(getBalancedFactor(root->lchild)==1){
				rightRotation(root);
			}else{
				leftRotation(root->lchild);
				rightRotation(root);
			}
		}
	}else{
		insert(root->rchild,weight);
		updateHeight(root);
		if(getBalancedFactor(root)==-2){
			if(getBalancedFactor(root->rchild)==-1){
				leftRotation(root);
			}else{
				rightRotation(root->rchild);
				leftRotation(root);
			}
		}
	}
}
bool search(Node* root, int x){
	if(root==NULL) return false;
	if(x==root->weight) return true;
	else if(x<root->weight) return search(root->lchild,x);
	else return search(root->rchild,x);
}
int main(){
	while(cin>>n>>k){
		Node* root=NULL;
		for(int i=0;i<n;i++){
			int tmp;
			cin>>tmp;
			insert(root,tmp);
		}
		for(int i=0;i<k;i++){
			int tmp;
			cin>>tmp;
			if(search(root,tmp)) cout<<1<<" ";
			else cout<<0<<" ";
		}
		cout<<endl;
	}
	return 0;
}

堆

存储结构

const int MAXN=100;
vector<int> heap;
heap.resize(101);

向下调整

void downAdjust(int low,int high){
  int i=low,j=i*2;
  while(j<=high){
    if(j<high&&heap[j+1]>heap[j]){
      j+=1;
    }
    if(heap[j]>heap[i]){
      swap(heap[i],heap[j]);
      i=j;
      j=i*2;
    }else{
      break;
    }
  }
}

建堆

void createHeap(){
  int n=heap.size()-1;
  for(int i=n/2;i>=1;i--){
    downAdjust(i,n);
  }
}

删除堆顶元素

void deleteTop(){
  int n=heap.size()-1;
  heap[1]=heap[n--];
  heap.pop_back();
  for(int i=n/2;i>=1;i--){
    downAdjust(i,n);
  }
}

向上调整

void upAdjust(int low, int high){
  int i=high, j=i/2;
  while(j>=low){
    if(heap[j]<heap[i]){
      swap(heap[i],heap[j]);
      i=j;
      j=i/2;
    }else{
      break;
    }
  }
}

插入

void insert(int x){
  heap.push_back(x);
  upAdjust(1,n+1);
}

堆排序

void heapSort(){
  createHeap();
  for(int i=n;i>1;i--){
    swap(heap[1],heap[i]);
    downAdjust(1,i-1);
  }
}

算法10-10,10-11：堆排序

题目描述
堆排序是一种利用堆结构进行排序的方法，它只需要一个记录大小的辅助空间，每个待排序的记录仅需要占用一个存储空间。
首先建立小根堆或大根堆，然后通过利用堆的性质即堆顶的元素是最小或最大值，从而依次得出每一个元素的位置。
在本题中，读入一串整数，将其使用以上描述的堆排序的方法从小到大排序，并输出。
输入
输入的第一行包含1个正整数n，表示共有n个整数需要参与排序。其中n不超过100000。
第二行包含n个用空格隔开的正整数，表示n个需要排序的整数。
输出
只有1行，包含n个整数，表示从小到大排序完毕的所有整数。
请在每个整数后输出一个空格，并请注意行尾输出换行。
样例输入
10
2 8 4 6 1 10 7 3 5 9
样例输出
1 2 3 4 5 6 7 8 9 10
程序

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
const int MAXN=100001;
vector<int> heap;
int n;
void downAdjust(int low,int high){
	int i=low,j=i*2;
	while(j<=high){
		if(j<high&&heap[j+1]>heap[j]) j++;
		if(heap[j]>heap[i]){
			swap(heap[i],heap[j]);
			i=j;
			j=i*2;
		}else{
			break;
		}
	}
}
void createHeap(){
	for(int i=n/2;i>=1;i--){
		downAdjust(i,n);
	}
}
void heapSort(){
	createHeap();
	for(int i=n;i>=1;i--){
		swap(heap[1],heap[i]);
		downAdjust(1,i-1);
	}
}
int main(){
	while(cin>>n){
		heap.clear();
		heap.resize(n+1);
		for(int i=1;i<=n;i++) cin>>heap[i];
		heapSort();
		for(int i=1;i<=n;i++) cout<<heap[i]<<" ";
		cout<<endl;
	}
	return 0;
}

序列合并

题目描述
有两个长度都为N的序列A和B，在A和B中各取一个数相加可以得到N2个和，求这N2个和中最小的N个。
输入
第一行一个正整数N（1 <= N <= 100000）。
第二行N个整数Ai，满足Ai <= Ai+1且Ai <= 109
第三行N个整数Bi，满足Bi <= Bi+1且Bi <= 109
输出
输出仅有一行，包含N个整数，从小到大输出这N个最小的和，相邻数字之间用空格隔开。
样例输入
3
2 6 6
1 4 8
样例输出
3 6 7
程序

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
vector<int> heap,heapA,heapB;
int N;
void downAdjust(vector<int> &heap,int low,int high){
	int i=low,j=i*2;
	while(j<=high){
		if(j<high&&heap[j+1]<heap[j]) j++;
		if(heap[j]<heap[i]){
			swap(heap[i],heap[j]);
			i=j;
			j=i*2;
		}else{
			break;
		}
	}
}
void createHeap(vector<int> &heap,int n){
	for(int i=n/2;i>=1;i--){
		downAdjust(heap,i,n);
	}
}
void deleteTop(vector<int> &heap,int n){
	heap[1]=heap[n];
	heap.pop_back();
	downAdjust(heap,1,n-1);
}
void heapSort(vector<int> &heap, int n){
	for(int i=n;i>n-N;i--){
		swap(heap[1],heap[i]);
		if(i!=n) cout<<" ";
		cout<<heap[i];
		downAdjust(heap,1,i-1);
	}
	cout<<endl;
}
int main(){

	while(cin>>N){
		heap.clear();
		heapA.clear();
		heapB.clear();

		heapA.resize(N+1);
		heapB.resize(N+1);
		for(int i=1;i<=N;i++) cin>>heapA[i];
		for(int i=1;i<=N;i++) cin>>heapB[i];
		heap.push_back(0);
		for(int i=1;i<=N&&i<=2;i++){
			for(int j=1;j<=N;j++){
				int tmp=heapA[i]+heapB[j];
				heap.push_back(tmp);
			}
		}

		createHeap(heap,heap.size()-1);
		heapSort(heap,heap.size()-1);

	}
	return 0;
}

合并果子（堆）

题目描述
在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。
每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过n-1次合并之后，就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为1，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。
例如有3种果子，数目依次为1，2，9。可以先将 1、2堆合并，新堆数目为3，耗费体力为3。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为12，耗费体力为 12。所以多多总共耗费体力=3+12=15。可以证明15为最小的体力耗费值。
输入
输入文件fruit.in包括两行，第一行是一个整数n（1 <= n <= 30000），表示果子的种类数。第二行包含n个整数，用空格分隔，第i个整数ai（1 <= ai <= 20000）是第i种果子的数目。
输出
输出文件fruit.out包括一行，这一行只包含一个整数，也就是最小的体力耗费值。输入数据保证这个值小于231。
样例输入
10
3 5 1 7 6 4 2 5 4 1
样例输出
120
程序

#include<iostream>
#include<functional>
#include<queue>
#include<vector>
#include<algorithm>
using namespace std;
int n;
struct myCmp{
	bool operator ()(const int &a,const int &b) const{
		return a>b;
	}
};
priority_queue<int,vector<int>,myCmp> pq;

int main(){
	while(cin>>n){
		for(int i=0;i<n;i++){
			int tmp;
			cin>>tmp;
			pq.push(tmp);
		}
		int sum=0;
		while(pq.size()!=1){
			int top=pq.top();
			pq.pop();
			top+=pq.top();
			sum+=top;
			pq.pop();
			pq.push(top);
		}
		cout<<sum<<endl;
	}
	return 0;
}

#include<iostream>
#include<functional>
#include<queue>
#include<vector>
#include<algorithm>
using namespace std;
int n;
vector<int> heap;
void downAdjust(int low,int high){
	int i=low,j=i*2;
	while(j<=high){
		if(j<high&&heap[j+1]<heap[j]) j++;
		if(heap[j]<heap[i]){
			swap(heap[i],heap[j]);
			i=j;
			j=i*2;
		}else break;
	}
}
void upAdjust(int low,int high){
	int i=high,j=i/2;
	while(i>=low){
		if(heap[i]<heap[j]){
			swap(heap[i],heap[j]);
			i=j;
			j=i/2;
		}else break;
	}
}
void createHeap(int n){
	for(int i=n/2;i>=1;i--){
		downAdjust(i,n);
	}
}
void deleteTop(int n){
	heap[1]=heap[n];
	heap.pop_back();
	downAdjust(1,n-1);
}
void insert(int x){
	heap.push_back(x);
	upAdjust(1,heap.size()-1);
}
int main(){
	while(cin>>n){
		heap.clear();
		heap.resize(n+1);
		for(int i=1;i<=n;i++) cin>>heap[i];
		createHeap(heap.size()-1);
		int sum=0;
		while(heap.size()!=2){
			int top=heap[1];
			deleteTop(heap.size()-1);
			top+=heap[1];
			deleteTop(heap.size()-1);
			insert(top);
			sum+=top;
		}
		cout<<sum<<endl;
	}
	return 0;
}

哈夫曼树

计算带权路径长度WPL

//非结构体
struct Cmp{
  bool operator()(const int &a,const int &b)const{
    return a>b;
  }
}
int getWPL(int data[],int n){
  priority_queue<int,vector<int>,Cmp> pq;
  for(int i=0;i<n;i++){
    pq.push(data[i]);
  }
  int sum=0;
  while(pq.size()>1){
    int top=pq.top();
    pq.pop();
    top+=pq.top();
    pq.pop();
    pq.push(top);
    sum+=top;
  }
  return sum;
}

哈夫曼编码

#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
#include<cstring>
using namespace std;
//结构体
struct Node{
  int weight;
  int pos;
  int lchild,rchild;
  Node(){}
  Node(int w,int p,int l,int r):weight(w),pos(p),lchild(l),rchild(r){}
  bool operator < (const Node &tmp)const{
    return weight>tmp.weight;
  }
};
vector<Node> tree;

int index=0;
void HuffmanTree(int data[],int n){
  index=0;
  tree.clear();
  tree.resize(2*n-1);
  priority_queue<Node> pq;  //注意与非结构体区别
  for(int i=0;i<n;i++){
    tree[index].weight=data[i];
    tree[index].pos=index;
    tree[index].lchild=tree[index].rchild=-1;
    pq.push(tree[index++]);
  }
  while(pq.size()>1){
    Node top1=pq.top();
    pq.pop();
    Node top2=pq.top();
    pq.pop();
    tree[index]=Node(top1.weight+top2.weight,index,top1.pos,top2.pos);
    pq.push(tree[index++]);
  }
}
void HuffmanCode(int i,string code){
  if(tree[i].lchild==tree[i].rchild&&tree[i].lchild==-1){  //Huffman树不存在度为1的节点
    cout<<tree[i].weight<<" : "<<code<<endl;
    return;
  }
  //左子树
  code+='0';
  HuffmanCode(tree[i].lchild,code);
  code.erase(code.length()-1,1);
  //右子树
  code+='1';
  HuffmanCode(tree[i].rchild,code);
  code.erase(code.length()-1,1);
}
int main(){
	int n;
	while(cin>>n){
		int* data=new int[n];
		for(int i=0;i<n;i++) cin>>data[i];
		HuffmanTree(data,n);
		string str="";
		HuffmanCode(index-1,str);
	}
	return 0;
}

字符串专题

字符串Hash

只有大写或小写字母

int hashFunc(string str){
  int id=0;
  for(int i=0;i<str.length();i++) id = id * 26 + (str[i] - 'A')
  return id;
}

大小写字母混合

int hashFunc(string str){
  int id=0;
  for(int i=0;i<str.length();i++){
    if('A'<=str[i]<='Z') id=id*52+(str[i]-'A');
    else if('a'<=str[i]<='z') id=id*52+(str[i]-'a')+26;
  }
}

大小写字母以及数字

int hashFunc(string str){
  int id=0;
  for(int i=0;i<str.length();i++){
    if('A'<=str[i]<='Z') id=id*62+(str[i]-'A');
    else if('a'<=str[i]<='z') id=id*62+(str[i]-'a')+26;
    else if('0'<=str[i]<='9') id=id*62+(str[i]-'0')+52;
  }
}

如果数字只出现在末尾

int hashFunc(string str){
  int id=0;
  for(int i=0;i<str.length() - 1;i++) id = id * 26 + (str[i] - 'A')
  id=id*10+(str[str.length()-1]-'0');
  return id;
}

超长字符串Hash（只有小写字母）

#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
const int MOD=1000000007;
const int P = 100000019;
vector<int> ans;
long long hashFunc(string str){
  long long H=0;
  for(int i=0;i<str.length();i++){
    H = (H*P+str[i]-'a') % MOD;
  }
  return H;
}

求解子串Hash值H[i…j]

$$
H[i] = H[i-1] × p + index(str[i])\\
H[i] = index(str[i]) × p^{j-i} + index(str[i+1]) × p^{j-i-1} +…+index(str[j]) × p^{0}
$$
$$
\begin{align}
H[j] & = H[j-1] × p + index(str[j])\\
& = H[j-2] × p^{2} + index(str[j-1]) × p + index(str[j])\\
& = …\\
& = H[i-1] × p^{j-i+1} +H[i…j]\\
\end{align}
$$
$$
So: H[i…j] = H[j] - H[i-1] × p^{j-i+1} \\
= \left(H[j] - H[i-1] × p^{j-i+1}\right)　% mod \\
= \left(\left(H[j] - H[i-1] × p^{j-i+1}\right)　% mod + mod \right) % mod
$$

输入两个长度均不超过1000的字符串，求它们的最长公共子串的长度

#include<iostream>
#include<cstring>
#include<vector>
#include<map>
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long LL;
const LL MOD = 1000000007;
const LL P = 10000019
const LL MAXN=1010;
LL powP[MAXN], H1[MAXN] ={0}, H2[MAXN]={0};
vector<<pair<int,int>> pr1, pr2;
void init(int len){
  powP[0] = 1;
  for(int i=1;i<=len;i++){
    powP[i] = (powP[i-1] * P) % MOD;
  }
}
void calH(LL H[], string &str){
  H[0] = str[0];
  for(int i=1;i<str.length();i++){
    H[i]=(H[i-1] * P + str[i]) %MOD;
  }
}
int calSingleSubH(LL H[], int i, int j){
  if(i==0) reutrn H[j];
  return ((H[j] - H[i-1] * powP[j-i+1]) % MOD + MOD) % MOD;
}
void calSubH(LL H[], int len, vector<pair<int, int>> &pr){
  for(int i=0;i<len;i++){
    for(int j=i;j<len;j++){
      int hashValue=calSingleSubH(H, i, j);
      pr.push_back(make_pair(hashValue, j-i+1));
    }
  }
}
int getMax(){
  int ans=0;
  for(int i=0;i<pr1.size();i++){
    for(int j=0;j<pr2.size();j++){
      if(pr1[i].first==pr2[j].first){
        ans=max(ans, pr1[i].second);
      }
    }
  }
  return ans;
}
int main(){
  string str1, str2;
  getline(cin, str1);
  getline(cin, str2);
  init(max(str1.length(), str2.length()));
  calH(H1, str1);
  calH(H2, str2);
  calSubH(H1, str1.length(), pr1);
  calSubH(H2, str2.length(), pr2);
  printf("ans = %d\n", getMax());
  return 0;
}

KMP算法

KMP算法主要用于解决字符串的匹配问题。即给定两个字符串text与pattern,需要判断pattern是否是text的子串。假设text的长度为n,pattern的长度为m,那么用暴力搜索的算法解决该问题需要的时间复杂度为O(m*n)。这种算法在m,n大于$10^5$级别是无法被接受。而KMP算法需要的时间复杂度仅为$O(m+n)$。

Next数组 $O\left(N\right)$

定义：next[i] 表示使该字符串的子串s[0···i]的前缀s[0···k]和后缀s[i-k···i]相等的最大k(其中k<i，因为前后缀可以重合但不能为整个子串)；如果找不到相等的前后缀组，那么next[i] = -1。
也就是说，next[i]就是所求最长相等前后缀中前缀最后一位的下标！
以字符串s = “ababaab”为例，其对应的next数组为[-1,-1,0,1,2,3,-1]。

• 当i = 0: 子串为”a”，找不到相等的前后缀（因为前后缀不能包含整个s[i])，因此next[0] = -1;
• 当i = 1: 子串为”ab”，找不到相等的前后缀，因此next = -1；
• 当i = 2: 子串为”aba”， k = 0时 “a” = “a”; k = 1时，”ab” != “ba”;因此next[2] = 0;
  依次类推可得到整个next数组。

Next数组计算：
那么如何求解next数组呢？当然暴力的做法是可行的，但不够高效。下面用“递推”的方式来高效求解next数组，即假设已经求出了next[0]…next[i-1]，现在要用它们来退出next[i]。

以“abababc”为例，next数组为[1,-1,0,1,2,3,-1]。
假设已经有了next[0…3]，求next[4]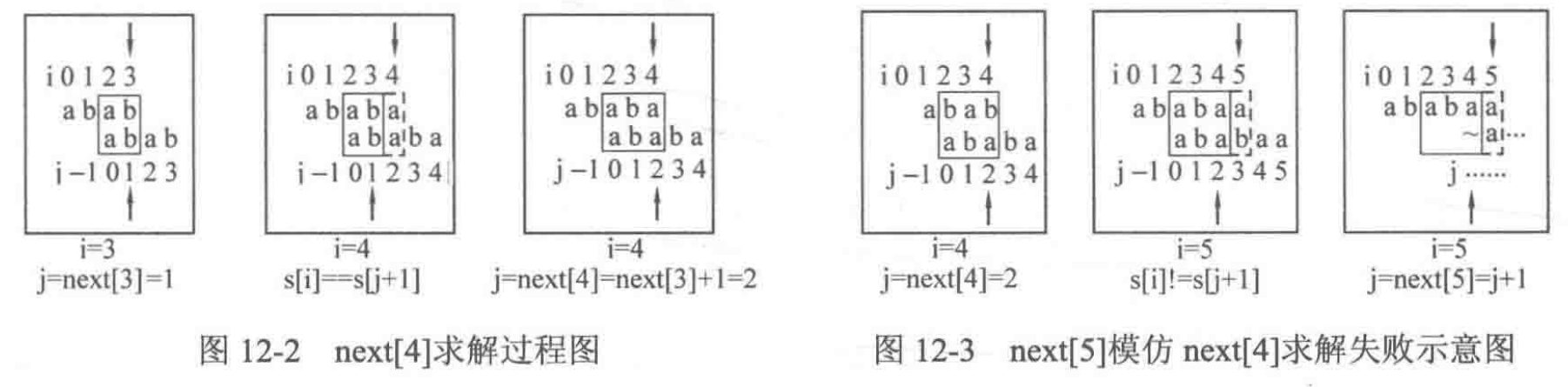

• ①如果s[i]==s[j+1],则next[i]=j+1;
• ②否则，j=next[j],回到①，一直到①满足或者j==-1时停止。
  ①②的前提是前后缀s[i-j…i]与s[0…j]相等，
• ①的思想好理解，如果s[i]==s[j+1]，，那么增加；
• ②的思想是，s[i]!=s[j+1]，那么回退j，但是希望j尽可能大，那么当然希望取s[i-j…i]这一段的最长前后缀了！然后比较s[i]与s[j+1]，如果还不相等继续回退，直到j==-1或者s[i]==s[j+1]为止。所以从这个角度将，next数组的意义就是当j+1适配是，j应当回退的位置！

  int* getNext(string str){
    int len=str.length();
    int* next=new int[len];
    next[0]=-1;
    int j=next[0];
    for(int i=1;i<len;i++){
      while(j!=-1&&str[i]!=str[j+1]){//回退
        j=next[j];
      }
      if(str[i]==str[j+1]){
        j++;
      }
      next[i]=j;
    }
    return next;
  }

  时间复杂度分析：
  首先i肯定是$O(n)$的，那么j呢?注意到j只在一个地方增加，最多增加n次，而j在while中的减小最多只能减少n次。因此整个过程中j最多执行n次，那么j也是$O(n)$的，所以整体复杂度$O(n)$

  KMP算法 $O\left(N+M\right)$

  KMP算法与next数组的过程十分相似，具体过程如下
• ①初始化j=-1，表示pattern当前已被匹配的最后位；
• ②让i遍历文本串text，对每个i，执行③④来试图匹配text[i]和pattern[j+1]；
• ③不断令j=next[j]，直到j回退为-1，或是text[i]==pattern[j+1]成立；
• ④如果text[i]==pattern[j+1]，则令j++。如果j达到了m-1，说明pattern是text的子串。

  bool KMP(string text, string pattern){
    int n=text.length(), m =pattern.length();
    int* next=getNext(pattern);
    int j=-1;
    for(int i=0;i<n;i++){
      while(j!=-1&&text[i]!=pattern[j+1]){
        j=next[j];
      }
      if(text[i]==pattern[j+1]){
        j++;
      }
      if(j==m-1){
        return true;
      }
    }
    return false;
  }

  匹配次数

  int KMP(string text, string pattern){
  	int n = text.length(), m =pattern.length();
  	int j = -1;
  	int ans = 0;
  	int* next = getNext(pattern);
  	for(int i=0;i<n;i++){
  		while(j!=-1&&text[i]!=pattern[j+1]){
  			j=next[j];
  		}
  		if(text[i]==pattern[j+1]){
  			j++;
  		}
  		if(j==m-1){ //相等时回退
  			ans++;
  			j=next[j];
  		}
  	}
  	return ans;
  }

  Nextval数组

  进一步优化next数组，因为当s[j+1]!=s[i]时，如果j=next[j]回退操作还是使得s[i]==s[j+1]，那么没有意义，一个想法是继续回退，但还是存在若干无意义的回退，这里需要修改next数组的含义进行一次回退，即nextval[i]表示当模式串pattern的i+1为失配时，i应当回退到的最佳位置。
• 在next记得的next[i]的位置j的基础上，进行优化
• 如果j==-1（不需要回退）或者pattern[i+1]!=patternj+1

  int* getNextval(string str){
    int len=str.length();
    int* nextval=new int[len];
    nextval[0]=-1;
    int j=nextval[0];
    for(int i=1;i<len;i++){
      while(j!=-1&&str[i]!=str[j+1]){
        j=next[j];
      }
      if(str[i]==str[j+1]){
        j++;
      }
      //不用判断i+1是否超过了len-1，因为从nextval的含义上讲，如果i已经是模式串pattern的最后一位，那么i+1位失配的说法没有意义
      //其次s[len]=='\0'，且j一定小于i，因此一定会失配。
      if(j==-1||str[i+1]!=str[j+1]){ //此时回退是无意义的
        nextval[i]=j;
      }else nextval[i]=nextval[j]; //此时需要再次回退，因为str[i+1]==str[j+1]，即下一次匹配i与j+1时失配了，回退！因为希望下一次得到的就是最佳位置。
    }
    return nextval;
  }

  问题 A: 动物简介(animal)

题目描述
到了动物园，琦琦开心得跳起来。哗，这里好多动物呀，有老虎，有狮子……，在开心之余，琦琦也不忘妈妈的教导：观察动物时要认真仔细，还要看动物园附上的动物简介呀。动物的简介原来还有英文版的呢！为了卖弄自己的英文水平，琦琦就告诉妈妈每张动物简介里出现了多少次该动物的名称。注意：琦琦只认识小写字母，而且她只认得动物的单词，因此她认为monkeys或者smonkey或者smonkeys都是出现了monkey这个词。
你能编程完成琦琦的任务吗？
输入
输入文件共n+2行：
第1行为数字n（n<=3000），表示该动物的简介共有n行。
第2行为一个单词，表示琦琦认识的动物名称。
接着是n行，每行为一个长度小于250个字符的字符串，表示动物的简介。
输出
　输出文件共1行，为简介里出现了多少次琦琦能识别出的动物的单词。
样例输入
2
snake
The snake is a long and thin animal.
Snakes have no legs or feet.
样例输出
1

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN=251;
int n;
string pattern, text;
int* getNextval(string str){
	int len=str.length();
	int* nextval=new int[len];
	nextval[0]=-1;
	int j=nextval[0];
	for(int i=1;i<len;i++){
		while(j!=-1&&str[i]!=str[j+1]){
			j=nextval[j];
		}
		if(str[i]==str[j+1]) j++;
		if(j==-1||str[i+1]!=str[j+1]) nextval[i]=j;
		else nextval[i]=nextval[j];
	}
	return nextval;
}
int KMP(string text, string pattern){
	int n=text.length(), m=pattern.length();
	int* nextval=getNextval(pattern);
	int j=-1;
	int ans=0;
	for(int i=0;i<n;i++){
		while(j!=-1&&text[i]!=pattern[j+1]){
			j=nextval[j];
		}
		if(text[i]==pattern[j+1]) j++;
		if(j==m-1){
			ans++;
			j=nextval[j];
		}
	}
	delete [] nextval;
	return ans;
}
int main(){
	cin>>n;
	getchar();
	getline(cin,pattern);
	int ans=0;
	for(int i=0;i<n;i++){
		getline(cin,text);
		ans+=KMP(text,pattern);
	}
	cout<<ans<<endl;
	return 0;
}

问题 B: P2 统计单词数

题目描述
统计单词数 (stat.cpp/c/pas)
一般的文本编辑器都有查找单词的功能，该功能可以快速定位特定单词在文章中的位置，有的还能统计出特定单词在文章中的次数。
现在，请你编程实现这一功能，具体要求是：给定一个单词，请你输出它在给定的文章中出现的次数和第一次出现的位置。注意：匹配单词时，不区分大小写，但要求完全匹配，即单词必须与文章中某一独立残次在不区分大小写的情况下完全相同（参见样例1），如果给定单词仅是文章中某一单词的一部分则不算匹配（参见样例2）。
输入
输入文件共2行。
第1行为一个字符串，其中只包含字母，表示给定单词；
第2行为一个字符串，其中只可能包含字母和空格，表示给定的文章。
输出
只有1行，如果在文章中找到给定单词则输出两个整数，两个整数之间用一个空格隔开，分别是单词在文章中出现的次数和第一次出现的位置（即在文章中第一次出现时，单词首字母在文章中的位置，位置从0开始）；如果单词在文章中没有出现，则直接输出一个整数-1。
样例输入
输入样例1：
To
to be or not to be is a question
输入样例2：
to
Did the Ottoman Empire lose its power at that time
样例输出
输出样例1：
2 0
输出样例2：
-1

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
string pattern, text;
int* getNextval(string str){
	int len=str.length();
	int* nextval=new int[len];
	nextval[0]=-1;
	int j=nextval[0];
	for(int i=1;i<len;i++){
		while(j!=-1&&str[i]!=str[j+1]){
			j=nextval[j];
		}
		if(str[i]==str[j+1]){
			j++;
		}
		if(j==-1||str[i+1]!=str[j+1]) nextval[i]=j;
		else nextval[i]=nextval[j];
	}
	return nextval;
}
int KMP(string text, string pattern, int &idx){
	int n=text.length(), m=pattern.length();
	int* nextval=getNextval(pattern);
	bool bFirst=true;
	int j=-1;
	int ans=0;
	for(int i=0;i<n;i++){
		while(j!=-1&&text[i]!=pattern[j+1]){
			j=nextval[j];
		}
		if(text[i]==pattern[j+1]) j++;
		if(j==m-1){
			if(((i<n-1&&text[i+1]==' ')||i==n-1)
				&&((i-m>0&&text[i-m]==' ')||i-m+1==0)){
				ans++;
				if(bFirst){
					bFirst=false;
					idx=i-m+1;
				}
			}
			j=nextval[j];
		}
	}
	return ans;
}
void convert(string &str){
	for(int i=0;i<str.length();i++){
		if('a'<=str[i]&&str[i]<='z') str[i]-='a'-'A';
	}

}
int main(){
	getline(cin, pattern);
	getline(cin, text);
	convert(pattern);
	convert(text);
	int idx=0;
	int ans=KMP(text, pattern, idx);
	if(ans!=0) cout<<ans<<" "<<idx<<endl;
	else cout<<-1<<endl;
	return 0;
}

问题 C: 剪花布条

题目描述
一块花布条，里面有些图案，另有一块直接可用的小饰条，里面也有一些图案。对于给定的花布条和小饰条，计算一下能从花布条中尽可能剪出几块小饰条来呢？
输入
输入中含有一些数据，分别是成对出现的花布条和小饰条，其布条都是用可见ASCII字符表示的，可见的ASCII字符有多少个，布条的花纹也有多少种花样。花纹条和小饰条不会超过1000个字符长。如果遇见#字符，则不再进行工作。
输出
输出能从花纹布中剪出的最多小饰条个数，如果一块都没有，那就老老实实输出0，每个结果之间应换行。
样例输入

abcde a3
aaaaaa  aa
#

样例输出
0
3

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
string text, pattern;
int* getNextval(string str){
	int len=str.length();
	int* nextval=new int[len];
	nextval[0]=-1;
	int j=nextval[0];
	for(int i=1;i<len;i++){
		while(j!=-1&&str[i]!=str[j+1]){
			j=nextval[j];
		}
		if(str[i]==str[j+1]) j++;
		if(j==-1||str[i+1]!=str[j+1]) nextval[i]=j;
		else nextval[i]=nextval[j];
	}
	return nextval;
}
int KMP(string text, string pattern){
	int n=text.length(), m=pattern.length();
	int* nextval=getNextval(pattern);
	int j=-1;
	int ans=0;
	for(int i=0;i<n;i++){
		while(j!=-1&&text[i]!=pattern[j+1]){
			j=nextval[j];
		}
		if(text[i]==pattern[j+1]){
			j++;
		}
		if(j==m-1){
			ans++;
			j=-1;
		}
	}
	return ans;
}
int main(){
	while(cin>>text&&text!="#"){
		cin>>pattern;
		int ans=KMP(text, pattern);
		cout<<ans<<endl;
	}

	return 0;
}

最长回文串

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：
输入: “babad”
输出: “bab”
注意: “aba” 也是一个有效答案。

示例 2：
输入: “cbbd”
输出: “bb”

动态规划

设DP[i][j]为[i,j]是否为回文串，是为1，否为0；
状态转移方程：DP[i][j]=DP[i+1][j-1]&(s[i]==s[j])
时间复杂度：$O(n^2)$

class Solution {
public:
    string longestPalindrome(string s) {
        int n=s.length();
        if(n==0) return s;
        vector<vector<int>> DP;
        DP.resize(n);
        int maxLen=1, l=0, r=0;
        for(int i=0;i<n;i++){
            DP[i].resize(n, 0);
            DP[i][i]=1;
        }
        for(int i=0;i<n-1;i++){
            if(s[i]==s[i+1]){
                DP[i][i+1]=1;
                if(maxLen==1){
                    maxLen=2;
                    l=i;
                    r=i+1;
                }
            }
        }
        for(int len=3;len<=n;len++){
            for(int i=0;i+len-1<n;i++){
                int j=i+len-1;
                if(s[i]==s[j]) DP[i][j]=DP[i+1][j-1];
                if(DP[i][j]==1&&len>maxLen){
                    maxLen=len;
                    l=i;
                    r=j;
                }
            }
        }
        // cout<<l<<" "<<maxLen<<endl;
        return s.substr(l, maxLen);
    }
};

中心扩展法

由于存在奇数的回文串和偶数的回文串，所以需要从一个字符开始扩展或者从两个字符之间进行扩展。
时间复杂度：$O(n^2)$

class Solution {
public:
    string longestPalindrome(string s) {
        int n=s.length();
        int start, end;
        start=end=0;
        for(int i=0;i<n;i++){
            pair<int,int> p1=expandAroundCenter(s, i, i);
            pair<int,int> p2=expandAroundCenter(s, i, i+1);
            pair<int,int> p;
            if(p1.second-p1.first>=p2.second-p2.first) p=p1;
            else p=p2;
            if(p.second-p.first>end-start){
                start=p.first;
                end=p.second;
            }
        }
        return s.substr(start, end-start+1);
    }
    pair<int,int> expandAroundCenter(string& s, int left, int right){
        int n=s.length();
        while(left>=0&&right<n&&s[left]==s[right]){
            left--;
            right++;
        }
        return {++left, --right};
    }
};

马拉车算法（Manacher’s Algorithm）

（1）首先对原始字符串用其不包含的字符进行扩充，例如用’#’，得到的字符串长度一定为奇数
（2）其次设P[i]为处理后的串的每个字符对应的以i为中心的回文串长度，其在原始字符串的起始坐标为(i-P[i])/2
（3）利用对称性，更新P[i]、R、C。详见参考：
参考链接
时间复杂度：$O(n)$

class Solution {
public:
    string longestPalindrome(string s) {
        int n=s.length();
        if(n<2) return s;
        string str=addBoundaries(s, '#');
        n=str.length();
        int P[n];
        memset(P, 0, sizeof(P));
        int R=0,C=0; //右边界与中心点,R=C+P[C],P[i]表示以i为中心点的原始回文串长度，也可以表示处理后的字符串的以i为中心的回文串半径，处理后的字符串长度一定为奇数
        int start=0, end=0; //最长回文串的起始位置

        for(int i=0;i<n;i++){
            if(i<R){
                int i_mirror = 2 * C - i;//i关于center对承德店i_mirror
                //P[i_mirror]的三种情况
                //①P[i_mirror]<R-i,P[i]=P[i_mirror],无需扩展
                //②P[i_mirror]=R-i,P[i]=P[i_mirror]，需要扩展
                //③P[i_mirror]>R-i，P[i]=R-i，无需扩展
                //min精髓，当然后面还要考虑是否中心扩展
                P[i]=min(R-i, P[i_mirror]);
            }

            int left=i-P[i]-1;
            int right=i+P[i]+1;
            while(left>=0&&right<n&&str[left]==str[right]){
                P[i]++;
                left--;
                right++;
            }
            if(i+P[i]>R){ //更新R,C
                R=i+P[i];
                C=i;
            }
            if(P[i]>end-start+1){
                start=(i-P[i])/2; //起始点关系
                end=start+P[i]-1;
            }
        }
        return s.substr(start, end-start+1);
    }


    string addBoundaries(string s, char divide){ //分隔符divide必须是字符串中未出现的字符
        int n=s.length();
        if(n==0) return "";
        string res;
        for(int i=0;i<n;i++){
            res+=divide;
            res+=s[i];
        }
        res+=divide;
        return res;
    }
};

专题扩展

分块思想

假设一个非负整数序列$A$，元素个数为$N$（$N\leq 10^{5},A[i]\leq 10^{5}$），随时可能添加和删除元素的情况下，实时查询元素第K大的元素
思路：
将序列分为$\lceil\sqrt{N}\rceil$块，每块$\lfloor\sqrt{N}\rfloor$个元素，设置一个hash数组table[100001]，其中table[x]表示整数x的当前存在个数
设置一个统计数组block[317]，其中block[i]表示第i块中存在的元素的个数：
block[0]:0…315
block[1]:316…631
…
block[316]:99856…100000
新增元素：table[x]++, block[x/316]++
删除元素：table[x]–, block[x/316]]–
查找第N大元素，先确定块号，以及能否达到个数N，如果能，块号i，则从i*316开始在table开始从小达到找
时间复杂度$O\left(\sqrt{N}\right)$

A1057 Stack(30)

Description
Stack is one of the most fundamental data structures, which is based on the principle of Last In First Out (LIFO). The basic operations include Push (inserting an element onto the top position) and Pop (deleting the top element). Now you are supposed to implement a stack with an extra operation: PeekMedian – return the median value of all the elements in the stack. With N elements, the median value is defined to be the (N/2)-th smallest element if N is even, or ((N+1)/2)-th if N is odd.
Input Specification
Each input file contains one test case. For each case, the first line contains a positive integer N ($≤10^{5}$). Then N lines follow, each contains a command in one of the following 3 formats:
Push key
Pop
PeekMedian
where key is a positive integer no more than $10^{5}$.
Output Specification
For each Push command, insert key into the stack and output nothing. For each Pop or PeekMedian command, print in a line the corresponding returned value. If the command is invalid, print Invalid instead.
Sample Input
17
Pop
PeekMedian
Push 3
PeekMedian
Push 2
PeekMedian
Push 1
PeekMedian
Pop
Pop
Push 5
Push 4
PeekMedian
Pop
Pop
Pop
Pop
Sample Output
Invalid
Invalid
3
2
2
1
2
4
4
5
3
Invalid
Procedure

#include<iostream>
#include<algorithm>
#include<cstring>
#include<stack>
using namespace std;
const int MAXN=100010;
const int SQRN=316;
stack<int> st;
int block[SQRN];
int table[MAXN];
void peekMedian(int K){
	int sum=0;
	int idx=0;
	while(sum+block[idx]<K){
		sum+=block[idx++];
	}
	int num=idx*SQRN;
	while(sum+table[num]<K){
		sum+=table[num++];
	}
	cout<<num<<endl;
}
void Push(int x){
	st.push(x);
	block[x / SQRN] ++;
	table[x]++;
}
void Pop(){
	int x=st.top();
	st.pop();
	block[x /SQRN]--;
	table[x]--;
	cout<<x<<endl;
}
int main(){
	int x, query;
	memset(block, 0, sizeof(block));
	memset(table, 0, sizeof(table));
	string str;
	cin>>query;
	for(int i=0;i<query;i++){
		cin>>str;
		if(str=="Push"){
			cin>>x;
			Push(x);
		}else if(str=="Pop"){
			if(st.empty()){
				cout<<"Invalid"<<endl;
			}else Pop();
		}else if(str=="PeekMedian"){
			if(st.empty()) cout<<"Invalid"<<endl;
			else{
				int K=st.size();
				if(K%2==0) K/=2;
				else K=(K+1)/2;
				peekMedian(K);
			}
		}
	}
}

树状数组

由于计算机中存储整数一般采用补码，所以一个补码表示的整数x的相反数-x相当于把x的二进制的每一位都取反，然后末位加1。lowbit(x)=x&(-x)可以理解为取x的二进制最右边的1和它右边所有0，因此其一定是2的幂次，及1、2、4、8等，其也可理解为能整除x的最大2的幂次。树状数组C，其中C[i]存放数组A中i号位之前lowbit(i)个元素之和，显然C[i]的覆盖长度是lowbit(i)，注意C[i]下标从1开始

i	1	2	3	4	…	n
lowbit(i)	1	2	1	4	…	n&(-n)

即C[1]=A[1]
C[2]=A[1]+A[2]
C[3]=A[3]
C[4]=A[1]+A[2]+A[3]+A[4]
C[5]=A[5]
C[6]=A[5]+A[6]
C[7]=A[7]
①设计函数getSum(x)，返回前x个数之和A[1]+…A[x]
记：$Sum(1,x)=A[1]+…A[x]$
而$C[x]=A[x-lowbit(x)+1]+…+A[x]$
所以$Sum(1,x)=A[1]+…+A[x-lowbit(x)]+A[x-lowbit(x)+1]+…+A[x]$
$=Sum(1,x-lowbit(x))+C[x]$

int getSum(int x){
  int sum=0;
  for(int i=x;i>0;i-=lowbit(i)){
    sum+=C[i];
  }
  return sum;
}

时间复杂度：$O\left(\log{N}\right)$
②设计函数update(x,v)，实现将第x个数加上一个数v的功能，即A[x]+=v
如何找到离$C[x]$最近的能覆盖$C[x]$的$C[y]$呢？
首先：$lowbit(y)$必须大于$lowbit(x)$，所以问题等价求一个尽可能校的整数a，使得$lowbit(x+a)>lowbit(x)$，
而$lowbit(x)$是取二进制最右边的1的位置，因此如果$lowbit(a)<lowbit(x)$，$lowbit(x+a)$就会小于$lowbit(x)$，因此$lowbit(a)$必须不小于$lowbit(x)$。
所以当$a$取$lowbit(x)$时，二进制进位得到$lowbit(x+a)>lowbit(x)$，所以最小的a就是$lowbit(x)$。

void update(int x,int v){
  for(int i=x;i<=N;i+=lowbit(i)){
    C[i]+=v;
  }
}

时间复杂度：$O\left(\log{N}\right)$

经典应用①

给定一个有N个正整数的序列$A(N\leq 10^{5}, A[i]\leq 10^{5})$，对序列中的每个数，求出序列中它左边比它小的数的个数。
做法一：Hash数组，记录Hash[A[i]]++,最后统计sum=Hash[A[i]]+…+Hash[A[i]-1]，时间复杂度：$O\left(N^{2}\right)$
做法二：树状数组，时间复杂度：$O\left(N\log{N}\right)$

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int MAXN=100010;
#define lowbit(i) ((i)&(-i))
int C[MAXN];
void update(int x, int v){
  for(int i=x;i<=MAXN;i+=lowbit(i)){
    C[i]+=v;
  }
}
int getSum(int x){
  int sum=0;
  for(int i=x;i>0;i-=lowbit(i)){
    sum+=C[x];
  }
  return sum;
}
int main(){
  int n,x;
  cin>>n;
  memset(C, 0, sizeof(C));
  for(int i=0;i<n;i++){
    cin>>x;
    update(x, 1);
    cout<<getSum(x-1)<<endl;
  }
  return 0;
}

如何统计元素左边比该元素大的个数，等价于求Hash[A[i]+1]+…+Hash[A[N]]，所以getSum(N)-getSum(A[i])就是答案。
如何统计元素右边比该元素小（或大）的个数，只需要把原始数组从右往左遍历就好了。

经典应用②

$A[i]\leq N$不成立，离散化(只适用离线查询，因为需要全部数据确定后才能进行离散化)：
{99999999,18,666,88888}对应{4,1,2,3}

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstring>
using namespace std;
const int MAXN=100010;
#define lowbit(i) ((i)&(-i))
struct Node{
  int val;
  int pos;
}temp[MAXN];
int A[MAXN];
int C[MAXN];
void update(int x, int v){
  for(int i=x;i<MAXN;i+=lowbit(i)){
    C[i]+=v;
  }
}
int getSum(int x){
  int sum=0;
  for(int i=x;i>0;i-=lowbit(i)){
    sum+=C[x];
  }
  return sum;
}
bool cmp(Node a, Node b){
  return a.val<b.val;
}
int main(){
  int n;
  cin>>n;
  memset(C, 0, sizeof(C));
  for(int i=0;i<n;i++){
    cin>>temp[i].val;
    temp[i].pos=i;
  }
  //离散化
  sort(temp, temp+n, cmp);
  for(int i=0;i<n;i++){
    if(i==0||temp[i].val!=temp[i-1].val){
      A[temp[i].pos]=i+1;
    }else{
      A[temp[i].pos]=A[temp[i-1].pos];
    }
  }
  for(int i=0;i<n;i++){
    update(A[i], 1);
    cout<<getSum(A[i]-1)<<endl;
  }
  return 0;
}

经典应用③

求序列第K大的数。
树状数组二分法：
l=1, r=MAXN，求满足$hash[1]+…+hash[i]\geq K$成立的最小i。

int findKthElement(int K){
  int l=1, r=MAN, mid;
  while(l<r){
    mid=(l+r)/2;
    if(getSum(mid)>=K) r=mid;
    else l=mid+1;
  }
  return l;
}

时间复杂度：$O\left(\log^2{n}\right)$

二维树状数组

给定一个二维整数矩阵A，求A[1][1]~A[x][y]这个子矩阵中所有元素之和，以及给单点A[x][y]加上整数v。

int C[MAXN][MAXN];
void update(int x, int y, int v){
  for(int i=x;i<=MAXN;i+=lowbit(i)){
    for(int j=y;j<=MAXN;j+=lowbit(j)){
      C[i][j]+=v;
    }
  }
}
int getSum(int x, int y){
  int sum=0;
  for(int i=x;i>0;i-=lowbit(i)){
    for(int j=y;y>0;j-=lowbit(j)){
      sum+=C[i][j];
    }
  }
  return sum;
}

区间更新，单点查询

之前都是对树状数组进行单点更新，区间查询，这里进行区间更新，单点查询
①设计getSum(x)，返回A[x]
C[i]不再表示这段区间的元素之和，而是表示这段区间每个数当前被加了多少。
例如A[5]=C[5]+C[6]+C[8]+[16]
A[i]的值实际上就是覆盖它的若干个“矩形”C[i]的值之和。

int getSum(int x){
  int sum=0;
  for(int i=x;i<MAXN;i+=lowbit(i)){
    sum+=C[i];
  }
  return sum;
}

②设计update(x, v)，将A[1]…A[x]的每个数都加上一个数v

void update(int x, int v){
  for(int i=x;i>0;i-=lowbit(i)){
    C[i]+=v;
  }
}

区间查询

题目描述
食堂有N个打饭窗口，现在正到了午饭时间，每个窗口都排了很多的学生，而且每个窗口排队的人数在不断的变化。
现在问你第i个窗口到第j个窗口一共有多少人在排队？
输入
输入的第一行是一个整数T，表示有T组测试数据。
每组输入的第一行是一个正整数N（N<=30000），表示食堂有N个窗口。
接下来一行输入N个正整数，第i个正整数ai表示第i个窗口最开始有ai个人排队。（1<=ai<=50）
接下来每行有一条命令，命令有四种形式：
(1)Add i j，i和j为正整数，表示第i个窗口增加j个人（j不超过30）；
(2)Sub i j，i和j为正整数，表示第i个窗口减少j个人（j不超过30）；
(3)Query i j，i和j为正整数，i<=j，表示询问第i到第j个窗口的总人数；
(4)End 表示结束，这条命令在每组数据最后出现；
每组数据最多有40000条命令。
输出
对于每组输入，首先输出样例号，占一行。
然后对于每个Query询问，输出一个整数，占一行，表示询问的段中的总人数，这个数保持在int以内。
样例输入
1
10
1 2 3 4 5 6 7 8 9 10
Query 1 3
Add 3 6
Query 2 7
Sub 10 2
Add 6 3
Query 3 10
End
样例输出
Case 1:
6
33
59

#include<iostream>
#include<algorithm>
#include<cstring>
#define lowbit(i) ((i)&(-i))
using namespace std;
const int MAXN=30001;
int C[MAXN];
int T, N, x;
int getSum(int x){
	int sum=0;
	for(int i=x;i>0;i-=lowbit(i)) sum+=C[i];
	return sum;
}
void update(int x, int v){
	for(int i=x;i<MAXN;i+=lowbit(i)){
		C[i]+=v;
	}
}
int main(){
	cin>>T;
	for(int i=1;i<=T;i++){
		memset(C,0,sizeof(C));
		cin>>N;
		for(int j=0;j<N;j++){
			cin>>x;
			update(j+1, x);
		}
		string str;
		int a, b;
		bool bFirst=true;
		while(cin>>str&&str!="End"){
			cin>>a>>b;
			if(str=="Query"){
				if(bFirst){
					bFirst=false;
					cout<<"Case "<<i<<":"<<endl;
				}
				cout<<getSum(b)-getSum(a-1)<<endl;
			}else if(str=="Add"){
				update(a, b);
			}else if(str=="Sub"){
				update(a, -b);
			}
		}
	}

	return 0;
}

最少的交换

题目描述
现在给你一个由n个互不相同的整数组成的序列，现在要求你任意交换相邻的两个数字，使序列成为升序序列，请问最少的交换次数是多少？
输入
输入包含多组测试数据。每组输入第一行是一个正整数n（n<500000），表示序列的长度，当n=0时。
接下来的n行，每行一个整数a[i]（0<=a[i]<=999999999），表示序列中第i个元素。
输出
对于每组输入，输出使得所给序列升序的最少交换次数。
样例输入
5
9
1
0
5
4
3
1
2
3
0
样例输出
6
0

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#define lowbit(i) ((i)&(-i))
using namespace std;
const int MAXN=500010;
int C[MAXN];
int A[MAXN];
struct Node{
	int val;
	int pos;
};
Node node[MAXN];
void update(int x, int v){
	for(int i=x;i<MAXN;i+=lowbit(i)) C[i]+=v;
}
int getSum(int x){
	int sum=0;
	for(int i=x;i>0;i-=lowbit(i)) sum+=C[i];
	return sum;
}
bool cmp(Node a, Node b){
	return a.val<b.val;
}
int main(){
	int n;
	while(cin>>n&&n!=0){
		memset(C,0,sizeof(C));
		memset(A,0,sizeof(A));
		int sum=0;
		for(int i=0;i<n;i++){
			cin>>node[i].val;
			node[i].pos=i;
		}
		//离散化
		sort(node, node+n,cmp);
		for(int i=0;i<n;i++){
			if(i==0||node[i-1].val!=node[i].val){
				A[node[i].pos]=i+1;
			}else A[node[i].pos]=A[node[i-1].pos];
		}
		for(int i=0;i<n;i++){
			update(A[i],1);
			sum+=getSum(n)-getSum(A[i]);
		}
		cout<<sum<<endl;
	}
	return 0;
}

字典树

原理

作用

1、维护字符串集合（即字典）。
2、向字符串集合中插入字符串（即建树）。
3、查询字符串集合中是否有某个字符串（即查询）。
4、统计字符串在集合中出现的个数（即统计）。
5、将字符串集合按字典序排序（即字典序排序）。
6、求集合内两个字符串的LCP（Longest Common Prefix，最长公共前缀）（即求最长公共前缀）, 逆序字符串即可求后缀。

代码

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
#include<functional>
using namespace std;
struct Node{
	int numbers;	//当前字符为字符串结尾的次数
	bool wordEnd;  //是否为字符串结尾
	Node* next[26];
	Node(){}
};
Node* newNode(){
	Node* node = new Node();
	node->numbers=0;
	node->wordEnd=false;
	for(int i=0;i<26;i++) node->next[i]=NULL;
  return node;
}
void create(Node* root, string str){
	Node* node = root;
	int idx=0;
	int len=str.length();
	while(idx<len){
		if(node->next[str[idx]-'a']==NULL){
			Node* tmp=newNode();
			node->next[str[idx]-'a']=tmp;
		}
		node=node->next[str[idx]-'a'];
		if(idx==len-1){
			node->numbers++;
			node->wordEnd=true;
		}	 
		idx++;
	}
}
int search(Node* root, string str){
	int idx=0;
	int len=str.length();
	while(idx<len){
		if(root->next[str[idx]-'a']==NULL) return 0;
		root=root->next[str[idx]-'a'];
		idx++;
	}
	return root->numbers;
}
void deleteNode(Node* root){
	for(int i=0;i<26;i++){
		if(root->next[i]!=NULL){
      deleteNode(root->next[i]);
    }
	}
	delete root;
}
int main(){
//	int a=1;
//	int b=1;
//	function<void(int, int)> fun = [=,&a](int a, int b)->void{a=2;b=2;};
//	fun(a, b);
//	cout<<a<<b<<endl;
	string s1="abc";
	string s2="ab";
	string s3="abcd";
	Node* root=newNode();
	create(root, s1);;
	create(root, s2);
	create(root, s2);
	create(root, s3);
	cout<<search(root,s1)<<endl;
	cout<<search(root,s2)<<endl;
	cout<<search(root,s3)<<endl;
	cout<<search(root,"cd")<<endl;
	return 0;
}

单调栈

概念

单调栈实际上就是栈，只是利用一些巧妙的逻辑，使得每次新元素入栈后，栈内的元素都保持有序（单调递增或单调递减）。

听起来有点像堆，其实不然，单调栈用途不太广泛，只处理一种典型的问题，叫做Next Greater Element。

Next Greater Element

一个数组，找出每个元素右边比其大的第一个元素。
这个问题可以抽象为：把数组每个元素想象成并列站立的人，元素值想象成身高，这些人站一列，求右边第一个挡住自己视线的人即可。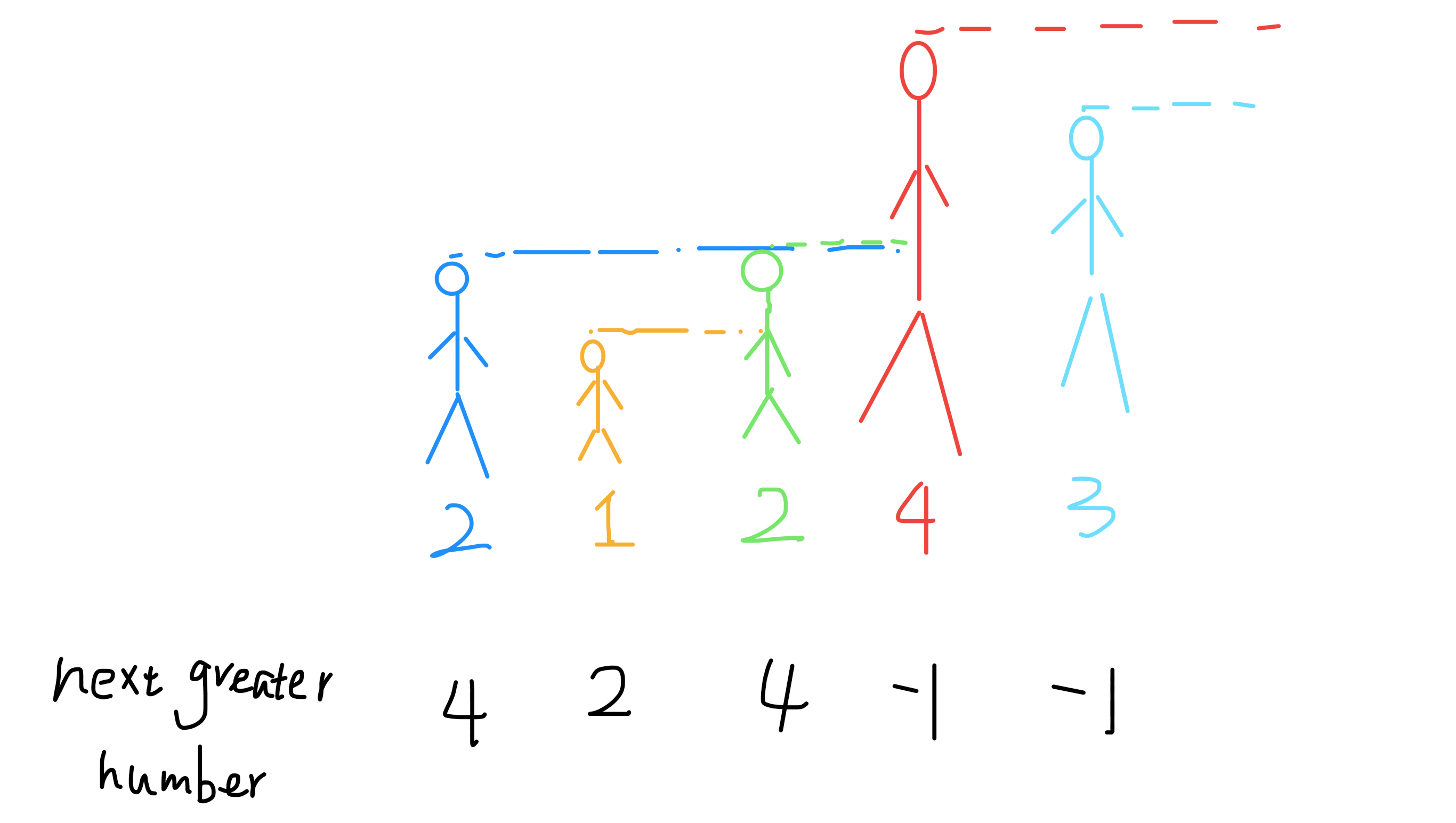

vector<int> nextGreaterElement(vector<int>& nums){
  vector<int> res(nums.size());
  stack<int> st;
  for(int i=nums.size()-1;i>=0;i--){
    while(!st.empty()&&st.top()<nums[i]) st.pop();//所有右边比当前元素小的都出栈，因为它们肯定不是
    res[i]=st.empty()?-1:st.top();
    st.push(nums[i]); //入栈
  }
  return res;
}

时间复杂度：$O(n)$ —— 总体上看，总共n个元素，每个元素最多入栈和出栈一次，所以while的总体复杂度为$O(n)$，所以整个for循环以及while总体都是$O(n)$

每日温度

给你一个数组 T = [73, 74, 75, 71, 69, 72, 76, 73]，这个数组存放的是近几天的天气气温（这气温是铁板烧？不是的，这里用的华氏度）。你返回一个数组，计算：对于每一天，你还要至少等多少天才能等到一个更暖和的气温；如果等不到那一天，填 0 。

举例：给你 T = [73, 74, 75, 71, 69, 72, 76, 73]，你返回 [1, 1, 4, 2, 1, 1, 0, 0]。
解释：第一天 73 华氏度，第二天 74 华氏度，比 73 大，所以对于第一天，只要等一天就能等到一个更暖和的气温。后面的同理。

你已经对 Next Greater Number 类型问题有些敏感了，这个问题本质上也是找 Next Greater Number，只不过现在不是问你 Next Greater Number 是多少，而是问你当前距离 Next Greater Number 的距离而已。

相同类型的问题，相同的思路，直接调用单调栈的算法模板，稍作改动就可以啦，直接上代码把。

vector<int> dailyTemperatures(vector<int>& T){
  vector<int> res(T.size());
  stack<int> st;
  for(int i=T.size()-1;i>=0;i--){
    while(!st.empty()&&T[st.top()]<T[i]) st.pop();
    res[i]=st.empty()?0:st.top()-i;
    st.push(i);
  }
  return res;
}

欧拉图

「一笔画」问题与欧拉图或者半欧拉图有着紧密的联系，下面给出定义：

• 通过图中所有边恰好一次且行遍所有顶点的通路称为欧拉通路。
• 通过图中所有边恰好一次且行遍所有顶点的回路称为欧拉回路。
• 具有欧拉回路的无向图称为欧拉图。
• 具有欧拉通路但不具有欧拉回路的无向图称为半欧拉图。
  如果没有保证至少存在一种合理的路径，我们需要判别这张图是否是欧拉图或者半欧拉图，具体地：
• 对于无向图 G，G 是欧拉图当且仅当 G 是连通的且没有奇度顶点。
• 对于无向图 G，G 是半欧拉图当且仅当 G 是连通的且 G 中恰有 2 个奇度顶点。
• 对于有向图 G，G 是欧拉图当且仅当 G 的所有顶点属于同一个强连通分量且每个顶点的入度和出度相同。
• 对于有向图 G，G 是半欧拉图当且仅当 G 的所有顶点属于同一个强连通分量且
• 恰有一个顶点的出度与入度差为 1；
• 恰有一个顶点的入度与出度差为 1；
• 所有其他顶点的入度和出度相同。
  注意对于每一个节点，它只有最多一个「死胡同」分支。依据前言中对于半欧拉图的描述，只有那个入度与出度差为 1 的节点会导致死胡同。

LeetCode 332. 重新安排行程

Description
给定一个机票的字符串二维数组 [from, to]，子数组中的两个成员分别表示飞机出发和降落的机场地点，对该行程进行重新规划排序。所有这些机票都属于一个从JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 出发。
说明:

• 如果存在多种有效的行程，你可以按字符自然排序返回最小的行程组合。例如，行程 [“JFK”, “LGA”] 与 [“JFK”, “LGB”] 相比就更小，排序更靠前
• 所有的机场都用三个大写字母表示（机场代码）。
• 假定所有机票至少存在一种合理的行程。

Example
示例 1:
输入: [[“MUC”, “LHR”], [“JFK”, “MUC”], [“SFO”, “SJC”], [“LHR”, “SFO”]]
输出: [“JFK”, “MUC”, “LHR”, “SFO”, “SJC”]

示例 2:
输入: [[“JFK”,”SFO”],[“JFK”,”ATL”],[“SFO”,”ATL”],[“ATL”,”JFK”],[“ATL”,”SFO”]]
输出: [“JFK”,”ATL”,”JFK”,”SFO”,”ATL”,”SFO”]
解释: 另一种有效的行程是 [“JFK”,”SFO”,”ATL”,”JFK”,”ATL”,”SFO”]。但是它自然排序更大更靠后。
Program
思路及算法
关键的地方在于如何表示已经访问过的边！
Hierholzer算法 用于在连通图中寻找欧拉路径，其流程如下：

• 从起点出发，进行深度优先搜索。
• 每次沿着某条边从某个顶点移动到另外一个顶点的时候，都需要删除这条边。
• 如果没有可移动的路径，则将所在节点加入到栈中，并返回。
  当我们顺序地考虑该问题时，我们也许很难解决该问题，因为我们无法判断当前节点的哪一个分支是「死胡同」分支。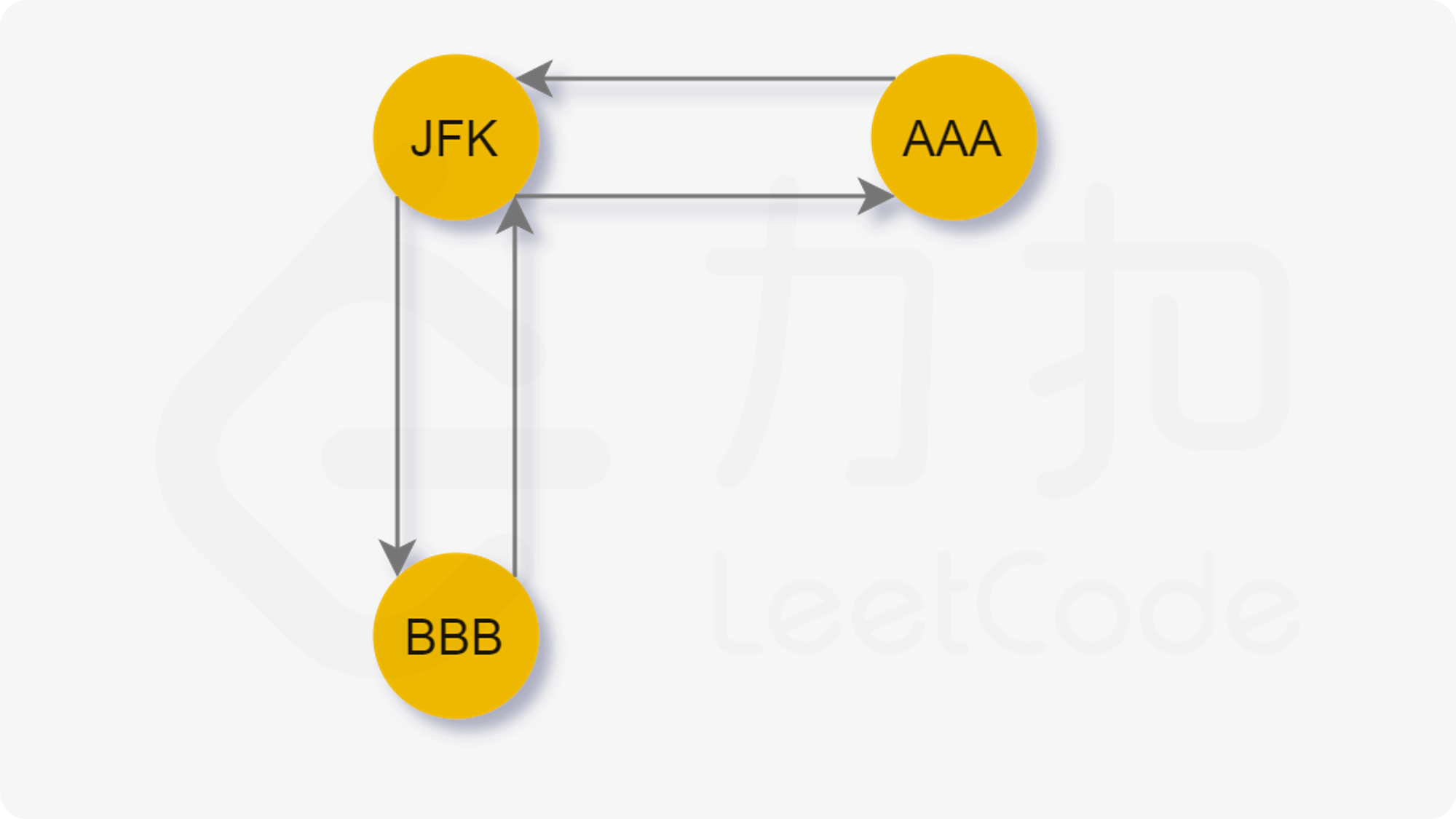
  
  不妨倒过来思考。我们注意到只有那个入度与出度差为 11、 的节点会导致死胡同。而该节点必然是最后一个遍历到的节点。我们可以改变入栈的规则，当我们遍历完一个节点所连的所有节点后，我们才将该节点入栈（即逆序入栈）。—— 这样就可以先将最后的路径进栈！得到的结果为逆序路径！可以发现了路径终点一定是入度比出度多1的节点！所以递归先入结果栈的肯定是终点。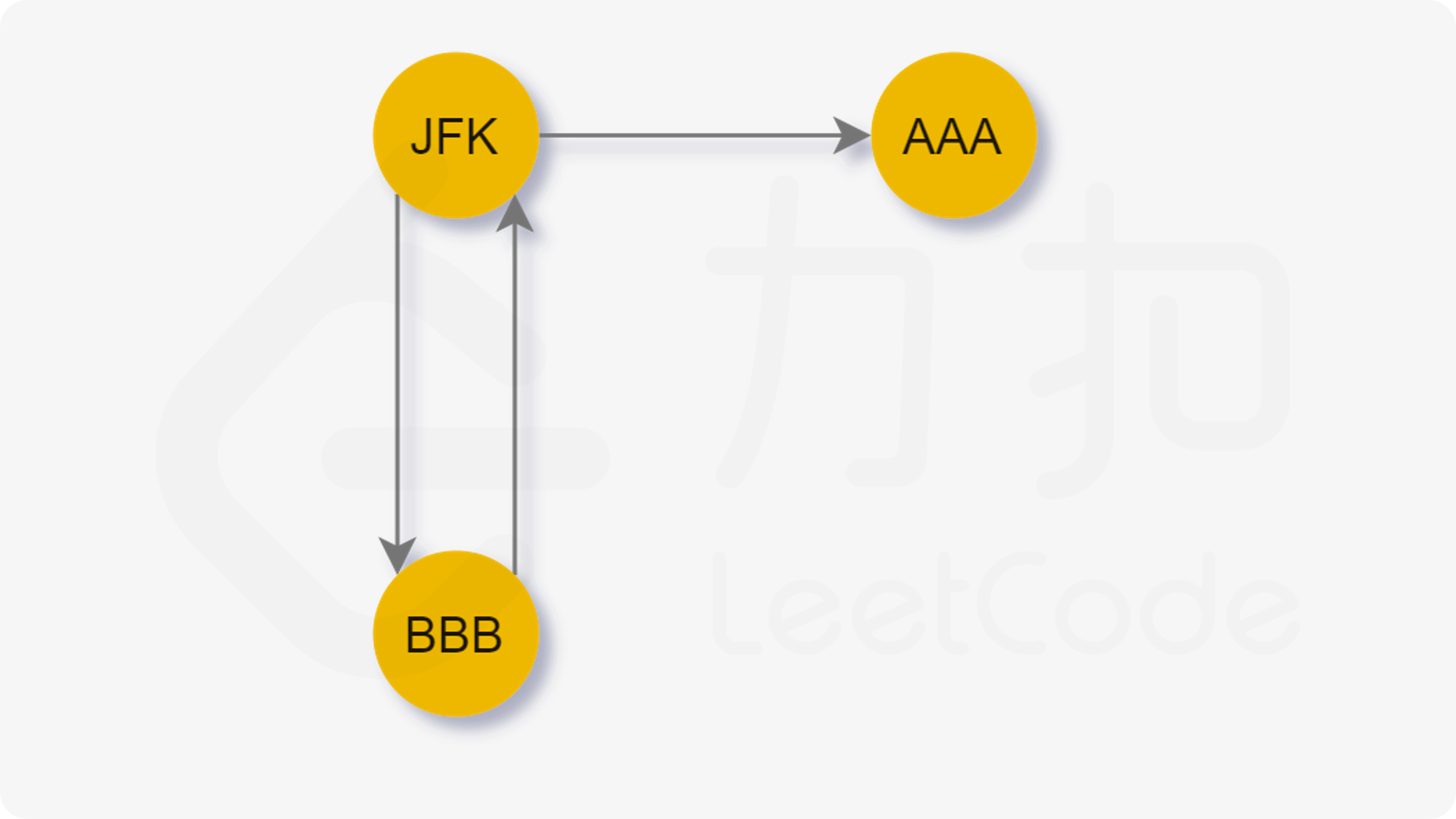
  
  对于当前节点而言，从它的每一个非「死胡同」分支出发进行深度优先搜索，都将会搜回到当前节点。而从它的「死胡同」分支出发进行深度优先搜索将不会搜回到当前节点。也就是说当前节点的死胡同分支将会优先于其他非「死胡同」分支入栈。

时间复杂度：$O(E\log{E})$，$E$为边数。
空间复杂度：$O(E)$，需要存储每条边

class Solution {
public:
    unordered_map<string, priority_queue<string, vector<string>, greater<string>>> Adj;
    vector<string> stk;
    void backtracking(const string& cur){
        while(Adj[cur].size()>0){
            string str=Adj[cur].top();
            Adj[cur].pop();
            backtracking(str);
        }
        stk.push_back(cur);
    }
    vector<string> findItinerary(vector<vector<string>>& tickets) {
        for(vector<string>& vec:tickets){
            Adj[vec[0]].push(vec[1]);
        }
        backtracking("JFK");
        reverse(stk.begin(), stk.end());
        return stk;
    }
};

Morris中序遍历

概念

Morris 中序遍历的一个重要步骤就是寻找当前节点的前驱节点，并且 Morris 中序遍历寻找下一个点始终是通过转移到right 指针指向的位置来完成的。

• 如果当前节点没有左子树，则遍历这个点，然后跳转到当前节点的右子树。
• 如果当前节点有左子树，那么它的前驱节点一定在左子树上，我们可以在左子树上一直向右行走，找到当前点的前驱节点。
• 如果前驱节点没有右子树，就将前驱节点的 right 指针指向当前节点。这一步是为了在遍历完前驱节点后能找到前驱节点的后继，也就是当前节点。
• 如果前驱节点的右子树为当前节点，说明前驱节点已经被遍历过并被修改了 \rm rightright 指针，这个时候我们重新将前驱的右孩子设置为空，遍历当前的点，然后跳转到当前节点的右子树。

  TreeNode* cur=root, *pre=NULL;
  while(cur!=NULL){
    if(cur->left==NULL){
      //print(cur->val); //已经达到左子树左端点
      cur=cur->right;
      continue
    }
    //寻找前驱节点
    pre=cur->left;
    while(pre->right!=NULL&&pre->right!=cur){ //有两种可能，第一种是第一次遍历该节点pre->right==NULL, 第二种是第二次遍历该节点，pre->right=cur
      pre=pre->right;
    }
    if(pre->right==NULL){ //第一次访问该节点
      pre->right=cur;
      cur=cur->left;
    }else{  //第二次访问该节点
      pre->right=NULL;
      //print(cur->val); //cur的左子树全部遍历完成
      cur=cur->right;
    }
  }

  501. 二叉搜索树中的众数

Description
给定一个有相同值的二叉搜索树（BST），找出 BST 中的所有众数（出现频率最高的元素）。

假定 BST 有如下定义：
结点左子树中所含结点的值小于等于当前结点的值
结点右子树中所含结点的值大于等于当前结点的值
左子树和右子树都是二叉搜索树
Example
例如：
给定 BST [1,null,2,2],

1
 \
  2
 /
2

返回[2].

提示：如果众数超过1个，不需考虑输出顺序
进阶：你可以不使用额外的空间吗？（假设由递归产生的隐式调用栈的开销不被计算在内）
Program

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int base, count ,maxCount;
    vector<int> res;
    void update(int x){
        if(x==base){
            count++;
        }else{
            base=x;
            count=1;
        }

        if(count==maxCount){
            res.push_back(base);
        }else if(count>maxCount){
            res.clear();
            maxCount=count;
            res.push_back(base);
        }
    }
    vector<int> findMode(TreeNode* root) {
        TreeNode* cur=root, *pre=NULL;
        while(cur!=NULL){ //Morris中序遍历，构造树的前驱
            if(cur->left==NULL){ //左节点为空没有前驱
                update(cur->val);
                cur=cur->right;
                continue;
            }
            //左子树为空，寻找前驱
            pre=cur->left;
            while(pre->right!=NULL&&pre->right!=cur){
                pre=pre->right;
            }
            if(pre->right==NULL){ //前驱右节点指向cur
                pre->right=cur;
                cur=cur->left;
            }else{  //恢复原树结构，前驱右指针置空
                pre->right=NULL;
                update(cur->val);
                cur=cur->right;
            }
        }
        return res;
    }
};

AC自动机

概念

struct Trie{
  bool isEnd;
  int cnt;
  Trie* next[26];
  Trie* fail;
  Trie(){
    isEnd=false;
    cnt=0;
    for(int i=0;i<26;i++) next[i]=NULL;
    fail=NULL;
  }
};
Trie* root=new Trie();
void insert(string str){
  int n=str.length();
  int idx=0;
  Trie* cur=root;
  while(idx<n){
    int pos=str[idx]-'a';
    if(cur->next[pos]==NULL) cur->next[pos]=new Trie();
    cur=cur->next[pos];
    idx++;
  }
  cur->isEnd=true;
  cur->cnt++;
}
void createFailPointer(){
  queue<Trie*> q;
  q.push(root);
  while(!q.empty()){
    Trie* cur=q.front();q.pop();
    Trie* fail=cur->fail;
    for(int i=0;i<26;i++){
      Trie* son=cur->next[i];
      if(son==NULL) {cur->next[i]=(fail==NULL?cur:fail.next[i]); continue;}
      son->fail=fail==NULL?cur:fail->next[i];
      q.push(son);
    }
  }
}
int ans=0;
int query(string str){
  int n=str.length();
  Trie* cur=root;
  for(int i=0;i<n;i++){
    int pos=str[i]-'s';
    Trie* son=cur->next[pos];
    while(son!=root&&son->cnt!=-1){
      ans+=son->cnt; son->cnt=-1;
      son=son->fail; //继续跳fail，因为fail是son的后缀
    }
    cur=cur->next[pos];
  }
  return ans;
}

面试题 17.17. 多次搜索

Description
给定一个较长字符串big和一个包含较短字符串的数组smalls，设计一个方法，根据smalls中的每一个较短字符串，对big进行搜索。输出smalls中的字符串在big里出现的所有位置positions，其中positions[i]为smalls[i]出现的所有位置。
Example
示例：
输入：
big = “mississippi”
smalls = [“is”,”ppi”,”hi”,”sis”,”i”,”ssippi”]
输出： [[1,4],[8],[],[3],[1,4,7,10],[5]]

提示：
0 <= len(big) <= 1000
0 <= len(smalls[i]) <= 1000
smalls的总字符数不会超过 100000。
你可以认为smalls中没有重复字符串。
所有出现的字符均为英文小写字母。
Program

**1、KMP**
KMP多次匹配问题
时间复杂度：$O(m*l+\sum_{i=1}^{l}{(n_i)})$，其中$l$为smalls数组长度，$n_i$为smalls数组第i个元素的长度；
空间复杂度：$O(\sum_{i=1}^{l}{(n_i)})$
```cpp
class Solution {
public:
    vector<int> getNext(string pattern){
        int n=pattern.length();
        vector<int> next(n, -1);
        int j=-1;
        for(int i=1;i<n;i++){
            while(j!=-1&&pattern[i]!=pattern[j+1]){
                j=next[j];
            }
            if(pattern[i]==pattern[j+1]) j++;
            next[i]=j;
        }
        return next;
    }
    vector<int> multiMatch(string text, string pattern){
        int m=text.length(), n=pattern.length();
        vector<int> next=getNext(pattern);
        vector<int> res;
        int j=-1;
        for(int i=0;i<m;i++){
            while(j!=-1&&text[i]!=pattern[j+1]){
                j=next[j];
            }
            if(text[i]==pattern[j+1]) j++;
            if(j==n-1){
                res.push_back(i-n+1);
                j=next[j];
            }
        }
        return res;
    }
    vector<vector<int>> multiSearch(string big, vector<string>& smalls) {
        vector<vector<int>> res;
        int n=smalls.size();
        for(int i=0;i<n;i++){
            if(smalls[i]==""){
                res.push_back({});
                continue;
            }
            res.push_back(multiMatch(big, smalls[i]));
        }
        return res;
    }
};

2、AC自动机

class Solution {
public:
    struct Trie{
        int cnt;
        Trie* fail;
        Trie* next[26];
        Trie(){
            cnt=0;
            fail=NULL;
            for(int i=0;i<26;i++) next[i]=NULL;
        }
    };
    Trie* root=new Trie();
    vector<vector<int>> res;
    void insert(string str, int i){
        int n=str.length();
        int idx=0;
        Trie* cur=root;
        while(idx<n){
            int pos=str[idx]-'a';
            if(cur->next[pos]==NULL) cur->next[pos]=new Trie();
            cur=cur->next[pos];
            idx++;
        }
        cur->cnt=i+1;
    }
    void createFailPointer(){
        queue<Trie*> q;
        q.push(root);
        while(!q.empty()){
            Trie* cur=q.front();q.pop();
            Trie* fail=cur->fail;
            for(int i=0;i<26;i++){
                Trie* son=cur->next[i];
                if(son==NULL) {cur->next[i]=(fail==NULL?cur:fail->next[i]);continue;} //孩子为空，调整指向
                son->fail=(fail==NULL?cur:fail->next[i]);
                q.push(son);
            }
        }
    }
    void query(string text, const vector<string>& smalls){
        int n=text.length();
        Trie* cur=root;
        for(int i=0;i<n;i++){
            int pos=text[i]-'a';
            Trie* son=cur->next[pos];
            while(son!=root){
                if(son->cnt>0){
                    int idx=son->cnt-1;
                    res[idx].push_back(i-smalls[idx].length()+1);
                }
                son=son->fail; //继续跳，因为fail也是son的后缀
            }
            cur=cur->next[pos];
        }
    }
    vector<vector<int>> multiSearch(string big, vector<string>& smalls) {
        int n=smalls.size();
        res.resize(n);
        for(int i=0;i<n;i++) insert(smalls[i], i);
        createFailPointer();
        query(big, smalls);
        return res;
    }
};

状态压缩DP

中心思想就是用二进制表示集合！

1755. 最接近目标值的子序列和

Description
给你一个整数数组 nums 和一个目标值 goal 。
你需要从 nums 中选出一个子序列，使子序列元素总和最接近 goal 。也就是说，如果子序列元素和为 sum ，你需要 最小化绝对差 abs(sum - goal) 。
返回 abs(sum - goal) 可能的 最小值 。
注意，数组的子序列是通过移除原始数组中的某些元素（可能全部或无）而形成的数组。
Example
示例 1：
输入：nums = [5,-7,3,5], goal = 6
输出：0
解释：选择整个数组作为选出的子序列，元素和为 6 。
子序列和与目标值相等，所以绝对差为 0 。

示例 2：
输入：nums = [7,-9,15,-2], goal = -5
输出：1
解释：选出子序列 [7,-9,-2] ，元素和为 -4 。
绝对差为 abs(-4 - (-5)) = abs(1) = 1 ，是可能的最小值。

示例 3：
输入：nums = [1,2,3], goal = -7
输出：7

提示：
$1 <= nums.length <= 40$
$-10^7 <= nums[i] <= 10^7$
$-10^9 <= goal <= 10^9$
Program
状压DP+二分
（1）首先，需要计算所有子序列的和sum[i]=sum[i-(1<<j)]+nums[j]，其中(i&(1<<j))!=0，状压DP！
（2）然后计算每个子序列和求abs(goal-s);
（3）然而，题目$n=40$，求子序列和时间复杂度：$O(n * 2^{n})$，超时，因为超过了$10^8$，但是$O(n * 2^{n/2})$可行；
（4）将数组分成前后各一半，分别求出前后的子序列和，最终答案只会出现在这三种情况：
① leftSum的某个;
② rightSum的某个;
③ leftSum与rightSum各一个的和！
（5）然而①②时间复杂度都是$O(\frac{n}{2})$，而③顺序遍历会是$O(n)$，还是超时；
（6）考虑二分，将leftSum,rightSum排序，那么：
i=0, j=rightSum.size()-1;
s=leftSum[i]+rightSum[j]
如果s比goal大，j减少，否则i增加！因为如果s大，那么j后面的与i求和都会比s大！，反之，如果s小，那么i前面的与j求和只会比s小；
时间复杂度:$(\log{\frac{n}{n}}+n * 2^{\frac{n}{2}})$

class Solution {
public:
    int minAbsDifference(vector<int>& nums, int goal) {
        int n=nums.size();
        int half=n/2;
        int ls=half, rs=n-half;
        vector<int> leftSum((1<<ls), 0), rightSum((1<<(rs)), 0);
        for(int i=1;i<(1<<ls);i++){
            for(int j=0;j<ls;j++){
                if((i&(1<<j))==0) continue;
                leftSum[i]=leftSum[i-(1<<j)]+nums[j];
                break;
            }
        }
        for(int i=1;i<(1<<rs);i++){
            for(int j=0;j<rs;j++){
                if((i&(1<<j))==0) continue;
                rightSum[i]=rightSum[i-(1<<j)]+nums[j+half];
                break;
            }
        }
        sort(leftSum.begin(), leftSum.end());
        sort(rightSum.begin(), rightSum.end());

        int res=INT_MAX;
        for(int x:leftSum) res=min(res, abs(goal-x));
        for(int x:rightSum) res=min(res, abs(goal-x));
        int i=0, j=rightSum.size()-1;
        while(i<leftSum.size()&&j>=0){
            int s=leftSum[i]+rightSum[j];
            res=min(res, abs(goal-s));
            if(s>goal) j--;
            else i++;
        }
        return res;
    }
};

526. 优美的排列

Description
假设有从 1 到 N 的 N 个整数，如果从这 N 个数字中成功构造出一个数组，使得数组的第 i 位 (1 <= i <= N) 满足如下两个条件中的一个，我们就称这个数组为一个优美的排列。条件：

第 i 位的数字能被 i 整除
i 能被第 i 位上的数字整除
现在给定一个整数 N，请问可以构造多少个优美的排列？
Example
示例1:
输入: 2
输出: 2
解释:
第 1 个优美的排列是 [1, 2]:
第 1 个位置（i=1）上的数字是1，1能被 i（i=1）整除
第 2 个位置（i=2）上的数字是2，2能被 i（i=2）整除

第 2 个优美的排列是 [2, 1]:
第 1 个位置（i=1）上的数字是2，2能被 i（i=1）整除
第 2 个位置（i=2）上的数字是1，i（i=2）能被 1 整除
说明:
N 是一个正整数，并且不会超过15。
Program

class Solution {
public:
    vector<bool> vis;
    int n;
    int ans=0;
    void dfs(int s){
        if(s==n){
            ans++;
            return;
        }
        for(int i=1;i<=n;i++){
            if(!vis[i]){
                if(((s+1)%i==0)||(i%(s+1)==0)){
                    vis[i]=true;
                    dfs(s+1);
                    vis[i]=false;
                }
            }
        }
    }
    int countArrangement(int N) {
        n=N;
        vis.resize(n+1, false);
        dfs(0);
        return ans;
    }
};

状态压缩DP
设DP[i]为排列i的个数，其中i用二进制表示，例如1011表示数1,2,4被使用:
令j为待排列的数字(1…N)，那么i中第j-1位必须为0表示未用，状态转移方程：
DP[i|(1<<(j-1))]+=DP[i]，当i的第j-1位未使用，且j与s成倍数关系（s为当前待排的第s个数）

class Solution {
public:
    int countArrangement(int N) {
        vector<int> DP(1<<N, 0);
        DP[0]=1;
        for(int i=0;i<(1<<N);i++){
            int s=0; //已经使用的个数
            for(int j=0;j<N;j++){
                s+=(i>>j)&1; //第j位是否为1,1表示使用，0表示未使用
            }
            s++;//正在使用的第s个数
            for(int j=1;j<=N;j++){ //遍历第s个数的可能值
                if(((i>>(j-1))&1)==0&&(j%s==0||s%j==0)){
                    DP[i|(1<<(j-1))]+=DP[i];
                }
            }
        }
        return DP[(1<<N)-1];
    }
};

滑窗技巧

[1,2,3,4,…, n]的和子数组和为$n * (n + 1) /2$
$ans=n+(n-1)+(n-2)+…+1$
可以通过滑窗移动的时候来求解：

int ans=0;
int end=-1;
for(int i=0;i<n;i++){
  ...
  while(end+1<n&&...){}
  ans+=end-i+1; //[1,2,3,4]以此[1],[1,2],[1,2,3],[1,2,3,4]的四个，[2,3,4]依次[2],[2,3],[2,3,4]的三个！
  ...
}

中缀表达式转后缀表达式

对于普通中缀表达式的计算，我们可以将其转化为后缀表达式再进行计算。转换方法也十分简单。只要建立一个用于存放运算符的栈，扫描该中缀表达式：

（1）如果遇到数字，直接将该数字输出到后缀表达式（以下部分用「输出」表示输出到后缀表达式）；
（2）如果遇到左括号，入栈；
（3）如果遇到右括号，不断输出栈顶元素，直至遇到左括号（左括号出栈，但不输出）；
（4）如果遇到其他运算符，不断去除所有运算优先级大于等于当前运算符的运算符，输出。（5）最后，新的符号入栈；
（6）把栈中剩下的符号依次输出，表达式转换结束。

位运算技巧

int lowbit(int x){  //求x最低位的1
  return x & (-x);
}

int setLowbitZero(int x){  //将x最低位置0
  return x & (x - 1);
}


int powerOftwo(int cap){ //返回大于等于cap的最小2次幂，
  int n = cap - 1; //如果cap就是2的幂次，cap - 1后，求得的是其右边所有置1 + 1，最终结果也是自己---cap！
  //将n的最高位1及其右边所有置1，最后结果+1就是所求
  n |= n >>> 1;
  n |= n >>> 2;
  n |= n >>> 4;
  n |= n >>> 8;
  n |= n >>> 16;
  return n < 0 ? 1 : (n >= (1 << 31))? 1 : n + 1;
}

a ^ b = c, a ^ c = b;

x = s, x = (x - 1) & s; //将s看作集合，1表示有，0表示没有，x求s的所有子集，例如1110，子集有1000,1100,1010,0110,...，0100,0010

跳表SkipList

图示

查找、插入、删除的时间复杂度都是$log{n}$，具体分析见参考文献

数据结构

nexts数组记录了该节点的层高对应的下一跳位置，nexts[i]表示第i层的下一跳；

struct Node{
    int val;
    int cnt; //重复元素个数
    vector<Node*> nexts; //节点层高，nexts[level]指向同一层level的下一个节点
    Node(int _val, int size){
        val = _val;
        cnt = 1;
        nexts.resize(size);
        for(int i = 0; i < size; i ++ ) nexts[i] = NULL;
    }
};

随机层高

对于插入的节点来说，其随机上升为索引，即随机层高，表明其作为第几层的索引。

int randLevel(){
    int level = 1;
    while(rand() % 2 == 0 && level < MAXLEVEL) level ++ ;
    return level;
}

找每层插入位置的前驱

Node* helper(Node* node, int level, int val){
    while(node -> nexts[level] != NULL && node -> nexts[level] -> val < val) node = node -> nexts[level];
    return node;
}

查找

bool find(int target, int num){ //查找元素，如果找到就增加数量
    Node * node = head;
    bool isPass = false;
    for(int i = curLevel - 1; i >= 0; i -- ){
        node = helper(node, i, target);
        if(node -> nexts[i] != NULL && node -> nexts[i] -> val == target){
            isPass = true;
            node -> nexts[i] -> cnt += num; ;
            break;
        }
    }
    return isPass;
}

插入

void add(int num) {
    if(find(num, 1)) return; //已存在

    //不存在，则需要插入
    int level = randLevel(); // 新节点随机上升的层高
    Node* node = head;
    Node* newNode = new Node(num, level);
    for(int i = curLevel - 1; i >= 0; i -- ){
        node = helper(node, i, num);
        if(i < level){
            Node* tmp = node -> nexts[i];
            node -> nexts[i] = newNode;
            newNode -> nexts[i] = tmp;
        }
    }
    if(level > curLevel){ //当前新增节点层高比跳表层数高
        for(int i = curLevel; i < level; i ++ ){
            head -> nexts[i] = newNode;
        }
        curLevel = level;
    }
}

删除

bool erase(int num) {
    Node* node = head;
    Node* delNode = NULL;
    bool isDel = false;
    for(int i = curLevel - 1; i >= 0; i -- ){
        node = helper(node, i, num);
        if(node -> nexts[i] != NULL && node -> nexts[i] -> val == num){
            if(!isDel){  //只删除一次
                node -> nexts[i] -> cnt --;
                isDel = true;
            }
            if(node -> nexts[i] -> cnt == 0){
                delNode = node -> nexts[i];
                node -> nexts[i] = node -> nexts[i] -> nexts[i];
            }
        }
    }
    if(delNode != NULL) delete delNode;
    for(int i = curLevel - 1; i >= 1; i -- ){ //检查跳表层数是否降低
        if(head -> nexts[i] == NULL){
            curLevel -- ;
        }
    }
    return isDel;
}

参考文献1
参考文献2

LeetCode 设计跳表

Description
不使用任何库函数，设计一个跳表。

跳表是在 O(log(n)) 时间内完成增加、删除、搜索操作的数据结构。跳表相比于树堆与红黑树，其功能与性能相当，并且跳表的代码长度相较下更短，其设计思想与链表相似。

跳表中有很多层，每一层是一个短的链表。在第一层的作用下，增加、删除和搜索操作的时间复杂度不超过 O(n)。跳表的每一个操作的平均时间复杂度是 O(log(n))，空间复杂度是 O(n)。

在本题中，你的设计应该要包含这些函数：
bool search(int target) : 返回target是否存在于跳表中。
void add(int num): 插入一个元素到跳表。
bool erase(int num): 在跳表中删除一个值，如果 num 不存在，直接返回false. 如果存在多个 num ，删除其中任意一个即可。
了解更多 : https://en.wikipedia.org/wiki/Skip_list

注意，跳表中可能存在多个相同的值，你的代码需要处理这种情况。
Example
样例:
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0); // 返回 false
skiplist.add(4);
skiplist.search(1); // 返回 true
skiplist.erase(0); // 返回 false，0 不在跳表中
skiplist.erase(1); // 返回 true
skiplist.search(1); // 返回 false，1 已被擦除
约束条件:
0 <= num, target <= 20000
最多调用 50000 次 search, add, 以及 erase操作。

Program

class Skiplist {
private:
    struct Node{
        int val;
        int cnt; //重复元素个数
        vector<Node*> nexts; //节点层高，nexts[level]指向同一层level的下一个节点
        Node(int _val, int size){
            val = _val;
            cnt = 1;
            nexts.resize(size);
            for(int i = 0; i < size; i ++ ) nexts[i] = NULL;
        }
    };
    //const int P = RAND_MAX / 4;
    const int MAXLEVEL = 16;
    int curLevel;
    Node* head;
    int randLevel(){
        int level = 1;
        while(rand() % 2 == 0 && level < MAXLEVEL) level ++ ;
        return level;
    }
    Node* helper(Node* node, int level, int val){
        while(node -> nexts[level] != NULL && node -> nexts[level] -> val < val) node = node -> nexts[level];
        return node;
    }
    bool find(int target, int num){ //查找元素，如果找到就增加数量
        Node * node = head;
        bool isPass = false;
        for(int i = curLevel - 1; i >= 0; i -- ){
            node = helper(node, i, target);
            if(node -> nexts[i] != NULL && node -> nexts[i] -> val == target){
                isPass = true;
                node -> nexts[i] -> cnt += num; ;
                break;
            }
        }
        return isPass;
    }
public:
    Skiplist() {
        curLevel = 0;
        head = new Node(-1, MAXLEVEL);
    }

    bool search(int target) {
        return find(target, 0);
    }

    void add(int num) {
        if(find(num, 1)) return; //已存在

        //不存在，则需要插入
        int level = randLevel(); // 新节点随机上升的层高
        Node* node = head;
        Node* newNode = new Node(num, level);
        for(int i = curLevel - 1; i >= 0; i -- ){
            node = helper(node, i, num);
            if(i < level){
                Node* tmp = node -> nexts[i];
                node -> nexts[i] = newNode;
                newNode -> nexts[i] = tmp;
            }
        }
        if(level > curLevel){ //当前新增节点层高比跳表层数高
            for(int i = curLevel; i < level; i ++ ){
                head -> nexts[i] = newNode;
            }
            curLevel = level;
        }
    }

    bool erase(int num) {
        Node* node = head;
        Node* delNode = NULL;
        bool isDel = false;
        for(int i = curLevel - 1; i >= 0; i -- ){
            node = helper(node, i, num);
            if(node -> nexts[i] != NULL && node -> nexts[i] -> val == num){
                if(!isDel){  //只删除一次
                    node -> nexts[i] -> cnt --;
                    isDel = true;
                }
                if(node -> nexts[i] -> cnt == 0){
                    delNode = node -> nexts[i];
                    node -> nexts[i] = node -> nexts[i] -> nexts[i];
                }
            }
        }
        if(delNode != NULL) delete delNode;
        for(int i = curLevel - 1; i >= 1; i -- ){ //检查跳表层数是否降低
            if(head -> nexts[i] == NULL){
                curLevel -- ;
            }
        }
        return isDel;
    }

    //有问题的插入
    // void add(int num) {
    //     int level = randLevel(); // 新节点随机上升的层高
    //     Node* node = head;
    //     Node* newNode = new Node(num, level);
    //     bool isInsert = false;
    //     bool isAdd = false;
    //     for(int i = curLevel - 1; i >= 0; i -- ){
    //         node = helper(node, i, num);
    //         if(i < level){ //有问题，比如3，刚开始存在，后面如果随机3的层高更高，指向会不同
    //             if(node -> nexts[i] != NULL && node -> nexts[i] -> val == num){ //已经重复
    //                 if(!isAdd){  //只加一次
    //                     node -> nexts[i] -> cnt ++ ;
    //                     isAdd = true;
    //                 }
    //             }else{
    //                 isInsert = true;
    //                 Node* tmp = node -> nexts[i];
    //                 node -> nexts[i] = newNode;
    //                 newNode -> nexts[i] = tmp;
    //             }  
    //         }
    //     }
    //     if(!isInsert && level == 0) isInsert = true;
    //     if(isInsert && level > curLevel){ //当前新增节点层高比跳表层数高
    //         for(int i = curLevel; i < level; i ++ ){
    //             head -> nexts[i] = newNode;
    //         }
    //         curLevel = level;
    //     }
    //     if(!isInsert) delete newNode;
    //     //cout <<"aaa";
    // }
};

/**
 * Your Skiplist object will be instantiated and called as such:
 * Skiplist* obj = new Skiplist();
 * bool param_1 = obj->search(target);
 * obj->add(num);
 * bool param_3 = obj->erase(num);
 */

赏

Thank you for inviting me to have candy.

支付宝

微信