PAT甲级

1001. A+B Format (20)

Calculate a + b and output the sum in standard format – that is, the digits must be separated into groups of three by commas (unless there are less than four digits).
Input
Each input file contains one test case. Each case contains a pair of integers a and b where -1000000 <= a, b <= 1000000. The numbers are separated by a space.
Output
For each test case, you should output the sum of a and b in one line. The sum must be written in the standard format.
Sample Input
-1000000 9
Sample Output
-999,991
Program

/*
根据题设数据范围，最多只输出两个逗号！~
*/
#include<iostream>
#include<vector>
#include<cmath>
using namespace std;
int main() {
	int A, B, sum = 0;
	vector<int> s;
	cin >> A >> B;
	sum = A + B;
	if (sum == 0) {
		cout << sum << endl;
		return 0;
	}
	if (sum < 0)
		cout << "-";
	sum = abs(sum);
	while (sum) {
			s.push_back(sum % 10);
			sum /= 10;
	}
	int flag = 0;
	vector<int>::iterator it;
	for (it = s.end()-1; it != s.begin(); it--) {
		cout << *it;
		flag++;
		if (flag == s.size()-3|| flag == s.size() - 6)
			cout << ",";
	}
	cout << *it<<endl;
	return 0;
}

#include<iostream>
#include<vector>
#include<cmath>
#include<cstring>
#include<string>
using namespace std;
int main() {
	int A, B, sum = 0;
	cin >> A >> B;
	sum = A + B;
	string str;
	str = to_string(sum);
	if (str[0] == '-')
	{
		cout << "-";
		str.erase(0, 1);
	}

	for (int i = 0; i < str.length(); i++)
	{
		cout << str[i];
		if (i == str.length() - 4||i==str.length()-7)
		{
			cout << ",";
		}
	}
	cout << endl;
	return 0;
}

1002. A+B for Polynomials (25)

This time, you are supposed to find A+B where A and B are two polynomials.
Input
Each input file contains one test case. Each case occupies 2 lines, and each line contains the information of a polynomial: K N1 aN1 N2 aN2 … NK aNK, where K is the number of nonzero terms in the polynomial, Ni and aNi (i=1, 2, …, K) are the exponents and coefficients, respectively. It is given that 1 <= K <= 10，0 <= NK < … < N2 < N1 <=1000.
Output
For each test case you should output the sum of A and B in one line, with the same format as the input. Notice that there must be NO extra space at the end of each line. Please be accurate to 1 decimal place.
Sample Input
2 1 2.4 0 3.2
2 2 1.5 1 0.5
Sample Output
3 2 1.5 1 2.9 0 3.2
Program

#include <iostream>  
#include <map>  
using namespace std;
int main()
{
	int k;
	map<int, double> Map;
	cin >> k;
    int n;
    double a;
	for (int i = 0; i < k; i++){
		cin >> n >> a;
		Map[n] += a;
	}
	cin >> k;
	for (int i = 0; i < k; i++){
		cin >> n >> a;
		Map[n] += a;
	}
	int sum = 0;
	for (int i = 0; i <=1000; i++){
		if (Map[i] == 0){
			continue;
		}
		sum++;
	}
	cout << sum;
	for (int i = 1000; i >= 0; i--){
		if (Map[i] != 0){
			cout << " "<<i<<" ";
			printf("%.1f", Map[i]);
		}
	}
	cout << endl;
	return 0;
}

#include <iostream>  
#include <map>  
using namespace std;
int main()
{
	int k;
	map<int, double> Map;
	cin >> k;
	for (int i = 0; i < k; i++)
	{
		double n, a;
		cin >> n >> a;
		Map[n] += a;
	}
	cin >> k;
	for (int i = 0; i < k; i++)
	{
		double n, a;
		cin >> n >> a;
		Map[n] += a;
	}
	int sum = 0;
	for (int i = 0; i <=1000; i++)
	{
		if (Map[i] == 0)
		{
			continue;
		}
		sum++;
	}
	cout << sum;
	for (int i = 1000; i >= 0; i--)
	{
		if (Map[i] != 0)
		{
			cout << " "<<i<<" ";
			printf("%.1f", Map[i]);
		}
	}
	cout << endl;
	return 0;
}

1003 Emergency（25）

As an emergency rescue team leader of a city, you are given a special map of your country. The map shows several scattered cities connected by some roads. Amount of rescue teams in each city and the length of each road between any pair of cities are marked on the map. When there is an emergency call to you from some other city, your job is to lead your men to the place as quickly as possible, and at the mean time, call up as many hands on the way as possible.
Input Specification
Each input file contains one test case. For each test case, the first line contains 4 positive integers: N (≤500) - the number of cities (and the cities are numbered from 0 to N−1), M - the number of roads, C1 and C2 - the cities that you are currently in and that you must save, respectively. The next line contains N integers, where the i-th integer is the number of rescue teams in the i-th city. Then M lines follow, each describes a road with three integers c1
​​ , c2 and L, which are the pair of cities connected by a road and the length of that road, respectively. It is guaranteed that there exists at least one path from C1 to C2.
Output Specification
For each test case, print in one line two numbers: the number of different shortest paths between C1 and C2, and the maximum amount of rescue teams you can possibly gather. All the numbers in a line must be separated by exactly one space, and there is no extra space allowed at the end of a line.
Sample Input
5 6 0 2
1 2 1 5 3
0 1 1
0 2 2
0 3 1
1 2 1
2 4 1
3 4 1
Sample Output
2 4
Program

#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
const int MAXV=501;
const int INF=0x3f3f3f3f;
int n,m,s,e;
int G[MAXV][MAXV];
bool bVis[MAXV];
int dist[MAXV];
int num[MAXV];
int weight[MAXV];
int w[MAXV];
void Dijkstra(int s){
	memset(dist,INF,sizeof(dist));
	memset(bVis,false,sizeof(bVis));
	memset(num,0,sizeof(num));
	memset(w,0,sizeof(w));
	w[s]=weight[s];
	num[s]=1;
	dist[s]=0;
	for(int i=0;i<n;i++){
		int u=-1,MIN=INF;
		for(int j=0;j<n;j++){
			if(!bVis[j]&&dist[j]<MIN){
				u=j;
				MIN=dist[j];
			}
		}
		if(u==-1) return;
		bVis[u]=true;
		for(int v=0;v<n;v++){
			if(!bVis[v]&&G[u][v]!=INF){
				if(dist[u]+G[u][v]<dist[v]){
					dist[v]=dist[u]+G[u][v];
					w[v]=w[u]+weight[v];
					num[v]=num[u];
				}else if(dist[u]+G[u][v]==dist[v]){
					num[v]+=num[u];
					if(w[u]+weight[v]>w[v]){
						w[v]=w[u]+weight[v];
					}
				}
			}
		}
	}
}
int main(){
	cin>>n>>m>>s>>e;
	for(int i=0;i<n;i++){
		cin>>weight[i];
	}
	memset(G,INF,sizeof(G));
	for(int i=0;i<m;i++){
		int s,e,l;
		cin>>s>>e>>l;
		G[s][e]=G[e][s]=l;
	}
	Dijkstra(s);
	cout<<num[e]<<" "<<w[e]<<endl;
	return 0;
}

#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
const int MAXV=501;
const int INF=0x3f3f3f3f;
int n,m,s,e;
struct Node{
	int v;
	int dis;
	Node(){}
	Node(int vv,int dd):v(vv),dis(dd){}
};
int dist[MAXV];
bool bVis[MAXV];
int num[MAXV];
int weight[MAXV];
int w[MAXV];
vector<Node> Adj[MAXV];
void Dijkstra(int s){
	memset(dist,INF,sizeof(dist));
	memset(bVis,false,sizeof(bVis));
	memset(num,0,sizeof(num));
	memset(w,0,sizeof(w));
	num[s]=1;
	w[s]=weight[s];
	dist[s]=0;
	for(int i=0;i<n;i++){
		int u=-1,MIN=INF;
		for(int j=0;j<n;j++){
			if(!bVis[j]&&dist[j]<MIN){
				u=j;
				MIN=dist[j];
			}
		}
		if(u==-1) return;
		bVis[u]=true;
		for(int j=0;j<Adj[u].size();j++){
			int v=Adj[u][j].v;
			int dis=Adj[u][j].dis;
			if(!bVis[v]){
				if(dist[u]+dis<dist[v]){
					dist[v]=dist[u]+dis;
					w[v]=w[u]+weight[v];
					num[v]=num[u];
				}else if(dist[u]+dis==dist[v]){
					num[v]+=num[u];
					if(w[u]+weight[v]>w[v]){
						w[v]=w[u]+weight[v];
					}
				}
			}
		}
	}
}
int main(){
	cin>>n>>m>>s>>e;
	for(int i=0;i<n;i++){
		cin>>weight[i];
	}
	for(int i=0;i<m;i++){
		int s,e,l;
		cin>>s>>e>>l;
		Adj[s].push_back(Node(e,l));
		Adj[e].push_back(Node(s,l));
	}
	Dijkstra(s);
	cout<<num[e]<<" "<<w[e]<<endl;
	return 0;
}

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int dis;
	Node(){}
	Node(int V,int Dis):v(V),dis(Dis){}
	bool operator < (const Node & tmp) const{
		return dis>tmp.dis;
	}
};
vector< vector<Node> > Adj;
vector<bool> vis;
vector<int> dist, team, num, teams;
int N,M,S,E;

struct Cmp{
	bool operator ()(const int &a, const int &b)const{
		return dist[a]>dist[b];
	}
};

void Dijkstra(int s){
	dist[s]=0;
	teams[s]=team[s];
	num[s]=1;
	priority_queue<int, vector<int>, Cmp> pq;
	pq.push(s);
	int nDone=0;
	while(nDone<N&&!pq.empty()){
		int u=pq.top();
		pq.pop();
		if(!vis[u]){
			vis[u]=true;
			nDone++;
		}else continue;
		for(int i=0;i<Adj[u].size();i++){
			int v=Adj[u][i].v;
			int dis=Adj[u][i].dis;
			if(!vis[v]){
				if(dist[u]+dis<dist[v]){
					dist[v]=dist[u]+dis;
					num[v]=num[u];
					teams[v]=teams[u]+team[v];
					pq.push(v);
				}else if(dist[u]+dis==dist[v]){
					num[v]+=num[u];
					if(teams[u]+team[v]>teams[v]) teams[v]=teams[u]+team[v];
				}
			}
		}
	}
}
int main(){
	cin>>N>>M>>S>>E;
	Adj.resize(N);
	vis.resize(N);
	dist.resize(N);
	team.resize(N);
	num.resize(N);
	teams.resize(N);
	fill(vis.begin(), vis.end(), false);
	fill(dist.begin(), dist.end(), INF);
	fill(num.begin(), num.end(), 0);
	fill(teams.begin(), teams.end(), 0);

	for(int i=0;i<N;i++) cin>>team[i];
	for(int i=0;i<M;i++){
		int u,v,l;
		cin>>u>>v>>l;
		Adj[u].push_back(Node(v, l));
		Adj[v].push_back(Node(u, l));
	}
	Dijkstra(S);
	cout<<num[E]<<" "<<teams[E]<<endl;
	return 0;
}

1004 Counting Leaves(30)

Description
A family hierarchy is usually presented by a pedigree tree. Your job is to count those family members who have no child.
Input Specification
Each input file contains one test case. Each case starts with a line containing 0<N<100, the number of nodes in a tree, and M (<N), the number of non-leaf nodes. Then M lines follow, each in the format:
ID K ID[1] ID[2] ... ID[K]
where ID is a two-digit number representing a given non-leaf node, K is the number of its children, followed by a sequence of two-digit ID’s of its children. For the sake of simplicity, let us fix the root ID to be 01.
The input ends with N being 0. That case must NOT be processed.
Output Specification
For each test case, you are supposed to count those family members who have no child for every seniority level starting from the root. The numbers must be printed in a line, separated by a space, and there must be no extra space at the end of each line.
The sample case represents a tree with only 2 nodes, where 01 is the root and 02 is its only child. Hence on the root 01 level, there is 0 leaf node; and on the next level, there is 1 leaf node. Then we should output 0 1 in a line.
Sample Input
2 1
01 1 02
Sample Output
0 1
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
struct Node{
	vector<int> child;
};
vector<Node> tree;
int N,M;
bool bFirst=true;
void layerOrder(int root){
	queue<int> q;
	int level=0;
	int levelSum=0;
	int leafSum=0;
	q.push(root);
	int sum=0;
	int start=0, end=1;
	while(!q.empty()){
		int now=q.front();
		q.pop();
		if(tree[now].child.size()==0){
			leafSum++;
		}else{
			for(int i=0;i<tree[now].child.size();i++){
				q.push(tree[now].child[i]);
				levelSum++;
			}
		}

		start++;
		if(start==end){
			start=0;
			end=levelSum;
			levelSum=0;
			if(bFirst) bFirst=false;
			else cout<<" ";
			cout<<leafSum;
			leafSum=0;
		}
	}
	cout<<endl;
}
int main(){
	cin>>N>>M;
	tree.resize(N+1);
	for(int i=0;i<M;i++){
		int id, k, idx;
		cin>>id>>k;
		for(int j=0;j<k;j++){
			cin>>idx;
			tree[id].child.push_back(idx);
		}
	}
	layerOrder(1);
	return 0;
}

1005 Spell It Right(20)

Description
Given a non-negative integer N, your task is to compute the sum of all the digits of N, and output every digit of the sum in English.
Input Specification
Each input file contains one test case. Each case occupies one line which contains an N (≤10100).
Output Specification
For each test case, output in one line the digits of the sum in English words. There must be one space between two consecutive words, but no extra space at the end of a line.
Sample Input
12345
Sample Output
one five
Program

#include<iostream>
#include<string>
#include<map>
#include<stack>
using namespace std;
//const char *x[] = {"zero","one","two","three","four","five","six","seven","eight","nine"};
int main() {
	string n;
	cin >> n;
	int sum=0;
	map<int, string> x;
	x[0] = "zero";
	x[1] = "one";
	x[2] = "two";
	x[3] = "three";
	x[4] = "four";
	x[5] = "five";
	x[6] = "six";
	x[7] = "seven";
	x[8] = "eight";
	x[9] = "nine";
	stack<string> s;
	for (unsigned int i = 0; i < n.length(); i++) {
		sum += n[i]-'0';
	}
	if (sum == 0) {
		cout << x[0] << endl;
		return 0;
	}

	while (sum) {
		s.push(x[sum % 10]);
		sum /= 10;
	}
	while (!s.empty()) {
		cout << s.top();
		if (s.size() != 1)
			cout << " ";
		s.pop();
	}
	cout << endl;
	return 0;
}

1006 Sign In and Sign Out(25)

Description
At the beginning of every day, the first person who signs in the computer room will unlock the door, and the last one who signs out will lock the door. Given the records of signing in’s and out’s, you are supposed to find the ones who have unlocked and locked the door on that day.
Input Specification
Each input file contains one test case. Each case contains the records for one day. The case starts with a positive integer M, which is the total number of records, followed by M lines, each in the format:
ID_number Sign_in_time Sign_out_time
where times are given in the format HH:MM:SS, and ID_number is a string with no more than 15 characters.
Output Specification
For each test case, output in one line the ID numbers of the persons who have unlocked and locked the door on that day. The two ID numbers must be separated by one space.
Note: It is guaranteed that the records are consistent. That is, the sign in time must be earlier than the sign out time for each person, and there are no two persons sign in or out at the same moment.
Sample Input
3
CS301111 15:30:28 17:00:10
SC3021234 08:00:00 11:25:25
CS301133 21:45:00 21:58:40
Sample Output
SC3021234 CS301133
Program

#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
using namespace std;
struct Node{
	string id;
	int h,m,s;
	Node(){}
	Node(string Id, int hh, int mm, int ss):id(Id),h(hh),m(mm),s(ss){}
	bool operator < (const Node &tmp) const{
		if(h!=tmp.h){
			return h<tmp.h;
		}else{
			if(m!=tmp.m){
				return m<tmp.m;
			}else{
				return s<tmp.s;
			}
		}
	}
};

int main(){
	int M;
	cin>>M;
	vector<Node> vec;
	vec.resize(M*2);
	for(int i=0;i<M;i++){
		cin>>vec[i].id;
		vec[i+M].id=vec[i].id;
		scanf("%2d:%2d:%2d %2d:%2d:%2d",
				&vec[i].h, &vec[i].m, &vec[i].s,
				&vec[i+M].h, &vec[i+M].m, &vec[i+M].s);
	}
	sort(vec.begin(),vec.end());
	cout<<vec[0].id<<" "<<vec[2*M-1].id<<endl;
	return 0;
}

1007 Maximum Subsequence Sum(25)

Description
Given a sequence of K integers { N1, N​2, …, N​K }. A continuous subsequence is defined to be { Ni, Ni+1, …, Nj } where 1≤i≤j≤K. The Maximum Subsequence is the continuous subsequence which has the largest sum of its elements. For example, given sequence { -2, 11, -4, 13, -5, -2 }, its maximum subsequence is { 11, -4, 13 } with the largest sum being 20.
Now you are supposed to find the largest sum, together with the first and the last numbers of the maximum subsequence.
Input Specification
Each input file contains one test case. Each case occupies two lines. The first line contains a positive integer K (≤10000). The second line contains K numbers, separated by a space.
Output Specification
For each test case, output in one line the largest sum, together with the first and the last numbers of the maximum subsequence. The numbers must be separated by one space, but there must be no extra space at the end of a line. In case that the maximum subsequence is not unique, output the one with the smallest indices i and j (as shown by the sample case). If all the K numbers are negative, then its maximum sum is defined to be 0, and you are supposed to output the first and the last numbers of the whole sequence.
Sample Input
10
-10 1 2 3 4 -5 -23 3 7 -21
Sample Output
10 1 4
Program

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int MAXV = 10000;
struct Node{
	int sum;
	int start;
	int end;
	Node(){}
	Node(int Sum, int Start, int End):sum(Sum),start(Start),end(End){}
};
int data[MAXV];
Node dp[MAXV];
int K;
int main(){
	cin>>K;
	for(int i=0;i<K;i++){
		cin>>data[i];
		dp[i].sum=data[i];
		dp[i].start=dp[i].end=i;
	}
	for(int i=1;i<K;i++){
		if(dp[i-1].sum+data[i]>data[i]){
			dp[i].sum=dp[i-1].sum+data[i];
			dp[i].start=dp[i-1].start;
			dp[i].end=i;
		}
	}
	int maxS=-1;
	int s=0,e=K-1;
	for(int i=0;i<K;i++){
		if(dp[i].sum>maxS){
			maxS=dp[i].sum;
			s=dp[i].start;
			e=dp[i].end;
		}
	}
	if(maxS==-1) maxS=0;
	cout<<maxS<<" "<<data[s]<<" "<<data[e]<<endl;
	return 0;
}

1008 Elevator(20)

Description
The highest building in our city has only one elevator. A request list is made up with N positive numbers. The numbers denote at which floors the elevator will stop, in specified order. It costs 6 seconds to move the elevator up one floor, and 4 seconds to move down one floor. The elevator will stay for 5 seconds at each stop.
For a given request list, you are to compute the total time spent to fulfill the requests on the list. The elevator is on the 0th floor at the beginning and does not have to return to the ground floor when the requests are fulfilled.
Input Specification
Each input file contains one test case. Each case contains a positive integer N, followed by N positive numbers. All the numbers in the input are less than 100.
Output Specification
For each test case, print the total time on a single line.
Sample Input
3 2 3 1
Sample Output
41
Program

#include<iostream>
using namespace std;
int main(){

	int n, a, t = 0, s = 0;
	cin >> n;
	for (int i = 0; i < n; i++){
		cin >> a;
		if (a > t) s += 6 * (a - t);///上
		else s += 4 * (t - a);///下
		s += 5;///停留时间
		t = a;
	}
	cout << s << endl;
	return 0;
}

1009 Product of Polynomials

Description
This time, you are supposed to find A×B where A and B are two polynomials.
Input Specification
Each input file contains one test case. Each case occupies 2 lines, and each line contains the information of a polynomial:
$K, N​1, a​_{N1}, N2, a_{N​2} … NK, a_{NK}$, where K is the number of nonzero terms in the polynomial, N​i and aNi(i=1,2,⋯,K) are the exponents and coefficients, respectively. It is given that 1≤K≤10, 0≤N​K<⋯<N2<N1≤1000.
Output Specification
For each test case you should output the product of A and B in one line, with the same format as the input. Notice that there must be NO extra space at the end of each line. Please be accurate up to 1 decimal place.
Sample Input
2 1 2.4 0 3.2
2 2 1.5 1 0.5
Sample Output
3 3 3.6 2 6.0 1 1.6
Program

#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
struct Poly{
	int exp;
	double coe;
}poly[1001];

double result[2001];
int main(){
	memset(result, 0, sizeof(result));
	int k1;
	cin>>k1;
	for(int i=0;i<k1;i++){
		cin>>poly[i].exp>>poly[i].coe;
	}
	int k2;
	cin>>k2;
	int exp;
	double coe;
	for(int i=0;i<k2;i++){
		cin>>exp>>coe;
		for(int j=0;j<k1;j++){
			result[exp+poly[j].exp] += coe*poly[j].coe;
		}
	}
	int num=0;
	for(int i=0;i<2001;i++){
		if(result[i]!=0) num++;
	}
	cout<<num;
	for(int i=2000;i>=0;i--){
		if(result[i]!=0){
			printf(" %d %.1f", i, result[i]);
		}
	}
	cout<<endl;
	return 0;
}

1010 Radix(25)

Description
Given a pair of positive integers, for example, 6 and 110, can this equation 6 = 110 be true? The answer is yes, if 6 is a decimal number and 110 is a binary number.
Now for any pair of positive integers N1 and N2, your task is to find the radix of one number while that of the other is given.
Input Specification
Each input file contains one test case. Each case occupies a line which contains 4 positive integers:
N1 N2 tag radix
Here N1 and N2 each has no more than 10 digits. A digit is less than its radix and is chosen from the set { 0-9, a-z } where 0-9 represent the decimal numbers 0-9, and a-z represent the decimal numbers 10-35. The last number radix is the radix of N1 if tag is 1, or of N2 if tag is 2.
Output Specification
For each test case, print in one line the radix of the other number so that the equation N1 = N2 is true. If the equation is impossible, print Impossible. If the solution is not unique, output the smallest possible radix.
Sample Input 1
6 110 1 10
Sample Output 1
2
Sample Input 2
1 ab 1 2
Sample Output 2
Impossible
Program

/*
radix不会超过int范围
而N1不会超过long long范围！
所以如果N2溢出了long long只需判断负即可
*/
#include<iostream>
#include<cstring>
#include<map>
#include<algorithm>
using namespace std;
long long one=1;
const long long INF=(one<<63)-1;
int tag, radix;
string N1, N2;
map<char, int> m;
void init(){
	for(char ch='0';ch<='9';ch++){
		m[ch]=ch-'0';
	}
	for(char ch='a';ch<='z';ch++){
		m[ch]=ch-'a'+10;
	}
}
long long convertRadix10(string n, long long radix, long long x){
	long long result=0;
	for(int i=0;i<n.length();i++){
		result=result*radix+m[n[i]];
		if(result<0||result>x) return -1;
	}
	return result;
}
int findLargestDigit(string n){
	int result=0;
	for(int i=0;i<n.length();i++){
		result=max(result, m[n[i]]);
	}
	return result+1;
}
int cmp(string n, long long radix, long long x){
	long long result=convertRadix10(n, radix, x);
	if(result==-1) return 1;
	if(x>result) return -1;
	else return 0;
}
long long binarySearch(string n,long long x, long long left, long long right){
	while(left<=right){
		long long mid=(left+right)/2;
		int flag=cmp(n, mid, x);
		if(flag==0) return mid;
		else if(flag==1) right=mid-1;
		else left=mid+1;
	}
	return -1;
}
int main(){
	init();
	cin>>N1>>N2>>tag>>radix;
	if(tag==2) swap(N1, N2);
	long long x1=convertRadix10(N1, radix, INF);
	long long low=findLargestDigit(N2);
	long long high=max(x1, low);
	long long result=binarySearch(N2, x1, low, high);
	if(result==-1) cout<<"Impossible"<<endl;
	else cout<<result<<endl;
	return 0;
}

1011 World Cup Betting(20)

Description
With the 2010 FIFA World Cup running, football fans the world over were becoming increasingly excited as the best players from the best teams doing battles for the World Cup trophy in South Africa. Similarly, football betting fans were putting their money where their mouths were, by laying all manner of World Cup bets.
Chinese Football Lottery provided a “Triple Winning” game. The rule of winning was simple: first select any three of the games. Then for each selected game, bet on one of the three possible results – namely W for win, T for tie, and L for lose. There was an odd assigned to each result. The winner’s odd would be the product of the three odds times 65%.
For example, 3 games’ odds are given as the following:
W T L
1.1 2.5 1.7
1.2 3.1 1.6
4.1 1.2 1.1
To obtain the maximum profit, one must buy W for the 3rd game, T for the 2nd game, and T for the 1st game. If each bet takes 2 yuans, then the maximum profit would be (4.1×3.1×2.5×65%−1)×2=39.31 yuans (accurate up to 2 decimal places).
Input Specification
Each input file contains one test case. Each case contains the betting information of 3 games. Each game occupies a line with three distinct odds corresponding to W, T and L.
Output Specification
For each test case, print in one line the best bet of each game, and the maximum profit accurate up to 2 decimal places. The characters and the number must be separated by one space.
Sample Input
1.1 2.5 1.7
1.2 3.1 1.6
4.1 1.2 1.1
Sample Output
T T W 39.31
Program

#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
const char ch[3]={'W','T','L'};
int main(){
	double result=0.65;
	for(int i=0;i<3;i++){
		double maxT=0.0;
		int index=0;
		for(int j=0;j<3;j++){
			double tmp;
			cin>>tmp;
			if(tmp>maxT){
				maxT=tmp;
				index=j;
			}
		}

		result*=maxT;
		if(i!=0) cout<<" ";
		cout<<ch[index];
		if(i==2) printf(" %.2f\n", result*2-2);
	}
	return 0;
}

1012 The Best Rank(25)

Description
To evaluate the performance of our first year CS majored students, we consider their grades of three courses only: C - C Programming Language, M - Mathematics (Calculus or Linear Algrbra), and E - English. At the mean time, we encourage students by emphasizing on their best ranks – that is, among the four ranks with respect to the three courses and the average grade, we print the best rank for each student.
For example, The grades of C, M, E and A - Average of 4 students are given as the following:
StudentID C M E A
310101 98 85 88 90
310102 70 95 88 84
310103 82 87 94 88
310104 91 91 91 91
Then the best ranks for all the students are No.1 since the 1st one has done the best in C Programming Language, while the 2nd one in Mathematics, the 3rd one in English, and the last one in average.
Input Specification
Each input file contains one test case. Each case starts with a line containing 2 numbers N and M (≤2000), which are the total number of students, and the number of students who would check their ranks, respectively. Then N lines follow, each contains a student ID which is a string of 6 digits, followed by the three integer grades (in the range of [0, 100]) of that student in the order of C, M and E. Then there are M lines, each containing a student ID.
Output Specification
For each of the M students, print in one line the best rank for him/her, and the symbol of the corresponding rank, separated by a space.
The priorities of the ranking methods are ordered as A > C > M > E. Hence if there are two or more ways for a student to obtain the same best rank, output the one with the highest priority.
If a student is not on the grading list, simply output N/A.
Sample Input
5 6
310101 98 85 88
310102 70 95 88
310103 82 87 94
310104 91 91 91
310105 85 90 90
310101
310102
310103
310104
310105
999999
Sample Output
1 C
1 M
1 E
1 A
3 A
N/A
Program

#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
#include<algorithm>
#include<set>
#include<map>
using namespace std;
int cmpIndex=3;
struct Node{
	string id;
	int grade[4];
	int rank[4];
	Node(){}
	Node(string Id, int C, int M, int E):id(Id){
		grade[1]=C;
		grade[2]=M;
		grade[3]=E;
		grade[0]=floor((grade[1]+grade[2]+grade[3])/3.0+0.5);
	}
	bool operator < (const Node &tmp) const{
		return grade[cmpIndex]>tmp.grade[cmpIndex];
	}
};
char course[]={'A','C','M','E'};
vector<Node> vec;
set<string> s;
map<string, int> m;
int N,M;
int main(){
	cin>>N>>M;

	string id;
	for(int i=0;i<N;i++){
		string id;
		int C,M,E;
		cin>>id>>C>>M>>E;
		s.insert(id);
		vec.push_back(Node(id,C,M,E));
	}
	for(cmpIndex=0;cmpIndex<4;cmpIndex++){
		sort(vec.begin(),vec.end());
		vec[0].rank[cmpIndex]=1;
		if(cmpIndex==3) m[vec[0].id]=0;
		for(int i=1;i<N;i++){
			if(vec[i].grade[cmpIndex]==vec[i-1].grade[cmpIndex]){
				vec[i].rank[cmpIndex]=vec[i-1].rank[cmpIndex];
			}else{
				vec[i].rank[cmpIndex]=i+1;
			}
			if(cmpIndex==3) m[vec[i].id]=i;
		}
	}
	string queryId;
	for(int i=0;i<M;i++){
		cin>>queryId;
		if(s.find(queryId)==s.end()){
			cout<<"N/A"<<endl;
		}else{
			int minIndex=0;
			int minRank=vec[m[queryId]].rank[minIndex];
			for(int j=1;j<4;j++){
				if(minRank>vec[m[queryId]].rank[j]){
					minRank=vec[m[queryId]].rank[j];
					minIndex=j;
				}
			}
			cout<<minRank<<" "<<course[minIndex]<<endl;
		}
	}
	return 0;
}

1013 Battle Over Cities(25)

Description
It is vitally important to have all the cities connected by highways in a war. If a city is occupied by the enemy, all the highways from/toward that city are closed. We must know immediately if we need to repair any other highways to keep the rest of the cities connected. Given the map of cities which have all the remaining highways marked, you are supposed to tell the number of highways need to be repaired, quickly.
For example, if we have 3 cities and 2 highways connecting city1-city2​​ and city1-city3. Then if city1 is occupied by the enemy, we must have 1 highway repaired, that is the highway city2-city3.
Input Specification
Each input file contains one test case. Each case starts with a line containing 3 numbers N (<1000), M and K, which are the total number of cities, the number of remaining highways, and the number of cities to be checked, respectively. Then M lines follow, each describes a highway by 2 integers, which are the numbers of the cities the highway connects. The cities are numbered from 1 to N. Finally there is a line containing K numbers, which represent the cities we concern.
Output Specification
For each of the K cities, output in a line the number of highways need to be repaired if that city is lost.
Sample Input
3 2 3
1 2
1 3
1 2 3
Sample Output
1
0
0
Program

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
const int MAXN=1001;
vector< vector<int> > vec;
int N,M,K;
int sum;
bool vis[MAXN];
int num;
void DFS(int i){
	vis[i]=true;
	sum++;
	for(int j=0;j<vec[i].size();j++){
		int v=vec[i][j];
		if(!vis[v]) DFS(v);
	}
}
void DFSTraverse(){
	for(int i=1;i<=N;i++){
		if(!vis[i]){
			DFS(i);
			if(sum!=N-1) num++;
		}
	}

}

int main(){
	scanf("%d%d%d", &N,&M,&K);
	vec.resize(N+1);
	for(int i=0;i<M;i++){
		int a,b;
		scanf("%d%d", &a, &b);
		vec[a].push_back(b);
		vec[b].push_back(a);
	}

	for(int i=0;i<K;i++){
		sum=0;
		num=0;
		fill(vis, vis+MAXN, false);
		int tmp;
		scanf("%d", &tmp);
		vis[tmp]=true;
		DFSTraverse();
		printf("%d\n", num);
	}

	return 0;
}

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
const int MAXN=1001;
vector< vector<int> > vec;
int N,M,K;
int father[MAXN];
bool vis[MAXN];
int findFather(int x){
	if(x!=father[x]){
		father[x]=findFather(father[x]);
	}
	return father[x];
}
void unionSet(int a,int b){
	int fa=findFather(a);
	int fb=findFather(b);
	if(fa!=fb) father[fa]=fb;
}
int main(){
	scanf("%d%d%d", &N,&M,&K);
	vec.resize(N+1);
	for(int i=0;i<M;i++){
		int a,b;
		scanf("%d%d", &a, &b);
		vec[a].push_back(b);
		vec[b].push_back(a);
	}
	for(int i=0;i<K;i++){
		int tmp;
		scanf("%d", &tmp);
		for(int i=1;i<=N;i++) father[i]=i;
		fill(vis, vis+MAXN,false);
		for(int j=1;j<=N;j++){
			for(int k=0;k<vec[j].size();k++){
				int v=vec[j][k];
				if(j==tmp||v==tmp) continue;
				unionSet(j, v);
			}
		}
		int sum=0;
		for(int i=1;i<=N;i++){
			if(i==tmp) continue;
			int fa=findFather(i);
			if(!vis[fa]){
				vis[fa]=true;
				sum++;
			}
		}
		printf("%d\n", sum-1);
	}
	return 0;
}

1014 Waiting in Line(30)

Description
Suppose a bank has N windows open for service. There is a yellow line in front of the windows which devides the waiting area into two parts. The rules for the customers to wait in line are:
The space inside the yellow line in front of each window is enough to contain a line with M customers. Hence when all the N lines are full, all the customers after (and including) the (NM+1)st one will have to wait in a line behind the yellow line.
Each customer will choose the shortest line to wait in when crossing the yellow line. If there are two or more lines with the same length, the customer will always choose the window with the smallest number.
$Customer_i$ will take $T_i$ minutes to have his/her transaction processed.The first N customers are assumed to be served at 8:00am.
Now given the processing time of each customer, you are supposed to tell the exact time at which a customer has his/her business done.
For example, suppose that a bank has 2 windows and each window may have 2 custmers waiting inside the yellow line. There are 5 customers waiting with transactions taking 1, 2, 6, 4 and 3 minutes, respectively. At 08:00 in the morning, customer1 is served at window1 while customer2 is served at window2. Customer3 will wait in front of window​1 and customer4 will wait in front of window2. Customer5 will wait behind the yellow line.
At 08:01, customer1 is done and customer5 enters the line in front of window1 since that line seems shorter now. Customer2 will leave at 08:02, customer4 at 08:06, customer​3 at 08:07, and finally customer5 at 08:10.
Input Specification
Each input file contains one test case. Each case starts with a line containing 4 positive integers: N (≤20, number of windows), M (≤10, the maximum capacity of each line inside the yellow line), K (≤1000, number of customers), and Q (≤1000, number of customer queries).
The next line contains K positive integers, which are the processing time of the K customers.
The last line contains Q positive integers, which represent the customers who are asking about the time they can have their transactions done. The customers are numbered from 1 to K.
Output Specification
For each of the Q customers, print in one line the time at which his/her transaction is finished, in the format HH:MM where HH is in [08, 17] and MM is in [00, 59]. Note that since the bank is closed everyday after 17:00, for those customers who cannot be served before 17:00, you must output Sorry instead.
Sample Input
2 2 7 5
1 2 6 4 3 534 2
3 4 5 6 7
Sample Output
08:07
08:06
08:10
17:00
Sorry
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int MAXK=1001;
const int INF=0x3f3f3f3f;
int n,m,k,query,q;
int convertToMinute(int h, int m){
	return h*60+m;
}
struct Window{
	int endTime, popTime;
	queue<int> q;
}window[20];
int ans[MAXK], needTime[MAXK];
int main(){
	cin>>n>>m>>k>>query;
	for(int i=0;i<k;i++) cin>>needTime[i];
	int sTime=convertToMinute(8, 0);
	int eTime=convertToMinute(17,0);
	for(int i=0;i<n;i++) window[i].popTime=window[i].endTime=sTime;
	int inIndex=0;
	for(int i=0;i<min(n*m, k);i++){
		window[inIndex%n].q.push(inIndex);
		window[inIndex%n].endTime+=needTime[inIndex];
		if(inIndex<n)window[inIndex%n].popTime=needTime[inIndex];
		ans[inIndex]=window[inIndex%n].endTime;
		inIndex++;
	}
	for(;inIndex<k;inIndex++){
		int idx=-1, minPopTime=INF;
		for(int i=0;i<n;i++){
			if(window[i].popTime<minPopTime){
				idx=i;
				minPopTime=window[i].popTime;
			}
		}
		Window& w=window[idx];
		w.q.pop();
		w.q.push(inIndex);
		w.endTime+=needTime[inIndex];
		w.popTime+=needTime[w.q.front()];
		ans[inIndex]=w.endTime;
	}
	for(int i=0;i<query;i++){
		int idx;
		cin>>idx;
		if(ans[idx-1]-needTime[idx-1]>=eTime) cout<<"Sorry"<<endl;
		else printf("%02d:%02d\n",ans[idx-1]/60,ans[idx-1]%60);
	}
	return 0;
}

1015 Reversible Primes(20)

Description
A reversible prime in any number system is a prime whose “reverse” in that number system is also a prime. For example in the decimal system 73 is a reversible prime because its reverse 37 is also a prime.
Now given any two positive integers N (<$10^{​5}$) and D (1<D≤10), you are supposed to tell if N is a reversible prime with radix D.
Input Specification
The input file consists of several test cases. Each case occupies a line which contains two integers N and D. The input is finished by a negative N.
Output Specification
For each test case, print in one line Yes if N is a reversible prime with radix D, or No if not.
Sample Input
73 10
23 2
23 10
-2
Sample Output
Yes
Yes
No
Program

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
bool isPrime(int x){
	if(x<=1) return false;
	for(int i=2;i*i<=x;i++){
		if(x%i==0) return false;
	}
	return true;
}
vector<int> vec;
int n, radix;
int main(){
	while(cin>>n&&n>=0){
		cin>>radix;
		vec.clear();
		if(!isPrime(n)) cout<<"No"<<endl;
		else{
			while(n!=0){
				vec.push_back(n%radix);
				n/=radix;
			}
			for(int i=0;i<vec.size();i++){
				n=n*radix+vec[i];
			}
			if(isPrime(n)) cout<<"Yes"<<endl;
			else cout<<"No"<<endl;
		}
	}
	return 0;
}

1016 Phone Bills(25)

Description
A long-distance telephone company charges its customers by the following rules:
Making a long-distance call costs a certain amount per minute, depending on the time of day when the call is made. When a customer starts connecting a long-distance call, the time will be recorded, and so will be the time when the customer hangs up the phone. Every calendar month, a bill is sent to the customer for each minute called (at a rate determined by the time of day). Your job is to prepare the bills for each month, given a set of phone call records.
Input Specification
Each input file contains one test case. Each case has two parts: the rate structure, and the phone call records.
The rate structure consists of a line with 24 non-negative integers denoting the toll (cents/minute) from 00:00 - 01:00, the toll from 01:00 - 02:00, and so on for each hour in the day.
The next line contains a positive number N (≤1000), followed by N lines of records. Each phone call record consists of the name of the customer (string of up to 20 characters without space), the time and date (mm:dd:hh:mm), and the word on-line or off-line.
For each test case, all dates will be within a single month. Each on-line record is paired with the chronologically next record for the same customer provided it is an off-line record. Any on-line records that are not paired with an off-line record are ignored, as are off-line records not paired with an on-line record. It is guaranteed that at least one call is well paired in the input. You may assume that no two records for the same customer have the same time. Times are recorded using a 24-hour clock.
Output Specification
For each test case, you must print a phone bill for each customer.
Bills must be printed in alphabetical order of customers’ names. For each customer, first print in a line the name of the customer and the month of the bill in the format shown by the sample. Then for each time period of a call, print in one line the beginning and ending time and date (dd:hh:mm), the lasting time (in minute) and the charge of the call. The calls must be listed in chronological order. Finally, print the total charge for the month in the format shown by the sample.
Sample Input

10 10 10 10 10 10 20 20 20 15 15 15 15 15 15 15 20 30 20 15 15 10 10 10
10
CYLL 01:01:06:01 on-line
CYLL 01:28:16:05 off-line
CYJJ 01:01:07:00 off-line
CYLL 01:01:08:03 off-line
CYJJ 01:01:05:59 on-line
aaa 01:01:01:03 on-line
aaa 01:02:00:01 on-line
CYLL 01:28:15:41 on-line
aaa 01:05:02:24 on-line
aaa 01:04:23:59 off-line

Sample Output

CYJJ 01
01:05:59 01:07:00 61 $12.10
Total amount: $12.10
CYLL 01
01:06:01 01:08:03 122 $24.40
28:15:41 28:16:05 24 $3.85
Total amount: $28.25
aaa 01
02:00:01 04:23:59 4318 $638.80
Total amount: $638.80

Program

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
#include<queue>
using namespace std;
int rate[24];
int sumDay=0;
int n;
struct Node{
	string name;
	int month, day, hour, minute;
	bool status;
	bool operator < (const Node &tmp) const{
		if(name!=tmp.name){
			return name<tmp.name;
		}else if(month!=tmp.month){
			return month<tmp.month;
		}else if(day!=tmp.day){
			return day<tmp.day;
		}else if(hour!=tmp.hour){
			return hour<tmp.hour;
		}else{
			return minute<tmp.minute;
		}
	}

};
vector<Node> vec;
int calTime(Node a, Node b){
	int aa=a.day*24*60+a.hour*60+a.minute;
	int bb=b.day*24*60+b.hour*60+b.minute;
	return bb-aa;
}
int calCosNode(Node a){
	int sum=(a.day-1)*sumDay;
	for(int hour=0;hour<a.hour;hour++){
		sum+=rate[hour]*60;
	}
	sum+=a.minute*rate[a.hour];
	return sum;
}
int calCos(Node a, Node b){
	int bb=calCosNode(b);
	int aa=calCosNode(a);
	return bb-aa;
}
int main(){
	for(int i=0;i<24;i++){
		cin>>rate[i];
		sumDay+=rate[i];
	}
	sumDay*=60;
	cin>>n;
	vec.resize(n);
	for(int i=0;i<n;i++){
		string tmp;
		cin>>vec[i].name;
		scanf("%d:%d:%d:%d",
			  &vec[i].month,&vec[i].day,
			  &vec[i].hour,&vec[i].minute);
		cin>>tmp;
		if(tmp=="on-line") vec[i].status=true;
		else vec[i].status=false;
	}
	sort(vec.begin(),vec.end());

	int index=0;
	int sum=0.0;
	bool isFirst=true;
	string preName;
	while(index<=n-2){
		Node pre=vec[index];
		Node next=vec[index+1];
		if(pre.name==next.name){
			if(pre.status==1&&next.status==0){
				if(isFirst){
					preName=pre.name;
					cout<<pre.name;
					printf(" %02d\n", pre.month);
					isFirst=false;
				}else if(pre.name!=preName){
					printf("Total amount: $%.2f\n",sum/100.0);
					sum=0;
					preName=pre.name;
					cout<<pre.name;
					printf(" %02d\n", pre.month);
				}
				int time=calTime(pre, next);
				int cos=calCos(pre, next);
				printf("%02d:%02d:%02d %02d:%02d:%02d %d $%.2f\n",
					  pre.day,pre.hour,pre.minute,
					  next.day,next.hour,next.minute,
					  time,cos/100.0);
				sum+=cos;
				index+=2;
			}else{
				index++;
			}
		}else{
			index++;
		}
	}
	if(sum!=0){
		printf("Total amount: $%.2f\n",sum/100.0);
	}
	return 0;
}

1017 Queueing at Bank(25)

Description
Suppose a bank has K windows open for service. There is a yellow line in front of the windows which devides the waiting area into two parts. All the customers have to wait in line behind the yellow line, until it is his/her turn to be served and there is a window available. It is assumed that no window can be occupied by a single customer for more than 1 hour.
Now given the arriving time T and the processing time P of each customer, you are supposed to tell the average waiting time of all the customers.
Input Specification
Each input file contains one test case. For each case, the first line contains 2 numbers: N ($≤10^{4}$) - the total number of customers, and K (≤100) - the number of windows. Then N lines follow, each contains 2 times: HH:MM:SS - the arriving time, and P - the processing time in minutes of a customer. Here HH is in the range [00, 23], MM and SS are both in [00, 59]. It is assumed that no two customers arrives at the same time.
Notice that the bank opens from 08:00 to 17:00. Anyone arrives early will have to wait in line till 08:00, and anyone comes too late (at or after 17:00:01) will not be served nor counted into the average.
Output Specification
For each test case, print in one line the average waiting time of all the customers, in minutes and accurate up to 1 decimal place.
Sample Input
7 3
07:55:00 16
17:00:01 2
07:59:59 15
08:01:00 60
08:00:00 30
08:00:02 2
08:03:00 10
Sample Output
8.2
Program

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int K=111;
const int INF=0x3f3f3f3f;
struct Customer{
	int comeTime;
	int serveTime;
}newCustomer;
vector<Customer> custom;
int convertTime(int h, int m, int s){
	return h*3600+m*60+s;
}
bool cmp(Customer a, Customer b){
	return a.comeTime<b.comeTime;
}
int endTime[K];
int main(){
	int c,w, totTime=0;
	int stTime=convertTime(8, 0, 0);
	int edTime=convertTime(17, 0, 0);
	cin>>c>>w;
	for(int i=0;i<w;i++) endTime[i]=stTime;
	for(int i=0;i<c;i++){
		int h,m,s,serveTime;
		scanf("%d:%d:%d %d", &h, &m, &s, &serveTime);
		int comeTime=convertTime(h, m, s);
		if(comeTime>edTime) continue;
		newCustomer.comeTime=comeTime;
		newCustomer.serveTime=serveTime<=60?serveTime*60:3600;
		custom.push_back(newCustomer);
	}
	sort(custom.begin(), custom.end(), cmp);
	for(int i=0;i<custom.size();i++){
		int idx=-1, minEndTime=INF;
		for(int j=0;j<w;j++){
			if(endTime[j]<minEndTime){
				minEndTime=endTime[j];
				idx=j;
			}
		}
		if(endTime[idx]<=custom[i].comeTime){
			endTime[idx]=custom[i].comeTime+custom[i].serveTime;
		}else{
			totTime+=(endTime[idx]-custom[i].comeTime);
			endTime[idx]+=custom[i].serveTime;
		}
	}
	if(custom.size()==0) printf("0.0\n");
	else printf("%.1f\n", totTime / 60.0 / custom.size());
	return 0;
}

1018 Public Bike Management(30)

Description
There is a public bike service in Hangzhou City which provides great convenience to the tourists from all over the world. One may rent a bike at any station and return it to any other stations in the city.
The Public Bike Management Center (PBMC) keeps monitoring the real-time capacity of all the stations. A station is said to be in perfect condition if it is exactly half-full. If a station is full or empty, PBMC will collect or send bikes to adjust the condition of that station to perfect. And more, all the stations on the way will be adjusted as well.
When a problem station is reported, PBMC will always choose the shortest path to reach that station. If there are more than one shortest path, the one that requires the least number of bikes sent from PBMC will be chosen.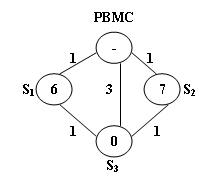

The above figure illustrates an example. The stations are represented by vertices and the roads correspond to the edges. The number on an edge is the time taken to reach one end station from another. The number written inside a vertex $S$ is the current number of bikes stored at $S$. Given that the maximum capacity of each station is 10. To solve the problem at $S_{3}$, we have 2 different shortest paths: PBMC -> $S_{1}$ -> $S_{3}$. In this case, 4 bikes must be sent from PBMC, because we can collect 1 bike from $S_{1}$ and then take 5 bikes to $S_{3}$, so that both stations will be in perfect conditions.
PBMC -> $S_{2}$ -> $S_{3}$. This path requires the same time as path 1, but only 3 bikes sent from PBMC and hence is the one that will be chosen.
Input Specification
Each input file contains one test case. For each case, the first line contains 4 numbers: $C_{max}$(≤100), always an even number, is the maximum capacity of each station; $N$ (≤500), the total number of stations; $S_{p}$, the index of the problem station (the stations are numbered from 1 to N, and PBMC is represented by the vertex 0); and $M$, the number of roads. The second line contains $N$ non-negative numbers $C_{i}$ (i=1,⋯,N) where each $C_{i}$ is the current number of bikes at Si respectively. Then $M$ lines follow, each contains 3 numbers: $S_{i}$, $S_{j}$, and $T_{​ij}$ which describe the time $T_{ij}$ taken to move betwen stations $_{i}$ and $S_{j}$. All the numbers in a line are separated by a space.
Output Specification
For each test case, print your results in one line. First output the number of bikes that PBMC must send. Then after one space, output the path in the format: 0−>$S_{1}$ −>⋯−>$S_{p}$. Finally after another space, output the number of bikes that we must take back to PBMC after the condition of $S{p}$ is adjusted to perfect.
Note that if such a path is not unique, output the one that requires minimum number of bikes that we must take back to PBMC. The judge’s data guarantee that such a path is unique.
Sample Input
10 3 3 5
6 7 0
0 1 1
0 2 1
0 3 3
1 3 1
2 3 1
Sample Output
3 0->2->3 0
Program

//有个测试点没过，气死我了！
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
#include<cmath>
using namespace std;
const int MAXV=502;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int dis;
	Node(){}
	Node(int V,int Dis):v(V),dis(Dis){}
};
vector<Node> Adj[MAXV];
bool vis[MAXV];
int dist[MAXV];
vector<int> pre[MAXV];
int weight[MAXV];
int need[MAXV];
int take[MAXV];
int N,C,S,M;
int minNeed=INF,minTake=INF;
struct Cmp{
	bool operator () (const int &a, const int &b) const{
		return dist[a]>dist[b];
	}
};

void Dijkstra(int s){
	priority_queue<int, vector<int>, Cmp> pq;
	pq.push(s);
	dist[s]=0;
	int nDone=0;
	while(nDone<N+1&&!pq.empty()){
		int u=pq.top();
		pq.pop();
		if(!vis[u]){
			vis[u]=true;
			nDone++;
			if(u==S) break;
		}else continue;
		for(int i=0;i<Adj[u].size();i++){
			int v=Adj[u][i].v;
			int dis=Adj[u][i].dis;
			if(!vis[v]){
				if(dist[u]+dis<dist[v]){
					dist[v]=dist[u]+dis;
					pre[v].clear();
					pre[v].push_back(u);
					pq.push(v);
				}else if(dist[u]+dis==dist[v]){
					pre[v].push_back(u);
				}
			}
		}
	}
}
vector<int> tmpPath, path;
void DFS(int u){
	if(u==0){
		vector<int> tmp;
		tmp=tmpPath;
		tmp.push_back(u);
		reverse(tmp.begin(), tmp.end());
		for(int i=1;i<tmp.size();i++){
			int u=tmp[i-1];
			int v=tmp[i];
			int tmpNeed=max(0, C/2-weight[v]);
			int tmpTake=max(0, weight[v]-C/2);
			need[v]=need[u]+max(0, tmpNeed-take[u]-tmpTake);
			take[v]=max(0, take[u]+tmpTake-tmpNeed);
		}

		if(need[S]<minNeed){
			minNeed=need[S];
			minTake=take[S];
			path=tmp;
		}else if(need[S]==minNeed){
			if(take[S]<minTake){
				minTake=take[S];
				path=tmp;
			}
		}
		return;
	}
	tmpPath.push_back(u);
	for(int i=0;i<pre[u].size();i++){
		DFS(pre[u][i]);
	}
	tmpPath.pop_back();
}
int main(){
	cin>>C>>N>>S>>M;
	memset(weight, 0, sizeof(weight));
	memset(dist, INF, sizeof(dist));
	memset(vis, false, sizeof(vis));
	memset(need, 0, sizeof(need));
	memset(take, 0, sizeof(take));
	for(int i=1;i<=N;i++){
		cin>>weight[i];
	}
	for(int i=0;i<M;i++){
		int u, v, dis;
		cin>>u>>v>>dis;
		Adj[u].push_back(Node(v, dis));
		Adj[v].push_back(Node(u, dis));
	}

	Dijkstra(0);
	DFS(S);

	cout<<minNeed<<" ";
	for(int i=0;i<path.size();i++){
		if(i!=0) cout<<"->";
		cout<<path[i];
	}
	cout<<" "<<minTake<<endl;
	return 0;
}

1019 General Palindromic Number(20)

Description
A number that will be the same when it is written forwards or backwards is known as a Palindromic Number. For example, 1234321 is a palindromic number. All single digit numbers are palindromic numbers.
Although palindromic numbers are most often considered in the decimal system, the concept of palindromicity can be applied to the natural numbers in any numeral system. Consider a number N>0 in base b≥2, where it is written in standard notation with k+1 digits ai as $\sum_{i=0}^k\left(a_ib^i\right)$. Here, as usual, 0≤ai<b for all i and ak is non-zero. Then N is palindromic if and only if $a_i=a_{k−i}$ for all i. Zero is written 0 in any base and is also palindromic by definition.
Given any positive decimal integer N and a base b, you are supposed to tell if N is a palindromic number in base b.
Input Specification
Each input file contains one test case. Each case consists of two positive numbers N and b, where $0<N≤10^9$is the decimal number and $2≤b≤10^9$is the base. The numbers are separated by a space.
Output Specification
For each test case, first print in one line Yes if N is a palindromic number in base b, or No if not. Then in the next line, print N as the number in base b in the form “$a_k,a_{k−1},…,a_0$”. Notice that there must be no extra space at the end of output.
Sample Input 1
27 2
Sample Output 1
Yes
1 1 0 1 1
Sample Input 2
121 5
Sample Output 2
No
4 4 1
Programs

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
int N, base;
vector<int> handle(int n, int base){
	vector<int> vec;
	while(n!=0){
		vec.push_back(n%base);
		n/=base;
	}
	return vec;
}
bool isPal(vector<int> vec){
	for(int i=0;i<vec.size()/2;i++){
		if(vec[i]!=vec[vec.size()-1-i]) return false;
	}
	return true;
}
int main(){
	cin>>N>>base;
	vector<int> vec=handle(N,base);
	reverse(vec.begin(),vec.end());
	if(isPal(vec)){
		cout<<"Yes"<<endl;
	}else cout<<"No"<<endl;
	for(int i=0;i<vec.size();i++){
		if(i!=0) cout<<" ";
		cout<<vec[i];
	}
	cout<<endl;
	return 0;
}

1020 Tree Traversals(25)

Description
Suppose that all the keys in a binary tree are distinct positive integers. Given the postorder and inorder traversal sequences, you are supposed to output the level order traversal sequence of the corresponding binary tree.
Input Specification
Each input file contains one test case. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the postorder sequence and the third line gives the inorder sequence. All the numbers in a line are separated by a space.
Output Specification
For each test case, print in one line the level order traversal sequence of the corresponding binary tree. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the end of the line.
Sample Input
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
Sample Output
4 1 6 3 5 7 2
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
struct Node{
	int data;
	Node *lchild, *rchild;
};
int N;
vector<int> inOrder, postOrder;
Node* create(int inL,int inR, int pL,int pR){
	if(inL>inR||pL>pR) return NULL;
	Node* root= new Node;
	root->data=postOrder[pR];
	int pos;
	for(pos=inL;pos<=inR;pos++){
		if(postOrder[pR]==inOrder[pos]) break;
	}
	int leftNum=pos-inL;
	root->lchild=create(inL,pos-1,pL,pL+leftNum-1);
	root->rchild=create(pos+1,inR,pL+leftNum, pR-1);
	return root;
}
void levelOrder(Node * root){
	if(root==NULL) return;
	queue<Node*> q;
	q.push(root);
	bool isFirst=true;
	while(!q.empty()){
		Node* now=q.front();
		if(isFirst) isFirst=false;
		else cout<<" ";
		cout<<now->data;
		q.pop();
		if(now->lchild!=NULL) q.push(now->lchild);
		if(now->rchild!=NULL) q.push(now->rchild);
	}
	cout<<endl;
}
int main(){
	cin>>N;
	inOrder.resize(N);
	postOrder.resize(N);
	for(int i=0;i<N;i++) cin>>postOrder[i];
	for(int i=0;i<N;i++) cin>>inOrder[i];
	levelOrder(create(0, N-1, 0, N-1));
	return 0;
}

1021 Deepest Root(25)

Description
A graph which is connected and acyclic can be considered a tree. The height of the tree depends on the selected root. Now you are supposed to find the root that results in a highest tree. Such a root is called the deepest root.
Input Specification
Each input file contains one test case. For each case, the first line contains a positive integer N ($≤10^{4}$) which is the number of nodes, and hence the nodes are numbered from 1 to N. Then N−1 lines follow, each describes an edge by given the two adjacent nodes’ numbers.
Output Specification
For each test case, print each of the deepest roots in a line. If such a root is not unique, print them in increasing order of their numbers. In case that the given graph is not a tree, print Error: K components where K is the number of connected components in the graph.
Sample Input 1
5
1 2
1 3
1 4
2 5
Sample Output 1
3
4
5
Sample Input 2
5
1 3
1 4
2 5
3 4
Sample Output 2
Error: 2 components
Program

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
#include<set>
using namespace std;
vector< vector<int> > vec;
int N;
vector<int> father;
vector<bool> vis;
int maxDepth=0;
vector<int> v[2];
int findFather(int x){
	if(x!=father[x]){
		father[x]=findFather(father[x]);
	}
	return father[x];
}
void unionSet(int a,int b){
	int fa=findFather(a);
	int fb=findFather(b);
	if(fa!=fb) father[fa]=fb;
}
void DFS(int vi, int i, int depth){
	vis[i]=true;
	if(depth>maxDepth){
		maxDepth=depth;
		v[vi].clear();
		v[vi].push_back(i);
	}else if(depth==maxDepth){
		v[vi].push_back(i);
	}
	for(int j=0;j<vec[i].size();j++){
		if(!vis[vec[i][j]]) DFS(vi, vec[i][j], depth+1);
	}
}
int main(){
	scanf("%d", &N);
	vec.resize(N+1);
	father.resize(N+1);
	vis.resize(N+1);
	for(int i=1;i<=N;i++){
		father[i]=i;
		vis[i]=false;
	}
	for(int i=0;i<N-1;i++){
		int a,b;
		scanf("%d%d",&a,&b);
		vec[a].push_back(b);
		vec[b].push_back(a);
		unionSet(a,b);
	}
	int component=0;
	for(int i=1;i<=N;i++){
		int fa=findFather(i);
		if(!vis[fa]){
			vis[fa]=true;
			component++;
		}
	}
	father.clear();
	if(component!=1){
		printf("Error: %d components\n", component);
	}else{
		fill(vis.begin(), vis.end(), false);
		DFS(0, 1, 0);

		fill(vis.begin(), vis.end(), false);
		DFS(1, v[0][0], 0);

		for(int i=0;i<v[1].size();i++) v[0].push_back(v[1][i]);

		sort(v[0].begin(), v[0].end());
		for(int i=0;i<v[0].size();i++){
			if(i==0) cout<<v[0][i]<<endl;
			else if(v[0][i]!=v[0][i-1]) cout<<v[0][i]<<endl;
		}
	}
	return 0;
}

1022 Digital Library(30)

Description
A Digital Library contains millions of books, stored according to their titles, authors, key words of their abstracts, publishers, and published years. Each book is assigned an unique 7-digit number as its ID. Given any query from a reader, you are supposed to output the resulting books, sorted in increasing order of their ID’s.
Input Specification
Each input file contains one test case. For each case, the first line contains a positive integer N (≤10​^4) which is the total number of books. Then N blocks follow, each contains the information of a book in 6 lines:
Line #1: the 7-digit ID number;
Line #2: the book title – a string of no more than 80 characters;
Line #3: the author – a string of no more than 80 characters;
Line #4: the key words – each word is a string of no more than 10 characters without any white space, and the keywords are separated by exactly one space;
Line #5: the publisher – a string of no more than 80 characters;
Line #6: the published year – a 4-digit number which is in the range [1000, 3000].
It is assumed that each book belongs to one author only, and contains no more than 5 key words; there are no more than 1000 distinct key words in total; and there are no more than 1000 distinct publishers.

After the book information, there is a line containing a positive integer M (≤1000) which is the number of user’s search queries. Then M lines follow, each in one of the formats shown below:
1: a book title
2: name of an author
3: a key word
4: name of a publisher
5: a 4-digit number representing the year
Output Specification
For each query, first print the original query in a line, then output the resulting book ID’s in increasing order, each occupying a line. If no book is found, print Not Found instead.

Sample Input
3
1111111
The Testing Book
Yue Chen
test code debug sort keywords
ZUCS Print
2011
3333333
Another Testing Book
Yue Chen
test code sort keywords
ZUCS Print2
2012
2222222
The Testing Book
CYLL
keywords debug book
ZUCS Print2
2011
6
1: The Testing Book
2: Yue Chen
3: keywords
4: ZUCS Print
5: 2011
3: blablabla
Sample Output
1: The Testing Book
1111111
2222222
2: Yue Chen
1111111
3333333
3: keywords
1111111
2222222
3333333
4: ZUCS Print
1111111
5: 2011
1111111
2222222
3: blablabla
Not Found
Program

#include<iostream>
#include<cstring>
#include<algorithm>
#include<map>
#include<set>
using namespace std;
map<string, set<string>> m[5];
int main(){
	int n;
	string str;
	cin>>n;
	for(int i=0;i<n;i++){
		string id;
		cin>>id;
		getchar();
		for(int j=0;j<5;j++){
			getline(cin, str);
			if(j!=2){
				m[j][str].insert(id);
			}else{
				while(str.find(' ')!=string::npos){
					int index=str.find(' ');
					string s1=str.substr(0, index);
					m[j][s1].insert(id);
					str=str.substr(index+1);
				}
				m[j][str].insert(id);
			}
		}
	}
	cin>>n;
	for(int i=0;i<n;i++){
		int q;
		cin>>q;
		getchar();
		getchar();
		getline(cin, str);
		cout<<q<<": "<<str<<endl;
		if(m[q-1].find(str)==m[q-1].end()) cout<<"Not Found"<<endl;
		else{
			for(set<string>::iterator it=m[q-1][str].begin();it!=m[q-1][str].end();it++){
				cout<<*it<<endl;
			}
		}
	}

	return 0;
}

1023 Have Fun with Numbers(20)

Description
Notice that the number 123456789 is a 9-digit number consisting exactly the numbers from 1 to 9, with no duplication. Double it we will obtain 246913578, which happens to be another 9-digit number consisting exactly the numbers from 1 to 9, only in a different permutation. Check to see the result if we double it again!
Now you are suppose to check if there are more numbers with this property. That is, double a given number with k digits, you are to tell if the resulting number consists of only a permutation of the digits in the original number.
Input Specification
Each input contains one test case. Each case contains one positive integer with no more than 20 digits.
Output Specification
For each test case, first print in a line “Yes” if doubling the input number gives a number that consists of only a permutation of the digits in the original number, or “No” if not. Then in the next line, print the doubled number.
Sample Input
1234567899
Sample Output
Yes
2469135798
Program

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
struct BigInteger{
	int b[1000];
	int len;
	BigInteger(){
		memset(b, 0, sizeof(b));
		len=0;
	}
	BigInteger(const string & str){
		len=str.length();
		memset(b, 0, sizeof(b));
		for(int i=0;i<len;i++){
			b[i]=str[len-1-i]-'0';
		}
	}
	void print(){
		for(int i=len-1;i>=0;i--){
			cout<<b[i];
		}
		cout<<endl;
	}
};
BigInteger mul(BigInteger big1,int b){
	BigInteger big;
	int carry=0;
	for(int i=0;i<big1.len;i++){
		int temp=big1.b[i]*b+carry;
		big.b[big.len++]=temp%10;
		carry=temp/10;
	}
	while(carry!=0){
		big.b[big.len++]=carry%10;
		carry/=10;
	}
	return big;
}

string str;
int m[10]={0};
int main(){
	cin>>str;
	BigInteger b(str);
	int sum=str.length();
	for(int i=0;i<str.length();i++){
		m[str[i]-'0']++;
	}
	BigInteger b2=mul(b, 2);
	for(int i=0;i<b2.len;i++){
		if(m[b2.b[i]]>0){
			m[b2.b[i]]--;
			sum--;
		}
		else{
			cout<<"No"<<endl;
			b2.print();
			return 0;
		}
	}
	if(sum==0){
		cout<<"Yes"<<endl;
	}else cout<<"No"<<endl;
	b2.print();
	return 0;
}

1024 Palindromic Number(25)

Description
A number that will be the same when it is written forwards or backwards is known as a Palindromic Number. For example, 1234321 is a palindromic number. All single digit numbers are palindromic numbers.
Non-palindromic numbers can be paired with palindromic ones via a series of operations. First, the non-palindromic number is reversed and the result is added to the original number. If the result is not a palindromic number, this is repeated until it gives a palindromic number. For example, if we start from 67, we can obtain a palindromic number in 2 steps: 67 + 76 = 143, and 143 + 341 = 484.
Given any positive integer N, you are supposed to find its paired palindromic number and the number of steps taken to find it.
Input Specification
Each input file contains one test case. Each case consists of two positive numbers N and K, where N ($≤10^{10}$) is the initial numer and K (≤100) is the maximum number of steps. The numbers are separated by a space.
Output Specification
For each test case, output two numbers, one in each line. The first number is the paired palindromic number of N, and the second number is the number of steps taken to find the palindromic number. If the palindromic number is not found after K steps, just output the number obtained at the Kth step and K instead.
Sample Input 1
67 3
Sample Output 1
484
2
Sample Input 2
69 3
Sample Output 2
1353
3
Program

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
struct BigInteger{
	int b[1000];
	int len;
	BigInteger(){
		memset(b, 0, sizeof(b));
		len=0;
	}
	BigInteger(const string &str){
		memset(b, 0, sizeof(b));
		len=str.length();
		for(int i=0;i<len;i++){
			b[i]=str[len-1-i]-'0';
		}
	}
	void print(){
		for(int i=len-1;i>=0;i--){
			cout<<b[i];
		}
		cout<<endl;
	}
};
BigInteger add(BigInteger b1, BigInteger b2){
	BigInteger big;
	int carry=0;
	for(int i=0;i<b1.len||i<b2.len;i++){
		int tmp=b1.b[i]+b2.b[i]+carry;
		big.b[big.len++]=tmp%10;
		carry=tmp/10;
	}
	if(carry!=0) big.b[big.len++]=carry;
	return big;
}
bool isPal(BigInteger big){
	for(int i=0;i<big.len/2;i++){
		if(big.b[i]!=big.b[big.len-1-i]) return false;
	}
	return true;
}
string str;
int k;
int main(){
	cin>>str>>k;
	BigInteger big(str);
	int step=0;
	while(!isPal(big)&&step<k){
		BigInteger tmp;
		for(int i=0;i<big.len;i++){
			tmp.b[i]=big.b[big.len-1-i];
		}
		tmp.len=big.len;
		big=add(tmp, big);
		step++;
	}
	big.print();
	cout<<step<<endl;
}

1025. PAT Ranking (25)

Programming Ability Test (PAT) is organized by the College of Computer Science and Technology of Zhejiang University. Each test is supposed to run simultaneously in several places, and the ranklists will be merged immediately after the test. Now it is your job to write a program to correctly merge all the ranklists and generate the final rank.
Input Specification
Each input file contains one test case. For each case, the first line contains a positive number N (<=100), the number of test locations. Then N ranklists follow, each starts with a line containing a positive integer K (<=300), the number of testees, and then K lines containing the registration number (a 13-digit number) and the total score of each testee. All the numbers in a line are separated by a space.
Output Specification
For each test case, first print in one line the total number of testees. Then print the final ranklist in the following format:
registration_number final_rank location_number local_rank
The locations are numbered from 1 to N. The output must be sorted in nondecreasing order of the final ranks. The testees with the same score must have the same rank, and the output must be sorted in nondecreasing order of their registration numbers.
Sample Input
2
5
1234567890001 95
1234567890005 100
1234567890003 95
1234567890002 77
1234567890004 85
4
1234567890013 65
1234567890011 25
1234567890014 100
1234567890012 85
Sample Output
9
1234567890005 1 1 1
1234567890014 1 2 1
1234567890001 3 1 2
1234567890003 3 1 2
1234567890004 5 1 4
1234567890012 5 2 2
1234567890002 7 1 5
1234567890013 8 2 3
1234567890011 9 2 4
Program

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
struct Student {
	long long id; //准考证号
	int score;  //分数
	int final_rank; //最终排名
	int location_number; //考场号
	int local_rank; //考场内排名
	Student(long long ID, int Score, int Final_rank,int Location_number, int Local_rank) {
		id = ID;
		score = Score;
		final_rank = Final_rank;
		location_number = Location_number;
		local_rank = Local_rank;
	}
	Student() {}
	bool operator < (const Student &temp) const
	{
		if (temp.score != score)
		{
			return score > temp.score;
		}
		return id < temp.id;
	}
}students[30010];
int main()
{
	int nLocation;
	int num = 0;
	cin >> nLocation;
	for (int i = 0; i < nLocation; i++)
	{
		int k;
		cin >> k;
		for (int j = 0; j < k; j++)
		{
			long long id, score;
			cin >> id >> score;
			students[num++] = Student(id, score,0, i+1, 0);
		}
		sort(students+num - k, students + num);
		students[num - k].local_rank = 1; //每个考场第一名排名记为1
		for (int j = num-k+1; j < num; j++)
		{
			if (students[j].score == students[j - 1].score)
			{
				students[j].local_rank = students[j - 1].local_rank;
			}
			else
			{
				students[j].local_rank = j +1- (num - k );
			}
		}
	}
	sort(students, students + num);
	cout << num << endl;
	//students[0].final_rank = 1;
	for (int i = 0; i < num; i++)
	{
		if (i>0&&students[i].score == students[i - 1].score)
		{
			students[i].final_rank = students[i - 1].final_rank;
		}
		else
		{
			students[i].final_rank = i+1;
		}
		printf("%013lld", students[i].id); //哦，以后还是用char好了！
		cout << " "/*<< students[i].score<<" "*/<<students[i].final_rank<<" "<<students[i].location_number << " " << students[i].local_rank << endl;
	}
	return 0;
}

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
using namespace std;
struct Student {
	char id[14]; //准考证号
	int score;  //分数
	int final_rank; //最终排名
	int location_number; //考场号
	int local_rank; //考场内排名
	Student(char* ID, int Score, int Final_rank,int Location_number, int Local_rank) {
		strcpy(id,ID);
		score = Score;
		final_rank = Final_rank;
		location_number = Location_number;
		local_rank = Local_rank;
	}
	Student() {}
	bool operator < (const Student &temp) const
	{
		if (temp.score != score)
		{
			return score > temp.score;
		}
		return strcmp(id,temp.id) < 0;
	}
}students[30010];
int main()
{
	int nLocation;
	int num = 0;
	cin >> nLocation;
	for (int i = 0; i < nLocation; i++)
	{
		int k;
		cin >> k;
		for (int j = 0; j < k; j++)
		{
			char id[14];
			int score;
			scanf("%s %d", id, &score);
			students[num++] = Student(id, score,0, i+1, 0);
		}
		sort(students+num - k, students + num);
		students[num - k].local_rank = 1; //每个考场第一名排名记为1
		for (int j = num-k+1; j < num; j++)
		{
			if (students[j].score == students[j - 1].score)
			{
				students[j].local_rank = students[j - 1].local_rank;
			}
			else
			{
				students[j].local_rank = j +1- (num - k );
			}
		}
	}
	sort(students, students + num);
	cout << num << endl;
	//students[0].final_rank = 1;
	for (int i = 0; i < num; i++)
	{
		if (i>0&&students[i].score == students[i - 1].score)
		{
			students[i].final_rank = students[i - 1].final_rank;
		}
		else
		{
			students[i].final_rank = i+1;
		}
		cout <<students[i].id<< " "/*<< students[i].score<<" "*/<<students[i].final_rank<<" "<<students[i].location_number << " " << students[i].local_rank << endl;
	}
	return 0;
}

1027 Colors in Mars(20)

Description
People in Mars represent the colors in their computers in a similar way as the Earth people. That is, a color is represented by a 6-digit number, where the first 2 digits are for Red, the middle 2 digits for Green, and the last 2 digits for Blue. The only difference is that they use radix 13 (0-9 and A-C) instead of 16. Now given a color in three decimal numbers (each between 0 and 168), you are supposed to output their Mars RGB values.
Input Specification
Each input file contains one test case which occupies a line containing the three decimal color values.
Output Specification
For each test case you should output the Mars RGB value in the following format: first output #, then followed by a 6-digit number where all the English characters must be upper-cased. If a single color is only 1-digit long, you must print a 0 to its left.
Sample Input
15 43 71
Sample Output
#123456
Program

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
const int BASE=13;
const char CH[]={'0','1','2','3','4','5','6','7','8','9','A','B','C'};
int a,b,c;
string transform(int x){
	int exp=0;
	string result="";
	while(x!=0){
		result+=CH[x%BASE];
		x/=BASE;
	}
	reverse(result.begin(),result.end());
	while(result.length()!=2) result="0"+result;
	return result;
}
int main(){
//	string ss="aaa";
//	printf(ss.c_str());
	cin>>a>>b>>c;
	cout<<"#"<<transform(a)<<transform(b)<<transform(c)<<endl;
	return 0;
}

1028 List Sorting(25)

Description
Excel can sort records according to any column. Now you are supposed to imitate this function.
Input Specification
Each input file contains one test case. For each case, the first line contains two integers $N$ $\left(≤10^5\right)$ and $C$, where $N$ is the number of records and $C$ is the column that you are supposed to sort the records with. Then N lines follow, each contains a record of a student. A student’s record consists of his or her distinct ID (a 6-digit number), name (a string with no more than 8 characters without space), and grade (an integer between 0 and 100, inclusive).
Output Specification
For each test case, output the sorting result in N lines. That is, if $C$ = 1 then the records must be sorted in increasing order according to ID’s; if $C$ = 2 then the records must be sorted in non-decreasing order according to names; and if $C$ = 3 then the records must be sorted in non-decreasing order according to grades. If there are several students who have the same name or grade, they must be sorted according to their ID’s in increasing order.
Sample Input 1
3 1
000007 James 85
000010 Amy 90
000001 Zoe 60
Sample Output 1
000001 Zoe 60
000007 James 85
000010 Amy 90
Sample Input 2
4 2
000007 James 85
000010 Amy 90
000001 Zoe 60
000002 James 98
Sample Output 2
000010 Amy 90
000002 James 98
000007 James 85
000001 Zoe 60
Sample Input 3
4 3
000007 James 85
000010 Amy 90
000001 Zoe 60
000002 James 90
Sample Output 3
000001 Zoe 60
000007 James 85
000002 James 90
000010 Amy 90
Program

#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
int n,c;
struct Node{
	int id;
	string name;
	int grade;
	Node(){}
	Node(int Id, string Name, int Grade):id(Id), name(Name), grade(Grade){}
	bool operator < (const Node &tmp) const{
		switch(c){
			case 1: return id < tmp.id;
			case 2:{
				if(name!=tmp.name) return name < tmp.name;
				else return id < tmp.id;
			}
			case 3:{
				if(grade!=tmp.grade) return grade < tmp.grade;
				else return id < tmp.id;
			}		
		}
	}
	void toString(){
		printf("%06d %s %d\n", id, name.c_str(), grade);
	}
};
vector<Node> vec;
int main(){
	cin>>n>>c;
	vec.resize(n);
	for(int i=0;i<n;i++){
		cin>>vec[i].id>>vec[i].name>>vec[i].grade;
	}
	sort(vec.begin(), vec.end());
	for(vector<Node>::iterator it=vec.begin();it!=vec.end();it++){
		it->toString();
	}
	return 0;
}

1029 Median(25)

Description
Given an increasing sequence S of N integers, the median is the number at the middle position. For example, the median of S1 = { 11, 12, 13, 14 } is 12, and the median of S2 = { 9, 10, 15, 16, 17 } is 15. The median of two sequences is defined to be the median of the nondecreasing sequence which contains all the elements of both sequences. For example, the median of S1 and S2 is 13.
Given two increasing sequences of integers, you are asked to find their median.
Input Specification
Each input file contains one test case. Each case occupies 2 lines, each gives the information of a sequence. For each sequence, the first positive integer N ($≤2×10^5$) is the size of that sequence. Then N integers follow, separated by a space. It is guaranteed that all the integers are in the range of long int.
Output Specification
For each test case you should output the median of the two given sequences in a line.
Sample Input
4 11 12 13 14
5 9 10 15 16 17
Sample Output
13
Program

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
vector<long> v1,v2;
int n,m;
int main(){
	cin>>n;
	v1.resize(n);
	for(int i=0;i<n;i++) scanf("%ld", &v1[i]);
	cin>>m;
	v2.resize(m);
	for(int i=0;i<m;i++) scanf("%ld", &v2[i]);
	int mid=(m+n-1)/2;
	int idx1,idx2;
	idx1=idx2=0;
	int index=0;
	while(idx1<n&&idx2<m){
		if(v1[idx1]<=v2[idx2]){
			if(index==mid){
				cout<<v1[idx1]<<endl;
				return 0;
			}
			index++;
			idx1++;
		}else{
			if(index==mid){
				cout<<v2[idx2]<<endl;
				return 0;
			}
			index++;
			idx2++;
		}
	}
	while(idx1<n){
		if(index==mid){
			cout<<v1[idx1]<<endl;
			return 0;
		}
		index++;
		idx1++;
	}
	while(idx2<m){
		if(index==mid){
			cout<<v2[idx2]<<endl;
			return 0;
		}
		index++;
		idx2++;
	}
	return 0;
}

1030 Travel Plan (30)

A traveler’s map gives the distances between cities along the highways, together with the cost of each highway. Now you are supposed to write a program to help a traveler to decide the shortest path between his/her starting city and the destination. If such a shortest path is not unique, you are supposed to output the one with the minimum cost, which is guaranteed to be unique.
Input Specification
Each input file contains one test case. Each case starts with a line containing 4 positive integers N, M, S, and D, where N (≤500) is the number of cities (and hence the cities are numbered from 0 to N−1); M is the number of highways; S and D are the starting and the destination cities, respectively. Then M lines follow, each provides the information of a highway, in the format:
City1 City2 Distance Cost
where the numbers are all integers no more than 500, and are separated by a space.
Output Specification
For each test case, print in one line the cities along the shortest path from the starting point to the destination, followed by the total distance and the total cost of the path. The numbers must be separated by a space and there must be no extra space at the end of output.
Sample Input
4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20
Sample Output
0 2 3 3 40
Program

//Dijkstra+堆
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int MAXV=501;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int dis;
	int cost;
	Node(){}
	Node(int vv,int dd,int cc):v(vv),dis(dd),cost(cc){}
	bool operator < (const Node& tmp) const{
		if(dis!=tmp.dis){
			return dis>tmp.dis;
		}else{
			return cost>tmp.cost;
		}
	}
};
vector<Node> Adj[MAXV];
int pre[MAXV];
int dist[MAXV];
bool bVis[MAXV];
int cost[MAXV];
int n,m,s,d;

void print(int v){
	if(v==s){
		cout<<s;
		return;
	}
	print(pre[v]);
	cout<<" "<<v;
}
void Dijkstra(int s){
	memset(dist,INF,sizeof(dist));
	memset(bVis,false,sizeof(bVis));
	memset(cost,INF,sizeof(cost));
	for(int i=0;i<n;i++) pre[i]=i;
	dist[s]=0;
	cost[s]=0;
	priority_queue<Node> pq;
	pq.push(Node(s,0,0));
	int nChecked=0;
	while(!pq.empty()&&nChecked<n){
		Node top=pq.top();
		pq.pop();
		bVis[top.v]=true;
		for(unsigned int i=0;i<Adj[top.v].size();i++){
			int v=Adj[top.v][i].v;
			int dis=Adj[top.v][i].dis;
			int cos=Adj[top.v][i].cost;
			if(!bVis[v]){
				if(dist[top.v]+dis<dist[v]){
					dist[v]=dist[top.v]+dis;
					pre[v]=top.v;
					cost[v]=cost[top.v]+cos;
					pq.push(Node(v,dist[v],cost[v]));
				}else if(dist[top.v]+dis==dist[v]){
					if(cost[top.v]+cos<cost[v]){
						pre[v]=top.v;
						cost[v]=cost[top.v]+cos;
						pq.push(Node(v,dist[v],cost[v]));
					}
				}
			}
		}
	}
}
int main(){
	cin>>n>>m>>s>>d;
	for(int i=0;i<m;i++){
		int u,v,dis,cos;
		cin>>u>>v>>dis>>cos;
		Adj[u].push_back(Node(v,dis,cos));
		Adj[v].push_back(Node(u,dis,cos));
	}
	Dijkstra(s);
	print(d);
	cout<<" "<<dist[d]<<" "<<cost[d]<<endl;
	return 0;
}

//Dijkstra+DFS
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int MAXV=501;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int dis;
	int cos;
	Node(){}
	Node(int vv,int dd,int cc):v(vv),dis(dd),cos(cc){}
	bool operator < (const Node& tmp) const{
		return dis>tmp.dis;

	}
};
vector<Node> Adj[MAXV];
vector<int> pre[MAXV];
int bVis[MAXV];
int dist[MAXV];
int optCost=INF;
int n,m,s,d;

vector<int> path,tmpPath;
int findUV(int u,int v){
	for(int i=0;i<Adj[u].size();i++){
		if(Adj[u][i].v==v){
			return Adj[u][i].cos;
		}
	}
	return 0;
}
void DFS(int v){
	if(v==s){
		tmpPath.push_back(v);
		int tmpCost=0;
		for(int i=tmpPath.size()-1;i>0;i--){
			int u=tmpPath[i],v=tmpPath[i-1];
			tmpCost+=findUV(u,v);
		}
		if(tmpCost<optCost){
			optCost=tmpCost;
			path=tmpPath;
		}
		tmpPath.pop_back();
		return;
	}
	tmpPath.push_back(v);
	for(int i=0;i<pre[v].size();i++){
		DFS(pre[v][i]);
	}
	tmpPath.pop_back();
}
void Dijkstra(int s){
	memset(bVis,false,sizeof(bVis));
	memset(dist,INF,sizeof(dist));
	dist[s]=0;
	priority_queue<Node> pq;
	pq.push(Node(s,0,0));
	int nChecked=0;
	while(!pq.empty()&&nChecked<n){
		Node top=pq.top();
		pq.pop();
		bVis[top.v]=true;
		for(int i=0;i<Adj[top.v].size();i++){
			int v=Adj[top.v][i].v;
			int dis=Adj[top.v][i].dis;
			if(!bVis[v]){
				if(dist[top.v]+dis<dist[v]){
					dist[v]=dist[top.v]+dis;
					pre[v].clear();
					pre[v].push_back(top.v);
					pq.push(Node(v,dist[v],0));
				}else if(dist[top.v]+dis==dist[v]){
					pre[v].push_back(top.v);
				}
			}
		}
	}
}
int main(){
	cin>>n>>m>>s>>d;
	for(int i=0;i<m;i++){
		int s,e,d,c;
		cin>>s>>e>>d>>c;
		Adj[s].push_back(Node(e,d,c));
		Adj[e].push_back(Node(s,d,c));
	}
	Dijkstra(s);
	DFS(d);
	for(int i=path.size()-1;i>=0;i--){
		cout<<path[i]<<" ";
	}
	cout<<dist[d]<<" "<<optCost<<endl;
	return 0;
}

1031 Hello World for U(20)

Description
Given any string of N (≥5) characters, you are asked to form the characters into the shape of U. For example, helloworld can be printed as:

h  d
e  l
l  r
lowo

That is, the characters must be printed in the original order, starting top-down from the left vertical line with n1characters, then left to right along the bottom line with n2 characters, and finally bottom-up along the vertical line with n3 characters. And more, we would like U to be as squared as possible – that is, it must be satisfied that $n_1=n_3=max\lbrace k | k\leq 2 for all 3\leq n_2\leq N\rbrace$ with $n_1+n_2+n_3−2=N$.
Input Specification
Each input file contains one test case. Each case contains one string with no less than 5 and no more than 80 characters in a line. The string contains no white space.
Output Specification
For each test case, print the input string in the shape of U as specified in the description.
Sample Input
helloworld!
Sample Output

h   !
e   d
l   l
lowor

Program

#include<iostream>
#include<cstring>
using namespace std;
string str;
int main(){
	cin>>str;
	int len=str.length();
	int l,r;
	l=r=(len+2)/3;
	int bottom=len-l-r;
	int start=0, end=len-1;
	for(int row=0;row<l;row++){
		cout<<str[start++];
		for(int i=0;i<bottom;i++){
			if(row!=l-1){
				cout<<" ";
			}else{
				cout<<str[start++];
			}
		}
		cout<<str[end--]<<endl;
	}
	return 0;
}

1032 Sharing(25)

Description
To store English words, one method is to use linked lists and store a word letter by letter. To save some space, we may let the words share the same sublist if they share the same suffix. For example, loading and being are stored as showed in Figure 1.
You are supposed to find the starting position of the common suffix (e.g. the position of i in Figure 1).
Input Specification
Each input file contains one test case. For each case, the first line contains two addresses of nodes and a positive N (≤10^5), where the two addresses are the addresses of the first nodes of the two words, and N is the total number of nodes. The address of a node is a 5-digit positive integer, and NULL is represented by −1.
Then N lines follow, each describes a node in the format:
Address Data Next
whereAddress is the position of the node, Data is the letter contained by this node which is an English letter chosen from { a-z, A-Z }, and Next is the position of the next node.
Output Specification
For each case, simply output the 5-digit starting position of the common suffix. If the two words have no common suffix, output -1 instead.
Sample Input 1
11111 22222 9
67890 i 00002
00010 a 12345
00003 g -1
12345 D 67890
00002 n 00003
22222 B 23456
11111 L 00001
23456 e 67890
00001 o 00010
Sample Output 1
67890
Sample Input 2
00001 00002 4
00001 a 10001
10001 s -1
00002 a 10002
10002 t -1
Sample Output 2
-1
Program

//呵呵，看了下网上答案，和书上标答，第一次找到的相同的就是答案了
//我从后往前找居然不对。。。？？搞笑
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
struct Node{
	int address;
	char data;
	int next;
	Node(){}
	Node(int Address, int Data, int Next):address(Address),data(Data),next(Next){}
};
vector<Node> vec;
vector<Node> order[2];
int add1, add2, n;
void fun(int start, int i){
	while(start!=-1){
		order[i].push_back(vec[start]);
		start=vec[start].next;
	}
}
int main(){
	cin>>add1>>add2>>n;
	vec.resize(100001);
	int add, next;
	char data;
	for(int i=0;i<n;i++){
		//scanf("%d %c %d", &add, &data, &next);
		cin>>add>>data>>next;
		vec[add]=Node(add,data,next);
	}
	fun(add1,0);
	fun(add2,1);
	reverse(order[0].begin(), order[0].end());
	reverse(order[1].begin(), order[1].end());
	int idx1, idx2;
	idx1=idx2=0;
	int start=-1;
	bool isGet=false;
	while(idx1<order[0].size()&&idx2<order[1].size()){
		if(order[0][idx1].data==order[1][idx2].data){
			idx1++;
			idx2++;
		}else{
			start=order[0][idx1].next;
			isGet=true;
			break;
		}
	}
	if(!isGet){
		if(idx1<order[0].size()) start=add2;
		else start=add1;
	}

	if(start!=-1) printf("%05d\n", start);
	else cout<<-1<<endl;
	return 0;
}

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
struct Node{
	char data;
	int next;
	bool flag;
	Node(){}
	Node(char Data, int Next, bool Flag):data(Data),next(Next),flag(Flag){}
};
vector<Node> vec;
int add1, add2, n;
int main(){
	cin>>add1>>add2>>n;
	vec.resize(100001);
	int add, next;
	char data;
	for(int i=0;i<n;i++){
		cin>>add>>data>>next;
		vec[add]=Node(data,next,false);
	}
	int p=-1;
	for(p=add1;p!=-1;p=vec[p].next){
		vec[p].flag=true;
	}
	for(p=add2;p!=-1;p=vec[p].next){
		if(vec[p].flag==true) break;
	}

	if(p!=-1) printf("%05d\n", p);
	else cout<<-1<<endl;
	return 0;
}

1033 To Fill or Not to Fill(25)

Description
With highways available, driving a car from Hangzhou to any other city is easy. But since the tank capacity of a car is limited, we have to find gas stations on the way from time to time. Different gas station may give different price. You are asked to carefully design the cheapest route to go.
Input Specification
Each input file contains one test case. For each case, the first line contains 4 positive numbers: Cmax(≤ 100), the maximum capacity of the tank; D (≤30000), the distance between Hangzhou and the destination city; Davg(≤20), the average distance per unit gas that the car can run; and N (≤ 500), the total number of gas stations. Then N lines follow, each contains a pair of non-negative numbers: Pi, the unit gas price, and Di(≤D), the distance between this station and Hangzhou, for i=1,⋯,N. All the numbers in a line are separated by a space.
Output Specification
For each test case, print the cheapest price in a line, accurate up to 2 decimal places. It is assumed that the tank is empty at the beginning. If it is impossible to reach the destination, print The maximum travel distance = X where X is the maximum possible distance the car can run, accurate up to 2 decimal places.
Sample Input 1
50 1300 12 8
6.00 1250
7.00 600
7.00 150
7.10 0
7.20 200
7.50 400
7.30 1000
6.85 300
Sample Output 1
749.17
Sample Input 2
50 1300 12 2
7.10 0
7.00 600
Sample Output 2
The maximum travel distance = 1200.00
Program

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
const int INF=0x3f3f3f3f;
double capacity;
double dstDis;
double avgDis;
int nStation;
double minPrice=0;
double maxDis=0;
struct Station{
	double price;
	double distance;
	bool operator < (const Station &tmp) const{
		return distance<tmp.distance;
	}
};
vector<Station> vec;
int main(){
	cin>>capacity>>dstDis>>avgDis>>nStation;
	vec.resize(nStation+1);
	for(int i=0;i<nStation;i++){
		cin>>vec[i].price>>vec[i].distance;
	}
	vec[nStation].price=0;
	vec[nStation].distance=dstDis;
	sort(vec.begin(),vec.end());

	if(vec[0].distance!=0){
		printf("The maximum travel distance = %.2lf\n",0);
		return 0;
	}
	int nowIndex=0;
	double nowCapacity=capacity;
	while(nowIndex<nStation){

		double tmpMinPrice=INF;
		int tmpMinIndex=nowIndex;
		for(int index=nowIndex+1;index<=nStation&&vec[index].distance<=vec[nowIndex].distance+capacity*avgDis;index++){
			if(vec[index].price<vec[nowIndex].price){
				tmpMinIndex=index;
				tmpMinPrice=vec[index].price;
				break;
			}
			if(tmpMinPrice>=vec[index].price){
				tmpMinPrice=vec[index].price;
				tmpMinIndex=index;
			}
		}
		if(tmpMinPrice==INF){
			printf("The maximum travel distance = %.2lf\n",vec[nowIndex].distance+capacity*avgDis);
			return 0;
		}
		if(vec[tmpMinIndex].price>=vec[nowIndex].price){
			minPrice+=nowCapacity*vec[nowIndex].price;
			nowCapacity=0;
		}else if((capacity-nowCapacity)*avgDis<vec[tmpMinIndex].distance-vec[nowIndex].distance){
			double tmpDis=vec[tmpMinIndex].distance-vec[nowIndex].distance;
			double arrivedDis=(capacity-nowCapacity)*avgDis;
			minPrice+=(tmpDis-arrivedDis)/avgDis*vec[nowIndex].price;
			nowCapacity-=(tmpDis-arrivedDis)/avgDis;
		}
		maxDis=vec[nowIndex].distance+capacity*avgDis;
		nowCapacity+=(vec[tmpMinIndex].distance-vec[nowIndex].distance)/avgDis;
		nowIndex=tmpMinIndex;
	}
	printf("%.2lf\n", minPrice);
	return 0;
}

1034 Head of a Gang(30)

Description
One way that the police finds the head of a gang is to check people’s phone calls. If there is a phone call between A and B, we say that A and B is related. The weight of a relation is defined to be the total time length of all the phone calls made between the two persons. A “Gang” is a cluster of more than 2 persons who are related to each other with total relation weight being greater than a given threthold K. In each gang, the one with maximum total weight is the head. Now given a list of phone calls, you are supposed to find the gangs and the heads.
Input Specification
Each input file contains one test case. For each case, the first line contains two positive numbers N and K (both less than or equal to 1000), the number of phone calls and the weight threthold, respectively. Then N lines follow, each in the following format:
Name1 Name2 Time
where Name1 and Name2 are the names of people at the two ends of the call, and Time is the length of the call. A name is a string of three capital letters chosen from A-Z. A time length is a positive integer which is no more than 1000 minutes.
Output Specification
For each test case, first print in a line the total number of gangs. Then for each gang, print in a line the name of the head and the total number of the members. It is guaranteed that the head is unique for each gang. The output must be sorted according to the alphabetical order of the names of the heads.
Sample Input 1
8 59
AAA BBB 10
BBB AAA 20
AAA CCC 40
DDD EEE 5
EEE DDD 70
FFF GGG 30
GGG HHH 20
HHH FFF 10
Sample Output 1
2
AAA 3
GGG 3
Sample Input 2
8 70
AAA BBB 10
BBB AAA 20
AAA CCC 40
DDD EEE 5
EEE DDD 70
FFF GGG 30
GGG HHH 20
HHH FFF 10
Sample Output 2
0
Program

//图DFS！
#include<iostream>
#include<map>
#include<cstring>
using namespace std;

const int MAXV=2001;
const int INF=0x3f3f3f3f;

int G[MAXV][MAXV];
bool vis[MAXV];
int weight[MAXV];

map<string,int> stringToInt;//姓名->编号
map<int,string> intToString;//编号->姓名
map<string,int> gangs;//Head，人数
int numPersons;
int N,K;
void DFS(int u,int &head,int &totalWeight,int &members){
	vis[u]=true;
	members++;
	if(weight[u]>weight[head]){
		head=u;
	}
	for(int v=0;v<numPersons;v++){
//ERROR:注意环！如果先判断vis则导致有边权未统计
//		if(!vis[v]&&G[u][v]!=0){
//			totalWeight+=G[u][v];
//			DFS(v,head,totalWeight,members);
//		}
		if(G[u][v]!=0){
			totalWeight+=G[u][v];
			G[u][v]=G[v][u]=0;
			if(!vis[v]){
				DFS(v,head,totalWeight,members);
			}
		}
	}
}
void DFSTraverse(){
	for(int u=0;u<numPersons;u++){
		if(!vis[u]){
			int head=u;
			int totalWeight=0;
			int members=0;
			DFS(u,head,totalWeight,members);
			if(members>2&&totalWeight>K){
				gangs[intToString[head]]=members;
			}
		}
	}
}
//获取编号
int getNumber(string str){
	if(stringToInt.find(str)!=stringToInt.end()){
		return stringToInt[str];
	}else{
		stringToInt[str]=numPersons;
		intToString[numPersons]=str;
		return numPersons++;
	}
}
int main(){
	while(cin>>N>>K){
		//初始化
		numPersons=0;
		gangs.clear();
		intToString.clear();
		stringToInt.clear();
		memset(vis,false,sizeof(vis));
		memset(weight,0,sizeof(weight));
		memset(G,0,sizeof(G));
		//输入
		string name1,name2;
		int w;
		for(int i=0;i<N;i++){
			cin>>name1>>name2>>w;
			int num1=getNumber(name1);
			int num2=getNumber(name2);
			weight[num1]+=w;
			weight[num2]+=w;
			G[num1][num2]+=w; //重复边
			G[num2][num1]+=w;
		}
		//运算
		DFSTraverse();
		//输出
		cout<<gangs.size()<<endl;
		for(map<string,int>::iterator it=gangs.begin();it!=gangs.end();it++){
			cout<<it->first<<" "<<it->second<<endl;
		}
	}
	return 0;
}

//并查集
#include<iostream>
#include<cstring>
#include<map>
#include<set>
using namespace std;

const int MAXV=2001;
int weight[MAXV];
int N,K;
map<string,int> stringToInt;//姓名-编号
map<int,string> intToString;//编号-姓名
map<string,int> gangs;
struct Node{
	int father;
	int head;
	int count;
	int totalWeight;
};
Node nodes[MAXV];
int numPersons;
void makeSet(){
	numPersons=0;
	stringToInt.clear();
	intToString.clear();
	gangs.clear();
	memset(weight,0,sizeof(weight));

	for(int i=0;i<MAXV;i++){
		nodes[i].father=i;
		nodes[i].head=i;
		nodes[i].count=1;
		nodes[i].totalWeight=weight[i];
	}
}
int findFather(int i){
	if(i!=nodes[i].father){
		nodes[i].father=findFather(nodes[i].father);
	}
	return nodes[i].father;
}
void unionSet(int i,int j,int w){
	int fa=findFather(i);
	int fb=findFather(j);
	if(fa!=fb){
		nodes[fa].father=fb;
		nodes[fb].totalWeight+=w+nodes[fa].totalWeight;
		nodes[fb].count+=nodes[fa].count;

		//每次更新，head会在原有两个结合中的 head以及两个端点中选择 ，下同
		nodes[fb].head=(weight[nodes[fa].head]>weight[nodes[fb].head])?nodes[fa].head:nodes[fb].head;

		int wI=weight[i];
		int wJ=weight[j];
		if(wI>weight[nodes[fb].head]) nodes[fb].head=i;
		if(wJ>weight[nodes[fb].head]) nodes[fb].head=j;

//		cout<<"fb->head:"<<nodes[fb].head<<":"<<intToString[nodes[fb].head]<<" weight:"<<weight[nodes[fb].head]<<endl;
//		system("pause");
	}else{
		nodes[fa].totalWeight+=w;

		int wI=weight[i];
		int wJ=weight[j];
		if(wI>weight[nodes[fa].head]) nodes[fa].head=i;
		if(wJ>weight[nodes[fa].head]) nodes[fa].head=j;
//		cout<<"fa>head:"<<nodes[fa].head<<":"<<intToString[nodes[fa].head]<<" weight:"<<weight[nodes[fa].head]<<endl;
//		system("pause");
	}
}
int getNumber(string str){
	if(stringToInt.find(str)!=stringToInt.end()){
		return stringToInt[str];
	}else{
		stringToInt[str]=numPersons;
		intToString[numPersons]=str;
		return numPersons++;
	}
}
int main(){
	while(cin>>N>>K){
		makeSet();
		for(int i=0;i<N;i++){
			string name1,name2;
			int w;
			cin>>name1>>name2>>w;
			int num1=getNumber(name1);
			int num2=getNumber(name2);
			weight[num1]+=w;
			weight[num2]+=w;
			unionSet(num1,num2,w);
		}
		set<int> s;
		for(int i=0;i<numPersons;i++){
			int f=findFather(i);
			if(s.count(f)==0){
				s.insert(f);
			}
		}
		for(set<int>::iterator it=s.begin();it!=s.end();it++){
			int head=nodes[*it].head;
			if(nodes[*it].count>2&&nodes[*it].totalWeight>K){
				gangs[intToString[head]]=nodes[*it].count;
			}
		}

		cout<<gangs.size()<<endl;
		for(map<string,int>::iterator it=gangs.begin();it!=gangs.end();it++){
			cout<<it->first<<" "<<it->second<<endl;
		}
	}
	return 0;
}

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<map>
#include<set>
using namespace std;
int N,K;
struct Node{
	int father;
	int count;
	int weight;
	int head;
	int totalWeight;
};
vector<Node> node;
int person=0;
int findFather(int x){
	if(x!=node[x].father){
		node[x].father=findFather(node[x].father);
	}
	return node[x].father;
}
void unionSet(int a, int b, int w){
	int fa=findFather(a);
	int fb=findFather(b);
	node[a].weight+=w;
	node[b].weight+=w;
	if(fa!=fb){
		node[fa].father=fb;
		node[fb].count+=node[fa].count;
		node[fb].totalWeight+=node[fa].totalWeight+w;


		node[fb].head=(node[node[fa].head].weight>node[node[fb].head].weight)?node[fa].head:node[fb].head;

		if(node[a].weight>node[node[fb].head].weight) node[fb].head=a;
		if(node[b].weight>node[node[fb].head].weight) node[fb].head=b;
	}else{
		node[fb].totalWeight+=w;

		if(node[a].weight>node[node[fb].head].weight) node[fb].head=a;
		if(node[b].weight>node[node[fb].head].weight) node[fb].head=b;
	}
}
map<string, int> sToi;
map<int, string> iTos;
int getInt(string str){
	if(sToi.find(str)==sToi.end()){
		sToi[str]=person;
		iTos[person++]=str;
	}
	return sToi[str];
}
int main(){
	cin>>N>>K;
	node.resize(2*N);
	for(int i=0;i<2*N;i++){
		node[i].father=i;
		node[i].count=1;
		node[i].weight=0;
		node[i].totalWeight=0;
		node[i].head=i;
	}
	for(int i=0;i<N;i++){
		string str1, str2;
		int x;
		cin>>str1>>str2>>x;
		int idx1=getInt(str1);
		int idx2=getInt(str2);
		unionSet(idx1,idx2,x);
	}

	vector<bool> vis;
	vis.resize(person);
	fill(vis.begin(), vis.end(), false);
	set<string> result;
	for(int i=0;i<person;i++){
		int fa=findFather(i);
		if(!vis[fa]){
			vis[fa]=true;
			if(node[fa].count>2&&node[fa].totalWeight>K) result.insert(iTos[node[fa].head]);
		}
	}
	cout<<result.size()<<endl;
	for(set<string>::iterator it=result.begin();it!=result.end();it++){
		cout<<*it<<" "<<node[findFather(sToi[*it])].count<<endl;
	}
	return 0;
}

1035 Password(20)

Description
To prepare for PAT, the judge sometimes has to generate random passwords for the users. The problem is that there are always some confusing passwords since it is hard to distinguish 1 (one) from l (L in lowercase), or 0 (zero) from O (o in uppercase). One solution is to replace 1 (one) by @, 0 (zero) by %, l by L, and O by o. Now it is your job to write a program to check the accounts generated by the judge, and to help the juge modify the confusing passwords.
Input Specification
Each input file contains one test case. Each case contains a positive integer N (≤1000), followed by N lines of accounts. Each account consists of a user name and a password, both are strings of no more than 10 characters with no space.
Output Specification
For each test case, first print the number M of accounts that have been modified, then print in the following M lines the modified accounts info, that is, the user names and the corresponding modified passwords. The accounts must be printed in the same order as they are read in. If no account is modified, print in one line There are N accounts and no account is modified where N is the total number of accounts. However, if N is one, you must print There is 1 account and no account is modified instead.
Sample Input 1
3
Team000002 Rlsp0dfa
Team000003 perfectpwd
Team000001 R1spOdfa
Sample Output 1
2
Team000002 RLsp%dfa
Team000001 R@spodfa
Sample Input 2
1
team110 abcdefg332
Sample Output 2
There is 1 account and no account is modified
Sample Input 3
2
team110 abcdefg222
team220 abcdefg333
Sample Output 3
There are 2 accounts and no account is modified
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<map>
#include<vector>
using namespace std;
int N;
map<char, char> m;
string name, passward;
struct Node{
	string name, passward;
	Node(){}
	Node(string nn, string pp):name(nn), passward(pp){}
};
vector<Node> vec;
int main(){
	m['1']='@';
	m['0']='%';
	m['l']='L';
	m['O']='o';
	cin>>N;
	for(int i=0;i<N;i++){
		cin>>name>>passward;
		bool isModified=false;
		for(int j=0;j<passward.length();j++){
			if(passward[j]=='1'||passward[j]=='l'||
			   passward[j]=='0'||passward[j]=='O'){
				passward[j]=m[passward[j]];
				isModified=true;
			}
		}
		if(isModified) vec.push_back(Node(name,passward));
	}
	if(vec.size()!=0){
		cout<<vec.size()<<endl;
		for(int i=0;i<vec.size();i++){
			cout<<vec[i].name<<" "<<vec[i].passward<<endl;
		}
	}else{
		cout<<"There ";

		if(N>1)cout<<"are";
		else cout<<"is";

		cout<<" "<<N<<" account";
		if(N>1) cout<<"s";
		cout<<" and no account is modified"<<endl;
	}
	return 0;
}

1036 Boys vs Girls(25)

Description
This time you are asked to tell the difference between the lowest grade of all the male students and the highest grade of all the female students.
Input Specification
Each input file contains one test case. Each case contains a positive integer N, followed by N lines of student information. Each line contains a student’s name, gender, ID and grade, separated by a space, where name and ID are strings of no more than 10 characters with no space, gender is either F (female) or M (male), and grade is an integer between 0 and 100. It is guaranteed that all the grades are distinct.
Output Specification
For each test case, output in 3 lines. The first line gives the name and ID of the female student with the highest grade, and the second line gives that of the male student with the lowest grade. The third line gives the difference $grade_​F$−$grade_M$. If one such kind of student is missing, output Absent in the corresponding line, and output NA in the third line instead.
Sample Input 1
3
Joe M Math990112 89
Mike M CS991301 100
Mary F EE990830 95
Sample Output 1
Mary EE990830
Joe Math990112
6
Sample Input 2
1
Jean M AA980920 60
Sample Output 2
Absent
Jean AA980920
NA
Program

#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
struct Node{
	string name, id;
	char gender;
	int score;
	Node(){}
	Node(string nn, char g, string Id, int s):name(nn),id(Id),gender(g),score(s){}
	bool operator < (const Node &tmp) const{
		if(gender=='M'){
			return score < tmp.score;
		}else{
			return score > tmp.score;
		}
	}
};
int main(){
	int n;
	cin>>n;
	vector<Node> male, female;
	for(int i=0;i<n;i++){
		string name, id;
		char gender;
		int score;
		cin>>name>>gender>>id>>score;
		if(gender=='M'){
			male.push_back(Node(name, gender, id, score));
		}else{
			female.push_back(Node(name,gender, id, score));
		}
	}
	sort(male.begin(), male.end());
	sort(female.begin(), female.end());
	bool isAbsent=false;
	if(female.size()==0){
		isAbsent=true;
		cout<<"Absent"<<endl;
	}else{
		cout<<female[0].name<<" "<<female[0].id<<endl;
	}
	if(male.size()==0){
		isAbsent=true;
		cout<<"Absent"<<endl;
	}else{
		cout<<male[0].name<<" "<<male[0].id<<endl;
	}
	if(!isAbsent){
		cout<<female[0].score-male[0].score<<endl;
	}else{
		cout<<"NA"<<endl;
	}
	return 0;
}

1037 Magic Coupon(25)

Description
The magic shop in Mars is offering some magic coupons. Each coupon has an integer N printed on it, meaning that when you use this coupon with a product, you may get N times the value of that product back! What is more, the shop also offers some bonus product for free. However, if you apply a coupon with a positive N to this bonus product, you will have to pay the shop N times the value of the bonus product… but hey, magically, they have some coupons with negative N’s!
For example, given a set of coupons { 1 2 4 −1 }, and a set of product values { 7 6 −2 −3 } (in Mars dollars M$) where a negative value corresponds to a bonus product. You can apply coupon 3 (with N being 4) to product 1 (with value M$7) to get M$28 back; coupon 2 to product 2 to get M$12 back; and coupon 4 to product 4 to get M$3 back. On the other hand, if you apply coupon 3 to product 4, you will have to pay M$12 to the shop.
Each coupon and each product may be selected at most once. Your task is to get as much money back as possible.
Input Specification
Each input file contains one test case. For each case, the first line contains the number of coupons $N_C$, followed by a line with NCcoupon integers. Then the next line contains the number of products NP, followed by a line with N​P product values. Here $1≤N_C,N_P≤10^5$, and it is guaranteed that all the numbers will not exceed 230.
Output Specification
For each test case, simply print in a line the maximum amount of money you can get back.
Sample Input
4
1 2 4 -1
4
7 6 -2 -3
Sample Output
43
Program

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
vector<int> coupons, products;
int n, m;
int main(){
	cin>>n;
	coupons.resize(n);
	for(int i=0;i<n;i++) cin>>coupons[i];
	cin>>m;
	products.resize(m);
	for(int i=0;i<m;i++) cin>>products[i];
	sort(coupons.begin(),coupons.end());
	sort(products.begin(), products.end());
	int idx=0;
	int maxSum=0;
	while(idx<n&&idx<m&&coupons[idx]<0&&products[idx]<0){
		maxSum+=coupons[idx]*products[idx];
		idx++;
	}
	int idxC=n-1, idxP=m-1;
	while(idxC>=0&&idxP>=0&&coupons[idxC]>0&&products[idxP]>0){
		maxSum+=coupons[idxC]*products[idxP];
		idxC--;
		idxP--;
	}
	cout<<maxSum<<endl;
	return 0;
}

1038 Recover the Smallest Number(30)

Description
Given a collection of number segments, you are supposed to recover the smallest number from them. For example, given { 32, 321, 3214, 0229, 87 }, we can recover many numbers such like 32-321-3214-0229-87 or 0229-32-87-321-3214 with respect to different orders of combinations of these segments, and the smallest number is 0229-321-3214-32-87.
Input Specification
Each input file contains one test case. Each case gives a positive integer N ($≤10^4$) followed by N number segments. Each segment contains a non-negative integer of no more than 8 digits. All the numbers in a line are separated by a space.
Output Specification
For each test case, print the smallest number in one line. Notice that the first digit must not be zero.
Sample Input
5 32 321 3214 0229 87
Sample Output
22932132143287
Program

#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
bool cmp(string a, string b){
	return a+b<b+a;
}
int n;
vector<string> vec;
int main(){
	cin>>n;
	vec.resize(n);
	for(int i=0;i<n;i++)cin>>vec[i];
	sort(vec.begin(), vec.end(), cmp);
	string result;
	for(int i=0;i<n;i++) result+=vec[i];
	while(result.length()>0&&result[0]=='0'){
		result.erase(result.begin());
	}
	if(result.length()==0) cout<<0<<endl;
	else cout<<result<<endl;
	return 0;
}

1039 Course List for Student(25)

Description
Zhejiang University has 40000 students and provides 2500 courses. Now given the student name lists of all the courses, you are supposed to output the registered course list for each student who comes for a query.
Input Specification
Each input file contains one test case. For each case, the first line contains 2 positive integers: N (≤40,000), the number of students who look for their course lists, and K (≤2,500), the total number of courses. Then the student name lists are given for the courses (numbered from 1 to K) in the following format: for each course i, first the course index i and the number of registered students Ni(≤200) are given in a line. Then in the next line, Ni student names are given. A student name consists of 3 capital English letters plus a one-digit number. Finally the last line contains the N names of students who come for a query. All the names and numbers in a line are separated by a space.
Output Specification
For each test case, print your results in N lines. Each line corresponds to one student, in the following format: first print the student’s name, then the total number of registered courses of that student, and finally the indices of the courses in increasing order. The query results must be printed in the same order as input. All the data in a line must be separated by a space, with no extra space at the end of the line.
Sample Input
11 5
4 7
BOB5 DON2 FRA8 JAY9 KAT3 LOR6 ZOE1
1 4
ANN0 BOB5 JAY9 LOR6
2 7
ANN0 BOB5 FRA8 JAY9 JOE4 KAT3 LOR6
3 1
BOB5
5 9
AMY7 ANN0 BOB5 DON2 FRA8 JAY9 KAT3 LOR6 ZOE1
ZOE1 ANN0 BOB5 JOE4 JAY9 FRA8 DON2 AMY7 KAT3 LOR6 NON9
Sample Output
ZOE1 2 4 5
ANN0 3 1 2 5
BOB5 5 1 2 3 4 5
JOE4 1 2
JAY9 4 1 2 4 5
FRA8 3 2 4 5
DON2 2 4 5
AMY7 1 5
KAT3 3 2 4 5
LOR6 4 1 2 4 5
NON9 0
Program

//最后一个测试点超时了o(╥﹏╥)o
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<map>
using namespace std;
int n, k;
map<string, vector<int> > m;
int main(){
	cin>>n>>k;
	for(int i=0;i<k;i++){
		int course, count;
		cin>>course>>count;
		for(int j=0;j<count;j++){
			string name;
			cin>>name;
			vector<int> vec;
			if(m.find(name)==m.end()) m[name]=vec;
			m[name].push_back(course);
		}
	}
	for(int i=0;i<n;i++){
		string name;
		cin>>name;
		if(m.find(name)==m.end()) cout<<name<<" 0"<<endl;
		else{
			cout<<name<<" "<<m[name].size();
			sort(m[name].begin(),m[name].end());
			for(int i=0;i<m[name].size();i++) cout<<" "<<m[name][i];
			cout<<endl;
		}
	}
	return 0;
}

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<map>
using namespace std;
const int MAXN=26*26*26*10+1;
int n, k;
vector<int> courses[MAXN];
int change(string name){
	int result=0;
	for(int i=0;i<3;i++){
		result=result*26+name[i]-'A';
	}
	result=result*10+name[3]-'0';
	return result;
}
int main(){
	cin>>n>>k;
	for(int i=0;i<k;i++){
		int course, count;
		cin>>course>>count;
		for(int j=0;j<count;j++){
			string name;
			cin>>name;
			courses[change(name)].push_back(course);
		}
	}
	for(int i=0;i<n;i++){
		string name;
		cin>>name;
		cout<<name<<" "<<courses[change(name)].size();
		sort(courses[change(name)].begin(),courses[change(name)].end());
		for(int j=0;j<courses[change(name)].size();j++){
			cout<<" "<<courses[change(name)][j];
		}
		cout<<endl;
	}
	return 0;
}

1040 Longest Symmetric String(25)

Description
Given a string, you are supposed to output the length of the longest symmetric sub-string. For example, given Is PAT&TAP symmetric?, the longest symmetric sub-string is s PAT&TAP s, hence you must output 11.
Input Specification
Each input file contains one test case which gives a non-empty string of length no more than 1000.
Output Specification
For each test case, simply print the maximum length in a line.
Sample Input
Is PAT&TAP symmetric?
Sample Output
11
Program

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
string str;
int dp[1001][1001];
int main(){
	getline(cin, str);
	memset(dp, 0,sizeof(dp));
	int maxL=1;
	for(int i=0;i<str.length();i++){
		dp[i][i]=1;
		if(i<str.length()-1){
			if(str[i]==str[i+1]){
				dp[i][i+1]=1;
				maxL=2;
			}
		}
	}

	for(int L=3;L<=str.length();L++){
		for(int i=0;i+L-1<str.length();i++){
			int j=i+L-1;
			if(str[i]==str[j]){
				dp[i][j]=dp[i+1][j-1];
				if(dp[i][j]==1) maxL=L;
			}
		}
	}
	cout<<maxL<<endl;
	return 0;
}

1041 Be Unique(20)

Description
Being unique is so important to people on Mars that even their lottery is designed in a unique way. The rule of winning is simple: one bets on a number chosen from $[1,10^4]$. The first one who bets on a unique number wins. For example, if there are 7 people betting on { 5 31 5 88 67 88 17 }, then the second one who bets on 31 wins.
Input Specification
Each input file contains one test case. Each case contains a line which begins with a positive integer N ($≤10^5$) and then followed by N bets. The numbers are separated by a space.
Output Specification
For each test case, print the winning number in a line. If there is no winner, print None instead.
Sample Input 1
7 5 31 5 88 67 88 17
Sample Output 1
31
Sample Input 2
5 888 666 666 888 888
Sample Output 2
None
Program

#include<iostream>
#include<vector>
using namespace std;
int hashT[10001]={0};
int n;
vector<int> vec;
int main(){
	cin>>n;
	vec.resize(n);
	for(int i=0;i<n;i++){
		cin>>vec[i];
		hashT[vec[i]]++;
	}
	bool isPrint=false;
	for(int i=0;i<n;i++){
		if(hashT[vec[i]]==1){
			cout<<vec[i]<<endl;
			isPrint=true;
			break;
		}
	}
	if(!isPrint) cout<<"None"<<endl;
	return 0;
}

1042 Shuffling Machine(20)

Description
Shuffling is a Program used to randomize a deck of playing cards. Because standard shuffling techniques are seen as weak, and in order to avoid “inside jobs” where employees collaborate with gamblers by performing inadequate shuffles, many casinos employ automatic shuffling machines. Your task is to simulate a shuffling machine.

The machine shuffles a deck of 54 cards according to a given random order and repeats for a given number of times. It is assumed that the initial status of a card deck is in the following order:

S1, S2, …, S13,
H1, H2, …, H13,
C1, C2, …, C13,
D1, D2, …, D13,
J1, J2
where “S” stands for “Spade”, “H” for “Heart”, “C” for “Club”, “D” for “Diamond”, and “J” for “Joker”. A given order is a permutation of distinct integers in [1, 54]. If the number at the i-th position is j, it means to move the card from position i to position j. For example, suppose we only have 5 cards: S3, H5, C1, D13 and J2. Given a shuffling order {4, 2, 5, 3, 1}, the result will be: J2, H5, D13, S3, C1. If we are to repeat the shuffling again, the result will be: C1, H5, S3, J2, D13.

Input Specification
Each input file contains one test case. For each case, the first line contains a positive integer K (≤20) which is the number of repeat times. Then the next line contains the given order. All the numbers in a line are separated by a space.

Output Specification
For each test case, print the shuffling results in one line. All the cards are separated by a space, and there must be no extra space at the end of the line.

Sample Input
2
36 52 37 38 3 39 40 53 54 41 11 12 13 42 43 44 2 4 23 24 25 26 27 6 7 8 48 49 50 51 9 10 14 15 16 5 17 18 19 1 20 21 22 28 29 30 31 32 33 34 35 45 46 47
Sample Output
S7 C11 C10 C12 S1 H7 H8 H9 D8 D9 S11 S12 S13 D10 D11 D12 S3 S4 S6 S10 H1 H2 C13 D2 D3 D4 H6 H3 D13 J1 J2 C1 C2 C3 C4 D1 S5 H5 H11 H12 C6 C7 C8 C9 S2 S8 S9 H10 D5 D6 D7 H4 H13 C5
Programs

#include<iostream>
using namespace std;
const int N=54;
int s[N+1], e[N+1], loc[N+1];
int K;
char mp[5] = {'S', 'H', 'C', 'D', 'J'};

int main(){
	cin>>K;
	for(int i=1;i<=N;i++){
		s[i]=i;
	}
	for(int i=1;i<=N;i++){
		cin>>loc[i];
	}
	for(int step=0;step<K;step++){
		for(int i=1;i<=N;i++){
			e[loc[i]]=s[i];
		}
		for(int i=0;i<=N;i++){
			s[i]=e[i];
		}
	}
	for(int i=1;i<=N;i++){
		if(i!=1) cout<<" ";
		int index=(s[i]-1)/13;
		int num=(s[i]-1)%13+1;
		cout<<mp[index]<<num;
	}
	cout<<endl;
	return 0;
}

1043 Is It a Binary Search Tree(25)

Description
A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

• The left subtree of a node contains only nodes with keys less than the node’s key.
• The right subtree of a node contains only nodes with keys greater than or equal to the node’s key.
• Both the left and right subtrees must also be binary search trees.
  If we swap the left and right subtrees of every node, then the resulting tree is called the Mirror Image of a BST.
  Now given a sequence of integer keys, you are supposed to tell if it is the preorder traversal sequence of a BST or the mirror image of a BST.

Input Specification
Each input file contains one test case. For each case, the first line contains a positive integer N (≤1000). Then N integer keys are given in the next line. All the numbers in a line are separated by a space.
Output Specification
For each test case, first print in a line YES if the sequence is the preorder traversal sequence of a BST or the mirror image of a BST, or NO if not. Then if the answer is YES, print in the next line the postorder traversal sequence of that tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line.
Sample Input 1
7
8 6 5 7 10 8 11
Sample Output 1
YES
5 7 6 8 11 10 8
Sample Input 2
7
8 10 11 8 6 7 5
Sample Output 2
YES
11 8 10 7 5 6 8
Sample Input 3
7
8 6 8 5 10 9 11
Sample Output 3
NO
Program

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
struct Node{
	int data;
	Node* lchild;
	Node* rchild;
};
vector<int> origin,pre,preMirror,post,postMirror;
int n;
void insert(Node* &root,int x){
	if(root==NULL){
		root=new Node;
		root->data=x;
		root->lchild=root->rchild=NULL;
		return;
	}
	if(x<root->data){
		insert(root->lchild,x);
	}else{
		insert(root->rchild,x);
	}
}
Node* create(){
	Node* root=NULL;
	for(int i=0;i<origin.size();i++){
		insert(root,origin[i]);
	}
	return root;
}
void preOrder(Node* root){
	if(root==NULL) return;
	pre.push_back(root->data);
	preOrder(root->lchild);
	preOrder(root->rchild);
}
void postOrder(Node* root){
	if(root==NULL) return;
	postOrder(root->lchild);
	postOrder(root->rchild);
	post.push_back(root->data);
}
void preMirrorOrder(Node* root){
	if(root==NULL) return;
	preMirror.push_back(root->data);
	preMirrorOrder(root->rchild);
	preMirrorOrder(root->lchild);
}
void postMirrorOrder(Node* root){
	if(root==NULL) return;
	postMirrorOrder(root->rchild);
	postMirrorOrder(root->lchild);
	postMirror.push_back(root->data);
}
int main(){
	cin>>n;
	origin.resize(n);
	for(int i=0;i<n;i++) cin>>origin[i];
	Node* root=create();

	preOrder(root);
	postOrder(root);
	preMirrorOrder(root);
	postMirrorOrder(root);

	if(origin==pre){
		cout<<"YES"<<endl;
		for(vector<int>::iterator it=post.begin();it!=post.end();it++){
			if(it!=post.begin()) cout<<" ";
			cout<<*it;
		}
		cout<<endl;
	}else if(origin==preMirror){
		cout<<"YES"<<endl;
		for(vector<int>::iterator it=postMirror.begin();it!=postMirror.end();it++){
			if(it!=postMirror.begin()) cout<<" ";
			cout<<*it;
		}
		cout<<endl;
	}else{
		cout<<"NO"<<endl;
	}
	return 0;
}

1044 Shopping in Mars(25)

Description
Shopping in Mars is quite a different experience. The Mars people pay by chained diamonds. Each diamond has a value (in Mars dollars M$). When making the payment, the chain can be cut at any position for only once and some of the diamonds are taken off the chain one by one. Once a diamond is off the chain, it cannot be taken back. For example, if we have a chain of 8 diamonds with values M$3, 2, 1, 5, 4, 6, 8, 7, and we must pay M$15. We may have 3 options:
Cut the chain between 4 and 6, and take off the diamonds from the position 1 to 5 (with values 3+2+1+5+4=15).
Cut before 5 or after 6, and take off the diamonds from the position 4 to 6 (with values 5+4+6=15).
Cut before 8, and take off the diamonds from the position 7 to 8 (with values 8+7=15).
Now given the chain of diamond values and the amount that a customer has to pay, you are supposed to list all the paying options for the customer.
If it is impossible to pay the exact amount, you must suggest solutions with minimum lost.
Input Specification
Each input file contains one test case. For each case, the first line contains 2 numbers: N ($≤10^​5$), the total number of diamonds on the chain, and M ($≤10^8$), the amount that the customer has to pay. Then the next line contains N positive numbers D1⋯DN(Di≤103 for all i=1,⋯,N) which are the values of the diamonds. All the numbers in a line are separated by a space.
Output Specification
For each test case, print i-j in a line for each pair of i ≤ j such that Di + … + Dj = M. Note that if there are more than one solution, all the solutions must be printed in increasing order of i.
If there is no solution, output i-j for pairs of i ≤ j such that Di + … + Dj >M with (Di + … + Dj−M) minimized. Again all the solutions must be printed in increasing order of i.
It is guaranteed that the total value of diamonds is sufficient to pay the given amount.
Sample Input 1
16 15
3 2 1 5 4 6 8 7 16 10 15 11 9 12 14 13
Sample Output 1
1-5
4-6
7-8
11-11
Sample Input 2
5 13
2 4 5 7 9
Sample Output 2
2-4
4-5
Program

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int inf=0x3f3f3f3f;
int n, m;
vector<int> vec;
int binarySearch(int left, int right, int x){
	while(left<right){
		int mid=(left+right)/2;
		if(vec[mid]<=x) left=mid+1;
		else right=mid;
	}
	return left;
}
int main(){
	cin>>n>>m;
	vec.resize(n+1);
	vec[0]=0;
	for(int i=1;i<=n;i++){
		cin>>vec[i];
		vec[i]+=vec[i-1];
	}
	int nearest=inf;
	for(int i=1;i<=n;i++){
		int j=binarySearch(i,n+1,vec[i-1]+m);//n+1表示越界没找到
		if(vec[j-1]-vec[i-1]==m){
			nearest=m;
			break;
		}else if(j<=n&&vec[j]-vec[i-1]<nearest){
			nearest=vec[j]-vec[i-1];
		}
	}
	for(int i=1;i<=n;i++){
		int j=binarySearch(i, n+1, vec[i-1]+nearest);
		if(vec[j-1]-vec[i-1]==nearest){
			cout<<i<<"-"<<j-1<<endl;
		}
	}
	return 0;
}

1045 Favorite Color Stripe(30)

Description
Eva is trying to make her own color stripe out of a given one. She would like to keep only her favorite colors in her favorite order by cutting off those unwanted pieces and sewing the remaining parts together to form her favorite color stripe.
It is said that a normal human eye can distinguish about less than 200 different colors, so Eva’s favorite colors are limited. However the original stripe could be very long, and Eva would like to have the remaining favorite stripe with the maximum length. So she needs your help to find her the best result.
Note that the solution might not be unique, but you only have to tell her the maximum length. For example, given a stripe of colors {2 2 4 1 5 5 6 3 1 1 5 6}. If Eva’s favorite colors are given in her favorite order as {2 3 1 5 6}, then she has 4 possible best solutions {2 2 1 1 1 5 6}, {2 2 1 5 5 5 6}, {2 2 1 5 5 6 6}, and {2 2 3 1 1 5 6}.
Input Specification
Each input file contains one test case. For each case, the first line contains a positive integer N (≤200) which is the total number of colors involved (and hence the colors are numbered from 1 to N). Then the next line starts with a positive integer M (≤200) followed by M Eva’s favorite color numbers given in her favorite order. Finally the third line starts with a positive integer L ($≤10^{​4}$) which is the length of the given stripe, followed by L colors on the stripe. All the numbers in a line a separated by a space.
Output Specification
For each test case, simply print in a line the maximum length of Eva’s favorite stripe.
Sample Input
6
5 2 3 1 5 6
12 2 2 4 1 5 5 6 3 1 1 5 6
Sample Output
7
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<map>
#include<vector>
using namespace std;
const int MAXN=10001;
map<int, int> data;
vector<int> vec;

int N,M,L;
int main(){
	cin>>N;
	cin>>M;
	for(int i=0;i<M;i++){
		int x;
		cin>>x;
		data[x]=i;
	}
	cin>>L;
	for(int i=0;i<L;i++){
		int x;
		cin>>x;
		if(data.find(x)!=data.end()){
			vec.push_back(data[x]);
		}
	}
	vector<int> dp;
	dp.resize(vec.size());
	fill(dp.begin(), dp.end(), 1);
	for(int i=0;i<vec.size();i++){
		for(int j=0;j<i;j++){
			if(vec[i]>=vec[j]&&dp[j]+1>dp[i]){
				dp[i]=dp[j]+1;
			}
		}
	}
	int maxN=0;
	for(int i=0;i<dp.size();i++){
		if(dp[i]>maxN){
			maxN=dp[i];
		}
	}
	cout<<maxN<<endl;
	return 0;
}

1046 Shortest Distance(20)

Description
The task is really simple: given N exits on a highway which forms a simple cycle, you are supposed to tell the shortest distance between any pair of exits.
Input Specification
Each input file contains one test case. For each case, the first line contains an integer N (in $[3,10^5]$), followed by N integer distances $D_1 D_2 ⋯ D_N$, where D​iis the distance between the i-th and the (i+1)-st exits, and DN is between the N-th and the 1st exits. All the numbers in a line are separated by a space. The second line gives a positive integer M ($≤10^4$), with M lines follow, each contains a pair of exit numbers, provided that the exits are numbered from 1 to N. It is guaranteed that the total round trip distance is no more than $10^7$.
Output Specification
For each test case, print your results in M lines, each contains the shortest distance between the corresponding given pair of exits.
Sample Input
5 1 2 4 14 9
3
1 3
2 5
4 1
Sample Output
3
10
7
Program

#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN=100000;
int N, M;
int dis[MAXN], d[MAXN];

int main(){
	cin>>N;
	int sum=0;

	for(int i=1;i<=N;i++){
		cin>>d[i];
		sum+=d[i];
		dis[i%N+1]=sum;
	}
	dis[1]=0;
	cin>>M;
	//注意O（M*N）会超时，如果不优化的话
	for(int i=0;i<M;i++){
		int left, right;
		cin>>left>>right;
		if(left>right) swap(left,right);
		int nowDis=dis[right]-dis[left];
		cout<<min(nowDis, sum-nowDis)<<endl;
	}
	return 0;
}

1047 Student List for Course(25)

Description
Zhejiang University has 40,000 students and provides 2,500 courses. Now given the registered course list of each student, you are supposed to output the student name lists of all the courses.
Input Specification
Each input file contains one test case. For each case, the first line contains 2 numbers: N (≤40,000), the total number of students, and K (≤2,500), the total number of courses. Then N lines follow, each contains a student’s name (3 capital English letters plus a one-digit number), a positive number C (≤20) which is the number of courses that this student has registered, and then followed by C course numbers. For the sake of simplicity, the courses are numbered from 1 to K.
Output Specification
For each test case, print the student name lists of all the courses in increasing order of the course numbers. For each course, first print in one line the course number and the number of registered students, separated by a space. Then output the students’ names in alphabetical order. Each name occupies a line.
Sample Input
10 5
ZOE1 2 4 5
ANN0 3 5 2 1
BOB5 5 3 4 2 1 5
JOE4 1 2
JAY9 4 1 2 5 4
FRA8 3 4 2 5
DON2 2 4 5
AMY7 1 5
KAT3 3 5 4 2
LOR6 4 2 4 1 5
Sample Output
1 4
ANN0
BOB5
JAY9
LOR6
2 7
ANN0
BOB5
FRA8
JAY9
JOE4
KAT3
LOR6
3 1
BOB5
4 7
BOB5
DON2
FRA8
JAY9
KAT3
LOR6
ZOE1
5 9
AMY7
ANN0
BOB5
DON2
FRA8
JAY9
KAT3
LOR6
ZOE1
Program

//下次遇到超时，直接把输入输出全换成scanf和printf
//string换成char！！！
//这两题真的体会到什么叫做string和map的慢了！
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
char names[40001][5];
vector<int> vec[2501];
bool cmp(int a,int b){
	return strcmp(names[a], names[b])<0;
}
int n, k;
int main(){
	scanf("%d %d", &n, &k);
	for(int i=0;i<n;i++){
		int m;
		scanf("%s %d", names[i],&m);
		for(int j=0;j<m;j++){
			int course;
			scanf("%d", &course);
			vec[course].push_back(i);
		}
	}
	for(int i=1;i<=k;i++){
		sort(vec[i].begin(),vec[i].end(), cmp);
		printf("%d %d\n", i,vec[i].size());
		for(int j=0;j<vec[i].size();j++) printf("%s\n",names[vec[i][j]]);
	}
	return 0;
}

1048 Find Coins(25)

Description
Eva loves to collect coins from all over the universe, including some other planets like Mars. One day she visited a universal shopping mall which could accept all kinds of coins as payments. However, there was a special requirement of the payment: for each bill, she could only use exactly two coins to pay the exact amount. Since she has as many as $10^5$ coins with her, she definitely needs your help. You are supposed to tell her, for any given amount of money, whether or not she can find two coins to pay for it.
Input Specification
Each input file contains one test case. For each case, the first line contains 2 positive numbers: N ($≤10^5$, the total number of coins) and M ($≤10^3$, the amount of money Eva has to pay). The second line contains N face values of the coins, which are all positive numbers no more than 500. All the numbers in a line are separated by a space.
Output Specification
For each test case, print in one line the two face values $V_1$ and $V_2$ (separated by a space) such that $V_1+V_​2=M$ and $V_1≤V_2$. If such a solution is not unique, output the one with the smallest $V_​1$. If there is no solution, output No Solution instead.
Sample Input 1
8 15
1 2 8 7 2 4 11 15
Sample Output 1
4 11
Sample Input 2
7 14
1 8 7 2 4 11 15
Sample Output 2
No Solution
Program

#include<iostream>
#include<vector>
using namespace std;
int hashT[1001]={0};
vector<int> vec;
int n,m;
int main(){
	cin>>n>>m;
	vec.resize(n);
	for(int i=0;i<n;i++){
		cin>>vec[i];
		hashT[vec[i]]++;
	}
	bool isPrint=false;
	for(int i=1;i<m;i++){
		if(hashT[i]&&hashT[m-i]){
			if(i==m-i&&hashT[i]==1) continue;
			cout<<i<<" "<<m-i<<endl;
			isPrint=true;
			break;
		}
	}
	if(!isPrint) cout<<"No Solution"<<endl;
	return 0;
}

1049 Counting Ones(30)

Description
The task is simple: given any positive integer N, you are supposed to count the total number of 1’s in the decimal form of the integers from 1 to N. For example, given N being 12, there are five 1’s in 1, 10, 11, and 12.
Input Specification
Each input file contains one test case which gives the positive N ($≤2^{30}$).
Output Specification
For each test case, print the number of 1’s in one line.
Sample Input
12
Sample Output
5
Program

#include<iostream>
using namespace std;
int n;
int main(){
	cin>>n;
	int left,right,k=1,ans=0,now;
	while(n/k!=0){
		left=n/(k*10);
		right=n%k;
		now=n/k%10;
		if(now==0) ans+=left*k;
		else if(now==1) ans+=left*k+right+1;
		else ans+=(left+1)*k;
		k*=10;
	}
	cout<<ans<<endl;
	return 0;
}

1050 String Subtraction(20)

Description
Given two strings $S_​1$ and $S_2$, $S=S_−S_​2$ is defined to be the remaining string after taking all the characters in $S_2$ from $S_1$. Your task is simply to calculate $S_1−S_2$ for any given strings. However, it might not be that simple to do it fast.
Input Specification
Each input file contains one test case. Each case consists of two lines which gives $S​_1$ and $S_2$, respectively. The string lengths of both strings are no more than $10^4$. It is guaranteed that all the characters are visible $ASCII$ codes and white space, and a new line character signals the end of a string.
Output Specification
For each test case, print $S_1−S_2$ in one line.
Sample Input
They are students.
aeiou
Sample Output
Thy r stdnts.
Program

#include<iostream>
#include<cstring>
using namespace std;
int hashT[256]={0};
string a, b;
int main(){
	getline(cin, a);
	getline(cin, b);
	for(int i=0;i<b.length();i++){
		hashT[b[i]]++;
	}
	for(int i=0;i<a.length();i++){
		if(hashT[a[i]]==0) cout<<a[i];
	}
	cout<<endl;
	return 0;
}

1051 Pop Sequence(25)

Description
Given a stack which can keep M numbers at most. Push N numbers in the order of 1, 2, 3, …, N and pop randomly. You are supposed to tell if a given sequence of numbers is a possible pop sequence of the stack. For example, if M is 5 and N is 7, we can obtain 1, 2, 3, 4, 5, 6, 7 from the stack, but not 3, 2, 1, 7, 5, 6, 4.
Input Specification
Each input file contains one test case. For each case, the first line contains 3 numbers (all no more than 1000): M (the maximum capacity of the stack), N (the length of push sequence), and K (the number of pop sequences to be checked). Then K lines follow, each contains a pop sequence of N numbers. All the numbers in a line are separated by a space.
Output Specification
For each pop sequence, print in one line “YES” if it is indeed a possible pop sequence of the stack, or “NO” if not.
Sample Input
5 7 5
1 2 3 4 5 6 7
3 2 1 7 5 6 4
7 6 5 4 3 2 1
5 6 4 3 7 2 1
1 7 6 5 4 3 2
Sample Output
YES
NO
NO
YES
NO
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<stack>
#include<vector>
using namespace std;
stack<int> s;
int m,n,k;
int main(){
	cin>>m>>n>>k;
	for(int i=0;i<k;i++){
		while(!s.empty()){
			s.pop();
		}
		vector<int> vec;
		for(int j=0;j<n;j++){
			int tmp;
			cin>>tmp;
			vec.push_back(tmp);
		}
		int now=0;
		for(int j=1;j<=n;j++){
			s.push(j);
			if(s.size()>m){
				break;
			}
			while(!s.empty()&&s.top()==vec[now]){
				s.pop();
				now++;
			}
		}
		if(s.empty()){
			cout<<"YES"<<endl;
		}else{
			cout<<"NO"<<endl;
		}
	}
	return 0;
}

1052 Linked List Sorting(25)

Description
A linked list consists of a series of structures, which are not necessarily adjacent in memory. We assume that each structure contains an integer key and a Next pointer to the next structure. Now given a linked list, you are supposed to sort the structures according to their key values in increasing order.
Input Specification
Each input file contains one test case. For each case, the first line contains a positive N ($<10^{5}$) and an address of the head node, where N is the total number of nodes in memory and the address of a node is a 5-digit positive integer. NULL is represented by −1.
Then N lines follow, each describes a node in the format:
Address Key Next
where Address is the address of the node in memory, Key is an integer in $[−10^{5},10​^{5}]$, and Next is the address of the next node. It is guaranteed that all the keys are distinct and there is no cycle in the linked list starting from the head node.
Output Specification
For each test case, the output format is the same as that of the input, where N is the total number of nodes in the list and all the nodes must be sorted order.
Sample Input
5 00001
11111 100 -1
00001 0 22222
33333 100000 11111
12345 -1 33333
22222 1000 12345
Sample Output
5 12345
12345 -1 00001
00001 0 11111
11111 100 22222
22222 1000 33333
33333 100000 -1
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
struct Node{
	int address;
	int data;
	int next;
	bool flag;
	Node(){}
	Node(int Address, int Data, int Next, bool Flag)
	:address(Address), data(Data), next(Next), flag(Flag){}
	bool operator < (const Node & tmp) const{
		return data < tmp.data;
	}
};
int n, head;
vector<Node> vec;
vector<Node> order;
int main(){
	cin>>n>>head;
	vec.resize(100001);
	for(int i=0;i<100001;i++) vec[i].flag=false;
	for(int i=0;i<n;i++){
		int add, data, next;
		cin>>add>>data>>next;
		vec[add] = Node(add, data, next, true);		
	}
	if(head==-1||vec[head].flag==false){
		cout<<"0 -1"<<endl;
		return 0;
	}
	while(head!=-1){
		order.push_back(vec[head]);
		head = vec[head].next;
	}
	sort(order.begin(), order.end());
	n = order.size();
	head = order[0].address;
	printf("%d %05d\n", n, head);
	for(int i=0;i<n-1;i++){
		order[i].next=order[i+1].address;
		printf("%05d %d %05d\n", order[i].address, order[i].data, order[i].next);
	}
	printf("%05d %d -1\n", order[n-1].address, order[n-1].data, order[n-1].next);
	return 0;
}

1053 Path of Equal Weight(30)

Description
Given a non-empty tree with root $R$, and with weight $W_{i}$ assigned to each tree node $T​_{i}$. The weight of a path from $R$ to $L$ is defined to be the sum of the weights of all the nodes along the path from $R$ to any leaf node $L$.
Now given any weighted tree, you are supposed to find all the paths with their weights equal to a given number. For example, let’s consider the tree showed in the following figure: for each node, the upper number is the node $ID$ which is a two-digit number, and the lower number is the weight of that node. Suppose that the given number is 24, then there exists 4 different paths which have the same given weight: {10 5 2 7}, {10 4 10}, {10 3 3 6 2} and {10 3 3 6 2}, which correspond to the red edges in the figure.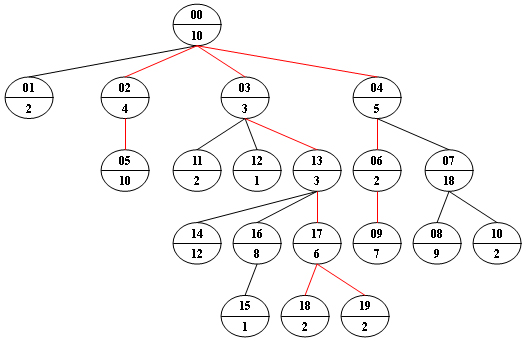

Input Specification
Each input file contains one test case. Each case starts with a line containing $0<N≤100$, the number of nodes in a tree, $M (<N)$, the number of non-leaf nodes, and $0<S<2^{30}$, the given weight number. The next line contains N positive numbers where $W_{i}(<1000)$ corresponds to the tree node $T_{i}$. Then $M$ lines follow, each in the format:
ID K ID[1] ID[2] ... ID[K]
where $ID$ is a two-digit number representing a given non-leaf node, $K$ is the number of its children, followed by a sequence of two-digit ID’s of its children. For the sake of simplicity, let us fix the root ID to be 00.
Output Specification
For each test case, print all the paths with weight $S$ in non-increasing order. Each path occupies a line with printed weights from the root to the leaf in order. All the numbers must be separated by a space with no extra space at the end of the line.
Note: sequence ${A_{1},A_{​2},⋯,A_{n}}$ is said to be greater than sequence {B1,B2,⋯,Bm} if there exists $1≤k<min{n,m}$ such that $A_{i}=B_{i} for i=1,⋯,k$, and $Ak+1>Bk+1$.
Sample Input
20 9 24
10 2 4 3 5 10 2 18 9 7 2 2 1 3 12 1 8 6 2 2
00 4 01 02 03 04
02 1 05
04 2 06 07
03 3 11 12 13
06 1 09
07 2 08 10
16 1 15
13 3 14 16 17
17 2 18 19
Sample Output
10 5 2 7
10 4 10
10 3 3 6 2
10 3 3 6 2
Program

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
using namespace std;
struct Node{
	int data;
	vector<int> child;
};

vector<Node> tree;
vector<int> vec;
int N,K,S;
bool cmp(int a,int b){
	return tree[a].data>tree[b].data;
}
void findPath(int root, int sum){
	if(tree[root].child.size()==0){
		if(sum+tree[root].data==S){
			vec.push_back(tree[root].data);
			for(int i=0;i<vec.size();i++){
				if(i!=0) cout<<" ";
				cout<<vec[i];
			}
			cout<<endl;
			vec.pop_back();
		}
		return;
	}else if(sum>=S) return;
	vec.push_back(tree[root].data);
	for(int i=0;i<tree[root].child.size();i++){
		findPath(tree[root].child[i], sum+tree[root].data);
	}
	vec.pop_back();
}
int main(){
	cin>>N>>K>>S;
	tree.resize(N);
	for(int i=0;i<N;i++) cin>>tree[i].data;
	for(int i=0;i<K;i++){
		int id,k;
		cin>>id>>k;
		for(int j=0;j<k;j++){
			int tmp;
			cin>>tmp;
			tree[id].child.push_back(tmp);
		}
		sort(tree[id].child.begin(), tree[id].child.end(), cmp);
	}
	findPath(0, 0);
	return 0;
}

1054 The Dominant Color(20)

Description
Behind the scenes in the computer’s memory, color is always talked about as a series of 24 bits of information for each pixel. In an image, the color with the largest proportional area is called the dominant color. A strictly dominant color takes more than half of the total area. Now given an image of resolution M by N (for example, 800×600), you are supposed to point out the strictly dominant color.
Input Specification
Each input file contains one test case. For each case, the first line contains 2 positive numbers: M (≤800) and N (≤600) which are the resolutions of the image. Then N lines follow, each contains M digital colors in the range $[0,2^{24})$. It is guaranteed that the strictly dominant color exists for each input image. All the numbers in a line are separated by a space.
Output Specification
For each test case, simply print the dominant color in a line.
Sample Input
5 3
0 0 255 16777215 24
24 24 0 0 24
24 0 24 24 24
Sample Output
24
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
using namespace std;
map<int, int> Map;
int n, m;
int main(){
	cin>>m>>n;
	for(int i=0;i<n;i++){
		for(int j=0;j<m;j++){
			int tmp;
			cin>>tmp;
			if(Map.find(tmp)==Map.end()) Map[tmp]=1;
			else Map[tmp]++;
		}
	}
	for(map<int, int>::iterator it=Map.begin();it!=Map.end();it++){
		if(it->second>m*n/2){
			cout<<it->first<<endl;
			return 0;
		}
	}
	return 0;
}

1055 The World’s Richest(25)

Description
Forbes magazine publishes every year its list of billionaires based on the annual ranking of the world’s wealthiest people. Now you are supposed to simulate this job, but concentrate only on the people in a certain range of ages. That is, given the net worths of N people, you must find the M richest people in a given range of their ages.
Input Specification
Each input file contains one test case. For each case, the first line contains 2 positive integers: N $(≤10​^5)$ - the total number of people, and K $(≤10^​3)$ - the number of queries. Then N lines follow, each contains the name (string of no more than 8 characters without space), age (integer in (0, 200]), and the net worth (integer in $[−10^6,10^6]$) of a person. Finally there are K lines of queries, each contains three positive integers: M (≤100) - the maximum number of outputs, and [Amin, Amax] which are the range of ages. All the numbers in a line are separated by a space.
Output Specification
For each query, first print in a line Case #X: where X is the query number starting from 1. Then output the M richest people with their ages in the range [Amin, Amax]. Each person’s information occupies a line, in the format
Name Age Net_Worth
The outputs must be in non-increasing order of the net worths. In case there are equal worths, it must be in non-decreasing order of the ages. If both worths and ages are the same, then the output must be in non-decreasing alphabetical order of the names. It is guaranteed that there is no two persons share all the same of the three pieces of information. In case no one is found, output None.
Sample Input

12 4
Zoe_Bill 35 2333
Bob_Volk 24 5888
Anny_Cin 95 999999
Williams 30 -22
Cindy 76 76000
Alice 18 88888
Joe_Mike 32 3222
Michael 5 300000
Rosemary 40 5888
Dobby 24 5888
Billy 24 5888
Nobody 5 0
4 15 45
4 30 35
4 5 95
1 45 50

Sample Output

Case #1:
Alice 18 88888
Billy 24 5888
Bob_Volk 24 5888
Dobby 24 5888
Case #2:
Joe_Mike 32 3222
Zoe_Bill 35 2333
Williams 30 -22
Case #3:
Anny_Cin 95 999999
Michael 5 300000
Alice 18 88888
Cindy 76 76000
Case #4:
None

Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
struct Node{
	string name;
	int age, net_worth;
	Node(){}
	Node(string Name, int Age, int Net_worth):name(Name), age(Age), net_worth(Net_worth){}
	bool operator < (const Node &tmp) const{
		if(net_worth!=tmp.net_worth) return net_worth>tmp.net_worth;
		else if(age!=tmp.age) return age<tmp.age;
		else return name<tmp.name;
	}
};
vector<Node> vec;
vector<Node> valid;
int n,k;
int Age[201];
int main(){
	cin>>n>>k;
	vec.resize(n);
	memset(Age, 0,sizeof(Age));
	for(int i=0;i<n;i++){
		cin>>vec[i].name>>vec[i].age>>vec[i].net_worth;
	}
	sort(vec.begin(), vec.end());
	for(int i=0;i<n;i++){
		if(Age[vec[i].age]<100){
			Age[vec[i].age]++;
			valid.push_back(vec[i]);
		}
	}
	int m,amin,amax;
	for(int i=0;i<k;i++){
		cin>>m>>amin>>amax;
		cout<<"Case #"<<i+1<<":"<<endl;
		int printNum=0;
		for(int j=0;j<valid.size()&&printNum<m;j++){
			if(valid[j].age>=amin&&valid[j].age<=amax){
				cout<<valid[j].name<<" "<<valid[j].age<<" "<<valid[j].net_worth<<endl;
				printNum++;
			}
		}
		if(printNum==0) cout<<"None"<<endl;
	}
	return 0;
}

1056 Mice and Rice(25)

Description
Mice and Rice is the name of a programming contest in which each programmer must write a piece of code to control the movements of a mouse in a given map. The goal of each mouse is to eat as much rice as possible in order to become a FatMouse.
First the playing order is randomly decided for Np programmers. Then every NG programmers are grouped in a match. The fattest mouse in a group wins and enters the next turn. All the losers in this turn are ranked the same. Every NG winners are then grouped in the next match until a final winner is determined.
For the sake of simplicity, assume that the weight of each mouse is fixed once the programmer submits his/her code. Given the weights of all the mice and the initial playing order, you are supposed to output the ranks for the programmers.
Input Specification
Each input file contains one test case. For each case, the first line contains 2 positive integers: NP and N​G (≤1000), the number of programmers and the maximum number of mice in a group, respectively. If there are less than N​G mice at the end of the player’s list, then all the mice left will be put into the last group. The second line contains NP distinct non-negative numbers Wi (i=0,⋯,NP−1) where each W​i
​​ is the weight of the i-th mouse respectively. The third line gives the initial playing order which is a permutation of 0,⋯,N​P−1(assume that the programmers are numbered from 0 to NP−1). All the numbers in a line are separated by a space.
Output Specification
For each test case, print the final ranks in a line. The i-th number is the rank of the i-th programmer, and all the numbers must be separated by a space, with no extra space at the end of the line.
Sample Input
11 3
25 18 0 46 37 3 19 22 57 56 10
6 0 8 7 10 5 9 1 4 2 3
Sample Output
5 5 5 2 5 5 5 3 1 3 5
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
struct Mice{
	int weight;
	int rank;
	int result_rank;
};
vector<Mice> vec;
vector<int> vecR;
queue<int> q;
int nq, ng;
bool cmp(int a, int b){
	return vec[a].rank>vec[b].rank;
}
int main(){
	cin>>nq>>ng;
	vec.resize(nq);
	for(int i=0;i<nq;i++) cin>>vec[i].weight;
	int tmp;
	for(int i=0;i<nq;i++){
		cin>>tmp;
		q.push(tmp);
		vecR.push_back(i);
	}
	int rank=0;
	int Nq=nq;
	int index=0;
	int tmpN=0;
	while(q.size()!=1){		
		int up;
		int Max=0;
		for(int i=0;index<Nq&&i<ng;i++,index++){
			int front=q.front();
			q.pop();
			if(vec[front].weight>Max){
				up=front;
				Max=vec[front].weight;
			}
			vec[front].rank=rank;
		}
		vec[up].rank=rank+1;
		q.push(up);
		tmpN++;
		if(index==Nq){
			index=0;
			Nq=tmpN;
			tmpN=0;
			rank++;
		}
	}
	sort(vecR.begin(), vecR.end(), cmp);
	vec[vecR[0]].result_rank=1;
	for(int i=1;i<nq;i++){
		if(vec[vecR[i]].rank==vec[vecR[i-1]].rank){
			vec[vecR[i]].result_rank=vec[vecR[i-1]].result_rank;
		}else{
			vec[vecR[i]].result_rank=i+1;
		}
	}
	for(int i=0;i<nq;i++){
		if(i!=0) cout<<" ";
		cout<<vec[i].result_rank;
	}
	cout<<endl;
	return 0;
}

1057 Stack(30)

Description
Stack is one of the most fundamental data structures, which is based on the principle of Last In First Out (LIFO). The basic operations include Push (inserting an element onto the top position) and Pop (deleting the top element). Now you are supposed to implement a stack with an extra operation: PeekMedian – return the median value of all the elements in the stack. With N elements, the median value is defined to be the (N/2)-th smallest element if N is even, or ((N+1)/2)-th if N is odd.
Input Specification
Each input file contains one test case. For each case, the first line contains a positive integer N ($≤10^{5}$). Then N lines follow, each contains a command in one of the following 3 formats:
Push key
Pop
PeekMedian
where key is a positive integer no more than $10^{5}$.
Output Specification
For each Push command, insert key into the stack and output nothing. For each Pop or PeekMedian command, print in a line the corresponding returned value. If the command is invalid, print Invalid instead.
Sample Input
17
Pop
PeekMedian
Push 3
PeekMedian
Push 2
PeekMedian
Push 1
PeekMedian
Pop
Pop
Push 5
Push 4
PeekMedian
Pop
Pop
Pop
Pop
Sample Output
Invalid
Invalid
3
2
2
1
2
4
4
5
3
Invalid
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<stack>
using namespace std;
const int MAXN=100010;
const int SQRN=316;
stack<int> st;
int block[SQRN];
int table[MAXN];
void peekMedian(int K){
	int sum=0;
	int idx=0;
	while(sum+block[idx]<K){
		sum+=block[idx++];
	}
	int num=idx*SQRN;
	while(sum+table[num]<K){
		sum+=table[num++];
	}
	cout<<num<<endl;
}
void Push(int x){
	st.push(x);
	block[x / SQRN] ++;
	table[x]++;
}
void Pop(){
	int x=st.top();
	st.pop();
	block[x /SQRN]--;
	table[x]--;
	cout<<x<<endl;
}
int main(){
	int x, query;
	memset(block, 0, sizeof(block));
	memset(table, 0, sizeof(table));
	string str;
	cin>>query;
	for(int i=0;i<query;i++){
		cin>>str;
		if(str=="Push"){
			cin>>x;
			Push(x);
		}else if(str=="Pop"){
			if(st.empty()){
				cout<<"Invalid"<<endl;
			}else Pop();
		}else if(str=="PeekMedian"){
			if(st.empty()) cout<<"Invalid"<<endl;
			else{
				int K=st.size();
				if(K%2==0) K/=2;
				else K=(K+1)/2;
				peekMedian(K);
			}
		}
	}
}

#include<iostream>
#include<algorithm>
#include<cstring>
#include<stack>
#define lowbit(i) ((i)&(-i))
using namespace std;
const int MAXN=100010;
int C[MAXN];
void update(int x, int v){
	for(int i=x;i<MAXN;i+=lowbit(i)) C[i]+=v;
}
int getSum(int x){
	int sum=0;
	for(int i=x;i>0;i-=lowbit(i)) sum+=C[i];
	return sum;
}
void PeekMedian(int K){
	int l=1, r=MAXN, mid;
	while(l<r){
		mid=(l+r)/2;
		if(getSum(mid)>=K) r=mid;
		else l=mid+1;
	}
	cout<<l<<endl;
}
stack<int> st;
int N, x;
string str;
int main(){
	cin>>N;
	memset(C,0,sizeof(C));
	while(N--){
		cin>>str;
		if(str=="Push"){
			cin>>x;
			st.push(x);
			update(x, 1);
		}else if(str=="Pop"){
			if(st.size()==0) cout<<"Invalid"<<endl;
			else{
				int x=st.top();
				st.pop();
				update(x, -1);
				cout<<x<<endl;
			}
		}else if(str=="PeekMedian"){
			if(st.size()==0) cout<<"Invalid"<<endl;
			else{
				int n=st.size();
				if(n%2==0) PeekMedian(n/2);
				else PeekMedian((n+1)/2);
			}
		}
	}
	return 0;
}

1058 A+B in Hogwarts(20)

Description
If you are a fan of Harry Potter, you would know the world of magic has its own currency system – as Hagrid explained it to Harry, “Seventeen silver Sickles to a Galleon and twenty-nine Knuts to a Sickle, it’s easy enough.” Your job is to write a program to compute A+B where A and B are given in the standard form of Galleon.Sickle.Knut (Galleon is an integer in $[0,10^7]$, Sickle is an integer in $[0, 17)$, and Knut is an integer in $[0, 29)$).
Input Specification
Each input file contains one test case which occupies a line with A and B in the standard form, separated by one space.
Output Specification
For each test case you should output the sum of A and B in one line, with the same format as the input.
Sample Input
3.2.1 10.16.27
Sample Output
14.1.28
Program

#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const int BASE2=17,BASE3=29;
struct Node{
	int x1, x2, x3;
	Node(){}
	Node(int y1, int y2, int y3):x1(y1),x2(y2),x3(y3){}
	void toString(){
		cout<<x1<<"."<<x2<<"."<<x3<<endl;
	}
};
Node cal(Node A, Node B){
	Node result;
	result.x3=(A.x3+B.x3)%BASE3;
	result.x2=(A.x2+B.x2+(A.x3+B.x3)/BASE3)%BASE2;
	result.x1=(A.x1+B.x1+(A.x2+B.x2+(A.x3+B.x3)/BASE3)/BASE2);
	return result;
}
int main(){
	Node A(0,0,0), B(0,0,0);
	scanf("%d.%d.%d %d.%d.%d", &A.x1, &A.x2,&A.x3, &B.x1, &B.x2, &B.x3);
	cal(A,B).toString();
	return 0;
}

1059 Prime Factors(25)

Description
Given any positive integer N, you are supposed to find all of its prime factors, and write them in the format $N = p_1^{k\1}×p_2^{k_2}×⋯×p_​m^{​_km}$.
Input Specification
Each input file contains one test case which gives a positive integer N in the range of long int.
Output Specification
Factor N in the format N = p1^k​1*p2^k​2*…*p​m^km, where p​i’s are prime factors of N in increasing order, and the exponent ki is the number of pi – hence when there is only one pi, ki is 1 and must NOT be printed out.
Sample Input
97532468
Sample Output
97532468=2^2*11*17*101*1291
Program

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
using namespace std;
const long MAXN=10001;
long n;
vector<int> primes;
bool vis[MAXN];
void findPrime(){
	memset(vis, false, sizeof(vis));
	for(long i=2;i<MAXN;i++){
		if(!vis[i]){
			vis[i]=true;
			primes.push_back(i);
		}
		for(long j=0;j<primes.size()&&i*primes[j]<MAXN;j++){
			vis[i*primes[j]]=true;
			if(i%primes[j]==0) break;
		}
	}
}
int main(){
	findPrime();
	cin>>n;
	cout<<n<<"=";
	if(n==1){
		cout<<1<<endl;
		return 0;
	}
	bool bFirst=true;
	for(long i=0;i<primes.size();i++){
		int p=0;
		while(n%primes[i]==0){
			p++;
			n/=primes[i];
		}
		if(p>0){
			if(bFirst) bFirst=false;
			else cout<<"*";
			cout<<primes[i];
			if(p>1) cout<<"^"<<p;
		}		
	}
	cout<<endl;
	return 0;
}

1060 Are They Equal (25)

Description
If a machine can save only 3 significant digits, the float numbers 12300 and 12358.9 are considered equal since they are both saved as $0.123×10^{​5}$ with simple chopping. Now given the number of significant digits on a machine and two float numbers, you are supposed to tell if they are treated equal in that machine.
Input Specification
Each input file contains one test case which gives three numbers N, A and B, where N (<100) is the number of significant digits, and A and B are the two float numbers to be compared. Each float number is non-negative, no greater than $10^{100}$, and that its total digit number is less than 100.
Output Specification
For each test case, print in a line YES if the two numbers are treated equal, and then the number in the standard form 0.d[1]...d[N]*10^k (d[1]>0 unless the number is 0); or NO if they are not treated equal, and then the two numbers in their standard form. All the terms must be separated by a space, with no extra space at the end of a line.
Note: Simple chopping is assumed without rounding.
Sample Input 1
3 12300 12358.9
Sample Output 1
YES 0.123*10^5
Sample Input 2
3 120 128
Sample Output 2
NO 0.120*10^3 0.128*10^3
Program

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int n;
string s1, s2;
string transform(string s, int &e){
	string result;
	while(s.length()>1&&s[0]=='0'){
		s.erase(0, 1);
	}
	if(s[0]=='.'){
		s.erase(0, 1);
		while(s.length()>1&&s[0]=='0'){
			s.erase(0, 1);
			e--;
		}
	}else{
		int k=0;
		while(k<s.length()&&s[k]!='.') {
			k++;
			e++;
		}
		if(k!=s.length()){
			s.erase(k, 1);
		}
	}

	for(int i=0;i<n;i++){
		if(i<s.length()) result+=s[i];
		else result+='0';
	}
	if(s.length()==1&&s[0]=='0') e=0;
	return result;
}
bool isEqual(string s1, string s2){
	for(int i=0;i<n;i++){
		if(s1[i]!=s2[i]) return false;
	}
	return true;
}
int main(){
	cin>>n>>s1>>s2;
	int e1, e2;
	e1=e2=0;
	string ss1=transform(s1, e1);
	string ss2=transform(s2, e2);
	if(isEqual(ss1, ss2)&&e1==e2){
		cout<<"YES 0."<<ss1<<"*10^"<<e1<<endl;
	}else{
		cout<<"NO 0."<<ss1<<"*10^"<<e1<<" 0."<<ss2<<"*10^"<<e2<<endl;
	}
	return 0;
}

1061 Dating(20)

Description
Sherlock Holmes received a note with some strange strings: Let’s date! 3485djDkxh4hhGE 2984akDfkkkkggEdsb s&hgsfdk d&Hyscvnm. It took him only a minute to figure out that those strange strings are actually referring to the coded time Thursday 14:04 – since the first common capital English letter (case sensitive) shared by the first two strings is the 4th capital letter D, representing the 4th day in a week; the second common character is the 5th capital letter E, representing the 14th hour (hence the hours from 0 to 23 in a day are represented by the numbers from 0 to 9 and the capital letters from A to N, respectively); and the English letter shared by the last two strings is s at the 4th position, representing the 4th minute. Now given two pairs of strings, you are supposed to help Sherlock decode the dating time.
Input Specification**
Each input file contains one test case. Each case gives 4 non-empty strings of no more than 60 characters without white space in 4 lines.
**Output Specification
For each test case, print the decoded time in one line, in the format DAY HH:MM, where DAY is a 3-character abbreviation for the days in a week – that is, MON for Monday, TUE for Tuesday, WED for Wednesday, THU for Thursday, FRI for Friday, SAT for Saturday, and SUN for Sunday. It is guaranteed that the result is unique for each case.
Sample Input
3485djDkxh4hhGE
2984akDfkkkkggEdsb
s&hgsfdk
d&Hyscvnm
Sample Output
THU 14:04
Program

#include<iostream>
#include<cctype>
#include<cstring>
#include<cmath>
#include<iomanip>
#include<string>
using namespace std;
const char *Data[]={"MON","TUE","WED","THU","FRI","SAT","SUN"};
int main()
{
	//cout<<Data[1];
	int flag=0,n,l;
	string strings[4];
	int save;
	for(int i=0;i<4;i++){
		cin>>strings[i];

	}
	for(int i=0;i<(strings[0].length()<=strings[1].length()?strings[0].length():strings[1].length());i++){
		if(strings[0][i]==strings[1][i]&&isupper(strings[0][i])&&flag==0&&strings[0][i]<'H'){
			n=strings[0][i]-'A';
			flag++;
		}else if(strings[0][i]==strings[1][i]&&flag==1&&isalnum(strings[0][i])){
			if(isdigit(strings[0][i])){
				save=strings[0][i]-'0';
				flag++;
				break;
			}else if(isupper(strings[0][i])&&strings[0][i]<'O'){
				save=strings[0][i]-'7';
				flag++;
				break;
			}
		}
	}
	flag=0;
	for(int i=0;i<(strings[2].length()<=strings[3].length()?strings[2].length():strings[3].length());i++){
		if(strings[2][i]==strings[3][i]&&isalpha(strings[2][i])){
			l=i;
			flag++;
			break;
		}
	}

	cout<<Data[n]<<" "<<setw(2)<<setfill('0')<<save<<":"<<setw(2)<<setfill('0')<<l;
	return 0;
}

1062 Talent and Virtue(25)

Description
About 900 years ago, a Chinese philosopher Sima Guang wrote a history book in which he talked about people’s talent and virtue. According to his theory, a man being outstanding in both talent and virtue must be a “sage（圣人）”; being less excellent but with one’s virtue outweighs talent can be called a “nobleman（君子）”; being good in neither is a “fool man（愚人）”; yet a fool man is better than a “small man（小人）” who prefers talent than virtue.
Now given the grades of talent and virtue of a group of people, you are supposed to rank them according to Sima Guang’s theory.
Input Specification
Each input file contains one test case. Each case first gives 3 positive integers in a line: $N (≤10^{5})$, the total number of people to be ranked; $L (≥60)$, the lower bound of the qualified grades – that is, only the ones whose grades of talent and virtue are both not below this line will be ranked; and $H (<100)$, the higher line of qualification – that is, those with both grades not below this line are considered as the “sages”, and will be ranked in non-increasing order according to their total grades. Those with talent grades below H but virtue grades not are cosidered as the “noblemen”, and are also ranked in non-increasing order according to their total grades, but they are listed after the “sages”. Those with both grades below H, but with virtue not lower than talent are considered as the “fool men”. They are ranked in the same way but after the “noblemen”. The rest of people whose grades both pass the L line are ranked after the “fool men”.
Then N lines follow, each gives the information of a person in the format:
ID_Number Virtue_Grade Talent_Grade
where ID_Number is an 8-digit number, and both grades are integers in $[0, 100]$. All the numbers are separated by a space.
Output Specification
The first line of output must give $M (≤N)$, the total number of people that are actually ranked. Then $M$ lines follow, each gives the information of a person in the same format as the input, according to the ranking rules. If there is a tie of the total grade, they must be ranked with respect to their virtue grades in non-increasing order. If there is still a tie, then output in increasing order of their ID’s.
Sample Input
14 60 80
10000001 64 90
10000002 90 60
10000011 85 80
10000003 85 80
10000004 80 85
10000005 82 77
10000006 83 76
10000007 90 78
10000008 75 79
10000009 59 90
10000010 88 45
10000012 80 100
10000013 90 99
10000014 66 60
Sample Output
12
10000013 90 99
10000012 80 100
10000003 85 80
10000011 85 80
10000004 80 85
10000007 90 78
10000006 83 76
10000005 82 77
10000002 90 60
10000014 66 60
10000008 75 79
10000001 64 90
Program

#include <stdio.h>  
#include <iostream>  
#include <vector>  
#include <algorithm>  
using namespace std;
struct Student {
	int num;
	int d;
	int c;
	bool operator < (const Student &A) const {
		if (d + c != A.d + A.c)
			return d + c > A.d + A.c;
		else {
			if (d != A.d)
				return d > A.d;
			else
				return num < A.num;
		}
	}
};

int main() {
	int n, l, h, count = 0;
	Student tmp;
	vector<Student> v1, v2, v3, v4;
	scanf("%d%d%d", &n, &l, &h);
	int x, y, z;
	for (int i = 0; i < n; i++) {
		scanf("%d%d%d", &x, &y, &z);
		tmp.num = x;
		tmp.d = y;
		tmp.c = z;
		if (y >= l && z >= l) {
			count++;
			if (y >= h && z >= h) {
				v1.push_back(tmp);
			}
			else if (y >= h && z < h) {
				v2.push_back(tmp);
			}
			else if (y < h && z < h && y >= z) {
				v3.push_back(tmp);
			}
			else {
				v4.push_back(tmp);
			}
		}
	}
	sort(v1.begin(), v1.end());
	sort(v2.begin(), v2.end());
	sort(v3.begin(), v3.end());
	sort(v4.begin(), v4.end());
	cout << count << endl;
	vector<Student>::iterator itr;
	for (itr = v1.begin(); itr != v1.end(); ++itr)
		printf("%d %d %d\n", itr->num, itr->d, itr->c);
	for (itr = v2.begin(); itr != v2.end(); ++itr)
		printf("%d %d %d\n", itr->num, itr->d, itr->c);
	for (itr = v3.begin(); itr != v3.end(); ++itr)
		printf("%d %d %d\n", itr->num, itr->d, itr->c);
	for (itr = v4.begin(); itr != v4.end(); ++itr)
		printf("%d %d %d\n", itr->num, itr->d, itr->c);
	return 0;
}

1063 Set Similarity(25)

Description
Given two sets of integers, the similarity of the sets is defined to be $N_c/N_t×100%$, where Nc is the number of distinct common numbers shared by the two sets, and Nt is the total number of distinct numbers in the two sets. Your job is to calculate the similarity of any given pair of sets.
Input Specification
Each input file contains one test case. Each case first gives a positive integer N (≤50) which is the total number of sets. Then N lines follow, each gives a set with a positive M ($≤10^{4}$) and followed by M integers in the range [0,10^{9}]. After the input of sets, a positive integer K (≤2000) is given, followed by K lines of queries. Each query gives a pair of set numbers (the sets are numbered from 1 to N). All the numbers in a line are separated by a space.
Output Specification
For each query, print in one line the similarity of the sets, in the percentage form accurate up to 1 decimal place.
Sample Input
3
3 99 87 101
4 87 101 5 87
7 99 101 18 5 135 18 99
2
1 2
1 3
Sample Output
50.0%
33.3%
Program

#include<iostream>
#include<algorithm>
#include<set>
#include<cstring>
using namespace std;
set<int> st[51];
int n;
float cmp(int a,int b){
	int total=0, common=0;
	for(set<int>::iterator it=st[a].begin();it!=st[a].end();it++){
		if(st[b].find(*it)!=st[b].end()) common++;
	}
	total=st[a].size()+st[b].size()-common;
	return common*100.0/total;
}
int main(){
	cin>>n;
	for(int i=0;i<n;i++){
		int m;
		cin>>m;
		for(int j=0;j<m;j++){
			int tmp;
			cin>>tmp;
			st[i].insert(tmp);
		}
	}
	cin>>n;
	for(int i=0;i<n;i++){
		int a, b;
		cin>>a>>b;
		float result=cmp(a-1,b-1);
		printf("%.1f%\n", result);
	}
	return 0;
}

1064 Complete Binary Search Tree(30)

Description
A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

• The left subtree of a node contains only nodes with keys less than the node’s key.
• The right subtree of a node contains only nodes with keys greater than or equal to the node’s key.
• Both the left and right subtrees must also be binary search trees.
  A Complete Binary Tree (CBT) is a tree that is completely filled, with the possible exception of the bottom level, which is filled from left to right.
  Now given a sequence of distinct non-negative integer keys, a unique BST can be constructed if it is required that the tree must also be a CBT. You are supposed to output the level order traversal sequence of this BST.

Input Specification
Each input file contains one test case. For each case, the first line contains a positive integer N (≤1000). Then N distinct non-negative integer keys are given in the next line. All the numbers in a line are separated by a space and are no greater than 2000.
Output Specification
For each test case, print in one line the level order traversal sequence of the corresponding complete binary search tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line.
Sample Input
10
1 2 3 4 5 6 7 8 9 0
Sample Output
6 3 8 1 5 7 9 0 2 4
Program

/*
给定二叉排序树的前序中序后序，都可以通过此方法构建完全二叉树
*/
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int N;
vector<int> vec, CBT;
int index=0;
void inOrder(int root){
	if(root>=N) return;
	inOrder(root*2+1);
	CBT[root]=vec[index++];
	inOrder(root*2+2);
}
int main(){
	cin>>N;
	vec.resize(N);
	CBT.resize(N);
	for(int i=0;i<N;i++) cin>>vec[i];
	sort(vec.begin(), vec.end());
	inOrder(0);
	for(int i=0;i<N;i++){
		if(i!=0) cout<<" ";
		cout<<CBT[i];
	}
	cout<<endl;
	return 0;
}

1065 A+B and C(64bit) (20)

Description
Given three integers A, B and C in $[−2^{63},2^{63})$, you are supposed to tell whether A+B>C.
Input Specification
The first line of the input gives the positive number of test cases, T (≤10). Then T test cases follow, each consists of a single line containing three integers A, B and C, separated by single spaces.
Output Specification
For each test case, output in one line Case #X: true if A+B>C, or Case #X: false otherwise, where X is the case number (starting from 1).
Sample Input
3
1 2 3
2 3 4
9223372036854775807 -9223372036854775808 0
Sample Output
Case #1: false
Case #2: true
Case #3: false
Program

#include<iostream>
#include<cstring>
using namespace std;
const string result[2]={"false","true"};
int T;
long long A, B, C;

int main(){
	cin>>T;
	for(int i=1;i<=T;i++){
		cin>>A>>B>>C;
		long long sum = A + B;
		bool flag=false;
		if(A>0&&B>0&&sum<0) flag=true;
		else if(A<0&&B<0&&sum>=0) flag=false;
		else if(sum>C) flag=true;
		else flag=false;
		cout<<"Case #"<<i<<": "<<result[flag]<<endl;
	}
	return 0;
}

1066 Root of AVL Tree(25)

Description
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.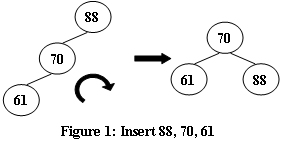
)
)
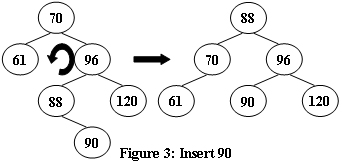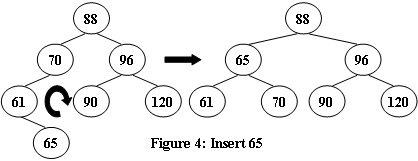
Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.
Input Specification
Each input file contains one test case. For each case, the first line contains a positive integer N (≤20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.
Output Specification
For each test case, print the root of the resulting AVL tree in one line.
Sample Input 1
5
88 70 61 96 120
Sample Output 1
70
Sample Input 2
7
88 70 61 96 120 90 65
Sample Output 2
88
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<cmath>
using namespace std;
struct Node{
	int data;
	int height;
	Node *lchild, *rchild;
};
int getHeight(Node *root){
	if(root==NULL) return 0;
	return root->height;
}
int getBalancedFactor(Node *root){
	return getHeight(root->lchild) - getHeight(root->rchild);
}
void updateHeight(Node *root){
	root->height = max(getHeight(root->lchild), getHeight(root->rchild)) + 1;
}
void leftRotation(Node* &root){
	Node* tmp=root->rchild;
	root->rchild=tmp->lchild;
	tmp->lchild=root;
	updateHeight(root);
	updateHeight(tmp);
	root=tmp;
}
void rightRotation(Node* &root){
	Node* tmp=root->lchild;
	root->lchild=tmp->rchild;
	tmp->rchild=root;
	updateHeight(root);
	updateHeight(tmp);
	root=tmp;
}
Node* newNode(int x){
	Node* root=new Node;
	root->data=x;
	root->height=1;
	root->lchild=root->rchild=NULL;
	return root;
}
void insert(Node* &root, int x){
	if(root==NULL){
		root=newNode(x);
		return;
	}
	if(x<root->data){
		insert(root->lchild, x);
		updateHeight(root);
		if(getBalancedFactor(root)==2){
			if(getBalancedFactor(root->lchild)==1){
				rightRotation(root);
			}else{
				leftRotation(root->lchild);
				rightRotation(root);
			}
		}
	}else{
		insert(root->rchild, x);
		updateHeight(root);
		if(getBalancedFactor(root)==-2){
			if(getBalancedFactor(root->rchild)==-1){
				leftRotation(root);
			}else{
				rightRotation(root->rchild);
				leftRotation(root);
			}
		}
	}
}
int N;
int main(){
	cin>>N;
	Node* root=NULL;
	for(int i=0;i<N;i++){
		int tmp;
		cin>>tmp;
		insert(root, tmp);
	}
	cout<<root->data<<endl;
	return 0;
}

1067 Sort with Swap(0, i)(25)

Description
Given any permutation of the numbers {0, 1, 2,…, N−1}, it is easy to sort them in increasing order. But what if Swap(0, *) is the ONLY operation that is allowed to use? For example, to sort {4, 0, 2, 1, 3} we may apply the swap operations in the following way:
Swap(0, 1) => {4, 1, 2, 0, 3}
Swap(0, 3) => {4, 1, 2, 3, 0}
Swap(0, 4) => {0, 1, 2, 3, 4}
Now you are asked to find the minimum number of swaps need to sort the given permutation of the first N nonnegative integers.
Input Specification
Each input file contains one test case, which gives a positive N ($≤10^5$) followed by a permutation sequence of {0, 1, …, N−1}. All the numbers in a line are separated by a space.
Output Specification
For each case, simply print in a line the minimum number of swaps need to sort the given permutation.
Sample Inpu
10
3 5 7 2 6 4 9 0 8 1
Sample Output
9
Program

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int pos[100001];
int n;
int main(){
	cin>>n;
	int tmp;
	int wrong=0;
	for(int i=0;i<n;i++){
		cin>>tmp;
		pos[tmp]=i;
		if(i!=tmp) wrong++;

	}
	int num=0;
	int k=1;
	while(wrong>0){
		if(pos[0]!=0){
			swap(pos[0],pos[pos[0]]);
			wrong--;
			num++;
			if(pos[0]==0) wrong--;
		}else{
			while(k<n){
				if(pos[k]!=k){
					swap(pos[0], pos[k]);
					wrong++;
					num++;
					break;
				}
				k++;
			}
		}
	}
	cout<<num<<endl;
	return 0;
}

1068 Find More Coins(30)

Description
Eva loves to collect coins from all over the universe, including some other planets like Mars. One day she visited a universal shopping mall which could accept all kinds of coins as payments. However, there was a special requirement of the payment: for each bill, she must pay the exact amount. Since she has as many as $10^{4}$ coins with her, she definitely needs your help. You are supposed to tell her, for any given amount of money, whether or not she can find some coins to pay for it.
Input Specification
Each input file contains one test case. For each case, the first line contains 2 positive numbers: N ($≤10^{​4}$), the total number of coins) and M ($≤10^{2}$), the amount of money Eva has to pay). The second line contains N face values of the coins, which are all positive numbers. All the numbers in a line are separated by a space.
Output Specification
For each test case, print in one line the face values $V1≤V2≤⋯≤Vk$ such that$ V1+V2+⋯+Vk=M$. All the numbers must be separated by a space, and there must be no extra space at the end of the line. If such a solution is not unique, output the smallest sequence. If there is no solution, output “No Solution” instead.
Note: sequence ${A[1], A[2], …}$ is said to be “smaller” than sequence ${B[1], B[2], …}$ if there exists k≥1 such that $A[i]=B[i]$ for all $i<k$, and $A[k] < B[k]$.
Sample Input 1
8 9
5 9 8 7 2 3 4 1
Sample Output 1
1 3 5
Sample Input 2
4 8
7 2 4 3
Sample Output 2
No Solution
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<functional>
#include<vector>
using namespace std;
const int MAXN=10001;
const int MAXV=101;
int N,M;
int dp[MAXV];
int w[MAXN];
int choice[MAXN][MAXV];
int main(){
	cin>>N>>M;
	memset(dp, 0, sizeof(dp));
	for(int i=1;i<=N;i++) cin>>w[i];
	sort(w+1, w+N+1, greater<int>());

	for(int i=1;i<=N;i++){
		for(int v=M;v>=w[i];v--){
			if(dp[v]<=dp[v-w[i]]+w[i]){
				dp[v]=dp[v-w[i]]+w[i];
				choice[i][v]=1;
			}else{
				choice[i][v]=0;
			}
		}
	}
	if(dp[M]!=M) cout<<"No Solution"<<endl;
	else{
		vector<int> vec;
		int v=M;
		for(int i=N;i>=1;i--){
			if(choice[i][v]==1){
				v-=w[i];
				vec.push_back(w[i]);
			}
		}
		for(int i=0;i<vec.size();i++){
			if(i!=0) cout<<" ";
			cout<<vec[i];
		}
		cout<<endl;
	}
	return 0;
}

1069 The Black Hole of Numbers(20)

Description
For any 4-digit integer except the ones with all the digits being the same, if we sort the digits in non-increasing order first, and then in non-decreasing order, a new number can be obtained by taking the second number from the first one. Repeat in this manner we will soon end up at the number 6174 – the black hole of 4-digit numbers. This number is named Kaprekar Constant.
For example, start from 6767, we’ll get:
7766 - 6677 = 1089
9810 - 0189 = 9621
9621 - 1269 = 8352
8532 - 2358 = 6174
7641 - 1467 = 6174
… …
Given any 4-digit number, you are supposed to illustrate the way it gets into the black hole.
Input Specification
Each input file contains one test case which gives a positive integer N in the range $(0,10^4)$.
Output Specification
If all the 4 digits of N are the same, print in one line the equation N - N = 0000. Else print each step of calculation in a line until 6174 comes out as the difference. All the numbers must be printed as 4-digit numbers.
Sample Input 1
6767
Sample Output 1
7766 - 6677 = 1089
9810 - 0189 = 9621
9621 - 1269 = 8352
8532 - 2358 = 6174
Sample Input 2
2222
Sample Output 2
2222 - 2222 = 0000
Program

#include<iostream>
#include<cstring>
#include<algorithm>
#include<functional>
#include<string>
#include<cstdlib>
#include<stdlib.h>
#include<cstdio>
using namespace std;
string str;
int main(){
	while(cin>>str){
		while(str.length()<4){
			str="0"+str;
		}
		if(str.find_first_not_of(str[0])==string::npos){
			cout<<str<<" - "<<str<<" = 0000"<<endl;
			continue;
		}
		int max,min;
		do{
			sort(str.begin(), str.end(), greater<char>());
			max=stoi(str);
			cout<<str<<" - ";
			sort(str.begin(), str.end(), less<char>());
			min=stoi(str);

			cout<<str<<" = ";
			str = to_string(max-min);
			while(str.length()<4){
				str="0"+str;
			}
			cout<<str<<endl;
		}while(str!="6174");
	}


	return 0;
}

1070 Mooncake(25)

Description
Mooncake is a Chinese bakery product traditionally eaten during the Mid-Autumn Festival. Many types of fillings and crusts can be found in traditional mooncakes according to the region’s culture. Now given the inventory amounts and the prices of all kinds of the mooncakes, together with the maximum total demand of the market, you are supposed to tell the maximum profit that can be made.
Note: partial inventory storage can be taken. The sample shows the following situation: given three kinds of mooncakes with inventory amounts being 180, 150, and 100 thousand tons, and the prices being 7.5, 7.2, and 4.5 billion yuans. If the market demand can be at most 200 thousand tons, the best we can do is to sell 150 thousand tons of the second kind of mooncake, and 50 thousand tons of the third kind. Hence the total profit is 7.2 + 4.5/2 = 9.45 (billion yuans).
Input Specification
Each input file contains one test case. For each case, the first line contains 2 positive integers N (≤1000), the number of different kinds of mooncakes, and D (≤500 thousand tons), the maximum total demand of the market. Then the second line gives the positive inventory amounts (in thousand tons), and the third line gives the positive prices (in billion yuans) of N kinds of mooncakes. All the numbers in a line are separated by a space.
Output Specification
For each test case, print the maximum profit (in billion yuans) in one line, accurate up to 2 decimal places.
Sample Input
3 200
180 150 100
7.5 7.2 4.5
Sample Output
9.45
Program

#include<iostream>
#include<vector>
#include<algorithm>
#include<iomanip>
using namespace std;
struct Moon {
	double stock;
	double value;
	double price;
};
bool cmp(Moon a, Moon b) {
	return a.price > b.price;
}
int main(){
	int N, MAX, index = 0;
	double sum = 0;
	cin >> N >> MAX;

	Moon y;
	vector<Moon> x;
	for (int i = 0; i < N; i++){
		cin >> y.stock;

		x.push_back(y);
	}
	for (int i = 0; i < N; i++){
		cin >> x[i].value;

		x[i].price = x[i].value / x[i].stock;
	}
	sort(x.begin(), x.end(), cmp);
	while (MAX != 0 && index != N){
		if (MAX >= x[index].stock){
			MAX -= x[index].stock;
			sum += x[index].value;
		}
		else{
			sum += x[index].price*MAX;
			MAX = 0;
		}
		index++;
	}

	cout << setiosflags(ios::fixed) << setprecision(2) << sum;
	return 0;
}

1071 Speech Patterns(25)

Description
People often have a preference among synonyms of the same word. For example, some may prefer “the police”, while others may prefer “the cops”. Analyzing such patterns can help to narrow down a speaker’s identity, which is useful when validating, for example, whether it’s still the same person behind an online avatar.
Now given a paragraph of text sampled from someone’s speech, can you find the person’s most commonly used word?
Input Specification
Each input file contains one test case. For each case, there is one line of text no more than 1048576 characters in length, terminated by a carriage return \n. The input contains at least one alphanumerical character, i.e., one character from the set [0-9 A-Z a-z].
Output Specification
For each test case, print in one line the most commonly occurring word in the input text, followed by a space and the number of times it has occurred in the input. If there are more than one such words, print the lexicographically smallest one. The word should be printed in all lower case. Here a “word” is defined as a continuous sequence of alphanumerical characters separated by non-alphanumerical characters or the line beginning/end.
Note that words are case insensitive.
Sample Input
Can1: “Can a can can a can? It can!”
Sample Output
can 5
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<cctype>
using namespace std;
map<string, int> Map;
string str;
int main(){
	getline(cin, str);
	string tmp;
	bool start=false, end=false;
	for(int i=0;i<str.length();i++){
		if(isalnum(str[i])){
			if(!start) start=true;
			tmp+=tolower(str[i]);
		}else{
			if(!end) end=true;
			if(start&&end){
				start=end=false;
				if(Map.find(tmp)==Map.end()) Map[tmp]=1;
				else Map[tmp]++;
				tmp="";
			}
		}
	}
	if(start){
		if(Map.find(tmp)==Map.end()) Map[tmp]=1;
		else Map[tmp]++;
	}
	int maxN=0;
	for(map<string, int>::iterator it=Map.begin();it!=Map.end();it++){
		if(it->second>maxN){
			maxN=it->second;
			tmp=it->first;
		}
	}
	cout<<tmp<<" "<<maxN<<endl;
	return 0;
}

1072 Gas Station(30)

Description
A gas station has to be built at such a location that the minimum distance between the station and any of the residential housing is as far away as possible. However it must guarantee that all the houses are in its service range.
Now given the map of the city and several candidate locations for the gas station, you are supposed to give the best recommendation. If there are more than one solution, output the one with the smallest average distance to all the houses. If such a solution is still not unique, output the one with the smallest index number.
Input Specification
Each input file contains one test case. For each case, the first line contains 4 positive integers: N $(≤10^{3})$, the total number of houses; M (≤10), the total number of the candidate locations for the gas stations; K $(≤10^{4})$, the number of roads connecting the houses and the gas stations; and $D_{S}$, the maximum service range of the gas station. It is hence assumed that all the houses are numbered from 1 to N, and all the candidate locations are numbered from G1 to GM.
Then K lines follow, each describes a road in the format
P1 P2 Dist
where P1 and P2 are the two ends of a road which can be either house numbers or gas station numbers, and Dist is the integer length of the road.
Output Specification
For each test case, print in the first line the index number of the best location. In the next line, print the minimum and the average distances between the solution and all the houses. The numbers in a line must be separated by a space and be accurate up to 1 decimal place. If the solution does not exist, simply output No Solution.
Sample Input 1
4 3 11 5
1 2 2
1 4 2
1 G1 4
1 G2 3
2 3 2
2 G2 1
3 4 2
3 G3 2
4 G1 3
G2 G1 1
G3 G2 2
Sample Output 1
G1
2.0 3.3(3.2, 事例错了，但是题目OJ判题是对的)
Sample Input 2
2 1 2 10
1 G1 9
2 G1 20
Sample Output 2
No Solution
Program

//注意：各个候选站点也是通往对应居住点的路线！
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
#include<cmath>
using namespace std;
const int MAXV=1011;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int dis;
	Node(){}
	Node(int V,int Dis):v(V),dis(Dis){}
};
int N,M,K,D;
int dist[MAXV];
int vis[MAXV];
vector<Node> Adj[MAXV];
struct Cmp{
	bool operator ()(const int &a,const int &b)const{
		return dist[a]>dist[b];
	}
};
int getID(string str){
	int i=0;
	int n=0;
	while(i<str.length()){
		if(str[i]!='G'){
			n=10*n+str[i]-'0';
		}
		i++;
	}
	if(str[0]=='G') return n+N;
	else return n;
}
void Dijkstra(int s){
	memset(dist, INF, sizeof(dist));
	memset(vis, false, sizeof(vis));
	priority_queue<int, vector<int>, Cmp> pq;
	pq.push(s);
	dist[s]=0;
	int nDone=0;
	while(nDone<N+M&&!pq.empty()){
		int u=pq.top();
		pq.pop();
		if(!vis[u]){
			vis[u]=true;
			nDone++;
		}else continue;
		for(int i=0;i<Adj[u].size();i++){
			int v=Adj[u][i].v;
			int dis=Adj[u][i].dis;
			if(!vis[v]&&dist[u]+dis<dist[v]){
				dist[v]=dist[u]+dis;
				pq.push(v);
			}
		}
	}
}
int main(){
	cin>>N>>M>>K>>D;
	for(int i=0;i<K;i++){
		string a,b;
		int dis;
		cin>>a>>b>>dis;
		int u=getID(a);
		int v=getID(b);
		Adj[u].push_back(Node(v, dis));
		Adj[v].push_back(Node(u, dis));
	}
	int maxMinDis=0, ID=0;
	double avg=0;
	for(int i=N+1;i<=N+M;i++){
		int minDis=INF;
		double avgDis=0;
		Dijkstra(i);
		for(int j=1;j<=N;j++){
			if(dist[j]>D){
				minDis=-1;
				break;
			}
			if(dist[j]<minDis){
				minDis=dist[j];
			}
			avgDis += 1.0 *dist[j];
		}
		avgDis = avgDis * 1.0 / N;
		if(minDis==-1) continue;
		if(minDis>maxMinDis){
			maxMinDis=minDis;
			avg=avgDis;
			ID=i;
		}else if(minDis==maxMinDis&&avg>avgDis){
			ID=i;
			avg=avgDis;
		}
	}
	if(maxMinDis==0){
		cout<<"No Solution"<<endl;
	}else{
		cout<<"G"<<ID-N<<endl;
		if(avg)
		printf("%.1lf %.1lf\n", maxMinDis / 1.0, avg);
	}
	return 0;
}

1073 Scientific Notation(20)

Description
Scientific notation is the way that scientists easily handle very large numbers or very small numbers. The notation matches the regular expression [+-][1-9].[0-9]+E[+-][0-9]+ which means that the integer portion has exactly one digit, there is at least one digit in the fractional portion, and the number and its exponent’s signs are always provided even when they are positive.
Now given a real number A in scientific notation, you are supposed to print A in the conventional notation while keeping all the significant figures.
Input Specification
Each input contains one test case. For each case, there is one line containing the real number A in scientific notation. The number is no more than 9999 bytes in length and the exponent’s absolute value is no more than 9999.
Output Specification
For each test case, print in one line the input number A in the conventional notation, with all the significant figures kept, including trailing zeros.
Sample Input 1
+1.23400E-03
Sample Output 1
0.00123400
Sample Input 2
-1.2E+10
Sample Output 2
-12000000000
Program

#include<iostream>
#include<string>
#include<cmath>
using namespace std;
int main(){
	string str,str1,str2;
	cin>>str;
	char save1,save2;
	str.erase(2,1);//删除小数点 	
	save1=str[0]; //获取符号位
	str.erase(0,1);//删除符号位
	str1=str.substr(0,str.find('E'));//获取E前字符串
	str2=str.substr(str.find('E')+1,str.length()-1-str.find('E'));//获取E后字符串

	save2=str2[0];//获取符号位
	str2.erase(0,1);//删除符号位

	int sum=0;
	for(int i=0;i<str2.length();i++)
	{
		sum = 10 * sum + str2[i] - '0';
	}

	if(save2=='+'){
		if(sum>=str1.length()-1){
			str1.insert(str1.length(),sum-str1.length()+1,'0');
		}
		else{
			str1.insert(sum+1,1,'.');
		}
	}
	else{
		str1.insert(0,sum,'0');
		str1.insert(1,1,'.');
	}
	if(save1=='-')
		str1.insert(0,1,'-');
	cout<<str1;
	return 0;
}

1074 Reversing Linked List(25)

Description
Given a constant K and a singly linked list L, you are supposed to reverse the links of every K elements on L. For example, given L being 1→2→3→4→5→6, if K=3, then you must output 3→2→1→6→5→4; if K=4, you must output 4→3→2→1→5→6.
Input Specification
Each input file contains one test case. For each case, the first line contains the address of the first node, a positive N ($≤10^5$) which is the total number of nodes, and a positive K (≤N) which is the length of the sublist to be reversed. The address of a node is a 5-digit nonnegative integer, and NULL is represented by -1.
Then N lines follow, each describes a node in the format:
Address Data Next
where Address is the position of the node, Data is an integer, and Next is the position of the next node.
Output Specification
For each case, output the resulting ordered linked list. Each node occupies a line, and is printed in the same format as in the input.
Sample Input
00100 6 4
00000 4 99999
00100 1 12309
68237 6 -1
33218 3 00000
99999 5 68237
12309 2 33218
Sample Output
00000 4 33218
33218 3 12309
12309 2 00100
00100 1 99999
99999 5 68237
68237 6 -1
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
struct Node{
	int address;
	int data;
	int next;
};
vector<Node> vec;
vector<Node> order;
vector<Node> result;
int start, n, k;
int main(){
	vec.resize(100001);
	cin>>start>>n>>k;
	int address, data, next;
	for(int i=0;i<n;i++){
		cin>>address>>data>>next;
		vec[address].address = address;
		vec[address].data = data;
		vec[address].next = next;
	}
	next=start;
	while(next!=-1){
		order.push_back(vec[next]);
		next=vec[next].next;
	}
	n = order.size(); //注意！！！存在无效节点！！！！
	int time=0;
	int times=order.size() / k;
	int len=0;
	while(time<times){
		for(int i=(time+1)*k-1;i>=time*k;i--){
			result.push_back(order[i]);
			len++;
		}
		time++;
	}
	while(len<n){
		result.push_back(order[len]);
		len++;
	}
	for(int i=0;i<n-1;i++){
		result[i].next=result[i+1].address;
		printf("%05d %d %05d\n", result[i].address, result[i].data, result[i].next);
	}
	printf("%05d %d -1\n", result[n-1].address, result[n-1].data);
	return 0;
}

1075 PAT Judge(25)

Description
The ranklist of PAT is generated from the status list, which shows the scores of the submissions. This time you are supposed to generate the ranklist for PAT.
Input Specification
Each input file contains one test case. For each case, the first line contains 3 positive integers, N ($≤10^4$), the total number of users, K (≤5), the total number of problems, and M ($≤10^5$), the total number of submissions. It is then assumed that the user id’s are 5-digit numbers from 00001 to N, and the problem id’s are from 1 to K. The next line contains K positive integers p[i] (i=1, …, K), where p[i] corresponds to the full mark of the i-th problem. Then M lines follow, each gives the information of a submission in the following format:
user_id problem_id partial_score_obtained
where partial_score_obtained is either −1 if the submission cannot even pass the compiler, or is an integer in the range [0, p[problem_id]]. All the numbers in a line are separated by a space.
Output Specification
For each test case, you are supposed to output the ranklist in the following format:
`rank user_id total_score s[1] … s[K]``
where rank is calculated according to the total_score, and all the users with the same total_score obtain the same rank; and s[i] is the partial score obtained for the i-th problem. If a user has never submitted a solution for a problem, then “-“ must be printed at the corresponding position. If a user has submitted several solutions to solve one problem, then the highest score will be counted.
The ranklist must be printed in non-decreasing order of the ranks. For those who have the same rank, users must be sorted in nonincreasing order according to the number of perfectly solved problems. And if there is still a tie, then they must be printed in increasing order of their id’s. For those who has never submitted any solution that can pass the compiler, or has never submitted any solution, they must NOT be shown on the ranklist. It is guaranteed that at least one user can be shown on the ranklist.
Sample Input
7 4 20
20 25 25 30
00002 2 12
00007 4 17
00005 1 19
00007 2 25
00005 1 20
00002 2 2
00005 1 15
00001 1 18
00004 3 25
00002 2 25
00005 3 22
00006 4 -1
00001 2 18
00002 1 20
00004 1 15
00002 4 18
00001 3 4
00001 4 2
00005 2 -1
00004 2 0
Sample Output
1 00002 63 20 25 - 18
2 00005 42 20 0 22 -
2 00007 42 - 25 - 17
2 00001 42 18 18 4 2
5 00004 40 15 0 25 -
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<map>
using namespace std;
int n,k,m;
vector<int> problem;
struct User{
	int id;
	int total_score;
	int *score;
	int perNum;
	bool ePass;
	User(){}
	User(int Id){
		id=Id;
		total_score=0;
		score= new int[k];
		ePass=false;
		perNum=0;
		fill(score, score+k, -1);
	}
	bool operator < (const User &tmp) const{
		if(total_score!=tmp.total_score){
			return total_score>tmp.total_score;
		}else if(perNum!=tmp.perNum){
			return perNum>tmp.perNum;
		}else return id<tmp.id;
	}
	void toString(){
		printf("%05d %d", id, total_score);
		for(int i=0;i<k;i++){
			if(score[i]==-1) cout<<" -";
			else cout<<" "<<score[i];
		}
		cout<<endl;
	}
};
map<int, int> idToindex;
vector<User> vec;

void insert(int id, int pi,int score){

	if(idToindex.find(id)==idToindex.end()){
		idToindex[id]=vec.size();
		vec.push_back(User(id));
	}
	int index=idToindex[id];
	if(score!=-1&&!vec[index].ePass)vec[index].ePass=true;
	if(score==-1) score=0;
	if(vec[index].score[pi]<score){
		if(score==problem[pi]){
			vec[index].perNum++;
		}
		if(vec[index].score[pi]!=-1) vec[index].total_score+=score-vec[index].score[pi];
		else vec[index].total_score+=score;
		vec[index].score[pi]=score;
	}
}
int main(){
	cin>>n>>k>>m;
	problem.resize(k);
	for(int i=0;i<k;i++){
		cin>>problem[i];
	}
	for(int i=0;i<m;i++){
		int id, pi,score;
		cin>>id>>pi>>score;
		insert(id,pi-1,score);
	}
	sort(vec.begin(),vec.end());

	int rank=1;
	for(int i=0;i<vec.size();i++){
		if(i!=0&&vec[i].total_score!=vec[i-1].total_score){
			rank=i+1;
		}
		if(vec[i].ePass){
			cout<<rank<<" ";
			vec[i].toString();
		}
	}
	return 0;
}

1076 Forwards on Weibo(30)

Description
Weibo is known as the Chinese version of Twitter. One user on Weibo may have many followers, and may follow many other users as well. Hence a social network is formed with followers relations. When a user makes a post on Weibo, all his/her followers can view and forward his/her post, which can then be forwarded again by their followers. Now given a social network, you are supposed to calculate the maximum potential amount of forwards for any specific user, assuming that only L levels of indirect followers are counted.
Input Specification
Each input file contains one test case. For each case, the first line contains 2 positive integers: N (≤1000), the number of users; and L (≤6), the number of levels of indirect followers that are counted. Hence it is assumed that all the users are numbered from 1 to N. Then N lines follow, each in the format:
M[i] user_list[i]
where M[i] (≤100) is the total number of people that user[i] follows; and user_list[i] is a list of the M[i] users that followed by user[i]. It is guaranteed that no one can follow oneself. All the numbers are separated by a space.
Then finally a positive K is given, followed by K UserID’s for query.
Output Specification
For each UserID, you are supposed to print in one line the maximum potential amount of forwards this user can trigger, assuming that everyone who can view the initial post will forward it once, and that only L levels of indirect followers are counted.
Sample Input
7 3
3 2 3 4
0
2 5 6
2 3 1
2 3 4
1 4
1 5
2 2 6
Sample Output
4
5
Program

#include<iostream>
#include<queue>
#include<vector>
#include<cstring>
using namespace std;

const int MAXV=1001;
struct Node{
	int vertex;
	int layer;
	Node(){}
	Node(int v,int l):vertex(v),layer(l){}
};

int N,L;
vector<Node> Adj[MAXV];
bool bInq[MAXV];
int BFS(int u){
	memset(bInq,false,sizeof(bInq));
	queue<Node> q;
	bInq[u]=true;
	q.push(Node(u,0));
	int num=0;
	while(!q.empty()){
		Node tmp=q.front();
		q.pop();
		int u=tmp.vertex;
		for(int i=0;i<Adj[u].size();i++){
			Node v=Adj[u][i];
			v.layer=tmp.layer+1;
			if(!bInq[v.vertex]&&v.layer<=L){
				num++;
				q.push(v);
				bInq[v.vertex]=true;
			}
		}
	}
	return num;
}
int main(){
	cin>>N>>L;
	for(int i=1;i<=N;i++){
		int m;
		cin>>m;
		for(int j=0;j<m;j++){
			int v;
			cin>>v;
			Adj[v].push_back(Node(i,1));
		}
	}
	int m;
	cin>>m;
	for(int j=0;j<m;j++){
		int v;
		cin>>v;
		cout<<BFS(v)<<endl;
	}
	return 0;
}

1077 Kuchiguse(20)

Description
The Japanese language is notorious for its sentence ending particles. Personal preference of such particles can be considered as a reflection of the speaker’s personality. Such a preference is called “Kuchiguse” and is often exaggerated artistically in Anime and Manga. For example, the artificial sentence ending particle “nyan~” is often used as a stereotype for characters with a cat-like personality:

• Itai nyan~ (It hurts, nyan~)
• Ninjin wa iyada nyan~ (I hate carrots, nyan~)
  Now given a few lines spoken by the same character, can you find her Kuchiguse?

Input Specification
Each input file contains one test case. For each case, the first line is an integer N (2≤N≤100). Following are N file lines of 0256 (inclusive) characters in length, each representing a character’s spoken line. The spoken lines are case sensitive.
Output Specification
For each test case, print in one line the kuchiguse of the character, i.e., the longest common suffix of all N lines. If there is no such suffix, write nai.
Sample Input 1
3
Itai nyan
Ninjin wa iyadanyan~
uhhh nyan~
Sample Output 1
nyan~
Sample Input 2
3
Itai!
Ninjinnwaiyada T_T
T_T
Sample Output 2
nai
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
using namespace std;
int N;
vector<string> vec;
int main(){
	cin>>N;
	getchar();
	vec.clear();
	vec.resize(N);
	int minLen=256;
	for(int i=0;i<N;i++){
		getline(cin, vec[i]);
		reverse(vec[i].begin(),vec[i].end());
		minLen=min(minLen,(int)vec[i].length());
	}
	int maxIndex=-1;
	for(int i=0;i<minLen;i++){
		char ch=vec[0][i];
		int j;
		for(j=1;j<N;j++){
			if(ch!=vec[j][i]) break;
		}
		if(j==N) maxIndex=i;
		else break;
	}
	if(maxIndex==-1) cout<<"nai"<<endl;
	else{
		string str=vec[0].substr(0, maxIndex+1);
		reverse(str.begin(),str.end());
		cout<<str<<endl;
	}
	return 0;
}

1078 Hashing(25)

Description
The task of this problem is simple: insert a sequence of distinct positive integers into a hash table, and output the positions of the input numbers. The hash function is defined to be H(key)=key%TSize where TSize is the maximum size of the hash table. Quadratic probing (with positive increments only) is used to solve the collisions.
Note that the table size is better to be prime. If the maximum size given by the user is not prime, you must re-define the table size to be the smallest prime number which is larger than the size given by the user.
Input Specification
Each input file contains one test case. For each case, the first line contains two positive numbers: MSize ($≤10^{4}$) and N (≤MSize) which are the user-defined table size and the number of input numbers, respectively. Then N distinct positive integers are given in the next line. All the numbers in a line are separated by a space.
Output Specification
For each test case, print the corresponding positions (index starts from 0) of the input numbers in one line. All the numbers in a line are separated by a space, and there must be no extra space at the end of the line. In case it is impossible to insert the number, print “-“ instead.
Sample Input
4 4
10 6 4 15
Sample Output
0 1 4 -
Program

#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN=11111;
bool vis[MAXN]={false};
int n,m;
bool isPrime(int x){
	if(x<=1) return false;
	for(int i=2;i*i<=x;i++){
		if(x%i==0) return false;
	}
	return true;
}
int main(){
	cin>>m>>n;
	while(!isPrime(m)) m++;
	for(int i=0;i<n;i++){
		int x;
		cin>>x;
		if(i!=0) cout<<" ";
		if(!vis[x%m]){
			cout<<x%m;
			vis[x%m]=true;
		}else{
			int step=1;
			while(step<m&&vis[(x+step*step)%m]) step++;
			if(step==m) cout<<"-";
			else{
				cout<<(x+step*step)%m;
				vis[(x+step*step)%m]=true;
			}
		}
	}
	return 0;
}

1079 Total Sales of Supply Chain(25)

Description
A supply chain is a network of retailers（零售商）, distributors（经销商）, and suppliers（供应商）– everyone involved in moving a product from supplier to customer.
Starting from one root supplier, everyone on the chain buys products from one’s supplier in a price P and sell or distribute them in a price that is r% higher than P. Only the retailers will face the customers. It is assumed that each member in the supply chain has exactly one supplier except the root supplier, and there is no supply cycle.
Now given a supply chain, you are supposed to tell the total sales from all the retailers.
Input Specification
Each input file contains one test case. For each case, the first line contains three positive numbers: N ($≤10^{5}$), the total number of the members in the supply chain (and hence their ID’s are numbered from 0 to N−1, and the root supplier’s ID is 0); P, the unit price given by the root supplier; and r, the percentage rate of price increment for each distributor or retailer. Then N lines follow, each describes a distributor or retailer in the following format:
`Ki ID[1] ID[2] … ID[Ki]``
where in the i-th line, Ki is the total number of distributors or retailers who receive products from supplier i, and is then followed by the ID’s of these distributors or retailers. Kj being 0 means that the j-th member is a retailer, then instead the total amount of the product will be given after Kj. All the numbers in a line are separated by a space.
Output Specification
For each test case, print in one line the total sales we can expect from all the retailers, accurate up to 1 decimal place. It is guaranteed that the number will not exceed $10^{10}$.
Sample Input
10 1.80 1.00
3 2 3 5
1 9
1 4
1 7
0 7
2 6 1
1 8
0 9
0 4
0 3
Sample Output
42.4
Program

#include<iostream>
#include<algorithm>
#include<vector>
#include<cmath>
#include<cstring>
using namespace std;
struct Node{
	int data;
	vector<int> child;
};
vector<Node> tree;
int N;
double P,r;
double sum=0;
void preOrder(int root, int depth){
	sum+=P*tree[root].data*pow(1+r/100, depth);
	for(int i=0;i<tree[root].child.size();i++){
		int childIdx=tree[root].child[i];
		preOrder(childIdx, depth+1);
	}
}
int main(){
	cin>>N>>P>>r;
	tree.resize(N);
	for(int i=0;i<N;i++){
		int K, tmp;
		cin>>K;
		if(K==0){
			cin>>tmp;
			tree[i].data=tmp;
		}else{
			tree[i].data=0;
			for(int j=0;j<K;j++){
				cin>>tmp;
				tree[i].child.push_back(tmp);
			}
		}
	}
	preOrder(0, 0);
	printf("%.1f\n", sum);
	return 0;
}

1080 Graduate Admission(30)

Description
It is said that in 2011, there are about 100 graduate schools ready to proceed over 40,000 applications in Zhejiang Province. It would help a lot if you could write a program to automate the admission Program.
Each applicant will have to provide two grades: the national entrance exam grade $G_E$, and the interview grade $G_I$. The final grade of an applicant is $(G_​E+G_I)/2$. The admission rules are:

• The applicants are ranked according to their final grades, and will be admitted one by one from the top of the rank list.
• If there is a tied final grade, the applicants will be ranked according to their national entrance exam grade $G_​E$. If still tied, their ranks must be the same.
• Each applicant may have K choices and the admission will be done according to his/her choices: if according to the rank list, it is one’s turn to be admitted; and if the quota of one’s most preferred shcool is not exceeded, then one will be admitted to this school, or one’s other choices will be considered one by one in order. If one gets rejected by all of preferred schools, then this unfortunate applicant will be rejected.
• If there is a tied rank, and if the corresponding applicants are applying to the same school, then that school must admit all the applicants with the same rank, even if its quota will be exceeded.

Input Specification
Each input file contains one test case.
Each case starts with a line containing three positive integers: N (≤40,000), the total number of applicants; M (≤100), the total number of graduate schools; and K (≤5), the number of choices an applicant may have.
In the next line, separated by a space, there are M positive integers. The i-th integer is the quota of the i-th graduate school respectively.
Then N lines follow, each contains 2+K integers separated by a space. The first 2 integers are the applicant’s $G_E$ and $G_I$
​​ , respectively. The next K integers represent the preferred schools. For the sake of simplicity, we assume that the schools are numbered from 0 to M−1, and the applicants are numbered from 0 to N−1.
Output Specification
For each test case you should output the admission results for all the graduate schools. The results of each school must occupy a line, which contains the applicants’ numbers that school admits. The numbers must be in increasing order and be separated by a space. There must be no extra space at the end of each line. If no applicant is admitted by a school, you must output an empty line correspondingly.
Sample Input
11 6 3
2 1 2 2 2 3
100 100 0 1 2
60 60 2 3 5
100 90 0 3 4
90 100 1 2 0
90 90 5 1 3
80 90 1 0 2
80 80 0 1 2
80 80 0 1 2
80 70 1 3 2
70 80 1 2 3
100 100 0 2 4
Sample Output

0 10
3
5 6 7
2 8

1 4

Program

#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
struct Student{
	int ge, gi;
	int rank;
	int id;
	int total;
	int choices[5];
	Student(){}
	bool operator < (const Student &tmp){
		if(total!=tmp.total) return total>tmp.total;
		else return ge>tmp.ge;
	}
};
struct School{
	int quota;
	int admit;
	Student lastAdmit;
	vector<int> ids;
};
vector<School> schools;
vector<Student> students;
int n,k,m;
int main(){
	cin>>n>>m>>k;
	schools.resize(m);
	Student flag;
	flag.total=-1;
	for(int i=0;i<m;i++){
		cin>>schools[i].quota;
		schools[i].admit=0;
		schools[i].lastAdmit=flag;
	}
	students.resize(n);
	for(int i=0;i<n;i++){
		cin>>students[i].ge>>students[i].gi;
		students[i].total=students[i].ge+students[i].gi;
		for(int j=0;j<k;j++){
			cin>>students[i].choices[j];
		}
		students[i].rank=0;
		students[i].id=i;
	}
	sort(students.begin(), students.end());
	int rank=0;
	for(int i=0;i<students.size();i++){
		if(i!=0&&(students[i].total!=students[i-1].total
			||students[i].ge!=students[i-1].ge)){
			rank++;
		}
		students[i].rank=rank;
	}
	for(int i=0;i<students.size();i++){
		for(int j=0;j<k;j++){
			int index=students[i].choices[j];
			if(schools[index].admit<schools[index].quota){
				schools[index].admit++;
				schools[index].lastAdmit=students[i];
				schools[index].ids.push_back(students[i].id);
				break;
			}else if(students[i].rank==schools[index].lastAdmit.rank){
				schools[index].admit++;
				schools[index].ids.push_back(students[i].id);
				break;
			}
		}
	}
	for(int i=0;i<m;i++){
		sort(schools[i].ids.begin(), schools[i].ids.end());
		for(int j=0;j<schools[i].ids.size();j++){
			if(j!=0) cout<<" ";
			cout<<schools[i].ids[j];
		}
		cout<<endl;
	}
	return 0;
}

1081 Rational Sum(20)

Description
Given N rational numbers in the form numerator/denominator, you are supposed to calculate their sum.
Input Specification
Each input file contains one test case. Each case starts with a positive integer N (≤100), followed in the next line N rational numbers a1/b1 a2/b2 … where all the numerators and denominators are in the range of long int. If there is a negative number, then the sign must appear in front of the numerator.
Output Specification
For each test case, output the sum in the simplest form integer numerator/denominator where integer is the integer part of the sum, numerator < denominator, and the numerator and the denominator have no common factor. You must output only the fractional part if the integer part is 0.
Sample Input 1
5
2/5 4/15 1/30 -2/60 8/3
Sample Output 1
3 1/3
Sample Input 2
2
4/3 2/3
Sample Output 2
2
Sample Input 3
3
1/3 -1/6 1/8
Sample Output 3
7/24
Program

#include<iostream>
#include<cmath>
#include<queue>
using namespace std;
struct Fraction{
	long long up;
	long long down;
	Fraction(){}
	Fraction(long long Up, long long Down):up(Up),down(Down){}
};
long long gcd(long long x, long long y){
	if(y==0) return x;
	else return gcd(y, x%y);
}
Fraction reduction(Fraction fraction){
	if(fraction.down<0){
		fraction.up=-fraction.up;
		fraction.down=-fraction.down;
	}
	if(fraction.up==0){
		fraction.down=1;
	}else{
		long long x=gcd(abs(fraction.up),abs(fraction.down));
		fraction.up/=x;
		fraction.down/=x;
	}
	return fraction;
}
Fraction addition(Fraction f1, Fraction f2){
	Fraction result;
	result.up=f1.up*f2.down+f1.down*f2.up;
	result.down=f1.down*f2.down;
	return reduction(result);
}
int n;
queue<Fraction> q;
int main(){
	cin>>n;
	for(int i=0;i<n;i++){
		long long up,down;
		scanf("%lld/%lld",&up,&down);
		q.push(reduction(Fraction(up,down)));
	}
	while(q.size()!=1){
		Fraction f1=q.front();
		q.pop();
		Fraction f2=q.front();
		q.pop();
		Fraction result=addition(f1,f2);
		q.push(result);
	}
	Fraction result=q.front();
	q.pop();
	if(result.up==0) cout<<0<<endl;
	else{
		long long integer=result.up/result.down;
		result.up=result.up%result.down;
		result=reduction(result);
		if(result.up==0) printf("%lld\n", integer);
		else if(integer!=0)printf("%lld %lld/%lld\n", integer, result.up,result.down);
		else printf("%lld/%lld\n", result.up,result.down);
	}
	return 0;
}

1082 Read Number in Chinese(25)

Description
Given an integer with no more than 9 digits, you are supposed to read it in the traditional Chinese way. Output Fu first if it is negative. For example, -123456789 is read as Fu yi Yi er Qian san Bai si Shi wu Wan liu Qian qi Bai ba Shi jiu. Note: zero (ling) must be handled correctly according to the Chinese tradition. For example, 100800 is yi Shi Wan ling ba Bai.
Input Specification
Each input file contains one test case, which gives an integer with no more than 9 digits.
Output Specification
For each test case, print in a line the Chinese way of reading the number. The characters are separated by a space and there must be no extra space at the end of the line.
Sample Input 1
-123456789
Sample Output 1
Fu yi Yi er Qian san Bai si Shi wu Wan liu Qian qi Bai ba Shi jiu
Sample Input 2
100800
Sample Output 2
yi Shi Wan ling ba Bai
Program

//注意样例
//0     ling
//8     ba
//808080808   ba Yi ling ba Bai ling ba Wan ling ba Bai ling ba
//-880808080  Fu ba Yi ba Qian ling ba Shi Wan ba Qian ling ba Shi
//800000008   ba Yi ling ba
//800000000   ba Yi
//80000008    ba Qian Wan ling ba
//80008000    ba Qian Wan ba Qian
//80000000    ba Qian Wan
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
const string UNITS[]={"","Shi","Bai","Qian","Wan","Yi"};
const string NUM[]={"ling", "yi", "er", "san", "si", "wu", "liu", "qi", "ba", "jiu"};
string str;
vector<string> vec;
int main(){
	cin>>str;
	int len=str.length();
	int left=0, right=len-1;
	if(str[0]=='-'){
		vec.push_back("Fu");
		left++;
	}
	int multi=0;
	while(left+4<=right){
		right-=4;
		multi++;
	}
	int start=left;
	if(str[left]=='0'){
		cout<<"ling"<<endl;
		return 0;
	}
	while(left<len){
		while(left<=right){
			if(str[left]!='0'){
				if(left!=start&&right-left!=3){
					if(str[left-1]=='0') vec.push_back("ling");
				}
				vec.push_back(NUM[str[left]-'0']);
				if(right-left!=0){
					vec.push_back(UNITS[right-left]);
				}
			}
			if(left==right&&left!=len-1){
				if(vec[vec.size()-1]!="Yi"){
					vec.push_back(UNITS[multi+3]);
				}
			}
			left++;
		}
		right+=4;
		multi--;
	}
	for(vector<string>::iterator it=vec.begin();it!=vec.end();it++){
		if(it!=vec.begin()) cout<<" ";
		cout<<*it;
	}
	cout<<endl;
	return 0;
}

1083 List Grades(25)

Description
Given a list of N student records with name, ID and grade. You are supposed to sort the records with respect to the grade in non-increasing order, and output those student records of which the grades are in a given interval.
Input Specification
Each input file contains one test case. Each case is given in the following format:
N
name[1] ID[1] grade[1]
name[2] ID[2] grade[2]
… …
name[N] ID[N] grade[N]
grade1 grade2
where name[i] and ID[i] are strings of no more than 10 characters with no space, grade[i] is an integer in [0, 100], grade1 and grade2 are the boundaries of the grade’s interval. It is guaranteed that all the grades are distinct.
Output Specification
For each test case you should output the student records of which the grades are in the given interval [grade1, grade2] and are in non-increasing order. Each student record occupies a line with the student’s name and ID, separated by one space. If there is no student’s grade in that interval, output NONE instead.
Sample Input 1
4
Tom CS000001 59
Joe Math990112 89
Mike CS991301 100
Mary EE990830 95
60 100
Sample Output 1
Mike CS991301
Mary EE990830
Joe Math990112
Sample Input 2
2
Jean AA980920 60
Ann CS01 80
90 95
Sample Output 2
NONE
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
int n, l, r;
struct Node{
	string name;
	string id;
	int score;
	Node(){}
	Node(string Name, string Id, int Score):name(Name),id(Id),score(Score){}
	bool operator < (const Node &tmp) const{
		return score>tmp.score;
	}
};
vector<Node> vec;
int main(){
	cin>>n;
	vec.resize(n);
	for(int i=0;i<n;i++){
		cin>>vec[i].name>>vec[i].id>>vec[i].score;
	}
	sort(vec.begin(), vec.end());
	cin>>l>>r;
	bool isPrint=false;
	for(int i=0;i<vec.size();i++){
		if(vec[i].score>=l&&vec[i].score<=r){
			cout<<vec[i].name<<" "<<vec[i].id<<endl;
			isPrint=true;
		}
	}
	if(!isPrint) cout<<"NONE"<<endl;
	return 0;
}

1084 Broken Keyboard(20)

Description
On a broken keyboard, some of the keys are worn out. So when you type some sentences, the characters corresponding to those keys will not appear on screen.
Now given a string that you are supposed to type, and the string that you actually type out, please list those keys which are for sure worn out.
Input Specification
Each input file contains one test case. For each case, the 1st line contains the original string, and the 2nd line contains the typed-out string. Each string contains no more than 80 characters which are either English letters [A-Z] (case insensitive), digital numbers [0-9], or _ (representing the space). It is guaranteed that both strings are non-empty.
Output Specification
For each test case, print in one line the keys that are worn out, in the order of being detected. The English letters must be capitalized. Each worn out key must be printed once only. It is guaranteed that there is at least one worn out key.
Sample Input

7_This_is_a_test
_hs_s_a_es

Sample Output

7TI

Program

#include<iostream>
#include<cstring>
#include<set>
#include<cctype>
using namespace std;
set<char> s, isPrint;
string s1, s2;
int main(){
	getline(cin, s1);
	getline(cin, s2);
	for(int i=0;i<s2.length();i++){
		if(islower(s2[i])) s2[i]=toupper(s2[i]);
		if(s.find(s2[i])==s.end()){
			s.insert(s2[i]);
		}
	}
	for(int i=0;i<s1.length();i++){
		if(islower(s1[i])) s1[i]=toupper(s1[i]);
		if(s.find(s1[i])==s.end()&&isPrint.find(s1[i])==isPrint.end()){
			cout<<s1[i];
			isPrint.insert(s1[i]);
		}
	}
	cout<<endl;
	return 0;
}

1085 Perfect Sequence(25)

Description
Given a sequence of positive integers and another positive integer p. The sequence is said to be a perfect sequence if M≤m×p where M and m are the maximum and minimum numbers in the sequence, respectively.
Now given a sequence and a parameter p, you are supposed to find from the sequence as many numbers as possible to form a perfect subsequence.
Input Specification
Each input file contains one test case. For each case, the first line contains two positive integers N and p, where N ($≤10^5$) is the number of integers in the sequence, and p$(\leq 10^​9)$ is the parameter. In the second line there are N positive integers, each is no greater than $10​^9$.
Output Specification
For each test case, print in one line the maximum number of integers that can be chosen to form a perfect subsequence.
Sample Input
10 8
2 3 20 4 5 1 6 7 8 9
Sample Output
8
Program

#include<iostream>
#include<set>
#include<vector>
#include<algorithm>
using namespace std;
int main() {
	long n, p;
	vector<long>b;
	long a[100010];
	scanf("%ld %ld", &n, &p);
	for (long i = 0; i < n; i++){
		scanf("%ld", &a[i]);
	}

	sort(a, a + n);

	int Maxlen = 0;
	for (int i = 0; i < n; i++){
		for (int j = i + Maxlen; j < n; j++){
			if (a[j] > a[i] * p)break;
			Maxlen = max(Maxlen, j - i + 1);
		}
	}
	printf("%ld\n", Maxlen);
	return 0;
}

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
vector<int> vec;
int n,p;
int binarySearch(int i, long long x){
	if(vec[n-1]<=x) return n;
	int l=i, r=n-1;
	while(l<r){
		int mid=(l+r)/2;
		if(vec[mid]<=x) l=mid+1;
		else r=mid;
	}
	return l;
}
int main(){
	cin>>n>>p;
	vec.resize(n);
	for(int i=0;i<n;i++) cin>>vec[i];
	sort(vec.begin(),vec.end());
	int maxLen=0;
	for(int i=0;i<n;i++){
		int j=binarySearch(i, (long long)vec[i]*p);
		maxLen=max(maxLen, j-i);
	}
	cout<<maxLen<<endl;
	return 0;
}

#include<iostream>
#include<set>
#include<vector>
#include<algorithm>
using namespace std;
int main() {
	long n, p;
	vector<long>b;
	long a[100010];
	scanf("%ld %ld", &n, &p);
	for (long i = 0; i < n; i++){
		scanf("%ld", &a[i]);
	}

	sort(a, a + n);

	int Maxlen = 0;
	for (int i = 0; i < n; i++){
		int j=upper_bound(a+i,a+n,(long long)a[i]*p)-a;
		Maxlen=max(Maxlen, j-i);
	}
	printf("%ld\n", Maxlen);
	return 0;
}

1086 Tree Traversals Again(25)

Description
An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.

Figure 1
Input Specification
Each input file contains one test case. For each case, the first line contains a positive integer N (≤30) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2N lines follow, each describes a stack operation in the format: “Push X” where X is the index of the node being pushed onto the stack; or “Pop” meaning to pop one node from the stack.
Output Specification
For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.
Sample Input
6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop
Sample Output
3 4 2 6 5 1
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<stack>
#include<vector>
using namespace std;
struct Node{
	int data;
	Node *lchild, *rchild;
};
vector<int> preOrder, inOrder;
int N;
stack<int> stk;
bool isFirst=true;
Node* create(int preL,int preR, int inL,int inR){
	if(preL>preR||inL>inR) return NULL;
	Node* root=new Node;
	root->data=preOrder[preL];
	int pos;
	for(pos=inL;pos<=inR;pos++){
		if(preOrder[preL]==inOrder[pos]) break;
	}
	int leftNum=pos-inL;
	root->lchild=create(preL+1, preL+leftNum,inL,pos-1);
	root->rchild=create(preL+leftNum+1,preR,pos+1,inR);
	return root;
}
void postOrder(Node* root){
	if(root!=NULL){
		postOrder(root->lchild);
		postOrder(root->rchild);
		if(isFirst) isFirst=false;
		else cout<<" ";
		cout<<root->data;
	}
}
int main(){
	cin>>N;
	for(int i=0;i<2*N;i++){
		string str;
		cin>>str;
		if(str=="Push"){
			int tmp;
			cin>>tmp;
			stk.push(tmp);
			preOrder.push_back(tmp);
		}else{
			int top=stk.top();
			stk.pop();
			inOrder.push_back(top);
		}
	}
	postOrder(create(0, N-1, 0, N-1));
	cout<<endl;
	return 0;
}

1087 All Roads Lead to Rome(30)

Description
Indeed there are many different tourist routes from our city to Rome. You are supposed to find your clients the route with the least cost while gaining the most happiness.
Input Specification
Each input file contains one test case. For each case, the first line contains 2 positive integers N (2≤N≤200), the number of cities, and K, the total number of routes between pairs of cities; followed by the name of the starting city. The next N−1 lines each gives the name of a city and an integer that represents the happiness one can gain from that city, except the starting city. Then K lines follow, each describes a route between two cities in the format City1 City2 Cost. Here the name of a city is a string of 3 capital English letters, and the destination is always ROM which represents Rome.
Output Specification
For each test case, we are supposed to find the route with the least cost. If such a route is not unique, the one with the maximum happiness will be recommanded. If such a route is still not unique, then we output the one with the maximum average happiness – it is guaranteed by the judge that such a solution exists and is unique.
Hence in the first line of output, you must print 4 numbers: the number of different routes with the least cost, the cost, the happiness, and the average happiness (take the integer part only) of the recommanded route. Then in the next line, you are supposed to print the route in the format City1->City2->...->ROM.
Sample Input
6 7 HZH
ROM 100
PKN 40
GDN 55
PRS 95
BLN 80
ROM GDN 1
BLN ROM 1
HZH PKN 1
PRS ROM 2
BLN HZH 2
PKN GDN 1
HZH PRS 1
Sample Output
3 3 195 97
HZH->PRS->ROM
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
#include<map>
using namespace std;
const int MAXV=201;
const int INF=0x3f3f3f3f;
struct Node{
	int v;
	int cos;
	Node(){}
	Node(int V,int Cos):v(V),cos(Cos){}
};
int N,K, Index=1, dst;
string src;
vector<Node> Adj[MAXV];
bool vis[MAXV];
int cost[MAXV];
int happy[MAXV];
int hap[MAXV];
int num[MAXV];
int pre[MAXV];
int nS[MAXV];
struct Cmp{
	bool operator ()(const int &a, const int &b)const{
		return cost[a]>cost[b];
	}
};
map<string, int> sToi;
map<int, string> iTos;
int getNumber(string str){
	if(sToi.find(str)==sToi.end()){
		sToi[str]=Index;
		iTos[Index]=str;
		if(str=="ROM") dst=Index;
		Index++;
	}
	return sToi[str];
}
void Dijkstra(int s){
	memset(cost, INF, sizeof(cost));
	memset(vis, false, sizeof(vis));
	memset(hap, 0,sizeof(hap));
	memset(num, 0, sizeof(num));
	memset(nS, 0, sizeof(nS));
	cost[s]=0;
	hap[s]=0;
	num[s]=1;
	nS[s]=0;
	priority_queue<int, vector<int>, Cmp> pq;
	pq.push(s);
	int nDone=0;
	while(nDone<N&&!pq.empty()){
		int u=pq.top();
		pq.pop();
		if(!vis[u]){
			vis[u]=true;
			nDone++;
			if(u==dst) break;
		}else continue;
		for(int i=0;i<Adj[u].size();i++){
			int v=Adj[u][i].v;
			int cos=Adj[u][i].cos;
			if(!vis[v]){
				if(cost[u]+cos<cost[v]){
					cost[v]=cost[u]+cos;
					num[v]=num[u];
					pre[v]=u;
					hap[v]=hap[u]+happy[v];
					nS[v]=nS[u]+1;
					pq.push(v);
				}else if(cost[u]+cos==cost[v]){
					num[v]+=num[u];
					if(hap[u]+happy[v]>hap[v]){
						pre[v]=u;
						hap[v]=hap[u]+happy[v];
						nS[v]=nS[u]+1;
					}else if(hap[u]+happy[v]==hap[v]&&((1.0*hap[v]/(nS[u]+1))>(1.0*hap[v]/nS[v]))){
						pre[v]=u;
						nS[v]=nS[u]+1;
					}

				}
			}
		}
	}
}
void DFS(int u){
	if(u==pre[u]){
		cout<<iTos[u];
		return;
	}
	DFS(pre[u]);
	cout<<"->"<<iTos[u];
}
int main(){
	cin>>N>>K>>src;
	sToi[src]=0;
	iTos[0]=src;
	pre[0]=0;
	for(int i=0;i<N-1;i++){
		string str;
		int hap;
		cin>>str>>hap;
		int idx=getNumber(str);
		happy[idx]=hap;
		pre[i+1]=i+1;
	}
	for(int i=0;i<K;i++){
		string a,b;
		int c;
		cin>>a>>b>>c;
		int u=getNumber(a);
		int v=getNumber(b);
		Adj[u].push_back(Node(v, c));
		Adj[v].push_back(Node(u, c));
	}
	Dijkstra(0);
	cout<<num[dst]<<" "<<cost[dst]<<" "<<hap[dst]<<" "<<hap[dst]/nS[dst]<<endl;
	DFS(dst);
	cout<<endl;
	return 0;
}

1088 Rational Arithmetic(20)

Description
For two rational numbers, your task is to implement the basic arithmetics, that is, to calculate their sum, difference, product and quotient.
Input Specification
Each input file contains one test case, which gives in one line the two rational numbers in the format a1/b1 a2/b2. The numerators and the denominators are all in the range of long int. If there is a negative sign, it must appear only in front of the numerator. The denominators are guaranteed to be non-zero numbers.
Output Specification
For each test case, print in 4 lines the sum, difference, product and quotient of the two rational numbers, respectively. The format of each line is number1 operator number2 = result. Notice that all the rational numbers must be in their simplest form k a/b, where k is the integer part, and a/b is the simplest fraction part. If the number is negative, it must be included in a pair of parentheses. If the denominator in the division is zero, output Inf as the result. It is guaranteed that all the output integers are in the range of long int.
Sample Input 1
2/3 -4/2
Sample Output 1
2/3 + (-2) = (-1 1/3)
2/3 - (-2) = 2 2/3
2/3 * (-2) = (-1 1/3)
2/3 / (-2) = (-1/3)
Sample Input 2
5/3 0/6
Sample Output 2
1 2/3 + 0 = 1 2/3
1 2/3 - 0 = 1 2/3
1 2/3 * 0 = 0
1 2/3 / 0 = Inf
Program

#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long LL;
const char chs[]={'+','-','*','/'};
struct Fraction{
	LL up;
	LL down;
	Fraction(){}
	Fraction(LL Up, LL Down):up(Up),down(Down){}
}a,b;
LL gcd(LL x, LL y){
	return (y==0)?x:gcd(y,x%y);
}
Fraction reduction(Fraction fraction){
	if(fraction.down<0){
		fraction.up=-fraction.up;
		fraction.down=-fraction.down;
	}
	if(fraction.up==0){
		fraction.down=1;
	}else{
		LL gc=gcd(abs(fraction.up),abs(fraction.down));
		fraction.up/=gc;
		fraction.down/=gc;
	}
	return fraction;
}
Fraction add(Fraction f1, Fraction f2){
	Fraction result;
	result.up=f1.up*f2.down+f1.down*f2.up;
	result.down=f1.down*f2.down;
	return reduction(result);
}
Fraction diff(Fraction f1, Fraction f2){
	Fraction result;
	result.up=f1.up*f2.down-f2.up*f1.down;
	result.down=f1.down*f2.down;
	return reduction(result);
}
Fraction multi(Fraction f1, Fraction f2){
	Fraction result;
	result.up=f1.up*f2.up;
	result.down=f1.down*f2.down;
	return reduction(result);
}
Fraction quot(Fraction f1, Fraction f2){
	Fraction result;
	if(f2.up==0){
		result.up=0;
		result.down=-1;
	}else{
		result.up=f1.up*f2.down;
		result.down=f1.down*f2.up;
		result=reduction(result);
	}
	return result;
}
void print(Fraction fraction){
	if(fraction.down==-1){
		cout<<"Inf";
		return;
	}
	if(abs(fraction.up)>=abs(fraction.down)){
		LL integer = fraction.up/fraction.down;
		fraction.up %= fraction.down;
		fraction.up=abs(fraction.up);
		if(integer<0||fraction.up<0){
			cout<<"(";
		}
		if(integer!=0) cout<<integer;
		if(integer!=0&&fraction.up!=0) cout<<" ";
		if(fraction.up!=0) cout<<fraction.up<<"/"<<fraction.down;
		else if(integer==0) cout<<0;
		if(integer<0||fraction.up<0){
			cout<<")";
		}
	}else{
		if(fraction.up<0){
			cout<<"(";
		}
		if(fraction.up!=0) cout<<fraction.up<<"/"<<fraction.down;
		else cout<<0;
		if(fraction.up<0){
			cout<<")";
		}
	}
}
void output(Fraction a, Fraction b, Fraction c, int type){
	print(a);
	cout<<" "<<chs[type]<<" ";
	print(b);
	cout<<" = ";
	print(c);
	cout<<endl;
}
int main(){
	scanf("%lld/%lld %lld/%lld", &a.up,&a.down,&b.up,&b.down);
	a=reduction(a);
	b=reduction(b);
	Fraction fs[4];
	fs[0]=add(a,b);
	fs[1]=diff(a,b);
	fs[2]=multi(a,b);
	fs[3]=quot(a,b);
	for(int i=0;i<4;i++){
		output(a,b,fs[i],i);
	}
	return 0;
}

1089 Insert or Merge(25)

Description
According to Wikipedia:
Insertion sort iterates, consuming one input element each repetition, and growing a sorted output list. Each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list, and inserts it there. It repeats until no input elements remain.
Merge sort works as follows: Divide the unsorted list into N sublists, each containing 1 element (a list of 1 element is considered sorted). Then repeatedly merge two adjacent sublists to produce new sorted sublists until there is only 1 sublist remaining.
Now given the initial sequence of integers, together with a sequence which is a result of several iterations of some sorting method, can you tell which sorting method we are using?
Input Specification
Each input file contains one test case. For each case, the first line gives a positive integer N (≤100). Then in the next line, N integers are given as the initial sequence. The last line contains the partially sorted sequence of the N numbers. It is assumed that the target sequence is always ascending. All the numbers in a line are separated by a space.
Output Specification
For each test case, print in the first line either “Insertion Sort” or “Merge Sort” to indicate the method used to obtain the partial result. Then run this method for one more iteration and output in the second line the resuling sequence. It is guaranteed that the answer is unique for each test case. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line.
Sample Input 1
10
3 1 2 8 7 5 9 4 6 0
1 2 3 7 8 5 9 4 6 0
Sample Output 1
Insertion Sort
1 2 3 5 7 8 9 4 6 0
Sample Input 2
10
3 1 2 8 7 5 9 4 0 6
1 3 2 8 5 7 4 9 0 6
Sample Output 2
Merge Sort
1 2 3 8 4 5 7 9 0 6
Program

#include <algorithm>
#include<iostream>
using namespace std;
int main() {
	int n;
	cin >> n;
	int *a = new int[n];
	int *b = new int[n];
	for (int i = 0; i < n; i++) cin >> a[i];
	for (int i = 0; i < n; i++) cin >> b[i];
	int i, j;
	for (i = 0; i < n - 1 && b[i] <= b[i + 1]; i++);
	for (j = i + 1; j < n&&a[j] == b[j]; j++);
	if (j == n){
		cout << "Insertion Sort" << endl;
		sort(a, a + i + 2);
		for (int i = 0; i < n; i++){
			cout << a[i];
			if (i != n - 1){
				cout << " ";
			}
		}
		cout << endl;
		return 0;
	}
	else{
		cout << "Merge Sort" << endl;
		bool isEqual = false;
		int k = 1;
		while (!isEqual){
			int i;
			for (i = 0; i < n; i++){
				if (a[i] != b[i]){
					break;
				}
			}
			if (i == n){
				isEqual = true;
			}
			k *= 2;
			for (int j = 0; j < n / k; j++){
				sort(a + j*k, a + (j + 1)*k);
			}
			sort(a + n / k*k, a + n);
		}
	}

	for (int i = 0; i < n; i++){
		cout << a[i];
		if (i != n - 1)
		{
			cout << " ";
		}
	}
	cout << endl;
	delete[] a;
	delete[] b;
	return 0;
}

1090 Highest Price in Supply Chain(25)

Description
A supply chain is a network of retailers（零售商）, distributors（经销商）, and suppliers（供应商）– everyone involved in moving a product from supplier to customer.
Starting from one root supplier, everyone on the chain buys products from one’s supplier in a price P and sell or distribute them in a price that is r% higher than P. It is assumed that each member in the supply chain has exactly one supplier except the root supplier, and there is no supply cycle.
Now given a supply chain, you are supposed to tell the highest price we can expect from some retailers.
Input Specification
Each input file contains one test case. For each case, The first line contains three positive numbers: N ($≤10^5$), the total number of the members in the supply chain (and hence they are numbered from 0 to N−1); P, the price given by the root supplier; and r, the percentage rate of price increment for each distributor or retailer. Then the next line contains N numbers, each number $S_{i}$ is the index of the supplier for the i-th member. $S_{root}$ for the root supplier is defined to be −1. All the numbers in a line are separated by a space.
Output Specification
For each test case, print in one line the highest price we can expect from some retailers, accurate up to 2 decimal places, and the number of retailers that sell at the highest price. There must be one space between the two numbers. It is guaranteed that the price will not exceed $10^{10}$.
Sample Input
9 1.80 1.00
1 5 4 4 -1 4 5 3 6
Sample Output
1.85 2
Program

#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
using namespace std;
struct Node{
	vector<int> child;
};
vector<Node> tree;
int N;
double P, r;
int maxDepth=-1, maxSum=0;
double maxPrice;
void preOrder(int root, int depth){
	if(depth>maxDepth){
		maxDepth=depth;
		maxSum=1;
		maxPrice=P*pow(1+r/100,maxDepth);
	}else if (depth==maxDepth){
		maxSum++;
	}
	for(int i=0;i<tree[root].child.size();i++){
		int childIdx=tree[root].child[i];
		preOrder(childIdx, depth+1);
	}
}
int main(){
	cin>>N>>P>>r;
	tree.resize(N);
	int root;
	for(int i=0;i<N;i++){
		int parent;
		cin>>parent;
		if(parent!=-1) tree[parent].child.push_back(i);
		else root=i;
	}
	preOrder(root, 0);
	printf("%.2f %d\n", maxPrice, maxSum);
	return 0;
}

1091 Acute Stroke(30)

Description
One important factor to identify acute stroke (急性脑卒中) is the volume of the stroke core. Given the results of image analysis in which the core regions are identified in each MRI slice, your job is to calculate the volume of the stroke core.
Input Specification
Each input file contains one test case. For each case, the first line contains 4 positive integers: M, N, L and T, where M and N are the sizes of each slice (i.e. pixels of a slice are in an M×N matrix, and the maximum resolution is 1286 by 128); L (≤60) is the number of slices of a brain; and T is the integer threshold (i.e. if the volume of a connected core is less than T, then that core must not be counted).
Then L slices are given. Each slice is represented by an M×N matrix of 0’s and 1’s, where 1 represents a pixel of stroke, and 0 means normal. Since the thickness of a slice is a constant, we only have to count the number of 1’s to obtain the volume. However, there might be several separated core regions in a brain, and only those with their volumes no less than T are counted. Two pixels are connected and hence belong to the same region if they share a common side, as shown by Figure 1 where all the 6 red pixels are connected to the blue one.

Figure 1

Output Specification
For each case, output in a line the total volume of the stroke core.
Sample Input
3 4 5 2
1 1 1 1
1 1 1 1
1 1 1 1
0 0 1 1
0 0 1 1
0 0 1 1
1 0 1 1
0 1 0 0
0 0 0 0
1 0 1 1
0 0 0 0
0 0 0 0
0 0 0 1
0 0 0 1
1 0 0 0
Sample Output
26
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
struct Node{
	int x,y,z;
	Node(){}
	Node(int X,int Y,int Z):x(X),y(Y),z(Z){}
};
int slice[1287][129][61]={0};
bool vis[1287][129][61]={false};
int M,N,L,T;
int sum=0;
const int step[6][3]={
	0,  0, -1,
	0,  0,  1,
	0,  1,  0,
	0, -1,  0,
	1,  0,  0,
	-1,  0,  0
};
bool judge(int x,int y,int z){
	if(x>=0&&x<M&&y>=0&&y<N&&z>=0&&z<L) return true;
	return false;
}
int BFS(int x,int y,int z){
	vis[x][y][z]=true;
	queue<Node> q;
	q.push(Node(x,y,z));
	int sum=1;
	while(!q.empty()){
		Node now=q.front();
		q.pop();
		for(int i=0;i<6;i++){
			int x=now.x+step[i][0];
			int y=now.y+step[i][1];
			int z=now.z+step[i][2];
			if(judge(x,y,z)&&!vis[x][y][z]&&slice[x][y][z]==1){
				vis[x][y][z]=true;
				q.push(Node(x,y,z));
				sum++;
			}
		}
	}
	return sum;
}
void BFSTraverse(){
	for(int z=0;z<L;z++){
		for(int x=0;x<M;x++){
			for(int y=0;y<N;y++){
				if(!vis[x][y][z]&&slice[x][y][z]==1){
					int tmp=BFS(x, y, z);
					if(tmp>=T) sum+=tmp;
				}
			}
		}
	}
}

int main(){
	cin>>M>>N>>L>>T;
	for(int z=0;z<L;z++){
		for(int x=0;x<M;x++){
			for(int y=0;y<N;y++){
				cin>>slice[x][y][z];
			}
		}
	}
	BFSTraverse();
	cout<<sum<<endl;
	return 0;
}

1092 To Buy or Not to Buy(20)

Description
Eva would like to make a string of beads with her favorite colors so she went to a small shop to buy some beads. There were many colorful strings of beads. However the owner of the shop would only sell the strings in whole pieces. Hence Eva must check whether a string in the shop contains all the beads she needs. She now comes to you for help: if the answer is Yes, please tell her the number of extra beads she has to buy; or if the answer is No, please tell her the number of beads missing from the string.
For the sake of simplicity, let’s use the characters in the ranges [0-9], [a-z], and [A-Z] to represent the colors. For example, the 3rd string in Figure 1 is the one that Eva would like to make. Then the 1st string is okay since it contains all the necessary beads with 8 extra ones; yet the 2nd one is not since there is no black bead and one less red bead.

ppRYYGrrYBR2258
ppRYYGrrYB225
YrR8RrY

Figure 1
Input Specification
Each input file contains one test case. Each case gives in two lines the strings of no more than 1000 beads which belong to the shop owner and Eva, respectively.
Output Specification
For each test case, print your answer in one line. If the answer is Yes, then also output the number of extra beads Eva has to buy; or if the answer is No, then also output the number of beads missing from the string. There must be exactly 1 space between the answer and the number.
Sample Input 1
ppRYYGrrYBR2258
YrR8RrY
Sample Output 1
Yes 8
Sample Input 2
ppRYYGrrYB225
YrR8RrY
Sample Output 2
No 2
Program

#include<iostream>
#include<cstring>
#include<map>
using namespace std;
string s1, s2;
map<char, int> m;
int main(){
	getline(cin, s1);
	getline(cin, s2);
	for(int i=0;i<s1.length();i++){
		if(m.find(s1[i])==m.end()){
			m[s1[i]]=1;
		}else{
			m[s1[i]]++;
		}
	}
	int missNum=0;
	for(int i=0;i<s2.length();i++){
		if(m.find(s2[i])!=m.end()){
			if(m[s2[i]]!=0){
				m[s2[i]]--;
			}else{
				missNum++;
			}
		}else{
			missNum++;
		}
	}
	if(missNum==0){
		cout<<"Yes "<<s1.length()-s2.length()<<endl;
	}else{
		cout<<"No "<<missNum<<endl;
	}
	return 0;
}

1093 Count PAT’s(25)

Description
The string APPAPT contains two PAT’s as substrings. The first one is formed by the 2nd, the 4th, and the 6th characters, and the second one is formed by the 3rd, the 4th, and the 6th characters.
Now given any string, you are supposed to tell the number of PAT’s contained in the string.
Input Specification
Each input file contains one test case. For each case, there is only one line giving a string of no more than $10^5$ characters containing only P, A, or T.
Output Specification
For each test case, print in one line the number of PAT’s contained in the string. Since the result may be a huge number, you only have to output the result moded by 1000000007.
Sample Input
APPAPT
Sample Output
2
Program

#include<iostream>
#include<cstring>
using namespace std;
int numP=0;
int numPA=0;
int numPAT=0;
string str;
int main(){
	cin>>str;
	for(int i=0;i<str.length();i++){
		if(str[i]=='P'){
			numP++;
		}else if(str[i]=='A'){
			numPA+=numP;
		}else if(str[i]=='T'){
			numPAT=(numPAT+numPA)%1000000007;
		}
	}
	cout<<numPAT<<endl;
	return 0;
}

1094 The Largest Generation(25)

Description
A family hierarchy is usually presented by a pedigree tree where all the nodes on the same level belong to the same generation. Your task is to find the generation with the largest population.
Input Specification
Each input file contains one test case. Each case starts with two positive integers N (<100) which is the total number of family members in the tree (and hence assume that all the members are numbered from 01 to N), and M (<N) which is the number of family members who have children. Then M lines follow, each contains the information of a family member in the following format:
ID K ID[1] ID[2] ... ID[K]
where ID is a two-digit number representing a family member, K (>0) is the number of his/her children, followed by a sequence of two-digit ID’s of his/her children. For the sake of simplicity, let us fix the root ID to be 01. All the numbers in a line are separated by a space.
Output Specification
For each test case, print in one line the largest population number and the level of the corresponding generation. It is assumed that such a generation is unique, and the root level is defined to be 1.
Sample Input
23 13
21 1 23
01 4 03 02 04 05
03 3 06 07 08
06 2 12 13
13 1 21
08 2 15 16
02 2 09 10
11 2 19 20
17 1 22
05 1 11
07 1 14
09 1 17
10 1 18
Sample Output
9 4
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
struct Node{
	vector<int> child;
};
vector<Node> tree;
int N,M;
int Max=1, Level=1;
void BFS(int root){
	queue<int> q;
	q.push(root);
	int levelSum=0;
	int level=1;
	int start=0, end=1;
	while(!q.empty()){
		int now=q.front();
		q.pop();
		for(int i=0;i<tree[now].child.size();i++){
			q.push(tree[now].child[i]);
			levelSum++;
		}
		start++;
		if(start==end){
			level++;
			start=0;
			end=levelSum;
			if(levelSum>Max){
				Max=levelSum;
				Level=level;
			}
			levelSum=0;
		}
	}
}
int main(){
	cin>>N>>M;
	tree.resize(N+1);
	for(int i=0;i<M;i++){
		int id, k, idj;
		cin>>id>>k;
		for(int j=0;j<k;j++){
			cin>>idj;
			tree[id].child.push_back(idj);
		}
	}
	BFS(1);
	cout<<Max<<" "<<Level<<endl;
	return 0;
}

1095 Cars on Campus(30)

Description
Zhejiang University has 8 campuses and a lot of gates. From each gate we can collect the in/out times and the plate numbers of the cars crossing the gate. Now with all the information available, you are supposed to tell, at any specific time point, the number of cars parking on campus, and at the end of the day find the cars that have parked for the longest time period.
Input Specification
Each input file contains one test case. Each case starts with two positive integers N ($≤10^4$), the number of records, and K ($≤8×10^4$) the number of queries. Then N lines follow, each gives a record in the format:
plate_number hh:mm:ss status
where plate_number is a string of 7 English capital letters or 1-digit numbers; hh:mm:ss represents the time point in a day by hour:minute:second, with the earliest time being 00:00:00 and the latest 23:59:59; and status is either in or out.
Note that all times will be within a single day. Each in record is paired with the chronologically next record for the same car provided it is an out record. Any in records that are not paired with an out record are ignored, as are out records not paired with an in record. It is guaranteed that at least one car is well paired in the input, and no car is both in and out at the same moment. Times are recorded using a 24-hour clock.
Then K lines of queries follow, each gives a time point in the format hh:mm:ss. Note: the queries are given in ascending order of the times.
Output Specification
For each query, output in a line the total number of cars parking on campus. The last line of output is supposed to give the plate number of the car that has parked for the longest time period, and the corresponding time length. If such a car is not unique, then output all of their plate numbers in a line in alphabetical order, separated by a space.
Sample Input
16 7
JH007BD 18:00:01 in
ZD00001 11:30:08 out
DB8888A 13:00:00 out
ZA3Q625 23:59:50 out
ZA133CH 10:23:00 in
ZD00001 04:09:59 in
JH007BD 05:09:59 in
ZA3Q625 11:42:01 out
JH007BD 05:10:33 in
ZA3Q625 06:30:50 in
JH007BD 12:23:42 out
ZA3Q625 23:55:00 in
JH007BD 12:24:23 out
ZA133CH 17:11:22 out
JH007BD 18:07:01 out
DB8888A 06:30:50 in
05:10:00
06:30:50
11:00:00
12:23:42
14:00:00
18:00:00
23:59:00
Sample Output
1
4
5
2
1
0
1
JH007BD ZD00001 07:20:09
Program

#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<map>
using namespace std;
bool shift=false;  //false 按车牌和时间排序，true，按时间排序
struct Car{
	string id;
	int time;
	string status;
	Car(){}
	Car(string Id, int Time, string Status):id(Id), time(Time), status(Status){}
	bool operator < (const Car &tmp) const{
		if(!shift){
			if(id!=tmp.id) return id<tmp.id;
			else return time<tmp.time;
		}else return time<tmp.time;
	}
};
map<string, int> parkTime;
int maxParkTime=0;
vector<Car> vec;
vector<Car> valid;
int n, k;
int timeToint(int hh, int mm, int ss){
	return hh*3600+mm*60+ss;
}
void intTotime(int ss){
	int hh=ss/3600;
	int mm=ss%3600/60;
	ss = ss%3600%60;
	printf(" %02d:%02d:%02d\n", hh,mm,ss);
}
int main(){
	cin>>n>>k;
	string id, status;
	int hh,mm,ss;
	for(int i=0;i<n;i++){
		cin>>id;
		scanf("%d:%d:%d", &hh, &mm, &ss);
		cin>>status;
		vec.push_back(Car(id, timeToint(hh,mm,ss), status));
	}
	sort(vec.begin(), vec.end());

	for(int i=0;i<n-1;){
		if(vec[i].id==vec[i+1].id
			&&vec[i].status=="in"
			&&vec[i+1].status=="out"){
			valid.push_back(vec[i]);
			valid.push_back(vec[i+1]);
			if(parkTime.find(vec[i].id)==parkTime.end()){
				parkTime[vec[i].id]=0;
			}
			parkTime[vec[i].id]+=vec[i+1].time-vec[i].time;
			maxParkTime=max(maxParkTime, parkTime[vec[i].id]);
			i+=2;
		}else i++;
	}

	shift=true;
	sort(valid.begin(),valid.end());

	int now=0, numCar=0;
	for(int i=0;i<k;i++){
		scanf("%d:%d:%d", &hh,&mm,&ss);
		int time=timeToint(hh,mm,ss);
		while(now<valid.size()&&valid[now].time<=time){
			if(valid[now].status=="in") numCar++;
			else numCar--;
			now++;
		}
		cout<<numCar<<endl;
	}
	bool isFirst=true;
	for(map<string,int>::iterator it=parkTime.begin();it!=parkTime.end();it++){
		if(it->second==maxParkTime){
			if(!isFirst) cout<<" ";
			else isFirst=false;
			cout<<it->first;
		}
	}
	intTotime(maxParkTime);
	return 0;
}

1096 Consecutive Factors(20)

Description
Among all the factors of a positive integer N, there may exist several consecutive numbers. For example, 630 can be factored as 3×5×6×7, where 5, 6, and 7 are the three consecutive numbers. Now given any positive N, you are supposed to find the maximum number of consecutive factors, and list the smallest sequence of the consecutive factors.
Input Specification
Each input file contains one test case, which gives the integer N ($1<N<2^{31}$).
Output Specification
For each test case, print in the first line the maximum number of consecutive factors. Then in the second line, print the smallest sequence of the consecutive factors in the format factor[1]*factor[2]*…*factor[k], where the factors are listed in increasing order, and 1 is NOT included.
Sample Input
630
Sample Output
3
567
Program

//2*3*4*5*7---连续积，而不是只要整除就以为可以，否则变成了2*3*4*5*6*7*8
//2*2*3*5--不要以为连续几个都可以被整除，比如2*3，就认为4不可以被整除
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
typedef long long LL;
LL n, start, maxLen=0;
int main(){
	cin>>n;
	for(LL i=2;i*i<=n;i++){
		LL j=i, len=0, tmp=1;
		while(n%(tmp*j)==0){
			tmp*=j;
			len++;
			j++;
		}
		if(len>maxLen){
			maxLen=len;
			start=i;
		}
	}
	if(maxLen==0) cout<<1<<endl<<n<<endl;
	else{
		cout<<maxLen<<endl;
		for(int i=0;i<maxLen;i++){
			if(i!=0) cout<<"*";
			cout<<start+i;
		}
		cout<<endl;
	}
	return 0;
}

1097 Deduplication on a Linked List(25)

Description
Given a singly linked list L with integer keys, you are supposed to remove the nodes with duplicated absolute values of the keys. That is, for each value K, only the first node of which the value or absolute value of its key equals K will be kept. At the mean time, all the removed nodes must be kept in a separate list. For example, given L being 21→-15→-15→-7→15, you must output 21→-15→-7, and the removed list -15→15.
Input Specification
Each input file contains one test case. For each case, the first line contains the address of the first node, and a positive N ($≤10^{5}$) which is the total number of nodes. The address of a node is a 5-digit nonnegative integer, and NULL is represented by −1.
Then N lines follow, each describes a node in the format:
Address Key Next
where Address is the position of the node, Key is an integer of which absolute value is no more than $10​^{4}$, and Next is the position of the next node.
Output Specification
For each case, output the resulting linked list first, then the removed list. Each node occupies a line, and is printed in the same format as in the input.
Sample Input
00100 5
99999 -7 87654
23854 -15 00000
87654 15 -1
00000 -15 99999
00100 21 23854
Sample Output
00100 21 23854
23854 -15 99999
99999 -7 -1
00000 -15 87654
87654 15 -1
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<cmath>
#include<set>
using namespace std;
struct Node{
	int address;
	int data;
	int next;
	Node(){}
	Node(int Address, int Data, int Next)
		:address(Address), data(Data), next(Next){}
};
vector<Node> vec;
vector<Node> order, result, del;
set<int> s;
int start, n;
int main(){
	cin>>start>>n;
	vec.resize(100001);
	for(int i=0;i<n;i++){
		int address, data, next;
		cin>>address>>data>>next;
		vec[address]=Node(address, data, next);
	}
	while(start!=-1){
		order.push_back(vec[start]);
		//printf("%05d %d %05d\n",vec[start].address, vec[start].data, vec[start].next);
		start=vec[start].next;
	}
	for(int i=0;i<order.size();i++){
		if(s.find(abs(order[i].data))==s.end()){
			result.push_back(order[i]);
			s.insert(abs(order[i].data));
		}else del.push_back(order[i]);
	}
	for(int i=0;i<result.size()-1;i++){
		result[i].next=result[i+1].address;
		printf("%05d %d %05d\n", result[i].address, result[i].data, result[i].next);
	}
	printf("%05d %d -1\n", result[result.size()-1].address, result[result.size()-1].data);
	if(del.size()!=0){
		for(int i=0;i<del.size()-1;i++){
			del[i].next=del[i+1].address;
			printf("%05d %d %05d\n", del[i].address, del[i].data, del[i].next);
		}
		printf("%05d %d -1", del[del.size()-1].address, del[del.size()-1].data);
	}
	return 0;
}

1098 Insertion or Heap Sort(25)

Description
According to Wikipedia:
Insertion sort iterates, consuming one input element each repetition, and growing a sorted output list. Each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list, and inserts it there. It repeats until no input elements remain.
Heap sort divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by extracting the largest element and moving that to the sorted region. it involves the use of a heap data structure rather than a linear-time search to find the maximum.
Now given the initial sequence of integers, together with a sequence which is a result of several iterations of some sorting method, can you tell which sorting method we are using?
Input Specification
Each input file contains one test case. For each case, the first line gives a positive integer N (≤100). Then in the next line, N integers are given as the initial sequence. The last line contains the partially sorted sequence of the N numbers. It is assumed that the target sequence is always ascending. All the numbers in a line are separated by a space.
Output Specification
For each test case, print in the first line either “Insertion Sort” or “Heap Sort” to indicate the method used to obtain the partial result. Then run this method for one more iteration and output in the second line the resulting sequence. It is guaranteed that the answer is unique for each test case. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line.
Sample Input 1
10
3 1 2 8 7 5 9 4 6 0
1 2 3 7 8 5 9 4 6 0
Sample Output 1
Insertion Sort
1 2 3 5 7 8 9 4 6 0
Sample Input 2
10
3 1 2 8 7 5 9 4 6 0
6 4 5 1 0 3 2 7 8 9
Sample Output 2
Heap Sort
5 4 3 1 0 2 6 7 8 9
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
vector<int> origin, vec, result;
int N;
bool isSame(vector<int> a, vector<int> b){
	for(int i=1;i<=N;i++){
		if(a[i]!=b[i]) return false;
	}
	return true;
}
bool insertSort(vector<int> &vec){
	bool flag=false;
	for(int i=2;i<=N;i++){
		if(i!=2&&isSame(vec, result)){ //至少一次插入操作！
			flag=true;
		}
		for(int j=i;j>=2&&vec[j]<vec[j-1];j--){
			swap(vec[j],vec[j-1]);
		}
		if(flag) return flag;
	}
	return flag;
}
void downAdjust(vector<int> &vec, int low, int high){
	int i=low, j=i*2;
	while(j<=high){
		if(j<high&&vec[j]<vec[j+1]){
			j++;
		}
		if(vec[j]>vec[i]){
			swap(vec[j], vec[i]);
			i=j;
			j=i*2;
		}else break;
	}
}
void heapSort(vector<int> &vec){
	for(int i=N/2;i>=1;i--){
		downAdjust(vec, i, N);
	}
	bool flag=false;
	for(int i=N;i>1;i--){
		if(isSame(vec, result)) flag=true;
		swap(vec[1], vec[i]);
		downAdjust(vec, 1, i-1);
		if(flag) return;
	}
}
void print(){
	for(int i=1;i<=N;i++){
		if(i!=1) cout<<" ";
		cout<<vec[i];
	}
	cout<<endl;
}
int main(){
	cin>>N;
	origin.resize(N+1);
	vec.resize(N+1);
	result.resize(N+1);
	for(int i=1;i<=N;i++){
		cin>>origin[i];
	}
	for(int i=1;i<=N;i++){
		cin>>result[i];
	}
	vec = origin;
	if(insertSort(vec)){
		cout<<"Insertion Sort"<<endl;
		print();
	}else{
		cout<<"Heap Sort"<<endl;
		vec=origin;
		heapSort(vec);
		print();
	}
	return 0;
}

1099 Build A Binary Search Tree(30)

Description
A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:
The left subtree of a node contains only nodes with keys less than the node’s key.
The right subtree of a node contains only nodes with keys greater than or equal to the node’s key.
Both the left and right subtrees must also be binary search trees.
Given the structure of a binary tree and a sequence of distinct integer keys, there is only one way to fill these keys into the tree so that the resulting tree satisfies the definition of a BST. You are supposed to output the level order traversal sequence of that tree. The sample is illustrated by Figure 1 and 2.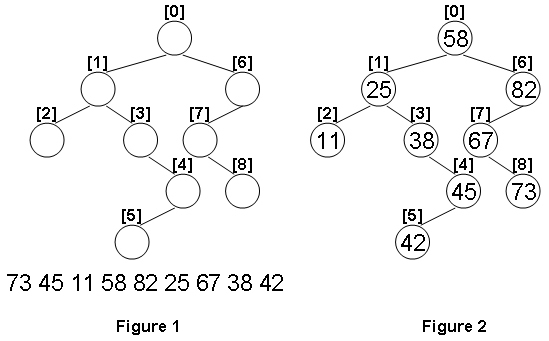

Input Specification
Each input file contains one test case. For each case, the first line gives a positive integer N (≤100) which is the total number of nodes in the tree. The next N lines each contains the left and the right children of a node in the format left_index right_index, provided that the nodes are numbered from 0 to N−1, and 0 is always the root. If one child is missing, then −1 will represent the NULL child pointer. Finally N distinct integer keys are given in the last line.
Output Specification
For each test case, print in one line the level order traversal sequence of that tree. All the numbers must be separated by a space, with no extra space at the end of the line.
Sample Input
9
1 6
2 3
-1 -1
-1 4
5 -1
-1 -1
7 -1
-1 8
-1 -1
73 45 11 58 82 25 67 38 42
Sample Output
58 25 82 11 38 67 45 73 42
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
struct Node{
	int data;
	int lchild, rchild;
};
vector<Node> tree;
int N;
int idx=0;
vector<int> vec;
void inOrder(int root){
	if(root==-1) return;
	inOrder(tree[root].lchild);
	tree[root].data=vec[idx++];
	inOrder(tree[root].rchild);
}
void levelOrder(int root){
	queue<int> q;
	q.push(root);
	bool bFirst=true;
	while(!q.empty()){
		int now=q.front();
		q.pop();
		if(bFirst) bFirst=false;
		else cout<<" ";
		cout<<tree[now].data;
		if(tree[now].lchild!=-1) q.push(tree[now].lchild);
		if(tree[now].rchild!=-1) q.push(tree[now].rchild);
	}
	cout<<endl;
}
int main(){
	cin>>N;
	tree.resize(N);
	vec.resize(N);
	for(int i=0;i<N;i++){
		cin>>tree[i].lchild>>tree[i].rchild;
	}
	for(int i=0;i<N;i++){
		cin>>vec[i];
	}
	sort(vec.begin(), vec.end());
	inOrder(0);
	levelOrder(0);
	return 0;
}

1100 Mars Numbers(20)

Description
People on Mars count their numbers with base 13:
Zero on Earth is called “tret” on Mars.
The numbers 1 to 12 on Earth is called “jan, feb, mar, apr, may, jun, jly, aug, sep, oct, nov, dec” on Mars, respectively.
For the next higher digit, Mars people name the 12 numbers as “tam, hel, maa, huh, tou, kes, hei, elo, syy, lok, mer, jou”, respectively.
For examples, the number 29 on Earth is called “hel mar” on Mars; and “elo nov” on Mars corresponds to 115 on Earth. In order to help communication between people from these two planets, you are supposed to write a program for mutual translation between Earth and Mars number systems.
Input Specification
Each input file contains one test case. For each case, the first line contains a positive integer N (<100). Then N lines follow, each contains a number in [0, 169), given either in the form of an Earth number, or that of Mars.
Output Specification
For each number, print in a line the corresponding number in the other language.
Sample Input
4
29
5
elo nov
tam
Sample Output
hel mar
may
115
13
Program

#include<iostream>
#include<cstdio>
#include<string>
using namespace std;
int main(){
	int N;
	cin >> N;
	string mess;
	string three = "";
	string fire[13] = { "tret", "jan", "feb", "mar", "apr", "may", "jun", "jly", "aug", "sep", "oct", "nov", "dec" };
	string radix[13] = { " ","tam", "hel", "maa", "huh", "tou", "kes", "hei", "elo", "syy", "lok", "mer", "jou" };
	int number = 0;
	getchar();          //使用getline时他会将第一次cin>>N的时候回车记录在内，从而少一次循环所以用getchar()捕捉那个回车
	for (int i = 0; i < N; i++){
		getline(cin, mess);
		if (isdigit(mess[0])){
			int x = stoi(mess);
			if (x < 13){
				cout << fire[x] << endl;
			}
			else{
				if (x % 13==0){
					cout << radix[x / 13] << endl;
				}
				else{
					cout << radix[x / 13] << " " << fire[x % 13] << endl;
				}
			}
		}
		else{
			number = 0;
			for (int i = 0; i < mess.length(); i += 4){
				string str = mess.substr(i, 3);
				for (int j = 0; j < 13; j++){
					if (str == fire[j]){
						number += j;
					}
					else if(str==radix[j]){
						number += j * 13;
					}
				}
			}
			cout << number << endl;
		}
	}
	return 0;
}

1101 Quick Sort(25)

Description
There is a classical process named partition in the famous quick sort algorithm. In this process we typically choose one element as the pivot. Then the elements less than the pivot are moved to its left and those larger than the pivot to its right. Given N distinct positive integers after a run of partition, could you tell how many elements could be the selected pivot for this partition?
For example, given N=5 and the numbers 1, 3, 2, 4, and 5. We have:

• 1 could be the pivot since there is no element to its left and all the elements to its right are larger than it;
• 3 must not be the pivot since although all the elements to its left are smaller, the number 2 to its right is less than it as well;
• 2 must not be the pivot since although all the elements to its right are larger, the number 3 to its left is larger than it as well;
• and for the similar reason, 4 and 5 could also be the pivot.
  Hence in total there are 3 pivot candidates.

Input Specification
Each input file contains one test case. For each case, the first line gives a positive integer N ($≤10^5$). Then the next line contains N distinct positive integers no larger than $10^9$. The numbers in a line are separated by spaces.
Output Specification
For each test case, output in the first line the number of pivot candidates. Then in the next line print these candidates in increasing order. There must be exactly 1 space between two adjacent numbers, and no extra space at the end of each line.
Sample Input
5
1 3 2 4 5
Sample Output
3
1 4 5
Program

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
vector<int> origin, order, result;
int n;
int main(){
	cin>>n;
	origin.resize(n);
	order.resize(n);
	for(int i=0;i<n;i++){
		cin>>origin[i];
		order[i]=origin[i];
	}
	sort(order.begin(), order.end());
	int leftMax=0;
	int sum=0;
	for(int i=0;i<n;i++){
		if(origin[i]==order[i]&&leftMax<origin[i]){
			sum++;
			result.push_back(origin[i]);
		}else if(leftMax<origin[i]){
			leftMax=origin[i];
		}
	}
	cout<<sum<<endl;
	for(int i=0;i<sum;i++){
		if(i!=0) cout<<" ";
		cout<<result[i];
	}
	cout<<endl;
	return 0;
}

1102 Invert a Binary Tree(25)

Description
The following is from Max Howell @twitter:
Google: 90% of our engineers use the software you wrote (Homebrew), but you can't invert a binary tree on a whiteboard so fuck off.`` Now it's your turn to prove that YOU CAN invert a binary tree! **Input Specification** Each input file contains one test case. For each case, the first line gives a positive integer N (≤10) which is the total number of nodes in the tree–and hence the nodes are numbered from 0 to N−1. Then N lines follow, each corresponds to a node from 0 to N−1, and gives the indices of the left and right children of the node. If the child does not exist, a-`` will be put at the position. Any pair of children are separated by a space.
Output Specification
For each test case, print in the first line the level-order, and then in the second line the in-order traversal sequences of the inverted tree. There must be exactly one space between any adjacent numbers, and no extra space at the end of the line.
Sample Input

8
1 -
- -
0 -
2 7
- -
- -
5 -
4 6

Sample Output
3 7 2 6 4 0 5 1
6 5 7 4 3 2 0 1
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
struct Node{
	char lchild, rchild;
};
vector<Node> tree;
vector<bool> vis;
int N;
void levelOrder(int root){
	queue<int> q;
	q.push(root);
	bool bFirst=true;
	while(!q.empty()){
		int front=q.front();
		q.pop();
		if(bFirst) bFirst=false;
		else cout<<" ";
		cout<<front;
		if(tree[front].lchild!='-') q.push(tree[front].lchild-'0');
		if(tree[front].rchild!='-') q.push(tree[front].rchild-'0');
	}
	cout<<endl;
}
bool bFirst=true;
void inOrder(int root){
	if(tree[root].lchild!='-') inOrder(tree[root].lchild-'0');
	if(bFirst) bFirst=false;
	else cout<<" ";
	cout<<root;
	if(tree[root].rchild!='-') inOrder(tree[root].rchild-'0');
}
int main(){
	cin>>N;
	tree.resize(N);
	vis.resize(N);
	fill(vis.begin(), vis.end(), false);
	for(int i=0;i<N;i++){
		cin>>tree[i].rchild>>tree[i].lchild;
		if(tree[i].lchild!='-') vis[tree[i].lchild-'0']=true;
		if(tree[i].rchild!='-') vis[tree[i].rchild-'0']=true;
	}
	int root;
	for(int i=0;i<N;i++){
		if(!vis[i]){
			root=i;
			break;
		}
	}
	levelOrder(root);
	inOrder(root);
	cout<<endl;
	return 0;
}

1103 Integer Factorization(30)

Description
The K−P factorization of a positive integer N is to write N as the sum of the P-th power of K positive integers. You are supposed to write a program to find the K−P factorization of N for any positive integers N, K and P.
Input Specification
Each input file contains one test case which gives in a line the three positive integers N (≤400), K (≤N) and P ($1<P≤7$). The numbers in a line are separated by a space.
Output Specification
For each case, if the solution exists, output in the format:
N = n[1]^P + ... n[K]^P
where n[i] (i = 1, ..., K) is the i-th factor. All the factors must be printed in non-increasing order.
Note: the solution may not be unique. For example, the 5-2 factorization of 169 has 9 solutions, such as 12^2+4^2+2^2+2^2+1^2, or 11^2+6^2+2^2+2^2+2^2, or more. You must output the one with the maximum sum of the factors. If there is a tie, the largest factor sequence must be chosen – sequence $\lbrace a_{1},a_{2},⋯,a_{K}\rbrace$ is said to be larger than $\lbrace b_{1},b_{2},⋯,b_{K}\rbrace$if there exists 1≤L≤K such that $a_{i}=b_{​i}$ for $i<L$ and $a_{L}>b_{L}$.
If there is no solution, simple output Impossible.
Sample Input 1
169 5 2
Sample Output 1
169 = 6^2 + 6^2 + 6^2 + 6^2 + 5^2
Sample Input 2
169 167 3
Sample Output 2
Impossible
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<cmath>
using namespace std;
int N, K, P;
vector<int> factor;
vector<int> vec, result;
int maxSum=0;
void init(){
	int tmp=1;
	while((int)pow(tmp, P)<=N){
		factor.push_back(tmp);
		tmp++;
	}
	reverse(factor.begin(), factor.end());
}
void DFS(int i, int sum, int facSum){
	if(sum>N||vec.size()>K) return;
	if(vec.size()==K&&sum==N){
		if(facSum>maxSum){
			maxSum=facSum;
			result.clear();
			for(int j=0;j<vec.size();j++) result.push_back(vec[j ]);
		}
		return;
	}

	vec.push_back(factor[i]);
	DFS(i, sum+(int)pow(factor[i], P),facSum+factor[i]);
	vec.pop_back();
	if(i<factor.size()-1){
		DFS(i+1, sum, facSum);
	}
}
int main(){
	cin>>N>>K>>P;
	init();
	DFS(0, 0, 0);
	if(result.size()==0) cout<<"Impossible"<<endl;
	else{
		cout<<N<<" =";
		for(int i=0;i<result.size();i++){
			cout<<" "<<result[i]<<"^"<<P;
			if(i!=result.size()-1) cout<<" +";
		}
		cout<<endl;
	}
	return 0;
}

1104 Sum of Number Segments(20)

Description
Given a sequence of positive numbers, a segment is defined to be a consecutive subsequence. For example, given the sequence { 0.1, 0.2, 0.3, 0.4 }, we have 10 segments: (0.1) (0.1, 0.2) (0.1, 0.2, 0.3) (0.1, 0.2, 0.3, 0.4) (0.2) (0.2, 0.3) (0.2, 0.3, 0.4) (0.3) (0.3, 0.4) and (0.4).
Now given a sequence, you are supposed to find the sum of all the numbers in all the segments. For the previous example, the sum of all the 10 segments is 0.1 + 0.3 + 0.6 + 1.0 + 0.2 + 0.5 + 0.9 + 0.3 + 0.7 + 0.4 = 5.0.
Input Specification
Each input file contains one test case. For each case, the first line gives a positive integer N, the size of the sequence which is no more than $10^5$. The next line contains N positive numbers in the sequence, each no more than 1.0, separated by a space.
Output Specification
For each test case, print in one line the sum of all the numbers in all the segments, accurate up to 2 decimal places.
Sample Input
4
0.1 0.2 0.3 0.4
Sample Output
5.00
Program

#include<iostream>
using namespace std;
int n;
int main(){
	cin>>n;
	double sum=0, x;
	for(int i=0;i<n;i++){
		cin>>x;
		sum+=x*(n-i)*(i+1);
	}
	printf("%.2f\n", sum);
	return 0;
}

1105 Spiral Matrix(25)

Description
This time your job is to fill a sequence of N positive integers into a spiral matrix in non-increasing order. A spiral matrix is filled in from the first element at the upper-left corner, then move in a clockwise spiral. The matrix has m rows and n columns, where m and n satisfy the following: m×n must be equal to N; m≥n; and m−n is the minimum of all the possible values.
Input Specification
Each input file contains one test case. For each case, the first line gives a positive integer N. Then the next line contains N positive integers to be filled into the spiral matrix. All the numbers are no more than $10^{4}$. The numbers in a line are separated by spaces.
Output Specification
For each test case, output the resulting matrix in m lines, each contains n numbers. There must be exactly 1 space between two adjacent numbers, and no extra space at the end of each line.
Sample Input
12
37 76 20 98 76 42 53 95 60 81 58 93
Sample Output
98 95 93
42 37 81
53 20 76
58 60 76
Program

#include<iostream>
#include<cstring>
#include<functional>
#include<algorithm>
#include<vector>
#include<cmath>
using namespace std;
int N, m, n;
vector<int> vec;
int main(){
	cin>>N;
	vec.resize(N);
	for(int i=0;i<N;i++) cin>>vec[i];
	m = ceil(sqrt(N));
	while(N%m!=0) m++;
	n = N/m;
	//cout<<m<<" "<<n<<endl;
	int** A=new int*[m];
	for(int i=0;i<m;i++) A[i]=new int[n];
	sort(vec.begin(), vec.end(), greater<int>());
	int idx=0;
	int left, right, top, bottom;
	left=0;
	right=n-1;
	top=0;
	bottom=m-1;
	while(idx<N){
		for(int i=left;i<=right&&idx<N;i++) A[top][i]=vec[idx++];
		top++;
		for(int i=top;i<=bottom&&idx<N;i++) A[i][right]=vec[idx++];
		right--;
		for(int i=right;i>=left&&idx<N;i--) A[bottom][i]=vec[idx++];
		bottom--;
		for(int i=bottom;i>=top&&idx<N;i--) A[i][left]=vec[idx++];
		left++;
	}
	for(int i=0;i<m;i++){
		for(int j=0;j<n;j++){
			if(j!=0) cout<<" ";
			cout<<A[i][j];
		}
		cout<<endl;
	}
	return 0;
}

1106 Lowest Price in Supply Chain(25)

Description
A supply chain is a network of retailers（零售商）, distributors（经销商）, and suppliers（供应商）– everyone involved in moving a product from supplier to customer.
Starting from one root supplier, everyone on the chain buys products from one’s supplier in a price P and sell or distribute them in a price that is r% higher than P. Only the retailers will face the customers. It is assumed that each member in the supply chain has exactly one supplier except the root supplier, and there is no supply cycle.
Now given a supply chain, you are supposed to tell the lowest price a customer can expect from some retailers.
Input Specification
Each input file contains one test case. For each case, The first line contains three positive numbers: N ($≤10^{5}$), the total number of the members in the supply chain (and hence their ID’s are numbered from 0 to N−1, and the root supplier’s ID is 0); P, the price given by the root supplier; and r, the percentage rate of price increment for each distributor or retailer. Then N lines follow, each describes a distributor or retailer in the following format:
K​i ID[1] ID[2] ... ID[Ki]
where in the i-th line, Ki is the total number of distributors or retailers who receive products from supplier i, and is then followed by the ID’s of these distributors or retailers. Kj being 0 means that the j-th member is a retailer. All the numbers in a line are separated by a space.
Output Specification
For each test case, print in one line the lowest price we can expect from some retailers, accurate up to 4 decimal places, and the number of retailers that sell at the lowest price. There must be one space between the two numbers. It is guaranteed that the all the prices will not exceed $10^10$.
Sample Input
10 1.80 1.00
3 2 3 5
1 9
1 4
1 7
0
2 6 1
1 8
0
0
0
Sample Output
1.8362 2
Program

#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
using namespace std;
const int MAXL=0x3f3f3f3f;
struct Node{
	vector<int> child;
};
vector<Node> tree;
int N;
double P, r;
int minLevel=MAXL, sum=0;
double minPrice;
void preOrder(int root, int level){
	if(tree[root].child.size()==0){
		if(level<minLevel){
			minLevel=level;
			sum=1;
		}else if(level== minLevel) sum++;
		return;
	}
	for(int i=0;i<tree[root].child.size();i++){
		preOrder(tree[root].child[i], level+1);
	}
}
int main(){
	cin>>N>>P>>r;
	tree.resize(N);
	for(int i=0;i<N;i++){
		int K, id;
		cin>>K;
		for(int j=0;j<K;j++){
			cin>>id;
			tree[i].child.push_back(id);
		}
	}
	preOrder(0, 0);
	minPrice=P*pow(1+r/100,minLevel);
	printf("%.4f %d\n", minPrice, sum);
	return 0;
}

1107 Social Clusters(30)

Description
When register on a social network, you are always asked to specify your hobbies in order to find some potential friends with the same hobbies. A social cluster is a set of people who have some of their hobbies in common. You are supposed to find all the clusters.
Input Specification
Each input file contains one test case. For each test case, the first line contains a positive integer N (≤1000), the total number of people in a social network. Hence the people are numbered from 1 to N. Then N lines follow, each gives the hobby list of a person in the format:
Ki: hi[1] hi[2] ... hi[Ki]
where Ki(>0) is the number of hobbies, and hi[j] is the index of the j-th hobby, which is an integer in [1, 1000].
Output Specification
For each case, print in one line the total number of clusters in the network. Then in the second line, print the numbers of people in the clusters in non-increasing order. The numbers must be separated by exactly one space, and there must be no extra space at the end of the line.
Sample Input
8
3: 2 7 10
1: 4
2: 5 3
1: 4
1: 3
1: 4
4: 6 8 1 5
1: 4
Sample Output
3
4 3 1
Program

#include<iostream>
#include<algorithm>
#include<cstring>
#include<functional>
#include<vector>
using namespace std;
vector<int> father;
vector<int> hobby;
vector<int> root;
int findFather(int x){
	if(x!=father[x]){
		father[x]=findFather(father[x]);
	}
	return father[x];
}
void unionSet(int a, int b){
	int fa=findFather(a);
	int fb=findFather(b);
	if(fa!=fb) father[fa]=fb;
}
int N;
int main(){
	cin>>N;
	father.resize(N+1);
	root.resize(N+1);
	hobby.resize(1001);
	for(int i=0;i<N+1;i++) father[i]=i;
	fill(hobby.begin(), hobby.end(), 0);
	fill(root.begin(), root.end(), 0);
	for(int i=1;i<=N;i++){
		int k;
		cin>>k;
		getchar();
		for(int j=0;j<k;j++){
			int h;
			cin>>h;
			if(hobby[h]==0) hobby[h]=i;
			unionSet(i, hobby[h]);
		}
	}
	for(int i=1;i<=N;i++){
		root[findFather(i)]++;
	}
	vector<int> vec;
	for(int i=1;i<=N;i++){
		if(root[i]!=0){
			vec.push_back(root[i]);
		}
	}
	sort(vec.begin(), vec.end(), greater<int>());
	cout<<vec.size()<<endl;
	for(int i=0;i<vec.size();i++){
		if(i!=0) cout<<" ";
		cout<<vec[i];
	}
	cout<<endl;
	return 0;
}

赏

Thank you for inviting me to have candy.

支付宝

微信