分类
k-近邻算法(KNN)
| k-近邻算法 | |
|---|---|
| 优点 | 精度高、对异常值不敏感,无数据输入假定。 |
| 缺点 | 计算复杂度高、空间复杂度高 |
| 适用数据范围 | 数值型和标称型 |
原理
1.假设有一个带有标签的样本数据集(训练样本集),其中包含每条数据与所属分类的对应关系。
2.输入没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进行比较。
I. 计算新数据与样本数据集中每条数据的距离。
II. 对求得的所有距离进行排序(从小到大,越小表示越相似)。
III.取前 k (k 一般小于等于 20 )个样本数据对应的分类标签。
3.求 k 个数据中出现次数最多的分类标签作为新数据的分类
模型
1 | from numpy import * |
1 | (4, 2) |
示例:改进约会网站匹配效果
处理数据
1 | from numpy import * |
Min-Max归一化
1 | def autoNorm(dataSet): |
测试算法
1 | from numpy import * |
1 | The classifier came back with: 3, the real answer is: 3 |
构建完整系统
1 | from numpy import * |
1 | percentage of time spent playing video games?10 |
示例:手写识别系统
图像转向量
1 | import numpy as np |
1 | [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 1. 1. 1. 0. 0. 0. 0. 0. 0. |
手写数字识别系统
1 | import numpy as np |
1 | the classifier came back with: 0, the real answer is : 0 |
主成分分析(PCA)
PCA
| 主成分分析 | |
|---|---|
| 优点 | 降低数据的复杂性、识别最重要的多个特征 |
| 缺点 | 不一定需要,且可能损失有用信息 |
| 使用数据类型 | 数值型数据 |
原理
1.找出第一个主成分的方向,也就是数据’方差最大’的方向。
2.找出第二个主成分的方向,也就是数据’方差次大’的方向,并且该方向与第一个主成分方向’正交(orthogonal 如果是二维空间就叫垂直)’。
3.通过这种方式计算出所有的主成分方向。
4.通过数据集的协方差矩阵及其特征值分析,我们就可以得到这些主成分的值。
5.一旦得到了协方差矩阵的特征值和特征向量,我们就可以保留最大的 N 个特征。这些特征向量也给出了 N 个最重要特征的真实结构,我们就可以通过将数据乘上这 N 个特征向量 从而将它转换到新的空间上。
为什么正交?
1.正交是为了数据有效性损失最小
2.正交的一个原因是特征值的特征向量是正交的
实现
1 | import numpy as np |
1 | [['10.235186', '11.321997'], ... , ['10.334899', '8.543604']] |
可视化
1 | import numpy as np |
1 | (1000, 1) |
示例:利用PCA对半导体制造数据降维
1 | import numpy as np |
1 | nan |
主成分分析得到主成分数目
1 | import numpy as np |
可以看到前面15个值的数量级大于$10^{5}$,实际上以后的值都非常小,所以重要特征的数目很快下降。
实际上,有超过20%的特征值是0,意味着这些特征都是其他特征的副本,也就是说,它们可以通过其他特征来表示,而本身并没有提供额外的信息。
1 | [ 5.34151979e+07 2.17466719e+07 8.24837662e+06 2.07388086e+06 |
主成分分析
1 | import numpy as np |
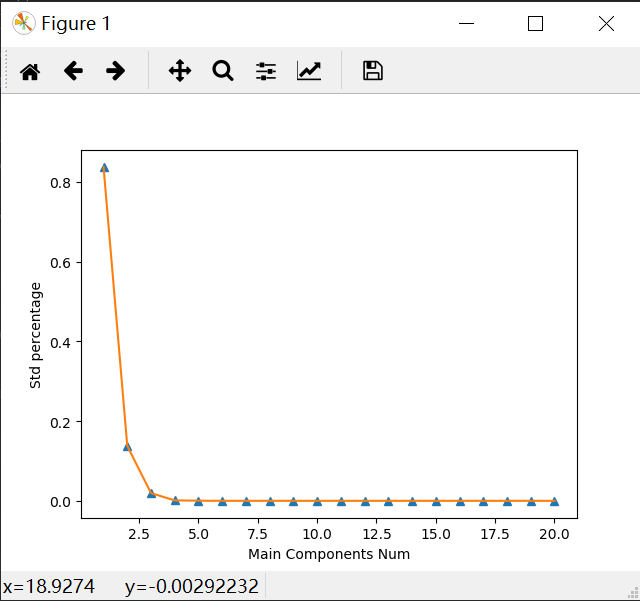
可以看到前几个特征占百分比很高了。
决策树
决策树的定义:
分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点(node)和有向边(directed edge)组成。结点有两种类型:内部结点(internal node)和叶结点(leaf node)。内部结点表示一个特征或属性(features),叶结点表示一个类(labels)。
用决策树对需要测试的实例进行分类:从根节点开始,对实例的某一特征进行测试,根据测试结果,将实例分配到其子结点;这时,每一个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分配,直至达到叶结点。最后将实例分配到叶结点的类中。
决策树的构造
| 决策树 | |
|---|---|
| 优点 | 计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不想管特征数据 |
| 缺点 | 可能会产生过度匹配的问题 |
| 适用数据类型 | 数值型和标称型 |
原理
熵 & 信息增益
熵(entropy): 熵指的是体系的混乱的程度,在不同的学科中也有引申出的更为具体的定义,是各领域十分重要的参量。
信息论(information theory)中的熵(香农熵): 是一种信息的度量方式,表示信息的混乱程度,也就是说:信息越有序,信息熵越低。例如:火柴有序放在火柴盒里,熵值很低,相反,熵值很高。
信息增益(information gain): 在划分数据集前后信息发生的变化称为信息增益。
1 | def createBranch(): |
信息增益
熵越高,则混合的数据也越多
注意:这里对数的底数是2,而深度学习中测试过,对数取自然对数e
1 | import math |
1 | [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']] ['no surfacing', 'flippers'] |
划分数据集
注意extend()与append()方法的区别,前者是将列表内容加入到之前的列表还是单个列表,后者是将列表加入形成多个列表
按照给定特征划分数据集
1 | def createDataSet(): |
1 | [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']] |
选择最好的数据集划分方式
1 | import math |
1 | 0 |
递归构建决策树
1 | import math |
1 | {'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}} |
注解绘制树形图
Matplotlib注解
1 | import matplotlib.pyplot as plt |
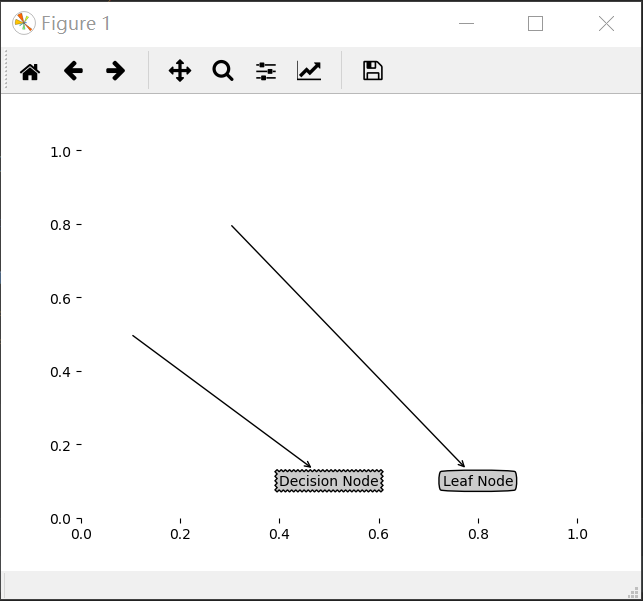
构造注解树
1 | import matplotlib.pyplot as plt |
1 | ['no surfacing'] |
打印注解树
1 | import matplotlib.pyplot as plt |
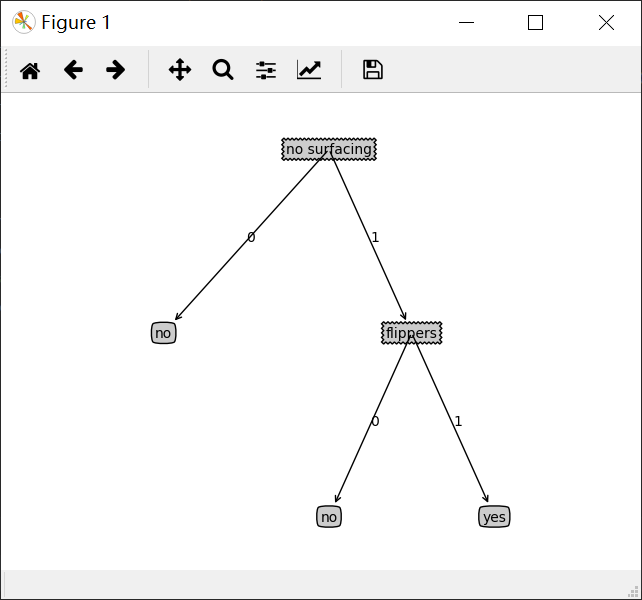
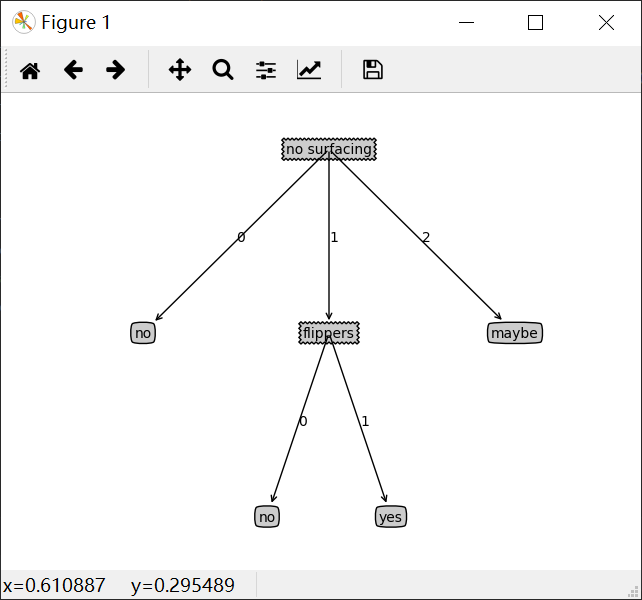
测试和存储分类器
测试算法
1 | import math |
1 | ['no surfacing', 'flippers'] |
存储
1 | def storeTree(inputTree, filename): |
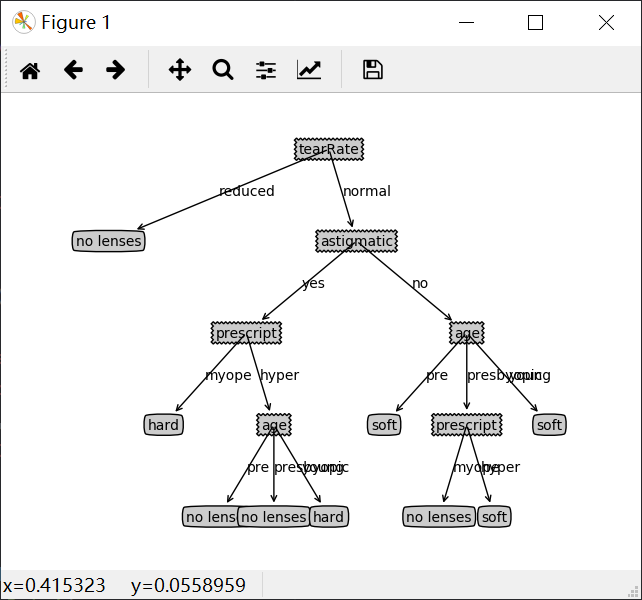
使用决策树预测隐形眼镜类型
1 | import math |
1 | {'tearRate': {'reduced': 'no lenses', 'normal': {'astigmatic': {'yes': {'prescript': {'myope': 'hard', 'hyper': {'age': {'pre': 'no lenses', 'presbyopic': 'no lenses', 'young': 'hard'}}}}, 'no': {'age': {'pre': 'soft', 'presbyopic': {'prescript': {'myope': 'no lenses', 'hyper': 'soft'}}, 'young': 'soft'}}}}}} |