Leetcode-动态规划

动态规划

线性DP

经典DP

53. 最大子序和

Description
给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
Example
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int* DP=new int[nums.size()];
        fill(DP,DP+nums.size(), INT_MIN);
        DP[0]=nums[0];
        for(int i=1;i<nums.size();i++){
            DP[i]=max(nums[i],DP[i-1]+nums[i]);
        }
        int MAX=INT_MIN;
        for(int i=0;i<nums.size();i++){
            if(DP[i]>MAX) MAX=DP[i];
        }
        return MAX;
    }
};

120. 三角形最小路径和

Description
给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。
Example
例如，给定三角形：
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

说明：
如果你可以只使用$O(n)$的额外空间（n 为三角形的总行数）来解决这个问题，那么你的算法会很加分。
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        int n=triangle.size();
        vector<int> &DP=triangle[n-1];
        for(int i=n-2;i>=0;i--){
            for(int j=0;j<i+1;j++){
                DP[j]=min(DP[j], DP[j+1])+triangle[i][j];
            }
        }
        return DP[0];
    }
};

132. 分割回文串 II

Description
给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。
返回符合要求的最少分割次数。
Example
示例:
输入: “aab”
输出: 1
解释: 进行一次分割就可将 s 分割成 [“aa”,”b”] 这样两个回文子串。
Program
思路
思路比较直观
（1）先isPal[i][j]的动规计算计算是否为回文串；
（2）设dp[i]为分割s为回文串的最小次数，状态转移方程为：
dp[i]=min(dp[j]+1)，当isPal[j+1][i]为true时；
这里有个关键点，整个串也算是自身的一个子串，纠结半天，觉得至少需要分割一次，即子串长度必须为[1,n-1]，想多了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    const int inf=0x3f3f3f3f;
    int minCut(string s) {
        int n=s.length();
        bool isPal[n][n];
        memset(isPal, false, sizeof(isPal));
        for(int i=0;i<n;i++){
            isPal[i][i]=true;
            if(i>0&&s[i-1]==s[i]) isPal[i-1][i]=true;
        }
        for(int len=3;len<=n;len++){
            for(int i=0;i+len-1<n;i++){
                int j=i+len-1;
                if(s[i]==s[j]) isPal[i][j]=isPal[i+1][j-1];
            }
        }
        int dp[n];
        memset(dp, inf, sizeof(dp));
        dp[0]=0;
        for(int i=1;i<n;i++){
            if(isPal[0][i]){ //整个串就是回文串了
                dp[i]=0;
                continue;
            }
            for(int j=i-1;j>=0;j--){
                if(isPal[j+1][i]) dp[i]=min(dp[i], dp[j]+1);
            }
        }
        return dp[n-1];
    }
};

152. 乘积最大子序列

Description
给定一个整数数组 nums ，找出一个序列中乘积最大的连续子序列（该序列至少包含一个数）。
Example
示例 1:
输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。

示例 2:
输入: [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
Program
很自然地想到$DP[i]=max(DP[i-1]nums[i], nums[i])$，但是数组存在负数，必须维护两个值，当前最小值和当前最大值，即
$imax=max(imaxnums[i], nums[i]),imin=min(imin*nums[i], nums[i])$，当出现负数交换两值！！！因为负数出现必然要用最小值（负数）才得到更大的数！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int n=nums.size();
        int ans=INT_MIN;
        int imax=1, imin=1;
        for(int i=0;i<n;i++){
            if(nums[i]<0) swap(imax, imin);
            imax=max(imax*nums[i], nums[i]);
            imin=min(imin*nums[i], nums[i]);
            ans=max(imax, ans);
        }
        return ans;
    }
};

174. 地下城游戏

Description
一些恶魔抓住了公主（P）并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士（K）最初被安置在左上角的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。
有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快到达公主，骑士决定每次只向右或向下移动一步。

编写一个函数来计算确保骑士能够拯救到公主所需的最低初始健康点数。
例如，考虑到如下布局的地下城，如果骑士遵循最佳路径 右 -> 右 -> 下 -> 下，则骑士的初始健康点数至少为 7。

1
2
3
-2 (K)	-3	3
-5	-10	1
10	30	-5 (P)

说明:
骑士的健康点数没有上限。
任何房间都可能对骑士的健康点数造成威胁，也可能增加骑士的健康点数，包括骑士进入的左上角房间以及公主被监禁的右下角房间。
Program
思路
与经典动规类似，从右下往左上DP，设DP[i][j]为从i，j出发，到达右下角的最低健康数：
$DP[i][j]=max(min(DP[i+1][j],DP[i][j+1])-dungeon[i][j], 1)$
即DP[i][j]与右侧与下方DP值有关，取最小minx，而[i,j]位置需要minx-dungeon[i][j],其值为非正，表示恰好够或者有多余健康值，当为0值时，只要需要1点健康值。
注意边界

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    const int inf=0x3f3f3f3f;
    int calculateMinimumHP(vector<vector<int>>& dungeon) {
        int m=dungeon.size(),n=dungeon[0].size();
        int DP[m+1][n+1];
        memset(DP, 0, sizeof(DP));
        for(int i=m-1;i>=0;i--){
            for(int j=n-1;j>=0;j--){
                if(i+1<m&&j+1<n) DP[i][j]=max(min(DP[i+1][j], DP[i][j+1])-dungeon[i][j],1);
                else if(i+1<m) DP[i][j]=max(DP[i+1][j]-dungeon[i][j], 1);
                else if(j+1<n) DP[i][j]=max(DP[i][j+1]-dungeon[i][j], 1);
                else DP[i][j]=max(1-dungeon[i][j], 1);
            }
        }
        return DP[0][0];
    }
};

198. 打家劫舍

Description
你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。
Example
示例 1:
输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。

示例 2:
输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int rob(vector<int>& nums) {
        vector<int> DP;
        DP.resize(nums.size());
        for(int i=0;i<nums.size();i++) DP[i]=nums[i];

        for(int i=2;i<nums.size();i++){
            if(i-3<0){
                DP[i]+=DP[i-2];
            }else{
                DP[i] += max(DP[i-2], DP[i-3]);
            }
        }

        int maxN=0;
        for(int i=0;i<nums.size();i++){
            if(maxN<DP[i]) maxN=DP[i];
        }
        return maxN;
    }
};

213. 打家劫舍 II

Description
你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。
Example
示例 1:
输入: [2,3,2]
输出: 3
解释: 你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

示例 2:
输入: [1,2,3,1]
输出: 4
解释: 你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。
偷窃到的最高金额 = 1 + 3 = 4 。
Program
由于成环，所以首尾两个数必须不能同时取，则划分成两个子问题：
①不包含第一个数
②不包含最后一个数
两个子问题下求解的不成环单列最大值中取最值就是最终答案！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    int cal(vector<int>& nums){
        if(nums.size()==0) return 0;
        if(nums.size()==1) return nums[0];
        vector<int> DP;
        DP.resize(nums.size());
        for(int i=0;i<nums.size();i++) DP[i]=nums[i];
        int ans=max(DP[0], DP[1]);
        for(int i=2;i<nums.size();i++){
            if(i-3<0){
                DP[i]+=DP[i-2];
            }else{
                DP[i] += max(DP[i-2], DP[i-3]);
            }
            ans=max(ans, DP[i]);
        }
        return ans;
    }
    int rob(vector<int>& nums) {
        if(nums.size()==0) return 0;
        if(nums.size()==1) return nums[0];
        vector<int> x1(nums.begin(), nums.end()-1);
        vector<int> x2(nums.begin()+1, nums.end());
        int ans1=cal(x1);
        int ans2=cal(x2);
        return max(ans1, ans2);
    }
};

256. 粉刷房子

Description
假如有一排房子，共 n 个，每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种，你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。
当然，因为市场上不同颜色油漆的价格不同，所以房子粉刷成不同颜色的花费成本也是不同的。每个房子粉刷成不同颜色的花费是以一个 n x 3 的矩阵来表示的。
例如，costs[0][0] 表示第 0 号房子粉刷成红色的成本花费；costs[1][2] 表示第 1 号房子粉刷成绿色的花费，以此类推。请你计算出粉刷完所有房子最少的花费成本。
注意：
所有花费均为正整数。
Example
示例：
输入: [[17,2,17],[16,16,5],[14,3,19]]
输出: 10
解释: 将 0 号房子粉刷成蓝色，1 号房子粉刷成绿色，2 号房子粉刷成蓝色。
最少花费: 2 + 5 + 3 = 10。
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int minCost(vector<vector<int>>& costs) {
        if(costs.size()==0) return 0;
        int n=costs.size();
        int DP[n][3];
        memset(DP, 0, sizeof(DP));
        for(int i=0;i<3;i++) DP[0][i]=costs[0][i];
        for(int i=1;i<n;i++){
            for(int j=0;j<3;j++){
                DP[i][j]=costs[i][j];
                DP[i][j]+=min(DP[i-1][j-1<0?2:j-1], DP[i-1][j+1>2?0:j+1]);
            }
        }
        int ans=INT_MAX;
        for(int i=0;i<3;i++) ans=min(ans, DP[n-1][i]);
        return ans;
    }
};

276. 栅栏涂色

Description
有 k 种颜色的涂料和一个包含 n 个栅栏柱的栅栏，每个栅栏柱可以用其中一种颜色进行上色。

你需要给所有栅栏柱上色，并且保证其中相邻的栅栏柱 最多连续两个 颜色相同。然后，返回所有有效涂色的方案数。

注意:
n 和 k 均为非负的整数。
Example
示例:
输入: n = 3，k = 2
输出: 6
解析: 用 c1 表示颜色 1，c2 表示颜色 2，所有可能的涂色方案有:

1
2
3
4
5
6
7
8
            柱 1    柱 2   柱 3     
-----      -----  -----  -----       
  1         c1     c1     c2
   2         c1     c2     c1
   3         c1     c2     c2
   4         c2     c1     c1 
  5         c2     c1     c2
   6         c2     c2     c1

Program
一般思路
设DP[i][j][c]为第i个栅栏连续j个颜色为c的个数，状态转移方程：

  • DP[i][2][c]=DP[i-1][1][c];
  • DP[i][1][c]=DP[i-1][1][cc!=c]+DP[i-1][2][cc!=c];
    无奈超时
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    class Solution {
    public:
        int numWays(int n, int k) {
            if(k==0||n==0) return 0;
            int DP[n][3][k];
            memset(DP, 0, sizeof(DP));
            for(int c=0;c<k;c++) DP[0][1][c]=1;
            for(int i=1;i<n;i++){
                for(int j=1;j<3;j++){
                    for(int c=0;c<k;c++){
                        if(j==2) DP[i][j][c]=DP[i-1][1][c];
                        if(j==1){
                            for(int cc=0;cc<k;cc++){
                                if(cc!=c) {
                                    DP[i][j][c]+=DP[i-1][1][cc];
                                    DP[i][j][c]+=DP[i-1][2][cc];
                                }
                            }
                        }
                    }
                }
            }
            int ans=0;
            for(int j=1;j<3;j++){
                for(int c=0;c<k;c++){
                    ans+=DP[n-1][j][c];
                }
            }
            return ans;
        }
    };

DP
设DP[i][0]为第i个栅栏与前一个不同的数量，DP[i][1]为第i个栅栏与前一个相同的数量：
DP[i][0]=(DP[i-1][0]+DP[i-1][1]) * (k-1);
DP[i][1]=DP[i-1][0];

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int numWays(int n, int k) {
        if(k==0||n==0) return 0;
        int DP[n][2];
        memset(DP, 0, sizeof(DP));
        DP[0][0]=k;
        for(int i=1;i<n;i++){
            DP[i][0]=(DP[i-1][1]+DP[i-1][0])*(k-1);
            DP[i][1]=DP[i-1][0];
        }
        return DP[n-1][0]+DP[n-1][1];
    }
};

状态压缩

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int numWays(int n, int k) {
        if(k==0||n==0) return 0;
        int DP[2]={k, 0};
        for(int i=1;i<n;i++){
            int tmp=DP[0];
            DP[0]=(DP[1]+DP[0])*(k-1);
            DP[1]=tmp;
        }
        return DP[0]+DP[1];
    }
};

300. 最长上升子序列

Description
给定一个无序的整数数组，找到其中最长上升子序列的长度。
Example
示例:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。
说明:

可能会有多种最长上升子序列的组合，你只需要输出对应的长度即可。
你算法的时间复杂度应该为 $O(n^2)$ 。
进阶: 你能将算法的时间复杂度降低到 $O(n\log{n})$ 吗?
Program
DP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.size()==0) return 0;
        int n=nums.size();
        vector<int> DP(n, 1);
        int ans=1;
        for(int i=1;i<n;i++){
            for(int j=0;j<i;j++){
                if(nums[i]>nums[j]) DP[i]=max(DP[i], DP[j]+1);
            }
            ans=max(ans, DP[i]);
        }
        return ans;
    }
};

贪心+二分
维护一个递增序列，维持其尾部尽可能小，因为这样可以使得序列尽可能长。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.size()==0) return 0;
        int n=nums.size();
        vector<int> tail(n, 0);
        int res=0;
        for(int x:nums){
            int i=0, j=res;
            while(i<j){ //找比x大的最小元素的位置
                int mid=(i+j)/2;
                if(tail[mid]<x) i=mid+1;
                else j=mid;
            }
            tail[i]=x;
            if(j==res) res++;
        }
        return res;
    }
};

354. 俄罗斯套娃信封问题

Description
给定一些标记了宽度和高度的信封，宽度和高度以整数对形式 (w, h) 出现。当另一个信封的宽度和高度都比这个信封大的时候，这个信封就可以放进另一个信封里，如同俄罗斯套娃一样。
请计算最多能有多少个信封能组成一组“俄罗斯套娃”信封（即可以把一个信封放到另一个信封里面）。
说明:
不允许旋转信封。
Example
示例:
输入: envelopes = [[5,4],[6,4],[6,7],[2,3]]
输出: 3
解释: 最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。
Program
常规DP
（1）先对信封按照w，h升序排列，然后DP；
（2）设DP[i]表示以i为结尾的最大嵌套次数，则状态转移方程：
DP[i]=max(DP[j])+1;
时间复杂度：$O(n^2)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int maxEnvelopes(vector<vector<int>>& envelopes) {
        if(envelopes.size()==0) return 0;
        int n=envelopes.size();
        sort(envelopes.begin(), envelopes.end(), [](const vector<int>& a, const vector<int>& b){
            if(a[0]==b[0]) return a[1]<b[1];
            return a[0]<b[0];
        });
        int dp[n];
        fill(dp, dp + n, 1);
        int ans=1;
        for(int i=1;i<n;i++){
            for(int j=0;j<i;j++){
                if(envelopes[j][0]<envelopes[i][0]&&envelopes[j][1]<envelopes[i][1]) dp[i]=max(dp[i], dp[j]+1);
            }
            ans=max(ans, dp[i]);
        }
        return ans;
    }
};

二分
与最长上升子序列的二分法思路类似；
（1）先对w升序，h降序，关键在h降序，保证相同的w下，tail只保留较大的h，防止相同的w下，更大的h的信封套上相同w而h更小的信封；
（2）tail[i]表示长度i的上升子序列尾部元素，贪心地希望尾部元素更小，那么就能够使得整个上升子序列越大；
（3）二分找比当前元素x更大的最小元素进行替换，没找到那么就增加长度；
时间复杂度：$O(n\log{n})$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int maxEnvelopes(vector<vector<int>>& envelopes) {
        if(envelopes.size()==0) return 0;
        int n=envelopes.size();
        sort(envelopes.begin(), envelopes.end(), [](const vector<int>& a, const vector<int>& b){ //按w升序，h降序
            if(a[0]==b[0]) return a[1]>b[1];
            return a[0]<b[0];
        });
        int height[n];
        for(int i=0;i<n;i++) height[i]=envelopes[i][1];
        int tail[n];
        int len=0;
        for(int x:height){
            int left=0, right=len;
            while(left<right){
                int mid=left+(right-left)/2;
                if(tail[mid]>=x) right=mid;
                else left=mid+1;
            }
            tail[left]=x;
            if(left==len) len++;
        }
        return len;
    }
};

面试题 17.08. 马戏团人塔

Description
有个马戏团正在设计叠罗汉的表演节目，一个人要站在另一人的肩膀上。出于实际和美观的考虑，在上面的人要比下面的人矮一点且轻一点。已知马戏团每个人的身高和体重，请编写代码计算叠罗汉最多能叠几个人。
Example
示例：
输入：height = [65,70,56,75,60,68] weight = [100,150,90,190,95,110]
输出：6
解释：从上往下数，叠罗汉最多能叠 6 层：(56,90), (60,95), (65,100), (68,110), (70,150), (75,190)
提示：
height.length == weight.length <= 10000
Program
常规DP
时间复杂度:$O(n^2)$
超时

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    struct Node{
        int h, w;
        Node(int _h, int _w):h(_h),w(_w){}
        bool operator < (const Node& tmp) const{
            if(h!=tmp.h) return h<tmp.h;
            else return w<tmp.w;
        }
    };
    int bestSeqAtIndex(vector<int>& height, vector<int>& weight) {
        if(height.size()==0) return 0;
        vector<Node> vec;
        int n=height.size();
        for(int i=0;i<n;i++){
            vec.push_back(Node(height[i], weight[i]));
        }
        sort(vec.begin(), vec.end());
        int DP[n];
        memset(DP, 0, sizeof(DP));
        int ans=0;
        for(int i=0;i<n;i++){
            DP[i]=1;
            for(int j=0;j<i;j++){
                if(vec[j].h<vec[i].h&&vec[j].w<vec[i].w){
                    DP[i]=max(DP[i], DP[j]+1);
                }
            }
            ans=max(DP[i], ans);
        }
        return ans;
    }
};

贪心+二分
根据上一题的思路，设tails[i]为以tails[i]为结尾长度为i+1的满足题目要求的序列

  • 这里先对h升序，再对w降序：
    升序保证不受h影响，只需要对w进行最长上升子序列求法，而对w降序则是在上述算法中避免h相同但较小的w更早出现的情况下不方便进行二分。—— 若h相同，较小的w先出现，那么较大的w出现时二分如何进行？找第一个大于等于w的位置？错误，明显不进行任何操作，但在进行二分的时候不方便体现，在h升序的基础上对w进行降序，则可以有效避免该情况的发生，因为h相同情况下，较大的w更早出现占据tails的某个位置，而较小的w则刚好在算法的执行当中替换掉较大的w的位置。
  • 二分找第一个比x大的元素位置进行替换
    因为tails[i]记录了长度为i+1结尾为tails[i]的满足题意的序列，那么贪心的希望tails[i]更小，那么后面得到的序列就会更长。
    时间复杂度：$O(n\log{n})$
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    class Solution {
    public:
        struct Node{
            int h, w;
            Node(){}
            Node(int _h, int _w):h(_h),w(_w){}
            bool operator < (const Node& tmp) const{
                if(h!=tmp.h) return h<tmp.h;
                else return w>tmp.w;
            }
        };
        int bestSeqAtIndex(vector<int>& height, vector<int>& weight) {
            if(height.size()==0) return 0;
            vector<Node> vec;
            int n=height.size();
            for(int i=0;i<n;i++){
                vec.push_back(Node(height[i], weight[i]));
            }
            sort(vec.begin(), vec.end());
            int tails[n]; //长度为i+1的以tails[i]为结尾的子序列
            // memset(tails, 0, sizeof(tails));
            int len=0;
            for(int i=0;i<n;i++){
                int w=vec[i].w;
                int left=0, right=len;
                while(left<right){ //找比x大的最小元素位置
                    int mid=left+(right-left)/2;
                    if(tails[mid]>=w) right=mid;
                    else left=mid+1;
                }
                tails[left]=w;
                if(left==len) len++;
            }
            return len;
        }
    };

    712. 两个字符串的最小ASCII删除和

Description
给定两个字符串s1, s2，找到使两个字符串相等所需删除字符的ASCII值的最小和。
Example
示例 1:
输入: s1 = “sea”, s2 = “eat”
输出: 231
解释: 在 “sea” 中删除 “s” 并将 “s” 的值(115)加入总和。
在 “eat” 中删除 “t” 并将 116 加入总和。
结束时，两个字符串相等，115 + 116 = 231 就是符合条件的最小和。

示例 2:
输入: s1 = “delete”, s2 = “leet”
输出: 403
解释: 在 “delete” 中删除 “dee” 字符串变成 “let”，
将 100[d]+101[e]+101[e] 加入总和。在 “leet” 中删除 “e” 将 101[e] 加入总和。
结束时，两个字符串都等于 “let”，结果即为 100+101+101+101 = 403 。
如果改为将两个字符串转换为 “lee” 或 “eet”，我们会得到 433 或 417 的结果，比答案更大。
注意:

1
2
0 < s1.length, s2.length <= 1000。
所有字符串中的字符ASCII值在[97, 122]之间。

Program
就是要找最长公共子序列，同时满足最长子序列的和最大。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int minimumDeleteSum(string s1, string s2) {
        int m=s1.length();
        int n=s2.length();
        vector<vector<int>> S(m+1, vector<int>(n+1, 0));
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(s1[i-1]==s2[j-1]){
                    S[i][j]=S[i-1][j-1]+(int)s1[i-1];
                }else{
                    S[i][j]=max(S[i][j-1],S[i-1][j]);
                }
            }
        }
        int sum=0;
        for(int i=0;i<m;i++) sum+=(int)s1[i];
        for(int j=0;j<n;j++) sum+=(int)s2[j];
        return sum-2*S[m][n];
    }
};

746. 使用最小花费爬楼梯

Description
数组的每个索引作为一个阶梯，第 i个阶梯对应着一个非负数的体力花费值 costi。
每当你爬上一个阶梯你都要花费对应的体力花费值，然后你可以选择继续爬一个阶梯或者爬两个阶梯。
您需要找到达到楼层顶部的最低花费。在开始时，你可以选择从索引为 0 或 1 的元素作为初始阶梯。
Example
示例 1:
输入: cost = [10, 15, 20]
输出: 15
解释: 最低花费是从cost[1]开始，然后走两步即可到阶梯顶，一共花费15。

示例 2:
输入: cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
输出: 6
解释: 最低花费方式是从cost[0]开始，逐个经过那些1，跳过cost[3]，一共花费6。

注意：
cost 的长度将会在 [2, 1000]。
每一个 cost[i] 将会是一个Integer类型，范围为 [0, 999]。
Program
注意顶层不是最后n-1，而是n。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    const int inf=0x3f3f3f3f;
    int minCostClimbingStairs(vector<int>& cost) {
        int n=cost.size();
        int DP[n+1];
        memset(DP,inf,sizeof(DP));
        DP[0]=cost[0];
        DP[1]=cost[1];
        for(int i=2;i<=n;i++){
            DP[i]=min(DP[i-1], DP[i-2]);
            if(i<n) DP[i]+=cost[i];
        }
        return DP[n];
    }
};

799. 香槟塔

Description
我们把玻璃杯摆成金字塔的形状，其中第一层有1个玻璃杯，第二层有2个，依次类推到第100层，每个玻璃杯(250ml)将盛有香槟。

从顶层的第一个玻璃杯开始倾倒一些香槟，当顶层的杯子满了，任何溢出的香槟都会立刻等流量的流向左右两侧的玻璃杯。当左右两边的杯子也满了，就会等流量的流向它们左右两边的杯子，依次类推。（当最底层的玻璃杯满了，香槟会流到地板上）

例如，在倾倒一杯香槟后，最顶层的玻璃杯满了。倾倒了两杯香槟后，第二层的两个玻璃杯各自盛放一半的香槟。在倒三杯香槟后，第二层的香槟满了 - 此时总共有三个满的玻璃杯。在倒第四杯后，第三层中间的玻璃杯盛放了一半的香槟，他两边的玻璃杯各自盛放了四分之一的香槟，如下图所示。

现在当倾倒了非负整数杯香槟后，返回第 i 行 j 个玻璃杯所盛放的香槟占玻璃杯容积的比例（i 和 j都从0开始）。
Example
示例 1:
输入: poured(倾倒香槟总杯数) = 1, query_glass(杯子的位置数) = 1, query_row(行数) = 1
输出: 0.0
解释: 我们在顶层（下标是（0，0））倒了一杯香槟后，没有溢出，因此所有在顶层以下的玻璃杯都是空的。

示例 2:
输入: poured(倾倒香槟总杯数) = 2, query_glass(杯子的位置数) = 1, query_row(行数) = 1
输出: 0.5
解释: 我们在顶层（下标是（0，0）倒了两杯香槟后，有一杯量的香槟将从顶层溢出，位于（1，0）的玻璃杯和（1，1）的玻璃杯平分了这一杯香槟，所以每个玻璃杯有一半的香槟。

注意:
poured 的范围$[0, 10 ^ 9]$。
query_glass 和query_row 的范围 $[0, 99]$。
Program
DP
设DP[i][j]为[i,j]的香槟容量，rest[i][j]为[i,j]的剩余容量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    double champagneTower(int poured, int query_row, int query_glass) {
        double DP[100][100], rest[100][100];
        memset(DP, 0, sizeof(DP));
        memset(rest, 0, sizeof(rest));
        for(int i=0;i<100;i++){
            for(int j=0;j<=i;j++){
                if(i==0){
                    if(poured>=1) {DP[i][j]=1.0;rest[i][j]=(double)poured-1.0;}
                    continue;
                }
                DP[i][j]=(j-1>=0?rest[i-1][j-1]/2:0)+(j<=i-1?rest[i-1][j]/2:0);
                if(DP[i][j]>1.0){rest[i][j]=DP[i][j]-1.0; DP[i][j]=1.0;}
            }
        }
        return DP[query_row][query_glass];
    }
};

931. 下降路径最小和

Description
给定一个方形整数数组 A，我们想要得到通过 A 的下降路径的最小和。
下降路径可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列。
Example
示例：
输入：[[1,2,3],[4,5,6],[7,8,9]]
输出：12
解释：
可能的下降路径有：
[1,4,7], [1,4,8], [1,5,7], [1,5,8], [1,5,9]
[2,4,7], [2,4,8], [2,5,7], [2,5,8], [2,5,9], [2,6,8], [2,6,9]
[3,5,7], [3,5,8], [3,5,9], [3,6,8], [3,6,9]
和最小的下降路径是 [1,4,7]，所以答案是 12。

提示：
1 <= A.length == A[0].length <= 100
-100 <= A[i][j] <= 100
Program
思路
常规动规题：设DP[i][j]为从第i行j列出发，到达最底层的最小值：
递推公式：$DP[i][j]=\min \lbrace DP[i+1][j-1], DP[i+1][j], DP[i+1][j+1]\rbrace$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    const int inf=0x3f3f3f3f;
    int minFallingPathSum(vector<vector<int>>& A) {
        int n=A.size();
        int DP[n][n];
        memset(DP, inf, sizeof(DP));
        for(int i=n-1;i>=0;i--){
            for(int j=0;j<n;j++){
                if(i==n-1){
                    DP[i][j]=A[i][j];
                    continue;
                }
                if(j-1>=0) DP[i][j]=min(DP[i][j], DP[i+1][j-1]);
                DP[i][j]=min(DP[i][j], DP[i+1][j]);
                if(j+1<n) DP[i][j]=min(DP[i][j], DP[i+1][j+1]);
                DP[i][j]+=A[i][j];
            }
        }
        int ans=inf;
        for(int i=0;i<n;i++) ans=min(ans, DP[0][i]);
        return ans;
    }
};

1043. 分隔数组以得到最大和

Description
给你一个整数数组 arr，请你将该数组分隔为长度最多为 k 的一些（连续）子数组。分隔完成后，每个子数组的中的所有值都会变为该子数组中的最大值。
返回将数组分隔变换后能够得到的元素最大和。
注意，原数组和分隔后的数组对应顺序应当一致，也就是说，你只能选择分隔数组的位置而不能调整数组中的顺序。
Example
示例 1：
输入：arr = [1,15,7,9,2,5,10], k = 3
输出：84
解释：
因为 k=3 可以分隔成 [1,15,7] [9] [2,5,10]，结果为 [15,15,15,9,10,10,10]，和为 84，是该数组所有分隔变换后元素总和最大的。
若是分隔成 [1] [15,7,9] [2,5,10]，结果就是 [1, 15, 15, 15, 10, 10, 10] 但这种分隔方式的元素总和（76）小于上一种。

示例 2：
输入：arr = [1,4,1,5,7,3,6,1,9,9,3], k = 4
输出：83

示例 3：
输入：arr = [1], k = 1
输出：1

提示：
1 <= arr.length <= 500
0 <= arr[i] <= 109
1 <= k <= arr.length
Program
思路
$DP[i]=max(DP[i], DP[j]+max(A[j+1], … , A[i]))$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int maxSumAfterPartitioning(vector<int>& arr, int k) {
        int n=arr.size();
        vector<vector<int>> mx(n, vector<int>(n, 0));
        for(int i=0;i<n;i++){
            int tmp=0;
            for(int j=i;j<n;j++){
                tmp=max(tmp, arr[j]);
                mx[i][j]=tmp;
            }
        }
        vector<int> DP(n+1, 0);
        for(int i=1;i<=n;i++){
            for(int j=max(0, i-k);j<i;j++){
                DP[i]=max(DP[i], DP[j]+mx[j][i-1]*(i-j));
            }
        }
        return DP[n];
    }
};

逆序优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int maxSumAfterPartitioning(vector<int>& arr, int k) {
        int n=arr.size();
        vector<int> DP(n+1, 0);
        for(int i=1;i<=n;i++){
            int mx=0;
            for(int j=i-1;j>=max(0, i-k);j--){ //逆序找区间最值
                mx=max(mx, arr[j]);
                DP[i]=max(DP[i], DP[j]+mx*(i-j));
            }
        }
        return DP[n];
    }
};

1143. 最长公共子序列

Description
给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。
一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
例如，”ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。
若这两个字符串没有公共子序列，则返回 0。
Example
示例 1:
输入：text1 = “abcde”, text2 = “ace”
输出：3
解释：最长公共子序列是 “ace”，它的长度为 3。

示例 2:
输入：text1 = “abc”, text2 = “abc”
输出：3
解释：最长公共子序列是 “abc”，它的长度为 3。

示例 3:
输入：text1 = “abc”, text2 = “def”
输出：0
解释：两个字符串没有公共子序列，返回 0。

提示:
1 <= text1.length <= 1000
1 <= text2.length <= 1000
输入的字符串只含有小写英文字符。
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int m=text1.length(), n=text2.length();
        int DP[m+1][n+1];
        memset(DP, 0, sizeof(DP));
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(text1[i-1]==text2[j-1]) DP[i][j]=DP[i-1][j-1]+1;
                else DP[i][j]=max(DP[i-1][j], DP[i][j-1]);
            }
        }
        return DP[m][n];
    }
};

1641. 统计字典序元音字符串的数目

Description
给你一个整数 n，请返回长度为 n 、仅由元音 (a, e, i, o, u) 组成且按 字典序排列 的字符串数量。
字符串 s 按 字典序排列 需要满足：对于所有有效的 i，s[i] 在字母表中的位置总是与 s[i+1] 相同或在 s[i+1] 之前。
Example
示例 1：
输入：n = 1
输出：5
解释：仅由元音组成的 5 个字典序字符串为 [“a”,”e”,”i”,”o”,”u”]

示例 2：
输入：n = 2
输出：15
解释：仅由元音组成的 15 个字典序字符串为
[“aa”,”ae”,”ai”,”ao”,”au”,”ee”,”ei”,”eo”,”eu”,”ii”,”io”,”iu”,”oo”,”ou”,”uu”]
注意，”ea” 不是符合题意的字符串，因为 ‘e’ 在字母表中的位置比 ‘a’ 靠后

示例 3：
输入：n = 33
输出：66045

提示：
1 <= n <= 50
Program
设DP[i][n]表示以某个元音结尾的长为n的满足条件的字符串个数，其中[0,1,2,3,4]分别表示[a,e,i,o,u]；
状态转移方程：
DP[0][i]=DP[0][i-1];
DP[1][i]=DP[1][i-1]+DP[0][i-1];
DP[2][i]=DP[2][i-1]+DP[1][i-1]+DP[0][i-1];
DP[3][i]=DP[3][i-1]+DP[2][i-1]+DP[1][i-1]+DP[0][i-1];
DP[4][i]=DP[4][i-1]+DP[3][i-1]+DP[2][i-1]+DP[1][i-1]+DP[0][i-1];

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int countVowelStrings(int n) {
        int DP[5][n+1];
        memset(DP, 0, sizeof(DP));
        for(int i=0;i<5;i++) DP[i][1]=1;
        for(int i=2;i<=n;i++){
            DP[0][i]=DP[0][i-1];
            DP[1][i]=DP[1][i-1]+DP[0][i-1];
            DP[2][i]=DP[2][i-1]+DP[1][i-1]+DP[0][i-1];
            DP[3][i]=DP[3][i-1]+DP[2][i-1]+DP[1][i-1]+DP[0][i-1];
            DP[4][i]=DP[4][i-1]+DP[3][i-1]+DP[2][i-1]+DP[1][i-1]+DP[0][i-1];
        }
        int ans=0;
        for(int i=0;i<5;i++) ans+=DP[i][n];
        return ans;
    }
};

1626. 无矛盾的最佳球队

Description
假设你是球队的经理。对于即将到来的锦标赛，你想组合一支总体得分最高的球队。球队的得分是球队中所有球员的分数 总和 。
然而，球队中的矛盾会限制球员的发挥，所以必须选出一支 没有矛盾 的球队。如果一名年龄较小球员的分数 严格大于 一名年龄较大的球员，则存在矛盾。同龄球员之间不会发生矛盾。
给你两个列表 scores 和 ages，其中每组 scores[i] 和 ages[i] 表示第 i 名球员的分数和年龄。请你返回 所有可能的无矛盾球队中得分最高那支的分数 。
Example
示例 1：
输入：scores = [1,3,5,10,15], ages = [1,2,3,4,5]
输出：34
解释：你可以选中所有球员。

示例 2：
输入：scores = [4,5,6,5], ages = [2,1,2,1]
输出：16
解释：最佳的选择是后 3 名球员。注意，你可以选中多个同龄球员。

示例 3：
输入：scores = [1,2,3,5], ages = [8,9,10,1]
输出：6
解释：最佳的选择是前 3 名球员。

提示：
$1 <= scores.length, ages.length <= 1000$
$scores.length == ages.length$
$1 <= scores[i] <= 10^6$
$1 <= ages[i] <= 1000$
Program
思路
（1）首先根据年龄升序，年龄相同则根据分数升序排列；
（2）那么对于i，左边肯定年龄都不大于其自身年龄
（3）设DP[i]为以i为结尾的无矛盾分数最大值，状态转移方程：
①age[j]==age[i]:
DP[i]=max(DP[i], DP[j]+score[i])
②age[j]<age[i],那么仅当score[j]<=score[i]时：
DP[i]=max(DP[i], DP[j]+score[i])
时间复杂度：$O(n^2)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    struct Node{
        int score, age;
        Node(){}
        Node(int _score, int _age):score(_score), age(_age){}
        bool operator < (const Node& other) const{
            return age==other.age?score<other.score:age<other.age;
        }
    };
    int bestTeamScore(vector<int>& scores, vector<int>& ages) {
        vector<Node> vec;
        int n=scores.size();
        for(int i=0;i<n;i++) vec.push_back(Node(scores[i], ages[i]));
        sort(vec.begin(), vec.end());
        int DP[n];
        memset(DP, 0, sizeof(DP));
        int ans=0;
        for(int i=0;i<n;i++){
            DP[i]=vec[i].score;
            for(int j=0;j<i;j++){
                if(vec[j].age==vec[i].age) DP[i]=max(DP[i], DP[j]+vec[i].score);
                else if(vec[j].score<=vec[i].score) DP[i]=max(DP[i], DP[j]+vec[i].score);
            }
            ans=max(ans, DP[i]);
        }

        return ans;
    }
};

面试题 08.01. 三步问题

Description
三步问题。有个小孩正在上楼梯，楼梯有n阶台阶，小孩一次可以上1阶、2阶或3阶。实现一种方法，计算小孩有多少种上楼梯的方式。结果可能很大，你需要对结果模1000000007。
Example
示例1:
输入：n = 3
输出：4
说明: 有四种走法

示例2:
输入：n = 5
输出：13
提示:
n范围在[1, 1000000]之间
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    const int MOD=1e9+7;
    int waysToStep(int n) {
        int DP[n+3];
        memset(DP, 0, sizeof(DP));
        DP[0]=DP[1]=1;
        DP[2]=2;
        for(int i=3;i<=n;i++){
            DP[i]=((DP[i-1]+DP[i-2])%MOD+DP[i-3])%MOD;
        }
        return DP[n];
    }
};

面试题42. 连续子数组的最大和

Description
输入一个整型数组，数组里有正数也有负数。数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。
Example
示例1:
输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

提示：
1 <= arr.length <= 10^5
-100 <= arr[i] <= 100

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n=nums.size();
        int DP[n];
        DP[0]=nums[0];
        int ans=DP[0];
        for(int i=1;i<n;i++){
            DP[i]=max(DP[i-1]+nums[i],nums[i]);
            ans=max(ans, DP[i]);
        }
        return ans;
    }
};

面试题47. 礼物的最大价值

Description
在一个 mn 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？
*Example**
示例 1:
输入:

1
2
3
4
5
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]

输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物

提示：

1
2
0 < grid.length <= 200
0 < grid[0].length <= 200

Program
动规
状态转移方程：$DP[i][j]=grid[i][j]+max(DP[i+1][j],DP[i][j+1])$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int maxValue(vector<vector<int>>& grid) {
        //if(grid.size()==0) return 0;
        int m=grid.size();
        int n=grid[0].size();
        int DP[m][n];
        memset(DP, 0, sizeof(DP));
        for(int i=m-1;i>=0;i--){
            for(int j=n-1;j>=0;j--){
                DP[i][j]=grid[i][j];
                if(i+1<m&&j+1<n) DP[i][j]+=max(DP[i+1][j],DP[i][j+1]);
                else if(i+1<m) DP[i][j]+=DP[i+1][j];
                else if(j+1<n) DP[i][j]+=DP[i][j+1];
            }
        }
        return DP[0][0];
    }
};

空间优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int maxValue(vector<vector<int>>& grid) {
        //if(grid.size()==0) return 0;
        int m=grid.size();
        int n=grid[0].size();
        int DP[n];
        memset(DP, 0, sizeof(DP));
        for(int i=m-1;i>=0;i--){
            for(int j=n-1;j>=0;j--){
                if(i+1<m&&j+1<n) DP[j]=max(DP[j],DP[j+1]);
                else if(i+1<m) DP[j]=DP[j];
                else if(j+1<n) DP[j]=DP[j+1];
                DP[j]+=grid[i][j];
            }
        }
        return DP[0];
    }
};

面试题 16.17. 连续数列

Description
给定一个整数数组，找出总和最大的连续数列，并返回总和。
Example
示例：
输入： [-2,1,-3,4,-1,2,1,-5,4]
输出： 6
解释： 连续子数组 [4,-1,2,1] 的和最大，为 6。
进阶：
如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解
Program
动规
时间复杂度：$O(n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n=nums.size();
        int DP[n];
        memset(DP, 0, sizeof(DP));
        int ans=nums[0];
        DP[0]=nums[0];
        for(int i=1;i<n;i++){
            DP[i]=max(nums[i], DP[i-1]+nums[i]);
            ans=max(ans, DP[i]);
        }
        return ans;
    }
};

空间优化

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n=nums.size();
        int ans=nums[0];
        int s=nums[0];
        for(int i=1;i<n;i++){
            s=max(nums[i], s+nums[i]);
            ans=max(ans, s);
        }
        return ans;
    }
};

分治
和最大的连续序列只会出现在三个位置：
（1）数组左边；
（2）数组右边；
（3）数组中间；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int dfs(vector<int>& nums, int left, int right){
        if(left==right) return nums[left];
        int mid=left+(right-left)/2;
        int leftSum=dfs(nums, left, mid);
        int rightSum=dfs(nums, mid+1, right);
        int midLeftSum=0, midLeftMaxSum=-INT_MAX;
        for(int i=mid;i>=left;i--){
            midLeftSum+=nums[i];
            midLeftMaxSum=max(midLeftMaxSum, midLeftSum);
        }
        int midRightSum=0, midRightMaxSum=-INT_MAX;
        for(int i=mid+1;i<=right;i++){
            midRightSum+=nums[i];
            midRightMaxSum=max(midRightMaxSum, midRightSum);
        }
        return max(max(leftSum, rightSum), (midLeftMaxSum+midRightMaxSum));
    }
    int maxSubArray(vector<int>& nums) {
        int n=nums.size();
        return dfs(nums, 0, n-1);
    }
};

字符DP

10. 正则表达式匹配

Description
给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。

‘.’ 匹配任意单个字符
‘*’ 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

说明:
s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 。
*Example**
示例 1:
输入:
s = “aa”
p = “a”
输出: false
解释: “a” 无法匹配 “aa” 整个字符串。

示例 2:
输入:
s = “aa”
p = “a*”
输出: true
解释: 因为 ‘*’ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此，字符串 “aa” 可被视为 ‘a’ 重复了一次。

示例 3:
输入:
s = “ab”
p = “.*”
输出: true
解释: “.*” 表示可匹配零个或多个（’*’）任意字符（’.’）。

示例 4:
输入:
s = “aab”
p = “cab”
输出: true
解释: 因为 ‘*’ 表示零个或多个，这里 ‘c’ 为 0 个, ‘a’ 被重复一次。因此可以匹配字符串 “aab”。

示例 5:
输入:
s = “mississippi”
p = “misis*p.”
输出: false
Program
动态规划
状态转移方程：
（1）s[i]==p[j]或p[j]==’.’, DP[i][j]=DP[i-1][j-1];
（2）p[j]==’*’:
①s[i]==p[j], DP[i][j]=DP[i-1][j]||DP[i][j-2];
②s[i]!=p[j], DP[i][j]=DP[i][j-2];
时间复杂度：$O(mn)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    bool isMatch(string s, string p) {
        int m=s.length(), n=p.length();
        bool DP[m+1][n+1];
        memset(DP, false, sizeof(DP));
        DP[0][0]=true;
        for(int i=0;i<=m;i++){
            for(int j=1;j<=n;j++){
                if((i>=1&&s[i-1]==p[j-1])||p[j-1]=='.') DP[i][j]=(i>=1?DP[i-1][j-1]:false);
                else if(p[j-1]=='*'){
                    if(i>=1&&j>=2&&(s[i-1]==p[j-2]||p[j-2]=='.')){ //注意".*"组合
                        DP[i][j]=DP[i-1][j]||DP[i][j-2];
                    }else DP[i][j]=(j>=2?DP[i][j-2]:false);
                }
            }
        }
        return DP[m][n];
    }
};

32. 最长有效括号

Description
给定一个只包含 ‘(‘ 和 ‘)’ 的字符串，找出最长的包含有效括号的子串的长度。
Example
示例 1:
输入: “(()”
输出: 2
解释: 最长有效括号子串为 “()”

示例 2:
输入: “)()())”
输出: 4
解释: 最长有效括号子串为 “()()”
Program
①双指针
lb,rb分别记录左右括号个数：
（1）从左往右遍历，如果lb==rb，则更新最大长度，如果rb>lb，lb=rb=0；
这样的做法贪心地考虑了以当前字符下标结尾的有效括号长度，每次当右括号数量多于左括号数量的时候之前的字符我们都扔掉不再考虑，重新从下一个字符开始计算，但这样会漏掉一种情况，就是遍历的时候左括号的数量始终大于右括号的数量，例如”(()” ，这种时候最长有效括号是求不出来的。
（2）所以从右往左遍历：如果lb==rb，更新最大长度，如果lb>rb，lb=rb=0;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int longestValidParentheses(string s) {
        int ans=0;
        int lb=0, rb=0;
        int tmpLen=0;
        int n=s.length();
        for(int i=0;i<n;i++){
            if(s[i]=='(') lb++;
            else rb++;
            if(lb==rb) ans=max(ans, 2*rb);
            else if(rb>lb) rb=lb=0;
        }
        for(int i=n-1;i>=0;i--){
            if(s[i]=='(') lb++;
            else rb++;
            if(lb==rb) ans=max(ans, 2 * rb);
            else if(lb>rb) rb=lb=0;
        }
        return ans;
    }
};

②动态规划
设DP[i]为以i结尾的最长有效长度，那么s[i]==’(‘肯定为0，只有s[i]==’)’才有可能更新长度.
（1）s[i]==’)’且s[i-1]==’(‘: DP[i]=DP[i-1]+2；
（2）s[i]==’)’且s[i-1]==’)’：
如果s[i-1-DP[i-1]]==’(‘：DP[i]=DP[i-1]+2+DP[i-2-DP[i-1]] —— 即DP[i-1]这一段的前一个字符为’(‘，则DP[i]的长度应当是DP[i-1]+2，以及更前一段DP[i-2-DP[i-1]]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int longestValidParentheses(string s) {
        if(s.length()==0) return 0;
        int n=s.length();
        int ans=0;
        int DP[n];
        memset(DP, 0, sizeof(DP));
        for(int i=1;i<n;i++){
            if(s[i]==')'&&s[i-1]=='(') DP[i]=(i-2>=0)?DP[i-2]+2:2;
            if(s[i]==')'&&s[i-1]==')'){
                if(i-1-DP[i-1]>=0&&s[i-1-DP[i-1]]=='(') DP[i]=DP[i-1]+2+(i-2-DP[i-1]>=0?DP[i-2-DP[i-1]]:0);
            }
            ans=max(ans, DP[i]);
        }
        return ans;
    }
};

44. 通配符匹配

Description
给定一个字符串 (s) 和一个字符模式 (p) ，实现一个支持 ‘?’ 和 ‘ * ‘ 的通配符匹配。

‘ ? ‘ 可以匹配任何单个字符。
‘ * ‘ 可以匹配任意字符串（包括空字符串）。
两个字符串完全匹配才算匹配成功。

说明:

  • s 可能为空，且只包含从 a-z 的小写字母。
  • p 可能为空，且只包含从 a-z 的小写字母，以及字符 ? 和 * 。

Example
示例 1:
输入:

1
2
s = "aa"
p = "a"

输出: false
解释: “a” 无法匹配 “aa” 整个字符串。

示例 2:
输入:

1
2
s = "aa"
p = "*"

输出: true
解释: ‘*’ 可以匹配任意字符串。

示例 3:
输入:

1
2
s = "cb"
p = "?a"

输出: false
解释: ‘?’ 可以匹配 ‘c’, 但第二个 ‘a’ 无法匹配 ‘b’。

示例 4:
输入:

1
2
s = "adceb"
p = "*a*b"

输出: true
解释: 第一个 ‘‘ 可以匹配空字符串, 第二个 ‘‘ 可以匹配字符串 “dce”.

示例 5:
输入:

1
2
s = "acdcb"
p = "a*c?b"

输出: false
Program
动态规划
设DP[i][j]为s与p的前i，j字符串是否能匹配：
（1）s[i]==p[j]或p[j]==’？’, DP[i][j]=DP[i-1][j-1]，即匹配一个字符
（2）p[j]==’‘，DP[i][j]=DP[i][j-1]||DP[i-1][j]，即匹配0个或匹配当前s[i]，但是j不减，因为可以匹配多个字符，这里分两种情况：匹配0个或1个，递推过程中可以匹配n个。
边界：
DP[0][0]=true，两字符串为空，显然；
DP[i][0]=false，显然
**DP[0][j]，看情况，当前p的前j个字符都为’‘，为true，否则false！**

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    bool isMatch(string s, string p) {
        int m=s.length();
        int n=p.length();
        bool DP[m+1][n+1];
        memset(DP, false, sizeof(DP));
        DP[0][0]=true;
        for(int j=1;j<=n;j++){ //s为空，p的前j子串只有全为'*'才为真
            if(p[j-1]=='*') DP[0][j]=true;
            else break;
        }
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(s[i-1]==p[j-1]||p[j-1]=='?') DP[i][j]=DP[i-1][j-1];
                else if(p[j-1]=='*') DP[i][j]= DP[i][j-1] || DP[i-1][j];
            }
        }
        return DP[m][n];
    }
};

91. 解码方法

Description
一条包含字母 A-Z 的消息通过以下方式进行了编码：
‘A’ -> 1
‘B’ -> 2
…
‘Z’ -> 26
给定一个只包含数字的非空字符串，请计算解码方法的总数。
Example
示例 1:
输入: “12”
输出: 2
解释: 它可以解码为 “AB”（1 2）或者 “L”（12）。

示例 2:
输入: “226”
输出: 3
解释: 它可以解码为 “BZ” (2 26), “VF” (22 6), 或者 “BBF” (2 2 6) 。
Program
计算DP[n]时，
①若s[n]满足要求，DP[n]=DP[n-1];否则0;
②若s[n-1]与s[n]构成两位数满足条件(9<value<27), DP[n]+=DP[n-2];如果value==0,直接return 0;
注意DP[2]是关键！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int numDecodings(string s) {
        int n=s.length();
        if(s[0]=='0') return 0;
        if(n==1) return 1;
        vector<int> DP(n, 0);
        DP[0]=1;
        int value=(s[0]-'0')*10+(s[1]-'0');
        if(value==10||value==20) DP[1]=1;
        else if(value>9&&value<27) DP[1]=2;
        else if(s[1]=='0') DP[1]=0;
        else DP[1]=1;
        for(int i=2;i<n;i++){
            value=(s[i-1]-'0')*10+(s[i]-'0');
            if(s[i]!='0') DP[i]=DP[i-1];
            if(value==0) return 0;
            if(value>9&&value<27) DP[i]+=DP[i-2];
        }
        return DP[n-1];
    }
};

97. 交错字符串

Description
给定三个字符串 s1, s2, s3, 验证 s3 是否是由 s1 和 s2 交错组成的。
Example
示例 1:
输入: s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbcbcac”
输出: true

示例 2:
输入: s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbbaccc”
输出: false
Program
字符DP
字符DP老套路，假设DP[i][j]表示s1前i个字符与s2前j个字符能够组成交错序列s3的前i+j个字符，故递推只需考虑s3[i+j-1]是否与s1[i-1]或s2[j-1]相等，
$DP[i][j]=(i>0&&DP[i-1][j]&&s1[i-1]==s3[i+j-1])||(j>0&&DP[i][j-1]&&s2[j-1]==s3[i+j-1]);$
注意：
m+n!=l，长度不等，直接false;
边界：DP[0][0]=true；
有可能一直是s1或s2的前几个元素与s3匹配，所以DP[m+1][n+1]必须从0开始DP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        int m=s1.length(), n=s2.length(), l=s3.length();
        if(m+n!=l) return false;
        bool DP[m+1][n+1];
        memset(DP, false, sizeof(DP));
        DP[0][0]=true;
        for(int i=0;i<=m;i++){ //从0开始，因为可能其中一个为空
            for(int j=0;j<=n;j++){
                if(i==0&&j==0) continue; //特判
                DP[i][j] = (i>0&&DP[i-1][j]&&s1[i-1]==s3[i+j-1])||(j>0&&DP[i][j-1]&&s2[j-1]==s3[i+j-1]);
            }
        }
        return DP[m][n];
    }
};

139. 单词拆分

Description
给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
说明：
拆分时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。
Example
示例 1：
输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以被拆分成 “leet code”。

示例 2：
输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解释: 返回 true 因为 “applepenapple” 可以被拆分成 “apple pen apple”。
注意你可以重复使用字典中的单词。

示例 3：
输入: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出: false
Program
DP[n]=DP[i]&&has(s(i+1, n))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> st(wordDict.begin(), wordDict.end());
        int n=s.length();
        vector<bool> DP(n+1, false);
        DP[0]=true;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=i;j++){
                if(DP[j-1]&&st.find(s.substr(j-1, i-j+1))!=st.end()){
                    DP[i]=true;
                    break;
                }
            }
        }
        return DP[n];
    }
};

字典树优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
public:
    struct Trie{
        bool isEnd;
        Trie* next[26];
        Trie(){
            isEnd=false;
            for(int i=0;i<26;i++) next[i]=NULL;
        }
    };
    void insertStr(Trie* root, string str){
        Trie* node=root;
        for(int i=str.length()-1;i>=0;i--){
            int t=str[i]-'a';
            if(node->next[t]==NULL) node->next[t]=new Trie();
            node=node->next[t];
        }
        node->isEnd=true;
    }
    bool wordBreak(string s, vector<string>& wordDict) {
        int n=s.length();
        vector<bool> DP(n+1, false);
        Trie* root=new Trie();
        for(string& str:wordDict) insertStr(root, str);
        DP[0]=true;
        for(int i=1;i<=n;i++){
            Trie* node=root;
            for(int j=i;j>=1;j--){
                int t=s[j-1]-'a';
                if(node->next[t]==NULL) break;
                node=node->next[t];
                if(node->isEnd) DP[i]=DP[j-1];
                if(DP[i]) break;
            }
        }
        return DP[n];
    }
};

面试题 17.13. 恢复空格

Description
哦，不！你不小心把一个长篇文章中的空格、标点都删掉了，并且大写也弄成了小写。像句子”I reset the computer. It still didn’t boot!”已经变成了”iresetthecomputeritstilldidntboot”。在处理标点符号和大小写之前，你得先把它断成词语。当然了，你有一本厚厚的词典dictionary，不过，有些词没在词典里。假设文章用sentence表示，设计一个算法，把文章断开，要求未识别的字符最少，返回未识别的字符数。
注意：本题相对原题稍作改动，只需返回未识别的字符数
Example
示例：
输入：
dictionary = [“looked”,”just”,”like”,”her”,”brother”]
sentence = “jesslookedjustliketimherbrother”
输出： 7
解释： 断句后为”jess looked just like tim her brother”，共7个未识别字符。
提示：
0 <= len(sentence) <= 1000
dictionary中总字符数不超过 150000。
你可以认为dictionary和sentence中只包含小写字母。
Program
字符DP
与单词拆分类似，设DP[i]为前i个字符最小未识别数，那么：
（1）$j<i$且sentence[j:i]子串能在字典中找到，则DP[i]=min(DP[i],DP[j-1]);
（2）否则，DP[i]=DP[i-1]+1，即第i个字符也没有被识别。
超时。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int respace(vector<string>& dictionary, string sentence) {
        if(sentence.length()==0) return 0;
        int n=sentence.length();
        unordered_set<string> st(dictionary.begin(), dictionary.end());
        int DP[n];
        memset(DP, 0, sizeof(DP));
        for(int i=0;i<n;i++){
            DP[i]=1+(i>0?DP[i-1]:0);
            for(int j=0;j<=i;j++){
                if(st.find(sentence.substr(j,i-j+1))!=st.end()){
                    int t=(j>0)?DP[j-1]:0;
                    DP[i]=min(DP[i], t);
                }
            }
        }
        return DP[n-1];
    }
};

字典树优化
上面方法中，从前往后遍历j可以优化，因为sentence[j:i]这个子串，j递增时，
不失一般性，设$j_1<j_2$，则sentence[j_1:i]和sentence[j_2:i]为两个可能子串，如果后者已经不可能为字典内的单词，那么前者就已经不用算了！
（1）j从i递减遍历：
（2）若[j,i]子串不在字典树中，提前终止；
（3）若[j,i]子串在字典树中，DP[i]=min(DP[i],DP[j-1])；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
public:
    struct Trie{
        bool isEnd;
        Trie* next[26];
        Trie(){
            isEnd=false;
            for(int i=0;i<26;i++) next[i]=NULL;
        }
    };
    void insertStr(Trie* root, string str){
        Trie* node=root;
        for(int i=str.length()-1;i>=0;i--){
            int t=str[i]-'a';
            if(node->next[t]==NULL) node->next[t]=new Trie();
            node=node->next[t];
        }
        node->isEnd=true;
    }
    int respace(vector<string>& dictionary, string sentence) {
        if(sentence.length()==0) return 0;
        int n=sentence.length();
        Trie* root=new Trie();
        for(string& str:dictionary) insertStr(root, str); //建立字典树
        int DP[n];
        memset(DP, 0, sizeof(DP));
        for(int i=0;i<n;i++){
            DP[i]=1+(i>0?DP[i-1]:0);
            Trie* node=root;
            for(int j=i;j>=0;j--){
                int t=sentence[j]-'a';
                if(node->next[t]==NULL) break; //[j,i]子串已经不再字典中，终止
                node=node->next[t];
                if(node->isEnd) DP[i]=min(DP[i], (j>0?DP[j-1]:0));
                if(DP[i]==0) break; //0已经最小了，终止

            }
        }
        return DP[n-1];
    }
};

467. 环绕字符串中唯一的子字符串

Description
把字符串 s 看作是“abcdefghijklmnopqrstuvwxyz”的无限环绕字符串，所以 s 看起来是这样的：”…zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd….”.
现在我们有了另一个字符串 p 。你需要的是找出 s 中有多少个唯一的 p 的非空子串，尤其是当你的输入是字符串 p ，你需要输出字符串 s 中 p 的不同的非空子串的数目。
注意: p 仅由小写的英文字母组成，p 的大小可能超过 10000。
Example
示例 1:
输入: “a”
输出: 1
解释: 字符串 S 中只有一个”a”子字符。

示例 2:
输入: “cac”
输出: 2
解释: 字符串 S 中的字符串“cac”只有两个子串“a”、“c”。.
Program
题目意思就是求字符串p中满足”…zabcd…”顺序的子串个数
设DP[i]是以字符p[i]为结尾的字符串最大长度，这是因为较长的以p[i]为结尾的子串串一定包含了较短的子串！不用重复计算！
DP[i]=max(DP[i], k)，其中k为满足条件子串长度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    bool isContinue(char pre, char next){
        if(pre=='z') return next=='a';
        return (pre+1) == next;
    }
    int findSubstringInWraproundString(string p) {
        vector<int> DP(26, 0);
        int k=1;
        for(int i=0;i<p.length();i++){
            if(i>0&&isContinue(p[i-1], p[i])){
                k++;
            }else k=1;
            DP[p[i]-'a'] = max(DP[p[i]-'a'], k);
        }
        int ans=0;
        for(int x:DP) ans+=x;
        return ans;
    }
};

1048. 最长字符串链

Description
给出一个单词列表，其中每个单词都由小写英文字母组成。
如果我们可以在 word1 的任何地方添加一个字母使其变成 word2，那么我们认为 word1 是 word2 的前身。例如，”abc” 是 “abac” 的前身。
词链是单词 [word_1, word_2, …, word_k] 组成的序列，k >= 1，其中 word_1 是 word_2 的前身，word_2 是 word_3 的前身，依此类推。
从给定单词列表 words 中选择单词组成词链，返回词链的最长可能长度。
Example
示例：
输入：[“a”,”b”,”ba”,”bca”,”bda”,”bdca”]
输出：4
解释：最长单词链之一为 “a”,”ba”,”bda”,”bdca”。

提示：
1 <= words.length <= 1000
1 <= words[i].length <= 16
words[i] 仅由小写英文字母组成。
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int longestStrChain(vector<string>& words) {
        int n=words.size();
        sort(words.begin(), words.end(), [](string a, string b){return a.length()<b.length();});//按长度排序，注意默认排序是字典序排序，例如"abcde"在"abdde"之前
        int DP[n];
        fill(DP, DP+n, 1);
        int ans=1;
        for(int i=0;i<n;i++){
            for(int j=0;j<i;j++){
                if(words[j].length()!=words[i].length()-1) continue;
                for(int k=0;k<words[i].length();k++){
                    string s=words[i];
                    string str=s.erase(k, 1);
                    if(str==words[j]){
                        DP[i]=max(DP[i],DP[j]+1);
                        ans=max(ans, DP[i]);
                        break;
                    }
                }
            }
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int longestStrChain(vector<string>& words) {
        int n=words.size();
        unordered_map<string, int> DP;
        for(string str:words) DP[str]=1;
        sort(words.begin(), words.end(), [](string a, string b){return a.length()<b.length();});//按长度排序，注意默认排序是字典序排序，例如"abcde"在"abdde"之前
        int ans=1;
        for(int i=0;i<n;i++){
            for(int j=0;j<words[i].size();j++){
                string s=words[i];
                string ss=s.erase(j, 1);
                if(DP.find(ss)!=DP.end()){
                    DP[words[i]]=max(DP[words[i]], DP[ss]+1);
                    ans=max(ans, DP[words[i]]);
                    break;
                }
            }
        }
        return ans;
    }
};

股票系列

121. 买卖股票的最佳时机

Description
给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。
注意你不能在买入股票前卖出股票。
Example
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

示例 2:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int minPrice=INT_MAX;
        int maxProfit=0;
        for(int i=0;i<prices.size();i++){
            if(prices[i]<minPrice){
                minPrice=prices[i];
            }
            maxProfit=max(maxProfit, prices[i]-minPrice);
        }
        return maxProfit;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if(prices.size()==0) return 0;
        int n=prices.size();
        int** DP=new int*[n];
        for(int i=0;i<n;i++) DP[i]=new int[2];
        for(int i=0;i<n;i++){
            if(i-1<0){
                DP[i][0]=0;
                DP[i][1]=-prices[i];
                continue;
            }
            DP[i][0]=max(DP[i-1][0], DP[i-1][1]+prices[i]);
            DP[i][1]=max(DP[i-1][1], -prices[i]);
        }
        return DP[n-1][0];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if(prices.size()==0) return 0;
        int n=prices.size();
        int dp_i_0=0,dp_i_1=-INT_MAX;
        for(int i=0;i<n;i++){
           dp_i_0=max(dp_i_0, dp_i_1+prices[i]);
           dp_i_1=max(dp_i_1, -prices[i]);
        }
        return dp_i_0;
    }
};

122. 买卖股票的最佳时机 II

Description
给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
Example
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
Program

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int result=0;
        for(int i=1;i<prices.size();i++){
            result+=max(0, prices[i]-prices[i-1]);
        }
        return result;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if(prices.size()==0) return 0;
        int n=prices.size();
        int** DP=new int*[n];
        for(int i=0;i<n;i++) DP[i]=new int[2];
        for(int i=0;i<n;i++){
            if(i-1<0){
                DP[i][0]=0;
                DP[i][1]=-prices[i];
                continue;
            }
            DP[i][0]=max(DP[i-1][0], DP[i-1][1]+prices[i]);
            DP[i][1]=max(DP[i-1][1], DP[i-1][0]-prices[i]);
        }
        return DP[n-1][0];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if(prices.size()==0) return 0;
        int n=prices.size();
        int dp_i_0=0, dp_i_1=-INT_MAX;
        for(int i=0;i<n;i++){
            int temp=dp_i_0;
            dp_i_0=max(dp_i_0, dp_i_1+prices[i]);
            dp_i_1=max(dp_i_1, temp-prices[i]);
        }
        return dp_i_0;
    }
};

123. 买卖股票的最佳时机 III

Description
给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
Example
示例 1:
输入: [3,3,5,0,0,3,1,4]
输出: 6
解释: 在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。
随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3 。

示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这个情况下, 没有交易完成, 所以最大利润为 0。
Progam
注意：最多两次交易！可能一次！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if(prices.size()==0) return 0;
        int n=prices.size();
        int*** DP=new int**[n];
        for(int i=0;i<n;i++){
            DP[i]=new int*[3];
            for(int j=0;j<3;j++) DP[i][j]=new int[2];
        }
        for(int i=0;i<n;i++){
            for(int j=0;j<3;j++){
                if(i==0){
                    DP[i][j][0]=0;
                    DP[i][j][1]=-INT_MAX;
                    if(j==1)DP[i][j][1]=-prices[i];
                    continue;
                }

                if(j==0){
                    DP[i][j][0]=0;
                    DP[i][j][1]=-INT_MAX;
                    continue;
                }
                DP[i][j][0]=max(DP[i-1][j][0], DP[i-1][j][1]+prices[i]);
                DP[i][j][1]=max(DP[i-1][j][1], DP[i-1][j-1][0]-prices[i]);
            }
        }
        return max(DP[n-1][1][0],DP[n-1][2][0]);
    }
};

188. 买卖股票的最佳时机 IV

Description
给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一
注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
Example
示例 1:
输入: [2,4,1], k = 2
输出: 2
解释: 在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

示例 2:
输入: [3,2,6,5,0,3], k = 2
输出: 7
解释: 在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
public:
    int maxProfit_inf(vector<int>& prices) {
        if(prices.size()==0) return 0;
        int n=prices.size();
        int dp_i_0=0, dp_i_1=-INT_MAX;
        for(int i=0;i<n;i++){
            int temp=dp_i_0;
            dp_i_0=max(dp_i_0, dp_i_1+prices[i]);
            dp_i_1=max(dp_i_1, temp-prices[i]);
        }
        return dp_i_0;
    }
    int maxProfit(int k, vector<int>& prices) {
        if(prices.size()==0) return 0;
        int n=prices.size();
        if(k>n/2){
            return maxProfit_inf(prices);
        }
        int*** DP=new int**[n];
        for(int i=0;i<n;i++){
            DP[i]=new int*[k+1];
            for(int j=0;j<k+1;j++) DP[i][j]=new int[2];
        }
        int result=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<k+1;j++){
                if(i==0){
                    DP[i][j][0]=0;
                    DP[i][j][1]=-INT_MAX;
                    if(j==1) DP[i][j][1]=-prices[i];
                    continue;
                }
                if(j==0){
                    DP[i][j][0]=0;
                    DP[i][j][1]=-INT_MAX;
                    continue;
                }
                DP[i][j][0]=max(DP[i-1][j][0], DP[i-1][j][1]+prices[i]);
                DP[i][j][1]=max(DP[i-1][j][1], DP[i-1][j-1][0]-prices[i]);
            }
        }
        for(int j=1;j<k+1;j++){
            result=max(result, DP[n-1][j][0]);
        }
        return result;
    }
};

买卖股票问题通解
很多读者抱怨股票系列问题奇技淫巧太多，如果面试真的遇到这类问题，基本不会想到那些巧妙的办法，怎么办？所以本文拒绝奇技淫巧，而是稳扎稳打，只用一种通用方法解决所用问题，以不变应万变。
这篇文章用状态机的技巧来解决，可以全部提交通过。不要觉得这个名词高大上，文学词汇而已，实际上就是 DP table，看一眼就明白了。
先随便抽出一道题，看看别人的解法：

1
2
3
4
5
6
7
8
9
10
11
12
int maxProfit(vector<int>& prices) {
    if(prices.empty()) return 0;
    int s1=-prices[0],s2=INT_MIN,s3=INT_MIN,s4=INT_MIN;

    for(int i=1;i<prices.size();++i) {            
        s1 = max(s1, -prices[i]);
        s2 = max(s2, s1+prices[i]);
        s3 = max(s3, s2-prices[i]);
        s4 = max(s4, s3+prices[i]);
    }
    return max(0,s4);
}

能看懂吧？会做了吗？不可能的，你看不懂，这才正常。就算你勉强看懂了，下一个问题你还是做不出来。为什么别人能写出这么诡异却又高效的解法呢？因为这类问题是有框架的，但是人家不会告诉你的，因为一旦告诉你，你五分钟就学会了，该算法题就不再神秘，变得不堪一击了。

本文就来告诉你这个框架，然后带着你一道一道秒杀。
这 6 道股票买卖问题是有共性的，我们通过对第四题（限制最大交易次数为 k）的分析一道一道解决。因为第四题是一个最泛化的形式，其他的问题都是这个形式的简化。
第一题是只进行一次交易，相当于 k = 1；第二题是不限交易次数，相当于 k = +infinity（正无穷）；第三题是只进行 2 次交易，相当于 k = 2；剩下两道也是不限次数，但是加了交易「冷冻期」和「手续费」的额外条件，其实就是第二题的变种，都很容易处理。
一、穷举框架
首先，还是一样的思路：如何穷举？这里的穷举思路和上篇文章递归的思想不太一样。
递归其实是符合我们思考的逻辑的，一步步推进，遇到无法解决的就丢给递归，一不小心就做出来了，可读性还很好。缺点就是一旦出错，你也不容易找到错误出现的原因。比如上篇文章的递归解法，肯定还有计算冗余，但确实不容易找到。
而这里，我们不用递归思想进行穷举，而是利用「状态」进行穷举。我们具体到每一天，看看总共有几种可能的「状态」，再找出每个「状态」对应的「选择」。我们要穷举所有「状态」，穷举的目的是根据对应的「选择」更新状态。听起来抽象，你只要记住「状态」和「选择」两个词就行，下面实操一下就很容易明白了。

1
2
3
4
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 择优(选择1，选择2...)

比如说这个问题，每天都有三种「选择」：买入、卖出、无操作，我们用 buy, sell, rest 表示这三种选择。但问题是，并不是每天都可以任意选择这三种选择的，因为 sell 必须在 buy 之后，buy 必须在 sell 之后。那么 rest 操作还应该分两种状态，一种是 buy 之后的 rest（持有了股票），一种是 sell 之后的 rest（没有持有股票）。而且别忘了，我们还有交易次数 k 的限制，就是说你 buy 还只能在 k > 0 的前提下操作。

很复杂对吧，不要怕，我们现在的目的只是穷举，你有再多的状态，老夫要做的就是一把梭全部列举出来。这个问题的「状态」有三个，第一个是天数，第二个是允许交易的最大次数，第三个是当前的持有状态（即之前说的 rest 的状态，我们不妨用 1 表示持有，0 表示没有持有）。然后我们用一个三维数组就可以装下这几种状态的全部组合：
dp[i][k][0 or 1]
0 <= i <= n-1, 1 <= k <= K
n 为天数，大 K 为最多交易数
此问题共 n × K × 2 种状态，全部穷举就能搞定。

1
2
3
4
for 0 <= i < n:
    for 1 <= k <= K:
        for s in {0, 1}:
            dp[i][k][s] = max(buy, sell, rest)

而且我们可以用自然语言描述出每一个状态的含义，比如说 dp[3][2][1] 的含义就是：今天是第三天，我现在手上持有着股票，至今最多进行 2 次交易。再比如 dp[2][3][0] 的含义：今天是第二天，我现在手上没有持有股票，至今最多进行 3 次交易。很容易理解，对吧？
我们想求的最终答案是 dp[n - 1][K][0]，即最后一天，最多允许 K 次交易，最多获得多少利润。读者可能问为什么不是 dp[n - 1][K][1]？因为 [1] 代表手上还持有股票，[0] 表示手上的股票已经卖出去了，很显然后者得到的利润一定大于前者。
记住如何解释「状态」，一旦你觉得哪里不好理解，把它翻译成自然语言就容易理解了。
二、状态转移框架
现在，我们完成了「状态」的穷举，我们开始思考每种「状态」有哪些「选择」，应该如何更新「状态」。只看「持有状态」，可以画个状态转移图。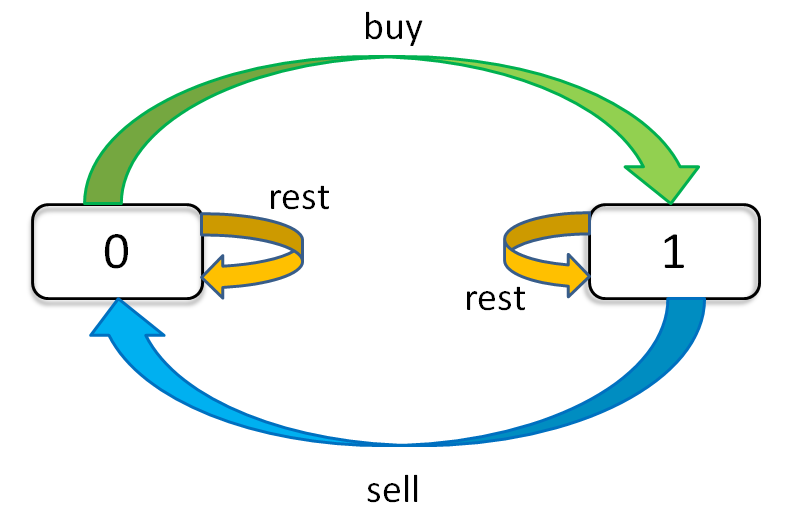
image
通过这个图可以很清楚地看到，每种状态（0 和 1）是如何转移而来的。根据这个图，我们来写一下状态转移方程：

1
2
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
              = max(   选择 rest  ,           选择 sell      )

解释：今天我没有持有股票，有两种可能：
要么是我昨天就没有持有，然后今天选择 rest，所以我今天还是没有持有；
要么是我昨天持有股票，但是今天我 sell 了，所以我今天没有持有股票了。

1
2
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
              = max(   选择 rest  ,           选择 buy         )

解释：今天我持有着股票，有两种可能：
要么我昨天就持有着股票，然后今天选择 rest，所以我今天还持有着股票；
要么我昨天本没有持有，但今天我选择 buy，所以今天我就持有股票了。
这个解释应该很清楚了，如果 buy，就要从利润中减去 prices[i]，如果 sell，就要给利润增加 prices[i]。今天的最大利润就是这两种可能选择中较大的那个。而且注意 k 的限制，我们在选择 buy 的时候，把 k 减小了 1，很好理解吧，当然你也可以在 sell 的时候减 1，一样的。
现在，我们已经完成了动态规划中最困难的一步：状态转移方程。如果之前的内容你都可以理解，那么你已经可以秒杀所有问题了，只要套这个框架就行了。不过还差最后一点点，就是定义 base case，即最简单的情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
dp[-1][k][0] = 0
解释：因为 i 是从 0 开始的，所以 i = -1 意味着还没有开始，这时候的利润当然是 0 。
dp[-1][k][1] = -infinity
解释：还没开始的时候，是不可能持有股票的，用负无穷表示这种不可能。
dp[i][0][0] = 0
解释：因为 k 是从 1 开始的，所以 k = 0 意味着根本不允许交易，这时候利润当然是 0 。
dp[i][0][1] = -infinity
解释：不允许交易的情况下，是不可能持有股票的，用负无穷表示这种不可能。
把上面的状态转移方程总结一下：

base case：
dp[-1][k][0] = dp[i][0][0] = 0
dp[-1][k][1] = dp[i][0][1] = -infinity

状态转移方程：
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
读者可能会问，这个数组索引是 -1 怎么编程表示出来呢，负无穷怎么表示呢？这都是细节问题，有很多方法实现。现在完整的框架已经完成，下面开始具体化。

三、秒杀题目
第一题，k = 1
直接套状态转移方程，根据 base case，可以做一些化简：

1
2
dp[i][1][1] = max(dp[i-1][1][1], dp[i-1][0][0] - prices[i])
            = max(dp[i-1][1][1], -prices[i])

解释：k = 0 的 base case，所以 dp[i-1][0][0] = 0。
现在发现 k 都是 1，不会改变，即 k 对状态转移已经没有影响了。
可以进行进一步化简去掉所有 k：

1
2
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], -prices[i])

直接写出代码：

1
2
3
4
5
6
7
int n = prices.length;
int[][] dp = new int[n][2];
for (int i = 0; i < n; i++) {
    dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
    dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
}
return dp[n - 1][0];

显然 i = 0 时 dp[i-1] 是不合法的。这是因为我们没有对 i 的 base case 进行处理。可以这样处理：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
for (int i = 0; i < n; i++) {
    if (i - 1 == -1) {
        dp[i][0] = 0;
        // 解释：
        //   dp[i][0]
        // = max(dp[-1][0], dp[-1][1] + prices[i])
        // = max(0, -infinity + prices[i]) = 0
        dp[i][1] = -prices[i];
        //解释：
        //   dp[i][1]
        // = max(dp[-1][1], dp[-1][0] - prices[i])
        // = max(-infinity, 0 - prices[i])
        // = -prices[i]
        continue;
    }
    dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
    dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
}
return dp[n - 1][0];

第一题就解决了，但是这样处理 base case 很麻烦，而且注意一下状态转移方程，新状态只和相邻的一个状态有关，其实不用整个 dp 数组，只需要一个变量储存相邻的那个状态就足够了，这样可以把空间复杂度降到 O(1):

1
2
3
4
5
6
7
8
9
10
11
12
13
// k == 1
int maxProfit_k_1(int[] prices) {
    int n = prices.length;
    // base case: dp[-1][0] = 0, dp[-1][1] = -infinity
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        // dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        // dp[i][1] = max(dp[i-1][1], -prices[i])
        dp_i_1 = Math.max(dp_i_1, -prices[i]);
    }
    return dp_i_0;
}

两种方式都是一样的，不过这种编程方法简洁很多。但是如果没有前面状态转移方程的引导，是肯定看不懂的。后续的题目，我主要写这种空间复杂度 O(1) 的解法。

第二题，k = +infinity

如果 k 为正无穷，那么就可以认为 k 和 k - 1 是一样的。可以这样改写框架：

1
2
3
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
            = max(dp[i-1][k][1], dp[i-1][k][0] - prices[i])

我们发现数组中的 k 已经不会改变了，也就是说不需要记录 k 这个状态了：
$$dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])$$
直接翻译成代码：

1
2
3
4
5
6
7
8
9
10
int maxProfit_k_inf(int[] prices) {
    int n = prices.length;
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        int temp = dp_i_0;
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = Math.max(dp_i_1, temp - prices[i]);
    }
    return dp_i_0;
}

第三题，k = +infinity with cooldown
每次 sell 之后要等一天才能继续交易。只要把这个特点融入上一题的状态转移方程即可：
$$dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])$$
解释：第 i 天选择 buy 的时候，要从 i-2 的状态转移，而不是 i-1 。
翻译成代码：

1
2
3
4
5
6
7
8
9
10
11
12
int maxProfit_with_cool(int[] prices) {
    int n = prices.length;
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
    int dp_pre_0 = 0; // 代表 dp[i-2][0]
    for (int i = 0; i < n; i++) {
        int temp = dp_i_0;
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = Math.max(dp_i_1, dp_pre_0 - prices[i]);
        dp_pre_0 = temp;
    }
    return dp_i_0;
}

第四题，k = +infinity with fee
每次交易要支付手续费，只要把手续费从利润中减去即可。改写方程：

1
2
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i] - fee)

解释：相当于买入股票的价格升高了。
在第一个式子里减也是一样的，相当于卖出股票的价格减小了。
直接翻译成代码：

1
2
3
4
5
6
7
8
9
10
int maxProfit_with_fee(int[] prices, int fee) {
    int n = prices.length;
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        int temp = dp_i_0;
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = Math.max(dp_i_1, temp - prices[i] - fee);
    }
    return dp_i_0;
}

第五题，k = 2
k = 2 和前面题目的情况稍微不同，因为上面的情况都和 k 的关系不太大。要么 k 是正无穷，状态转移和 k 没关系了；要么 k = 1，跟 k = 0 这个 base case 挨得近，最后也没有存在感。
这道题 k = 2 和后面要讲的 k 是任意正整数的情况中，对 k 的处理就凸显出来了。我们直接写代码，边写边分析原因。
原始的动态转移方程，没有可化简的地方

1
2
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])

按照之前的代码，我们可能想当然这样写代码（错误的）：

1
2
3
4
5
6
7
8
int k = 2;
int[][][] dp = new int[n][k + 1][2];
for (int i = 0; i < n; i++)
    if (i - 1 == -1) { /* 处理一下 base case*/ }
    dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
    dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
}
return dp[n - 1][k][0];

为什么错误？我这不是照着状态转移方程写的吗？

还记得前面总结的「穷举框架」吗？就是说我们必须穷举所有状态。其实我们之前的解法，都在穷举所有状态，只是之前的题目中 k 都被化简掉了。这道题由于没有消掉 k 的影响，所以必须要对 k 进行穷举：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int max_k = 2;
int[][][] dp = new int[n][max_k + 1][2];
for (int i = 0; i < n; i++) {
    for (int k = max_k; k >= 1; k--) {
        if (i - 1 == -1) { /*处理 base case */ }
        dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
        dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
    }
}
// 穷举了 n × max_k × 2 个状态，正确。
return dp[n - 1][max_k][0];
···
如果你不理解，可以返回第一点「穷举框架」重新阅读体会一下。
这里 k 取值范围比较小，所以可以不用 for 循环，直接把 k = 1 和 2 的情况手动列举出来也可以：

dp[i][2][0] = max(dp[i-1][2][0], dp[i-1][2][1] + prices[i])
dp[i][2][1] = max(dp[i-1][2][1], dp[i-1][1][0] - prices[i])
dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])
dp[i][1][1] = max(dp[i-1][1][1], -prices[i])

1
2
3
4
5
6
7
8
9
10
11
12
```cpp
int maxProfit_k_2(int[] prices) {
    int dp_i10 = 0, dp_i11 = Integer.MIN_VALUE;
    int dp_i20 = 0, dp_i21 = Integer.MIN_VALUE;
    for (int price : prices) {
        dp_i20 = Math.max(dp_i20, dp_i21 + price);
        dp_i21 = Math.max(dp_i21, dp_i10 - price);
        dp_i10 = Math.max(dp_i10, dp_i11 + price);
        dp_i11 = Math.max(dp_i11, -price);
    }
    return dp_i20;
}

有状态转移方程和含义明确的变量名指导，相信你很容易看懂。其实我们可以故弄玄虚，把上述四个变量换成 a, b, c, d。这样当别人看到你的代码时就会一头雾水，大惊失色，不得不对你肃然起敬。
第六题，k = any integer
有了上一题 k = 2 的铺垫，这题应该和上一题的第一个解法没啥区别。但是出现了一个超内存的错误，原来是传入的 k 值会非常大，dp 数组太大了。现在想想，交易次数 k 最多有多大呢？
一次交易由买入和卖出构成，至少需要两天。所以说有效的限制 k 应该不超过 n/2，如果超过，就没有约束作用了，相当于 k = +infinity。这种情况是之前解决过的。
直接把之前的代码重用：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int maxProfit_k_any(int max_k, int[] prices) {
    int n = prices.length;
    if (max_k > n / 2)
        return maxProfit_k_inf(prices);

    int[][][] dp = new int[n][max_k + 1][2];
    for (int i = 0; i < n; i++)
        for (int k = max_k; k >= 1; k--) {
            if (i - 1 == -1) { /* 处理 base case */ }
            dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
            dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);     
        }
    return dp[n - 1][max_k][0];
}

至此，6 道题目通过一个状态转移方程全部解决。
四、最后总结
本文给大家讲了如何通过状态转移的方法解决复杂的问题，用一个状态转移方程秒杀了 6 道股票买卖问题，现在想想，其实也不算难对吧？这已经属于动态规划问题中较困难的了。
关键就在于列举出所有可能的「状态」，然后想想怎么穷举更新这些「状态」。一般用一个多维 dp 数组储存这些状态，从 base case 开始向后推进，推进到最后的状态，就是我们想要的答案。想想这个过程，你是不是有点理解「动态规划」这个名词的意义了呢？
具体到股票买卖问题，我们发现了三个状态，使用了一个三维数组，无非还是穷举 + 更新，不过我们可以说的高大上一点，这叫「三维 DP」，怕不怕？这个大实话一说，立刻显得你高人一等，名利双收有没有。
所以，大家不要被各种高大上的名词吓到，再多的困难问题，奇技淫巧，也不过是基本套路的不断升级组合产生的。只要把住算法的底层原理，即可举一反三，逐个击破。
买卖股票的最佳时机
买卖股票的最佳时机 II
买卖股票的最佳时机 III
买卖股票的最佳时机 IV
最佳买卖股票时机含冷冻期
买卖股票的最佳时机含手续费

309. 最佳买卖股票时机含冷冻期

Description
给定一个整数数组，其中第 i 个元素代表了第 i 天的股票价格 。​
设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:
你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。
Example
示例:
输入: [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if(prices.size()==0) return 0;
        int n=prices.size();
        int** DP=new int*[n];
        for(int i=0;i<n;i++) DP[i]=new int[2];
        for(int i=0;i<n;i++){
            if(i==0){
                DP[i][0]=0;
                DP[i][1]=-prices[i];
                continue;
            }
            if(i==1){
                DP[i][0]=max(DP[i-1][0], DP[i-1][1]+prices[i]);
                DP[i][1]=max(DP[i-1][1], -prices[i]);
                continue;
            }
            DP[i][0]=max(DP[i-1][0], DP[i-1][1]+prices[i]);
            DP[i][1]=max(DP[i-1][1], DP[i-2][0]-prices[i]);
        }
        return DP[n-1][0];
    }
};

714. 买卖股票的最佳时机含手续费

Description
给定一个整数数组 prices，其中第 i 个元素代表了第 i 天的股票价格 ；非负整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易，但是你每次交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
Example
示例 1:
输入: prices = [1, 3, 2, 8, 4, 9], fee = 2
输出: 8
解释: 能够达到的最大利润:
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8.
注意:

1
2
3
0 < prices.length <= 50000.
0 < prices[i] < 50000.
0 <= fee < 50000.

Progam

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        if(prices.size()==0) return 0;
        int n=prices.size();
        int** DP=new int*[n];
        for(int i=0;i<n;i++) DP[i]=new int[2];
        for(int i=0;i<n;i++){
            if(i==0){
                DP[i][0]=0;
                DP[i][1]=-prices[i]-fee;
                continue;
            }
            DP[i][0]=max(DP[i-1][0], DP[i-1][1]+prices[i]);
            DP[i][1]=max(DP[i-1][1], DP[i-1][0]-prices[i]-fee);
        }
        return DP[n-1][0];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        if(prices.size()==0) return 0;
        int n=prices.size();
        int dp_i_0, dp_i_1;
        for(int i=0;i<n;i++){
            if(i==0){
                dp_i_0=0;
                dp_i_1=-prices[i]-fee;
                continue;
            }
            int tmp=dp_i_0;
            dp_i_0=max(dp_i_0, dp_i_1+prices[i]);
            dp_i_1=max(dp_i_1, tmp-prices[i]-fee);
        }
        return dp_i_0;
    }
};

剑指 Offer 63. 股票的最大利润

Description
假设把某股票的价格按照时间先后顺序存储在数组中，请问买卖该股票一次可能获得的最大利润是多少？
Example
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

示例 2:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

限制：
0 <= 数组长度 <= 10^5
Program
动规
画出价格折线图，找出当前最低价格，求差值最大即可

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if(prices.size()==0) return 0;
        int n=prices.size();
        int minPrice=INT_MAX, ans=-INT_MAX;
        for(int i=0;i<n;i++){
            minPrice=min(minPrice, prices[i]);
            ans=max(ans, prices[i]-minPrice);
        }
        return ans;
    }
};

面试题 17.16. 按摩师

Description
一个有名的按摩师会收到源源不断的预约请求，每个预约都可以选择接或不接。在每次预约服务之间要有休息时间，因此她不能接受相邻的预约。给定一个预约请求序列，替按摩师找到最优的预约集合（总预约时间最长），返回总的分钟数。

注意：本题相对原题稍作改动
Example
示例 1：
输入： [1,2,3,1]
输出： 4
解释： 选择 1 号预约和 3 号预约，总时长 = 1 + 3 = 4。

示例 2：
输入： [2,7,9,3,1]
输出： 12
解释： 选择 1 号预约、 3 号预约和 5 号预约，总时长 = 2 + 9 + 1 = 12。

示例 3：
输入： [2,1,4,5,3,1,1,3]
输出： 12
解释： 选择 1 号预约、 3 号预约、 5 号预约和 8 号预约，总时长 = 2 + 4 + 3 + 3 = 12。
Program
思路
设DP[i][0]为不接第i个预约，DP[i][1]为接第i个预约，状态转移方程：
$DP[i][0]=max(DP[i-1][0],DP[i-1][1])$
$DP[i][1]=D[i-1][0]+nums[i]$
时间复杂度：$O(n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    const int inf=0x3f3f3f3f;
    int massage(vector<int>& nums) {
        if(nums.size()==0) return 0;
        int n=nums.size();
        int DP[n][2];
        memset(DP, inf ,sizeof(DP));
        for(int i=0;i<n;i++){
            DP[i][0]=(i>0)?max(DP[i-1][0],DP[i-1][1]):0;
            DP[i][1]=(i>0?DP[i-1][0]:0)+nums[i];
        }
        return max(DP[n-1][0], DP[n-1][1]);
    }
};

丑数系列

264. 丑数 II

Description
编写一个程序，找出第 n 个丑数。
丑数就是只包含质因数 2, 3, 5 的正整数。
Example
示例:
输入: n = 10
输出: 12
解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。
说明:
1 是丑数。
n 不超过1690。
Program
丑数：$X=2^m3^n5^t$，所以先整除2，余数整除3，最后余数整除5，如果整除结果为1，则为丑数；反之不是。
从DP[0]开始，每个数都必须乘以2,3,5各一次加入DP数组，问题使从小到大插入，所以每次去三个乘积最小的结果加入DP数组，那么必然存在重复计算，没得办法，问题在于比如DP[0] * 2在第一次三乘积最小，DP[0]后续不用乘以2了，所以2的指针后移，而3和5的指针还是指向DP[0]，所以三指针！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int nthUglyNumber(int n) {
        vector<int> DP(n,0);
        DP[0]=1;
        int p2, p3, p5;
        p2=p3=p5=0;
        for(int i=1;i<n;i++){
            int mVal=min(DP[p2]*2, min(DP[p3]*3, DP[p5]*5));
            if(mVal==DP[p2]*2) p2++;
            if(mVal==DP[p3]*3) p3++;
            if(mVal==DP[p5]*5) p5++;
            DP[i]=mVal;
        }
        return DP[n-1];
    }
};

313. 超级丑数

Description
编写一段程序来查找第 n 个超级丑数。
超级丑数是指其所有质因数都是长度为 k 的质数列表 primes 中的正整数。
Example
示例:
输入: n = 12, primes = [2,7,13,19]
输出: 32
解释: 给定长度为 4 的质数列表 primes = [2,7,13,19]，前 12 个超级丑数序列为：[1,2,4,7,8,13,14,16,19,26,28,32] 。
说明:
1 是任何给定 primes 的超级丑数。
给定 primes 中的数字以升序排列。
0 < k ≤ 100, 0 < n ≤ 106, 0 < primes[i] < 1000 。
第 n 个超级丑数确保在 32 位有符整数范围内。
Program
堆
与之前的丑数II类似，不同的这里是一组素数
这里根据标签堆的做法；
此版本效率不高

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    struct Node{
        int val;
        int idx;
        Node(int _val, int _idx):val(_val), idx(_idx){}
        bool operator < (const Node& other) const{
            return val>other.val;
        }
    };
    int nthSuperUglyNumber(int n, vector<int>& primes) {
        int k=primes.size();
        vector<int> index(k, 0);
        vector<int> res(n, -1);
        res[0]=1;
        for(int i=1;i<n;i++){
            priority_queue<Node> pq;
            for(int j=0;j<k;j++){
                pq.push(Node(primes[j]*res[index[j]], j)); //入堆
            }  
            Node node=pq.top();
            res[i]=node.val;
            index[node.idx]++;
            for(int j=0;j<k;j++){
                if(primes[j]*res[index[j]]==node.val) index[j]++; //已选出当前最小值res[i]，如果其他primes[j]*res[index[j]]为res[i]，则会出现重复，故后移
            }
        }
        return res[n-1];
    }
};

直接数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    const int inf=INT_MAX;
    int nthSuperUglyNumber(int n, vector<int>& primes) {
        int k=primes.size();
        vector<int> index(k, 0);
        vector<int> res(n, inf);
        res[0]=1;
        for(int i=1;i<n;i++){
            for(int j=0;j<k;j++) res[i]=min(res[i], primes[j]*res[index[j]]);
            for(int j=0;j<k;j++){
                if(primes[j]*res[index[j]]==res[i]) index[j]++; //已选出当前最小值res[i]，如果其他primes[j]*res[index[j]]为res[i]，则会出现重复，故后移
            }
        }
        return res[n-1];
    }
};

343. 整数拆分

Description
给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
Example
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
说明: 你可以假设 n 不小于 2 且不大于 58。
Program
i>3时，DP[i]>=i，递推公式DP[i]=max(DP[i], DP[j]*(i-j))，但是注意到题目要求至少两个正整数之和，那么主要到1~3这三个数题目所求乘积小于自身，那么后面比这几个数大的数，在运用这个递推公式的时候回出现问题，所以要特判！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int integerBreak(int n) {
        vector<int> DP(n+1, 0);
        DP[1]=1;
        for(int i=2;i<n+1;i++){
            for(int j=1;j<i;j++){
                int x=(j<=3)?j:DP[j];
                DP[i]=max(DP[i], x*(i-j));
            }
        }
        return DP[n];
    }
};

见面试题14-I题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int integerBreak(int n) {
        if(n<=3) return n-1;
        int mod=3;
        int res=n%mod;
        int count=n/mod;
        int ans=0;
        if(res==2) ans=(int)pow(mod,count)*2;
        else if(res==1) ans=(int)pow(mod, count-1)*4;
        else ans=(int)pow(mod, count);
        return ans;
    }
};

面试题14- I. 剪绳子

Description
给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。
*Example**
示例 1：
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

提示：
2 <= n <= 58
Program
image
image
image

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int cuttingRope(int n) {
        if(n<=3) return n-1;
        int mod=3;
        int res=n%mod;
        int count=n/mod;
        int ans=0;
        if(res==2) ans=(int)pow(mod,count)*2;
        else if(res==1) ans=(int)pow(mod, count-1)*4;
        else ans=(int)pow(mod, count);
        return ans;
    }
};

面试题14- II. 剪绳子 II

Description
给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]…k[m] 。请问 $k[0] * k[1] * … * k[m]$ 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。
答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。
Example
示例 1：
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

提示：
2 <= n <= 1000
Program
动态规划不行，数值太大了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    const int MOD=1e9+7;
    int cal(int mod, int count, int res){
        long long ans=1;
        if(res==1) count--;
        while(count>0){
            ans=ans*mod%MOD;count--;
        }
        if(res==1) ans=ans*4%MOD;
        if(res==2) ans=ans*2%MOD;
        return ans;
    }
    int cuttingRope(int n) {
        if(n<=3) return n-1;
        int mod=3;
        int res=n%mod;
        int count=n/mod;
        int ans=0;
        if(res==2) ans=cal(mod, count, res);
        else if(res==1) ans=cal(mod, count, res);
        else ans=cal(mod, count, res);
        return ans;
    }
};

优化DP

5631. 跳跃游戏 VI

Description
给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。
一开始你在下标 0 处。每一步，你最多可以往前跳 k 步，但你不能跳出数组的边界。也就是说，你可以从下标 i 跳到 [i + 1， min(n - 1, i + k)] 包含 两个端点的任意位置。
你的目标是到达数组最后一个位置（下标为 n - 1 ），你的 得分 为经过的所有数字之和。
请你返回你能得到的 最大得分 。
Example
示例 1：
输入：nums = [1,-1,-2,4,-7,3], k = 2
输出：7
解释：你可以选择子序列 [1,-1,4,3] （上面加粗的数字），和为 7 。

示例 2：
输入：nums = [10,-5,-2,4,0,3], k = 3
输出：17
解释：你可以选择子序列 [10,4,3] （上面加粗数字），和为 17 。

示例 3：
输入：nums = [1,-5,-20,4,-1,3,-6,-3], k = 2
输出：0

提示：
$1 <= nums.length, k <= 10^5$
$-10^4 <= nums[i] <= 10^4$
Program
设DP[i]=max(DP[j])+nums[i]，其中i-k<=j<i，时间复杂度：$O(n^2)$
优化如下
优先队列
max(DP[j])通过优先队列查找，且窗口外的dp值全部抛出
时间复杂度：$O(n\log{n})$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int maxResult(vector<int>& nums, int k) {
        int n=nums.size();
        priority_queue<pair<int,int>> pq;
        pq.push({nums[0], 0});
        int ans=nums[0];
        for(int i=1;i<n;i++){
            while(i-pq.top().second>k) pq.pop(); //超过窗口k的全部剔除
            ans=pq.top().first+nums[i];
            pq.push({ans, i});
        }
        return ans;
    }
};

单调队列
窗口内的dp值保持单调递减，因为对于i-k<=j1,j2<i来说，如果dp[j1]<dp[j2]，那么j1就应当永久剔除，因为不影响后续结果；
时间复杂度：$O(n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int maxResult(vector<int>& nums, int k) {
        int n=nums.size();
        deque<pair<int,int>> q; //单调递减队列，p.first即dp[i]的值单调减
        q.emplace_back(nums[0], 0);
        int ans=nums[0];
        for(int i=1;i<n;i++){
            while(i-q.front().second>k) q.pop_front(); //超过窗口范围
            ans=q.front().first+nums[i];
            while(!q.empty()&&q.back().first<ans) q.pop_back(); //维持单调性
            q.emplace_back(ans, i);
        }
        return ans;
    }
};

其他

279. 完全平方数

Description
给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, …）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
Example
示例 1:
输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.

示例 2:
输入: n = 13
输出: 2
解释: 13 = 4 + 9.
Program
初始化$DP[i]=i$表示最多i个1组成,$DP[i]=min(DP[i], DP[i-jj]+1), if(jj<=i)$为状态转移方程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int numSquares(int n) {
        vector<int> DP(n+1, 0);
        DP[0]=0;
        for(int i=1;i<n+1;i++){
            DP[i]=i;
            for(int j=1;i>=j*j;j++){
                DP[i]=min(DP[i], DP[i-j*j]+1);
            }
        }
        return DP[n];
    }
};

338. 比特位计数

Description
给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ，计算其二进制数中的 1 的数目并将它们作为数组返回。
Example
示例 1:
输入: 2
输出: [0,1,1]

示例 2:
输入: 5
输出: [0,1,1,2,1,2]
进阶:

给出时间复杂度为O(nsizeof(integer))的解答非常容易。但你可以在线性时间O(n)内用一趟扫描做到吗？
要求算法的空间复杂度为O(n)。
你能进一步完善解法吗？要求在C++或任何其他语言中不使用任何内置函数（如 C++ 中的 __builtin_popcount）来执行此操作。
*Program**
位运算+DP
思路类似动态规划
偶数时，比如二进制 1010 其1的个数和它除以2的是一样的，即和 101 带1个数一致
奇数时，加一即可，可以得出
$res[i] = res[i >> 1] + (i & 1)$

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    vector<int> countBits(int num) {
        vector<int> result(num+1, 0);
        for(int i=1;i<=num;i++){
            result[i]=result[i>>1]+(i%2);
        }
        return result;
    }
};

357. 计算各个位数不同的数字个数

Description
给定一个非负整数 n，计算各位数字都不同的数字 x 的个数，其中 $0 ≤ x < 10^n$ 。
Example
示例:
输入: 2
输出: 91
解释: 答案应为除去 11,22,33,44,55,66,77,88,99 外，在 [0,100) 区间内的所有数字。
。
Program
$DP[n]=DP[n-1]+9 * C_9^n * A_n^n=DP[n-1]+9*A_9^{(n-1)};$
区间$[0,10^n)=[0,1)+[1,10)+…+[10^{(n-1)}, 10^n)$，即不同的个数由各x位不同数字个数之和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int countNumbersWithUniqueDigits(int n) {
        vector<int> DP(11);
        DP[0]=1;
        int pre=1;
        for(int i=1;i<=10;i++){
            DP[i]=DP[i-1]+9*pre;
            pre=pre*(10-i);
        }
        if(n<=10) return DP[n];
        else return DP[10];
    }
};

368. 最大整除子集

Description
给出一个由无重复的正整数组成的集合，找出其中最大的整除子集，子集中任意一对 (Si，Sj) 都要满足：Si % Sj = 0 或 Sj % Si = 0。
如果有多个目标子集，返回其中任何一个均可。
Example
示例 1:
输入: [1,2,3]
输出: [1,2] (当然, [1,3] 也正确)

示例 2:
输入: [1,2,4,8]
输出: [1,2,4,8]
Program
思路
（1）取模的性质，如果x能够整除一个整除子集中的最大值，那么其可加入该子集构成新的整除子集；
（2）先对nums排序，设dp[i]为以a[i]为整除子集最大值且为结尾的最大个数；
（3）状态转移方程：dp[i]=max(dp[j])+1
（4）由于需要保留子集结果，则构造结构体存储dp[i]的值以及以a[i]为结尾升序排列的整除子集的前一个元素下标father；
（5）dp后，根据father可以获取整个结果子集！
时间复杂度：$O(n^2)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
public:
    struct Node{
        int father; //以a[i]为结尾升序的整除子集的前一个值的索引
        int ans;  //以a[i]为结尾的整除子集的元素个数
        Node(){}
        Node(int _father, int _ans, int _value){
            father=_father;
            ans=_ans;
        }
    };
    vector<int> largestDivisibleSubset(vector<int>& nums) {
        if(nums.size()==0) return {};
        int n=nums.size();
        sort(nums.begin(), nums.end()); //升序排列，方便后面dp
        vector<Node> dp(n);
        for(int i=0;i<n;i++){ //初始化
            dp[i].father=-1;
            dp[i].ans=1;
        }
        int resCnt=0, resIdx=-1; //最大整除子集元素个数及其索引（尾元素）
        for(int i=0;i<n;i++){  //dp
            for(int j=0;j<i;j++){
                if(nums[i]%nums[j]==0){
                    if(dp[j].ans+1>dp[i].ans){
                        dp[i].ans=dp[j].ans+1;
                        dp[i].father=j;
                    }
                }
            }
            if(resCnt<dp[i].ans){ //更新
                resCnt=dp[i].ans;
                resIdx=i;
            }
        }
        vector<int> res; //计算结果子集
        while(resIdx!=-1){
            res.push_back(nums[resIdx]);
            resIdx=dp[resIdx].father;
        }
        reverse(res.begin(), res.end());
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<int> largestDivisibleSubset(vector<int>& nums) {
        if(nums.size()==0) return {};
        int n=nums.size();
        vector<vector<int>> DP;
        DP.resize(n);
        sort(nums.begin(), nums.end());
        DP[0]=vector<int>(1,nums[0]);

        int idx=0;
        for(int i=1;i<n;i++){
            for(int j=0;j<i;j++){
                int nTmp=DP[j].size();
                int x=DP[j][nTmp-1];
                if(nums[i]%x==0&&nTmp+1>DP[i].size()){
                    vector<int> vec(DP[j].begin(), DP[j].end());
                    vec.push_back(nums[i]);
                    DP[i]=vec;
                    if(DP[idx].size()<DP[i].size()) idx=i;
                }else if(DP[i].size()==0){
                    vector<int> vec(1, nums[i]);
                    DP[i]=vec;
                }
            }
        }
        return DP[idx];
    }
};

376. 摆动序列

Description
如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。少于两个元素的序列也是摆动序列。
例如， [1,7,4,9,2,5] 是一个摆动序列，因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。
给定一个整数序列，返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。
Example
示例 1:
输入: [1,7,4,9,2,5]
输出: 6
解释: 整个序列均为摆动序列。

示例 2:
输入: [1,17,5,10,13,15,10,5,16,8]
输出: 7
解释: 这个序列包含几个长度为 7 摆动序列，其中一个可为[1,17,10,13,10,16,8]。

示例 3:
输入: [1,2,3,4,5,6,7,8,9]
输出: 2
进阶:
你能否用$O(n)$时间复杂度完成此题?
Program
①$DP[i]=max(DP[i], DP[j]+1)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int n=nums.size();
        if(n==0) return 0;
        vector<int>DP(n, 1);
        vector<int> flag(n, 0);
        int result=1;
        for(int i=1;i<n;i++){
            for(int j=0;j<i;j++){
                if(flag[j]>=0&&nums[i]<nums[j]&&DP[i]<DP[j]+1){
                    DP[i]=DP[j]+1;
                    flag[i]=-1;
                }
                if(flag[j]<=0&&nums[i]>nums[j]&&DP[i]<DP[j]+1){
                    DP[i]=DP[j]+1;
                    flag[i]=1;
                }
                result=max(result, DP[i]);
            }
        }
        return result;
    }
};

②令$up[i]$表示以i为结尾的上升摆动序列，$down[i]$表示以i为结尾的下降摆动序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int n=nums.size();
        if(n==0) return 0;
        vector<int> up(n, 0), down(n ,0);
        up[0]=down[0]=1;
        for(int i=1;i<n;i++){
            if(nums[i]>nums[i-1]){
                up[i]=down[i-1]+1;
                down[i]=down[i-1];
            }
            if(nums[i]<nums[i-1]){
                down[i]=up[i-1]+1;
                up[i]=up[i-1];
            }
            if(nums[i]==nums[i-1]){
                down[i]=down[i-1];
                up[i]=up[i-1];
            }
        }
        return max(up[n-1], down[n-1]);
    }
};

③空间优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int n=nums.size();
        if(n==0) return 0;
        int up, down;
        up=down=1;
        for(int i=1;i<n;i++){
            if(nums[i]>nums[i-1]){
                up=down+1;
            }
            if(nums[i]<nums[i-1]){
                down=up+1;
            }
        }
        return max(up, down);
    }
};

413. 等差数列划分

Description
如果一个数列至少有三个元素，并且任意两个相邻元素之差相同，则称该数列为等差数列。
例如，以下数列为等差数列:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
以下数列不是等差数列。
1, 1, 2, 5, 7
数组 A 包含 N 个数，且索引从0开始。数组 A 的一个子数组划分为数组 (P, Q)，P 与 Q 是整数且满足 $0<=P<Q<N$ 。
如果满足以下条件，则称子数组(P, Q)为等差数组：
元素 A[P], A[p + 1], …, A[Q - 1], A[Q] 是等差的。并且 P + 1 < Q 。
函数要返回数组 A 中所有为等差数组的子数组个数。
Example
示例:
A = [1, 2, 3, 4]
返回: 3, A 中有三个子等差数组: [1, 2, 3], [2, 3, 4] 以及自身 [1, 2, 3, 4]。
Program
花里胡哨看不懂题目，题目就是求连续子序列满足等差数列的个数
①暴力

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& A) {
        int n=A.size();
        if(n<3) return 0;
        int ans=0;
        for(int i=0;i+2<n;i++){
            int tmp=0;
            for(int j=i+1;j<n;j++){
                if(j==i+1){
                    tmp=A[j]-A[j-1];
                    continue;
                }
                if(A[j]-A[j-1]!=tmp) break;
                else ans++;
            }
        }
        return ans;
    }
};

②DP
DP[i]表示以i为结尾的等差数列长度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& A) {
        int n=A.size();
        if(n<3) return 0;
        int ans=0;
        vector<int> DP(n, 0);
        for(int i=2;i<n;i++){
            if(DP[i-1]==0){
                if(A[i]-A[i-1]==A[i-1]-A[i-2]) DP[i]=3;
            }else if(A[i]-A[i-1]==A[i-1]-A[i-2]) DP[i]=DP[i-1]+1;
            if(DP[i]>0) ans+=DP[i]-2;
        }
        return ans;
    }
};

DP[i]表示以i为结尾的等差子序列个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& A) {
        int n=A.size();
        if(n<3) return 0;
        int ans=0;
        vector<int> DP(n, 0);
        for(int i=2;i<n;i++){
            if(A[i]-A[i-1]==A[i-1]-A[i-2]) DP[i]=DP[i-1]+1;
            ans+=DP[i];
        }
        return ans;
    }
};

优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& A) {
        int n=A.size();
        if(n<3) return 0;
        int ans=0;
        int dp=0;
        for(int i=2;i<n;i++){
            if(A[i]-A[i-1]==A[i-1]-A[i-2]) dp=dp+1;
            else dp=0;
            ans+=dp;
        }
        return ans;
    }
};

523. 连续的子数组和

Description
给定一个包含非负数的数组和一个目标整数 k，编写一个函数来判断该数组是否含有连续的子数组，其大小至少为 2，总和为 k 的倍数，即总和为 nk，其中 n 也是一个整数。
*Example**
示例 1:
输入: [23,2,4,6,7], k = 6
输出: True
解释: [2,4] 是一个大小为 2 的子数组，并且和为 6。
示例 2:

输入: [23,2,6,4,7], k = 6
输出: True
解释: [23,2,6,4,7]是大小为 5 的子数组，并且和为 42。
说明:
数组的长度不会超过10,000。
你可以认为所有数字总和在 32 位有符号整数范围内。
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    bool checkSubarraySum(vector<int>& nums, int k) {
        if(nums.size()<2) return false;
        int n=nums.size();
        vector<int>DP(n, 0);
        int sum=0;
        for(int i=0;i<n;i++){
            sum+=nums[i];
            DP[i]=sum;
        }
        for(int i=1;i<n;i++){
            if(k==0&&DP[i]==0) return true;
            else if(k!=0&&DP[i]%k==0) return true;
            for(int j=0;j<i-1;j++){
                if(k==0&&(DP[i]-DP[j])==0) return true;
                else if(k!=0&&(DP[i]-DP[j])%k==0) return true;
            }
        }
        return false;
    }
};

用Hash存当前$sum[i]%k$，如果i和j位置的余数$sum[i]%k==sum[j]%k$说明$i+1…j$为所求子数组，因为设i位置和为$m*k+rem$,j位置和为$n*k+rem$，其中$rem=sum[i]%k$，那么$i+1…j$的和为$n*k+rem-m*k-rem=(m-n)*k$！！得证！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    bool checkSubarraySum(vector<int>& nums, int k) {
        if(nums.size()<2) return false;
        int n=nums.size();
        unordered_map<int, int> m; //m[rem]=i
        m[0]=-1; //精髓！i~j为所求子数组！当然要包括第一个数，因为sum%k==0，k==0时也满足
        int sum=0;
        for(int i=0;i<n;i++){
            sum+=nums[i];
            if(k!=0) sum%=k;
            if(m.find(sum)!=m.end()){
                if(i-m[sum]>1) return true; //i和j位置的sum的余数都相同，所以i+1~j为所求子数组
            }else m[sum]=i;
        }
        return false;
    }
};

646. 最长数对链

给出 n 个数对。 在每一个数对中，第一个数字总是比第二个数字小。
现在，我们定义一种跟随关系，当且仅当 b < c 时，数对(c, d) 才可以跟在 (a, b) 后面。我们用这种形式来构造一个数对链。
给定一个对数集合，找出能够形成的最长数对链的长度。你不需要用到所有的数对，你可以以任何顺序选择其中的一些数对来构造。
Example
示例 :
输入: [[1,2], [2,3], [3,4]]
输出: 2
解释: 最长的数对链是 [1,2] -> [3,4]
注意：
给出数对的个数在 [1, 1000] 范围内。
Program
①DP
DP[i]表示以i为结尾的最长数对链个数，DP[i]=max(DP[i], DP[j]+1) if pairs[i][0]>pairs[j][1]，当然这里应当对pairs按照第一元素升序排列。
时间复杂度:$O(N^{2})$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    static bool cmp(vector<int> a, vector<int> b){
        return a[0]<b[0];
    }
    int findLongestChain(vector<vector<int>>& pairs) {
        if(pairs.size()==0) return 0;
        int n=pairs.size();
        sort(pairs.begin(), pairs.end(), cmp);
        vector<int> DP(n, 1);
        int ans=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<i;j++){
                if(pairs[i][0]>pairs[j][1]) DP[i]=max(DP[i], DP[j]+1);
            }
            ans=max(ans, DP[i]);
        }
        return ans;
    }
};

②贪心
将pairs按第二个元素升序排列，贪心的思路就是选择第二个元素较小的数对，之后进行比较，时间复杂度:$O(N\log{N})$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    const int inf=0x3f3f3f3f;
    static bool cmp(vector<int> a, vector<int> b){
        return a[1]<b[1];
    }
    int findLongestChain(vector<vector<int>>& pairs) {
        if(pairs.size()==0) return 0;
        int n=pairs.size();
        sort(pairs.begin(), pairs.end(), cmp);
        vector<int> DP(n, 1);
        int ans=0;
        int cur=-inf;
        for(int i=0;i<n;i++){
            if(cur<pairs[i][0]){
                cur=pairs[i][1];
                ans++;
            }
        }
        return ans;
    }
};

718. 最长重复子数组

Description
给两个整数数组 A 和 B ，返回两个数组中公共的、长度最长的子数组的长度。
Example
示例 1:
输入:
A: [1,2,3,2,1]
B: [3,2,1,4,7]
输出: 3
解释:
长度最长的公共子数组是 [3, 2, 1]。
说明:

1
2
1 <= len(A), len(B) <= 1000
0 <= A[i], B[i] < 100

Program
子数组需要连续，DP[i][j]=DP[i-1][j-1]+1, if A[i]==B[i] else 0.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int findLength(vector<int>& A, vector<int>& B) {
        int m=A.size();
        int n=B.size();
        if(m==0||n==0) return 0;
        vector<vector<int>> DP(m+1, vector<int>(n+1, 0));
        int ans=0;
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(A[i-1]==B[j-1]) DP[i][j]=DP[i-1][j-1]+1;
                ans=max(DP[i][j], ans);
            }
        }
        return ans;
    }
};

740. 删除与获得点数

Description
给定一个整数数组 nums ，你可以对它进行一些操作。
每次操作中，选择任意一个 nums[i] ，删除它并获得 nums[i] 的点数。之后，你必须删除每个等于 nums[i] - 1 或 nums[i] + 1 的元素。
开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。
Example
示例 1:
输入: nums = [3, 4, 2]
输出: 6
解释:
删除 4 来获得 4 个点数，因此 3 也被删除。
之后，删除 2 来获得 2 个点数。总共获得 6 个点数。

示例 2:
输入: nums = [2, 2, 3, 3, 3, 4]
输出: 9
解释:
删除 3 来获得 3 个点数，接着要删除两个 2 和 4 。
之后，再次删除 3 获得 3 个点数，再次删除 3 获得 3 个点数。
总共获得 9 个点数。
注意:
nums的长度最大为20000。
每个整数nums[i]的大小都在[1, 10000]范围内。
Program
①暴力
果断超时

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    unordered_map<int, int> m;
    int ans=0;
    void dfs(vector<int>& nums, int sum){
        if(isEmpty()){
            ans=max(ans, sum);
            return;
        }
        for(int i=0;i<nums.size();i++){
            if(m[nums[i]]!=0){
                int tmp1=m[nums[i]-1];
                int tmp2=m[nums[i]+1];
                m[nums[i]-1]=0;
                m[nums[i]+1]=0;
                m[nums[i]]--;
                dfs(nums, sum+nums[i]);
                m[nums[i]]++;
                m[nums[i]-1]=tmp1;
                m[nums[i]+1]=tmp2;
            }
        }
    }
    bool isEmpty(){
        for(int i=0;i<=10001;i++) if(m[i]!=0) return false;
        return true;
    }
    int deleteAndEarn(vector<int>& nums) {
        for(int i=0;i<=10001;i++) m[i]=0;
        for(int x:nums) m[x]++;
        dfs(nums, 0);
        return ans;
    }
};

打家劫舍DP
设DP[x]为数组[1…x]进行x的选择与否的点数，则DP[x]=max(DP[x-2]+m[x]*x,DP[x-1]);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    unordered_map<int, int> m;
    int deleteAndEarn(vector<int>& nums) {
        if(nums.size()==0) return 0;
        int mx=0;
        for(int x:nums) mx=max(mx, x);
        for(int i=0;i<=mx;i++) m[i]=0;
        for(int x:nums) m[x]++;
        vector<int> DP(mx+1, 0);
        DP[1]=m[1];
        for(int i=2;i<=mx;i++){
            DP[i]=max(DP[i-2]+m[i]*i, DP[i-1]);
        }
        return DP[mx];
    }
};

790. 多米诺和托米诺平铺

Description
有两种形状的瓷砖：一种是 2x1 的多米诺形，另一种是形如 “L” 的托米诺形。两种形状都可以旋转。
XX <- 多米诺
XX <- “L” 托米诺
X
给定 N 的值，有多少种方法可以平铺 2 x N 的面板？返回值 mod 10^9 + 7。
（平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。）
Example
示例:
输入: 3
输出: 5
解释:
下面列出了五种不同的方法，不同字母代表不同瓷砖：
XYZ XXZ XYY XXY XYY
XYZ YYZ XZZ XYY XXY
提示：
N的范围是 [1, 1000]
Program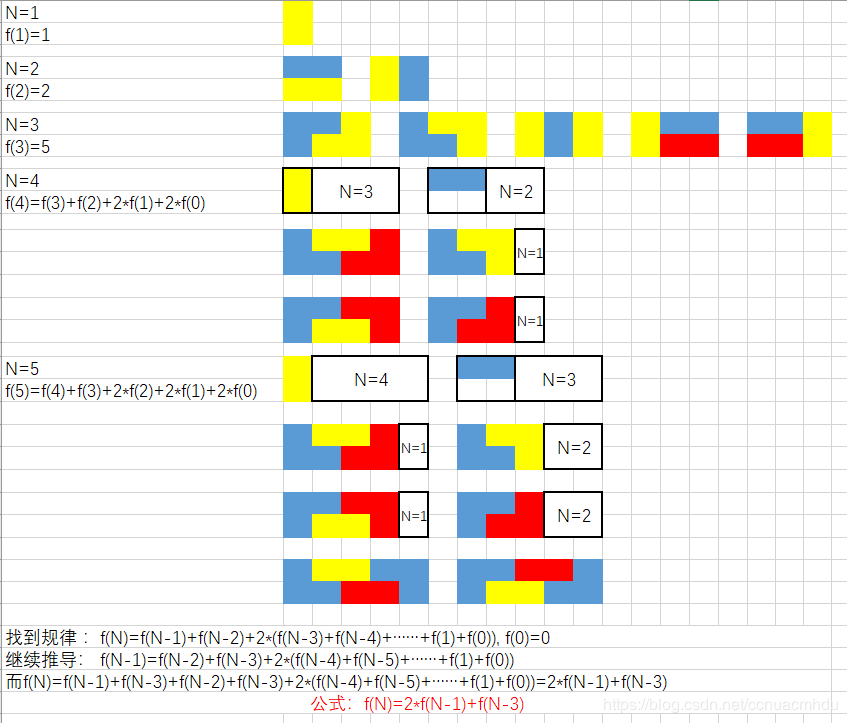
image

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int numTilings(int N) {
        int mod=1e9+7;
        vector<long long> DP(4, 0);
        DP[0]=0;
        DP[1]=1;
        DP[2]=2;
        DP[3]=5;
        DP.resize(N+1);
        for(int i=4;i<=N;i++){
            DP[i]=(DP[i-1]*2%mod+DP[i-3])%mod;
        }
        return DP[N];
    }
};

801. 使序列递增的最小交换次数

Description
我们有两个长度相等且不为空的整型数组 A 和 B 。
我们可以交换 A[i] 和 B[i] 的元素。注意这两个元素在各自的序列中应该处于相同的位置。
在交换过一些元素之后，数组 A 和 B 都应该是严格递增的（数组严格递增的条件仅为A[0] < A[1] < A[2] < … < A[A.length - 1]）。
给定数组 A 和 B ，请返回使得两个数组均保持严格递增状态的最小交换次数。假设给定的输入总是有效的。
Example
示例:
输入: A = [1,3,5,4], B = [1,2,3,7]
输出: 1
解释:
交换 A[3] 和 B[3] 后，两个数组如下:
A = [1, 3, 5, 7] ， B = [1, 2, 3, 4]
两个数组均为严格递增的。
注意:
A, B 两个数组的长度总是相等的，且长度的范围为 [1, 1000]。
A[i], B[i] 均为 [0, 2000]区间内的整数。
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
/**
  * 解题思路：
  * 其实这道题并没有想象中那么难，只是因为题目对的描述有一些地方不到位，导致在求解过程中不能正确理解题意，做不出来。
  * 题目说到，我们*只可以交换两个数组同一个索引位置i*，最终要使得两个数组都呈现递增，随后题目说到假设输入总是有效的
  * 这句话的意思是说，题目的输入总是至少存在一种方法可以使两个数组变成递增数组，不存在如下的数组：
  *
  *  A :  4 3
  *  B :  1 2
  *
  *  上述的输入无论怎么样尝试，按照题目的方法是没办法将其转化成一个两个递增数组的，既然题目说了输入都是有效的那必然是不存在
  *  上面的输入的。
  *
  *  A: a1,a2,a3,a4...an
  *  B: b1.b2.b3,b4...bn
  *
  *  其实我们可以根据上面的描述知道，对于任意一个位置i，必然有A[i] > A[i-1] || A[i] > B[i-1]
  *  可以简单证明一下 如果i位置有A[i] <= A[i-1] && A[i] <= B[i-1]由于我们只能在同一个索引两个数组
  *  对应位置进行交换，那么可以看出A[i] <= A[i-1] && A[i] <= B[i-1]时，无论怎么换在i位置都不能满足
  *  形成递增数组的要求，所以我们之前的假设成立。同理上面的公式对于B也成立，即B[i] > B[i-1] || B[i] > A[i-1]。
  *
  *  组合A,B的情况，合乎题意的无外乎两种 1. A[i] > A[i-1] && B[i] > B[i-1] 2. B[i] > A[i-1] && A[i] > B[i-1]
  *  对于A[i] > A[i-1] && B[i] > A[i-1] 和 A[i] > B[i-1] && B[i] > B[i-1]  都是一个问题 拿第一个举例，
  *  对于B[i-1]的情况我们无从知晓，这就导致了，没法确定一定在交换后可以形成递增序列，而题目又说输入一定是有效的
  *  那无外乎A[i]>A[i-1]>B[i-1] 或者 A[i] > B[i-1] > A[i-1] 而这又退化成了我们列举的两种情况，综上只需要讨论
  *  我们列举的两种情况即可。
  *
  *  对于某个索引i，如果满足A[i] > A[i-1] && B[i] > B[i-1] 就认为在i位置时，是满足递增的要求的。
  *  对于某个索引i，如果满足A[i] > B[i-1] && B[i] > A[i-1] 就认为需要进行交换才可以满足递增的要求。
  *
  *  在考虑时，每一次我们都只需要考虑当前位置是否可以和他的前面一个位置构成严格递增，针对每一个位置如此考虑最终我们会得到一个
  *  整个数组都是严格递增。
  *
  *  在考虑每一个位置时，需要计算当前位置进行交换使当前位置达到递增的代价和不交换达到递增的代价和不交换使当前位置达到递增的代价。
  *
  *  我们在某个位置上可能的序列有两种针对A[i] > A[i - 1] && B[i] > B[i - 1]这种序列
  *  在该位置i上不交换的使得两数组递增的代价为：dp[0][i] = Math.min(dp[0][i], dp[0][i-1])，因为保持就好不用动就已经满足了递增要求
  *  在该位置上交换使得数组递增的代价为dp[1][i] = Math.min(dp[1][i], dp[1][i-1] + 1)，那么需要一起动这样才能保持递增的要求。
  *
  *  对于i位置序列为A[i] > B[i-1] && B[i] > A[i-1]时
  *  如果该位置不交换，使得两数组递增的代价为（思路就是i不换，就让i-1换，换完自然就满足两数组都递增了）dp[0][i] = Math.min(dp[0][i], dp[1][i-1]);
  *  对于i位置交换，使得两数组递增的代价为（思路就是i换，那么i-1就不要动，换完就满足了两数组都递增）：dp[1][i] = Math.min(dp[1][i], dp[0][i-1] + 1)
  *
  *  我们可以看到对于每一个位置都有两种方法使其呈现递增，那么最终的结果就是两者中的最小值。
  */
 public int minSwap(int[] A, int[] B) {
     int len = A.length;
     int[][] dp = new int[2][len];
     for (int inner[] : dp) {
         Arrays.fill(inner, Integer.MAX_VALUE);
     }
     //0 donate A[i-1] not swap 1 donate A[i-1] has swapped
     dp[0][0] = 0;
     dp[1][0] = 1;
     for (int i = 1; i < A.length; i++) {
         if (A[i] > A[i - 1] && B[i] > B[i - 1]) {
             dp[0][i] = Math.min(dp[0][i], dp[0][i-1]);
             dp[1][i] = Math.min(dp[1][i], dp[1][i-1] + 1);
         }

         if(A[i] > B[i-1] && B[i] > A[i-1]){
             dp[0][i] = Math.min(dp[0][i], dp[1][i-1]);
             dp[1][i] = Math.min(dp[1][i], dp[0][i-1] + 1);
         }

     }
     return Math.min(dp[0][len - 1], dp[1][len - 1]);
 }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    const int INF=0x3f3f3f3f;
    int minSwap(vector<int>& A, vector<int>& B) {
        int n=A.size();
        int noChange=0,change=1;
        for(int i=1;i<n;i++){
            int noChange2=INF,change2=INF;
            //两个条件可能同时成立
            if(A[i-1]<A[i]&&B[i-1]<B[i]){
                noChange2=min(noChange, noChange2); //i位置不交换，i-1也不交换
                change2=min(change2, change+1);  //i位置交换，那么i-1必交换
            }
            if(A[i-1]<B[i]&&B[i-1]<A[i]){  
                noChange2=min(noChange2, change); //i位置不交换，那么i-1必交换
                change2=min(change2, noChange+1); //i位置交换，则i-1不交换
            }
            noChange=noChange2;
            change=change2;
        }
        return min(noChange, change);
    }
};

813. 最大平均值和的分组

Description
我们将给定的数组 A 分成 K 个相邻的非空子数组 ，我们的分数由每个子数组内的平均值的总和构成。计算我们所能得到的最大分数是多少。
注意我们必须使用 A 数组中的每一个数进行分组，并且分数不一定需要是整数。
Example
示例:
输入:
A = [9,1,2,3,9]
K = 3
输出: 20
解释:
A 的最优分组是[9], [1, 2, 3], [9]. 得到的分数是 9 + (1 + 2 + 3) / 3 + 9 = 20.
我们也可以把 A 分成[9, 1], [2], [3, 9].
这样的分组得到的分数为 5 + 2 + 6 = 13, 但不是最大值.
说明:
1 <= A.length <= 100.
1 <= A[i] <= 10000.
1 <= K <= A.length.
答案误差在 10^-6 内被视为是正确的。
Program
设DP[i]k为将前i+1个元素分成k部分的最大均值和。
递推公式：$DP[i][k]=max(DP[j-1][k-1]+(preSum[i]-preSum[j-1])/(i-j+1)), j=0,…,i$
i+1<k，DP[i][k]=0，i+1个元素分成k个部分，只有i+1大于等于k时才可能。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    double largestSumOfAverages(vector<int>& A, int K) {
        int n=A.size();
        double DP[n][K+1],preSum[n];
        memset(DP, 0, sizeof(DP));
        memset(preSum, 0, sizeof(preSum));
        for(int i=0;i<n;i++){
            preSum[i]=A[i];
            if(i>0) preSum[i]+=preSum[i-1];
            for(int k=1;k<=K&&k<=i+1;k++){
                if(k==1) {DP[i][k]=preSum[i]/(i+1);continue;} //k==1时，只能全部分给这一份
                for(int j=k-1;j<=i;j++){ //分成k分，那么0~j-1必须能够分成k-1分，即j>=k-1
                    DP[i][k]=max(DP[i][k], (preSum[i]-preSum[j-1])/(i-j+1) + DP[j-1][k-1]);
                }
            }
        }
        return DP[n-1][K];
    }
};

845. 数组中的最长山脉

Description
我们把数组 A 中符合下列属性的任意连续子数组 B 称为 “山脉”：
$B.length >= 3$
存在 $0 < i < B.length - 1$ 使得 $B[0] < B[1] < … B[i-1] < B[i] > B[i+1] > … > B[B.length - 1]$
（注意：B 可以是 A 的任意子数组，包括整个数组 A。）
给出一个整数数组 A，返回最长 “山脉” 的长度。
如果不含有 “山脉” 则返回 0。

示例 1：
输入：[2,1,4,7,3,2,5]
输出：5
解释：最长的 “山脉” 是 [1,4,7,3,2]，长度为 5。

示例 2：
输入：[2,2,2]
输出：0
解释：不含 “山脉”。

提示：
0 <= A.length <= 10000
0 <= A[i] <= 10000
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int longestMountain(vector<int>& A) {
        int n=A.size();
        vector<int> left(n, 0), right(n, 0); //记录i的左边和右边比i小的连续元素个数
        for(int i=1;i<n;i++){
            if(A[i-1]<A[i]) left[i]+=left[i-1]+1;
        }
        for(int i=n-2;i>=0;i--){
            if(A[i]>A[i+1]) right[i]+=right[i+1]+1;
        }
        int mx=0;
        for(int i=0;i<n;i++){
            if(left[i]>0&&right[i]>0)mx=max(mx, 1+left[i]+right[i]);
        }
        return mx;
    }
};

935. 骑士拨号器

Description
国际象棋中的骑士可以按下图所示进行移动：
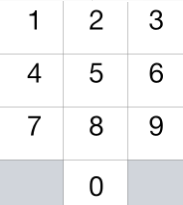
image)image
这一次，我们将 “骑士” 放在电话拨号盘的任意数字键（如上图所示）上，接下来，骑士将会跳 N-1 步。每一步必须是从一个数字键跳到另一个数字键。
每当它落在一个键上（包括骑士的初始位置），都会拨出键所对应的数字，总共按下 N 位数字。
你能用这种方式拨出多少个不同的号码？
因为答案可能很大，所以输出答案模 10^9 + 7。
Example
示例 1：
输入：1
输出：10

示例 2：
输入：2
输出：20

示例 3：
输入：3
输出：46

提示：
1 <= N <= 5000
Program
设DP[n][j]为第n步拨键j的总数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    vector<vector<int>> steps={
        {4,6},
        {6,8},
        {7,9},
        {4,8},
        {0,3,9},
        {},
        {0,1,7},
        {2,6},
        {1,3},
        {2,4}
    };
    const int MOD=1e9+7;
    int knightDialer(int N) {
        int DP[N+1][10];
        memset(DP, 0, sizeof(DP));
        for(int i=1;i<=N;i++){
            for(int j=0;j<=9;j++){
                if(i==1){
                    DP[i][j]=1;
                    continue;
                }
                for(int k=0;k<steps[j].size();k++){
                    DP[i][j]+=DP[i-1][steps[j][k]];
                    DP[i][j]%=MOD;
                }
            }
        }
        int ans=0;
        for(int i=0;i<=9;i++) ans=(ans+DP[N][i])%MOD;
        return ans;
    }
};

空间优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    vector<vector<int>> steps={
        {4,6},
        {6,8},
        {7,9},
        {4,8},
        {0,3,9},
        {},
        {0,1,7},
        {2,6},
        {1,3},
        {2,4}
    };
    const int MOD=1e9+7;
    int knightDialer(int N) {
        int tmpDp[10];
        int dp[10];
        fill(dp, dp+10, 1);
        fill(tmpDp, tmpDp+10, 0);
        for(int i=2;i<=N;i++){
            for(int j=0;j<=9;j++){
                for(int k=0;k<steps[j].size();k++){
                    tmpDp[j]+=dp[steps[j][k]];
                    tmpDp[j]%=MOD;
                }
            }
            for(int k=0;k<=9;k++){dp[k]=tmpDp[k];tmpDp[k]=0;}//tmpDp记得每次初始化
        }
        int ans=0;
        for(int i=0;i<=9;i++) ans=(ans+dp[i])%MOD;
        return ans;
    }
};

978. 最长湍流子数组

Description
当 $A$ 的子数组 $A[i], A[i+1], …, A[j]$ 满足下列条件时，我们称其为湍流子数组：
若 $i <= k < j$，当 $k$ 为奇数时， $A[k] > A[k+1]$，且当 $k$ 为偶数时，$A[k] < A[k+1]$；
或 若 $i <= k < j$，当 $k$ 为偶数时，$A[k] > A[k+1]$ ，且当 $k$ 为奇数时， $A[k] < A[k+1]$。
也就是说，如果比较符号在子数组中的每个相邻元素对之间翻转，则该子数组是湍流子数组。
返回 A 的最大湍流子数组的长度。
Example
示例 1：
输入：[9,4,2,10,7,8,8,1,9]
输出：5
解释：(A[1] > A[2] < A[3] > A[4] < A[5])

示例 2：
输入：[4,8,12,16]
输出：2

示例 3：
输入：[100]
输出：1

提示：
1 <= A.length <= 40000
0 <= A[i] <= 10^9
Program
动态规划
按题意分两种情况，这里为了方便判断后一个位置是否为奇数或者偶数，所以要相应改变：
设DP1[i]为以i为结尾的满足第一种条件的序列，DP2[i]为以i为结尾的满足第二种条件的序列，则有：
(1)如果i为奇数且A[i-1]<A[i]，或者i为偶数A[i-1]>A[i]，则DP1[i]=DP1[i-1]+1,否则DP1[1]=1； //自身
(2)如果i为奇数且A[i-1]>A[i],或者i为偶数A[i-1]<A[i]，则DP2[i]=DP1[i-1]+1,否则DP2][i]=1;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int maxTurbulenceSize(vector<int>& A) {
        int n=A.size();
        vector<int> DP1(n, 1), DP2(n, 1); //第一种序列，第二种序列
        int ans=1;
        for(int i=1;i<n;i++){
            if((i%2==1&&A[i-1]<A[i])||(i%2==0&&A[i-1]>A[i])){
                DP1[i]=DP1[i-1]+1;
            }
            if((i%2==1&&A[i-1]>A[i])||(i%2==0&&A[i-1]<A[i])){
                DP2[i]=DP2[i-1]+1;
            }
            ans=max(ans, DP1[i]);
            ans=max(ans, DP2[i]);
        }
        return ans;
    }
};

空间优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int maxTurbulenceSize(vector<int>& A) {
        int n=A.size();
        int dp1=1, dp2=1; //第一种序列，第二种序列
        int ans=1;
        for(int i=1;i<n;i++){
            if((i%2==1&&A[i-1]<A[i])||(i%2==0&&A[i-1]>A[i])){
                dp1+=1;
            }else dp1=1;
            if((i%2==1&&A[i-1]>A[i])||(i%2==0&&A[i-1]<A[i])){
                dp2+=1;
            }else dp2=1;
            ans=max(ans, dp1);
            ans=max(ans, dp2);
        }
        return ans;
    }
};

1191. K 次串联后最大子数组之和

Description
给你一个整数数组 arr 和一个整数 k。
首先，我们要对该数组进行修改，即把原数组 arr 重复 k 次。
举个例子，如果 arr = [1, 2] 且 k = 3，那么修改后的数组就是 [1, 2, 1, 2, 1, 2]。
然后，请你返回修改后的数组中的最大的子数组之和。
注意，子数组长度可以是 0，在这种情况下它的总和也是 0。
由于 结果可能会很大，所以需要 模（mod） 10^9 + 7 后再返回。
Example
示例 1：
输入：arr = [1,2], k = 3
输出：9

示例 2：
输入：arr = [1,-2,1], k = 5
输出：2

示例 3：
输入：arr = [-1,-2], k = 7
输出：0

提示：
1 <= arr.length <= 10^5
1 <= k <= 10^5
-10^4 <= arr[i] <= 10^4
Program
三种情况如下图所示，前两种好理解，只需返回对应的结果就行。
关键是第三种情况：
根据最大连续子数组之和的DP[i]=max(DP[i-1]+A[i],A[i])，可以知道当一段序列和大于0时，一定可以相连！
那么此时的结果为k-2个数组总和+2个数组中的最大DP值（注意此时2个数组中的最大DP值一定是与k-2个数组相连组成的最大子数组，因为若单个数组总和大于0，那么一定连接了整个数组，其次如果单个数组的后缀和使得整体和大于0，那么最后的结果肯定是包含单个数组的后缀+k-2个全数组+单个数组的前缀！这里单个数组的前缀后缀由两个数组的DP值决定）
例如:
-1,-2,4,5 | … | -1,-2,4,5
4,5,-1,-2|…|4,5,-1,-2
简单来说，
①单个数组和s大于0，直观来说k个数组都放在结果数组里和更大，但是最大的还得看两个单独数组的DP值组成的前后缀！如上面两个例子，结果都是从第一个4到最后一个5结束，但是分别不包含前面的-1，-2和最后的-1，-2！
②单个数组和s小于0（等于0没必要，抵消了，例如-1,-2,1,2），那么根据最大连续子数组之和的DP过程来看肯定会中断，如图第二种情况！即结果肯定在最多两个数组的DP结果产生。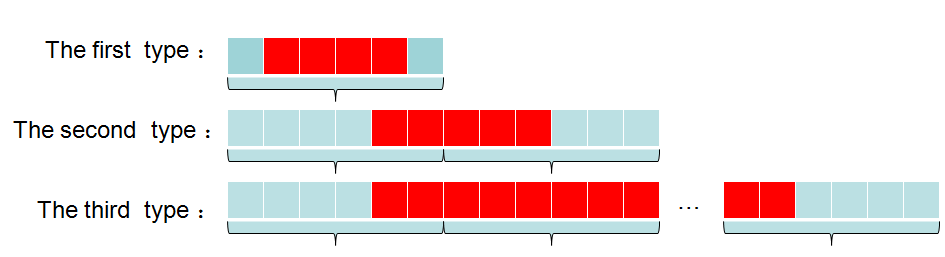
image
根据DP递推公式，只有前一项DP[i-1]+A[i]大于等于0时才能连续！
第一种情况成立的条件，

  • 考虑两个单独数组，第一个数组和第二个数组都有这一段最大子数组，那么第一个最大子数组的下一个位置的绝对值一定比该最大子数组的和大，且为负数！（中断了！）
  • 两个最大子数组之间当然也可能存在连续子数组但不是最大子数组！那么这之间所有可能的子数组（如果有）肯定不连续既然各个子数组不连续，那么相邻两个子数组之间肯定有个负数绝对值大于前一个子数组之和！
  • 而两个单独数组的最大子数组之间刚好又构成一个单独数组！根据分析，这个新的单独数组上的所有子数组（包括最大子数组），既然不连续，中断，一定有若干个负数绝对值大于这些子数组之和！
  • 即该单独数组的和小于0！

第二种情况成立条件：

  • 两个单独数组组成的最大子数组要想成立，这个最大子数组一定不会完全等于单独数组，也就是说由单独数组的后缀+前缀构成，而且不等价于单独数组，肯定元素比单独子数组个数少！。
  • 那么首先该最大子数组前面单独数组剩余部分的子数组（如果有），因为各个数组不连续，那么必然每个子数组后都有一个负数且绝对值比对应子数组之和大！
  • 其次，该最大子数组后面，也就是第二个单独数组，对应最大子数组起始元素前一个位置（从最大子数组头元素到此元素刚好构成一个单独数组），这一段，最大子数组后的一个元素是负数且绝对值比最大子数组和大！这个元素之后到最大子数组起始元素前，如果有若干子数组，则每个子数组后必存在一个负数绝对值比对应子数组之和大！因为各个子数组不连续，中断！
  • 即该单独数组之和小于0！（由上面分析，从最大子数组头元素到构成单独数组的最后一个元素这一段，每个子数组后都有个负数绝对值比该子数组和大！）

第三种情况成立条件：

  • 这里刚好解释下为什么第二种情况最大子数组不等价于单独子数组且元素个数更少，如果最大子数组末尾元素超过了后一个单独数组对应最大数组头元素，也就是说最大子数组覆盖了整个单独数组，那么表明单独数组之和大于等于0！
  • 如果单独数组之和大于等于0，那么必定后面一直连续到最后一个单独数组！也就是第三种情况了！
  • 很明显此时分为三部分，单独数组的后缀+k-2个全数组+单独数组前缀
    特殊情况：
    单独数组之和等于0！这个时候没必要连续到最后一个单独数组！因为中间这部分总和为0，最多只需求两个单独数组的最大子数组就可以了！
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    class Solution {
    public:
        typedef long long ll;
        const ll mod=1e9+7;
        int kConcatenationMaxSum(vector<int>& arr, int k) {
            ll s=0;
            for(int& x:arr) s+=x;
            ll dp=0;
            ll ans=0;
            for(int& x:arr){
                dp = dp + x>x?dp+x:x;
                ans = ans>dp?ans:dp;
            }
            if(k==1) return ans;
            for(int& x:arr){
                dp = dp + x>x?dp+x:x;
                ans = ans>dp?ans:dp;
            }
            if(k==2||s<=0) return ans;
            return (ans+((k-2)*s%mod+mod)%mod+mod)%mod;
        }
    };

    1218. 最长定差子序列

Description
给你一个整数数组 arr 和一个整数 difference，请你找出 arr 中所有相邻元素之间的差等于给定 difference 的等差子序列，并返回其中最长的等差子序列的长度。
Example
示例 1：
输入：arr = [1,2,3,4], difference = 1
输出：4
解释：最长的等差子序列是 [1,2,3,4]。

示例 2：
输入：arr = [1,3,5,7], difference = 1
输出：1
解释：最长的等差子序列是任意单个元素。

示例 3：
输入：arr = [1,5,7,8,5,3,4,2,1], difference = -2
输出：4
解释：最长的等差子序列是 [7,5,3,1]。

提示：
1 <= arr.length <= 10^5
-10^4 <= arr[i], difference <= 10^4
Program
动态规划：DP[i]=max(DP[i], DP[j]+1) if arr[i]-arr[j]==difference
但是时间复杂度$O(n^2)$，肯定超时。
那么这里记录arr[i]值最后出现的位置以及其dp值，因为同值arr[i]，后出现的dp值可能更高。
具体算法：
m记录值x最后出现时的dp值，m[x]=max(m[x], m[x-difference]+1)，注意x-difference有可能等于x，那么必须记录x值出现的位置，如果位置不同才能做max运算，否则m[x]=1；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int longestSubsequence(vector<int>& arr, int difference) {
        unordered_map<int,int> m; //记录值x最后出现时，dp值
        unordered_map<int,int> loc; //记录值x出现的位置
        int ans=0;
        for(int i=0;i<arr.size();i++){
            int x=arr[i];
            if(m.find(x)==m.end()) {m[x] = 1;loc[x]=i;}
            if(m.find(x-difference)!=m.end()&&loc[x-difference]!=i) m[x] = max(m[x], m[x-difference]+1);
            ans=max(m[x], ans);
        }
        return ans;
    }
};

1269. 停在原地的方案数

Description
有一个长度为 arrLen 的数组，开始有一个指针在索引 0 处。
每一步操作中，你可以将指针向左或向右移动 1 步，或者停在原地（指针不能被移动到数组范围外）。
给你两个整数 steps 和 arrLen ，请你计算并返回：在恰好执行 steps 次操作以后，指针仍然指向索引 0 处的方案数。
由于答案可能会很大，请返回方案数 模 10^9 + 7 后的结果。
Example
示例 1：
输入：steps = 3, arrLen = 2
输出：4
解释：3 步后，总共有 4 种不同的方法可以停在索引 0 处。
向右，向左，不动
不动，向右，向左
向右，不动，向左
不动，不动，不动

示例 2：
输入：steps = 2, arrLen = 4
输出：2
解释：2 步后，总共有 2 种不同的方法可以停在索引 0 处。
向右，向左
不动，不动

示例 3：
输入：steps = 4, arrLen = 2
输出：8

提示：
1 <= steps <= 500
1 <= arrLen <= 10^6
Progam
DP
设dp[i][s]为走了s步到数组i位置的方案数，状态转移方程：
dp[i][s] = dp[i + 1][s - 1] + dp[i - 1][s - 1] + dp[i][s - 1]
画一下二维坐标图，可以发现dp[i][s]只与前一列的结果相关，所以先循环s再遍历i进行dp
边界：dp[0][0] = 1；
时间复杂度：$O(s * min(s, arrLen))$，s为最大步骤数
空间复杂度: $O(s * min(s, arrLen))$, 滚动数组优化的话空间复杂度为$O(min(s, arrLen))$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    const int MOD = 1e9 + 7;
    int numWays(int steps, int arrLen) {
        int n = min(steps, arrLen); //找出最大可以到达的数组位置
        vector<vector<int>> dp(n, vector<int>(steps + 1, 0));
        dp[0][0] = 1; //边界
        for(int s = 1; s <= steps; s ++){
            for(int i = 0; i < n; i ++){
                dp[i][s] = dp[i][s - 1];
                if(i + 1 < n) dp[i][s] = (dp[i][s] + dp[i + 1][s - 1]) % MOD;
                if(i - 1 >= 0) dp[i][s] = (dp[i][s] + dp[i - 1][s - 1]) % MOD;
            }
        }
        return dp[0][steps];
    }
};

面试题 08.02. 迷路的机器人

Description
设想有个机器人坐在一个网格的左上角，网格 r 行 c 列。机器人只能向下或向右移动，但不能走到一些被禁止的网格（有障碍物）。设计一种算法，寻找机器人从左上角移动到右下角的路径。
image
网格中的障碍物和空位置分别用 1 和 0 来表示。
返回一条可行的路径，路径由经过的网格的行号和列号组成。左上角为 0 行 0 列。如果没有可行的路径，返回空数组。
Example
示例 1:
输入:

1
2
3
4
5
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]

输出: [[0,0],[0,1],[0,2],[1,2],[2,2]]
解释:
输入中标粗的位置即为输出表示的路径，即
0行0列（左上角） -> 0行1列 -> 0行2列 -> 1行2列 -> 2行2列（右下角）
说明：r 和 c 的值均不超过 100。
Program
思路
先用DP判断路径是否存在，若存在反向寻找路径。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<vector<int>> pathWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m=obstacleGrid.size();
        int n=obstacleGrid[0].size();
        if(obstacleGrid[0][0]==1||obstacleGrid[m-1][n-1]==1) return {}; //起点和终点时障碍物
        bool DP[m][n];
        memset(DP, false, sizeof(DP));
        DP[0][0]=true;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(obstacleGrid[i][j]==1) continue;
                if(i>0&&j>0) DP[i][j]=DP[i-1][j]||DP[i][j-1];
                else if(i>0) DP[i][j]=DP[i-1][j];
                else if(j>0) DP[i][j]=DP[i][j-1];
            }
        }
        if(!DP[m-1][n-1]) return {}; //无路径可达
        vector<vector<int>> res;
        int row=m-1, col=n-1;
        while(row>=0&&col>=0){
            res.push_back({row, col});
            if(row==0&&col==0) break; //退出循环
            if(row>0&&DP[row-1][col]) row--;
            else if(col>0&&DP[row][col-1])  col--;
        }
        reverse(res.begin(), res.end());
        return res;
    }
};

LCP 13. 寻宝

Description
我们得到了一副藏宝图，藏宝图显示，在一个迷宫中存在着未被世人发现的宝藏。

迷宫是一个二维矩阵，用一个字符串数组表示。它标识了唯一的入口（用 ‘S’ 表示），和唯一的宝藏地点（用 ‘T’ 表示）。但是，宝藏被一些隐蔽的机关保护了起来。在地图上有若干个机关点（用 ‘M’ 表示），只有所有机关均被触发，才可以拿到宝藏。

要保持机关的触发，需要把一个重石放在上面。迷宫中有若干个石堆（用 ‘O’ 表示），每个石堆都有无限个足够触发机关的重石。但是由于石头太重，我们一次只能搬一个石头到指定地点。

迷宫中同样有一些墙壁（用 ‘#’ 表示），我们不能走入墙壁。剩余的都是可随意通行的点（用 ‘.’ 表示）。石堆、机关、起点和终点（无论是否能拿到宝藏）也是可以通行的。

我们每步可以选择向上/向下/向左/向右移动一格，并且不能移出迷宫。搬起石头和放下石头不算步数。那么，从起点开始，我们最少需要多少步才能最后拿到宝藏呢？如果无法拿到宝藏，返回 -1 。
Example
示例 1：
输入： [“S#O”, “M..”, “M.T”]
输出：16
解释：最优路线为： S->O, cost = 4, 去搬石头 O->第二行的M, cost = 3, M机关触发 第二行的M->O, cost = 3, 我们需要继续回去 O 搬石头。 O->第三行的M, cost = 4, 此时所有机关均触发 第三行的M->T, cost = 2，去T点拿宝藏。 总步数为16。

示例 2：
输入： [“S#O”, “M.#”, “M.T”]
输出：-1
解释：我们无法搬到石头触发机关

示例 3：
输入： [“S#O”, “M.T”, “M..”]
输出：17
解释：注意终点也是可以通行的。
限制：
1 <= maze.length <= 100
1 <= maze[i].length <= 100
maze[i].length == maze[j].length
S 和 T 有且只有一个
0 <= M的数量 <= 16
0 <= O的数量 <= 40，题目保证当迷宫中存在 M 时，一定存在至少一个 O 。
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
class Solution {
public:
    int dx[4] = {1, -1, 0, 0};
    int dy[4] = {0, 0, 1, -1};
    int n, m;

    bool inBound(int x, int y) {
        return x >= 0 && x < n && y >= 0 && y < m;
    }

    vector<vector<int>> bfs(int x, int y, vector<string>& maze) {
        vector<vector<int>> ret(n, vector<int>(m, -1));
        ret[x][y] = 0;
        queue<pair<int, int>> Q;
        Q.push({x, y});
        while (!Q.empty()) {
            auto p = Q.front();
            Q.pop();
            int x = p.first, y = p.second;
            for (int k = 0; k < 4; k++) {
                int nx = x + dx[k], ny = y + dy[k];
                if (inBound(nx, ny) && maze[nx][ny] != '#' && ret[nx][ny] == -1) {
                    ret[nx][ny] = ret[x][y] + 1;
                    Q.push({nx, ny});
                }
            }
        }
        return ret;
    }

    int minimalSteps(vector<string>& maze) {
        n = maze.size(), m = maze[0].size();
        // 机关 & 石头
        vector<pair<int, int>> buttons, stones;
        // 起点 & 终点
        int sx, sy, tx, ty;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (maze[i][j] == 'M') {
                    buttons.push_back({i, j});
                }
                if (maze[i][j] == 'O') {
                    stones.push_back({i, j});
                }
                if (maze[i][j] == 'S') {
                    sx = i, sy = j;
                }
                if (maze[i][j] == 'T') {
                    tx = i, ty = j;
                }
            }
        }
        int nb = buttons.size();
        int ns = stones.size();
        vector<vector<int>> start_dist = bfs(sx, sy, maze);

        // 边界情况：没有机关
        if (nb == 0) {
            return start_dist[tx][ty];
        }
        // 从某个机关到其他机关 / 起点与终点的最短距离。
        vector<vector<int>> dist(nb, vector<int>(nb + 2, -1));
        // 中间结果
        vector<vector<vector<int>>> dd(nb);
        for (int i = 0; i < nb; i++) {
            vector<vector<int>> d = bfs(buttons[i].first, buttons[i].second, maze);
            dd[i] = d;
            // 从某个点到终点不需要拿石头
            dist[i][nb + 1] = d[tx][ty];
        }

        for (int i = 0; i < nb; i++) {
            int tmp = -1;
            for (int k = 0; k < ns; k++) {
                int mid_x = stones[k].first, mid_y = stones[k].second;
                if (dd[i][mid_x][mid_y] != -1 && start_dist[mid_x][mid_y] != -1) {
                    if (tmp == -1 || tmp > dd[i][mid_x][mid_y] + start_dist[mid_x][mid_y]) {
                        tmp = dd[i][mid_x][mid_y] + start_dist[mid_x][mid_y];
                    }
                }
            }
            dist[i][nb] = tmp;
            for (int j = i + 1; j < nb; j++) {
                int mn = -1;
                for (int k = 0; k < ns; k++) {
                    int mid_x = stones[k].first, mid_y = stones[k].second;
                    if (dd[i][mid_x][mid_y] != -1 && dd[j][mid_x][mid_y] != -1) {
                        if (mn == -1 || mn > dd[i][mid_x][mid_y] + dd[j][mid_x][mid_y]) {
                            mn = dd[i][mid_x][mid_y] + dd[j][mid_x][mid_y];
                        }
                    }
                }
                dist[i][j] = mn;
                dist[j][i] = mn;
            }
        }

        // 无法达成的情形
        for (int i = 0; i < nb; i++) {
            if (dist[i][nb] == -1 || dist[i][nb + 1] == -1) return -1;
        }

        // dp 数组， -1 代表没有遍历到
        vector<vector<int>> dp(1 << nb, vector<int>(nb, -1));
        for (int i = 0; i < nb; i++) {
            dp[1 << i][i] = dist[i][nb];
        }

        // 由于更新的状态都比未更新的大，所以直接从小到大遍历即可
        for (int mask = 1; mask < (1 << nb); mask++) {
            for (int i = 0; i < nb; i++) {
                // 当前 dp 是合法的
                if (mask & (1 << i)) {
                    for (int j = 0; j < nb; j++) {
                        // j 不在 mask 里
                        if (!(mask & (1 << j))) {
                            int next = mask | (1 << j);
                            if (dp[next][j] == -1 || dp[next][j] > dp[mask][i] + dist[i][j]) {
                                dp[next][j] = dp[mask][i] + dist[i][j];
                            }
                        }
                    }
                }
            }
        }

        int ret = -1;
        int final_mask = (1 << nb) - 1;
        for (int i = 0; i < nb; i++) {
            if (ret == -1 || ret > dp[final_mask][i] + dist[i][nb + 1]) {
                ret = dp[final_mask][i] + dist[i][nb + 1];
            }
        }

        return ret;
    }
};

前缀和系列

410. 分割数组的最大值

Description
给定一个非负整数数组和一个整数 m，你需要将这个数组分成 m 个非空的连续子数组。设计一个算法使得这 m 个子数组各自和的最大值最小。

注意:
数组长度 n 满足以下条件:
1 ≤ n ≤ 1000
1 ≤ m ≤ min(50, n)
Example
示例:
输入:
nums = [7,2,5,10,8]
m = 2
输出:
18

解释:
一共有四种方法将nums分割为2个子数组。
其中最好的方式是将其分为[7,2,5] 和 [10,8]，
因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。
Program
设DP[i][m]为将前i个元素划分成m份的目标值（最小和），则状态转移方程：
$DP[i][m]=min(max(DP[j][m-1], preSum[i]-perSum[j]))$，即前j个元素分成m-1份，后面(j,i]个元素成为一份！
时间复杂度：$O(m * n^2)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    const long inf=0x3f3f3f3f3f3f3f3f;
    int splitArray(vector<int>& nums, int m) {
        int n=nums.size();
        long DP[n+1][m+1];
        long preSum[n+1];
        memset(preSum, 0, sizeof(preSum));
        memset(DP, inf, sizeof(DP));
        for(int i=1;i<=n;i++){ //前缀和
            preSum[i]+=nums[i-1];
            preSum[i]+=preSum[i-1];
        }
        for(int i=1;i<=n;i++){
            for(int k=1;k<=min(i,m);k++){  //前i个元素最多分成i份
                if(k==1) {DP[i][1]=preSum[i];continue;}
                for(int j=k-1;j<i;j++){ //前i个元素分成k份，则前i-1个元素分成k-1分时，至少需要存在k-1个元素
                    //后面若干个为一份，前面j个元素分成k-1分
                    DP[i][k]=min(DP[i][k], max(DP[j][k-1], preSum[i]-preSum[j]));
                }
            }
        }
        return DP[n][m];
    }
};

1477. 找两个和为目标值且不重叠的子数组

Description
给你一个整数数组 arr 和一个整数值 target 。
请你在 arr 中找 两个互不重叠的子数组 且它们的和都等于 target 。可能会有多种方案，请你返回满足要求的两个子数组长度和的 最小值 。
请返回满足要求的最小长度和，如果无法找到这样的两个子数组，请返回 -1 。
Example
示例 1：
输入：arr = [3,2,2,4,3], target = 3
输出：2
解释：只有两个子数组和为 3 （[3] 和 [3]）。它们的长度和为 2 。

示例 2：
输入：arr = [7,3,4,7], target = 7
输出：2
解释：尽管我们有 3 个互不重叠的子数组和为 7 （[7], [3,4] 和 [7]），但我们会选择第一个和第三个子数组，因为它们的长度和 2 是最小值。

示例 3：
输入：arr = [4,3,2,6,2,3,4], target = 6
输出：-1
解释：我们只有一个和为 6 的子数组。

示例 4：
输入：arr = [5,5,4,4,5], target = 3
输出：-1
解释：我们无法找到和为 3 的子数组。

示例 5：
输入：arr = [3,1,1,1,5,1,2,1], target = 3
输出：3
解释：注意子数组 [1,2] 和 [2,1] 不能成为一个方案因为它们重叠了。

提示：
1 <= arr.length <= 10^5
1 <= arr[i] <= 1000
1 <= target <= 10^8
Program
DP
设DP[i]为前i个元素中存在子数组和为target的最小长度，我们希望状态转移方程：
（1）当[j+1, i]和为target时，$DP[i]=min(DP[i-1], i-j)$，其中[j+1,i]为和为target的子数组。关键在于找j，这里使用HashMap记录前缀和对应的下标！preSum[i]-target如果存在于HashMap，则进行DP；
（2）否则， DP[i]=DP[i-1]，表示与前i-1个元素的满足条件的子数组最小长度。
注意边界，以及题目要求的两满足条件的子数组的最小长度和！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    const int inf=0x3f3f3f3f;
    int minSumOfLengths(vector<int>& arr, int target) {
        int n=arr.size();
        unordered_map<int,int> sToi; //以i为结尾的前缀和对应的下标i
        sToi[0]=-1;
        int res=inf;
        int DP[n];
        memset(DP, inf, sizeof(DP));
        int sum=0;
        for(int i=0;i<n;i++){
            sum+=arr[i];
            sToi[sum]=i;
            if(sToi.count(sum-target)){
                int j=sToi[sum-target];
                DP[i]=min(i>0?DP[i-1]:inf, i-j);
                if(j>0) res=min(res, DP[j]+i-j); //j>0表示res必须计算两个子数组的长度和
            }else DP[i]=i>0?DP[i-1]:inf;//不能构成连续和为Target子数组
        }
        if(res==inf) return -1;//无解
        return res;
    }
};

1664. 生成平衡数组的方案数

Description
给你一个整数数组 nums 。你需要选择 恰好 一个下标（下标从 0 开始）并删除对应的元素。请注意剩下元素的下标可能会因为删除操作而发生改变。
比方说，如果 nums = [6,1,7,4,1] ，那么：
选择删除下标 1 ，剩下的数组为 nums = [6,7,4,1] 。
选择删除下标 2 ，剩下的数组为 nums = [6,1,4,1] 。
选择删除下标 4 ，剩下的数组为 nums = [6,1,7,4] 。
如果一个数组满足奇数下标元素的和与偶数下标元素的和相等，该数组就是一个 平衡数组 。
请你返回删除操作后，剩下的数组 nums 是 平衡数组 的 方案数 。
Example
示例 1：
输入：nums = [2,1,6,4]
输出：1
解释：
删除下标 0 ：[1,6,4] -> 偶数元素下标为：1 + 4 = 5 。奇数元素下标为：6 。不平衡。
删除下标 1 ：[2,6,4] -> 偶数元素下标为：2 + 4 = 6 。奇数元素下标为：6 。平衡。
删除下标 2 ：[2,1,4] -> 偶数元素下标为：2 + 4 = 6 。奇数元素下标为：1 。不平衡。
删除下标 3 ：[2,1,6] -> 偶数元素下标为：2 + 6 = 8 。奇数元素下标为：1 。不平衡。
只有一种让剩余数组成为平衡数组的方案。

示例 2：
输入：nums = [1,1,1]
输出：3
解释：你可以删除任意元素，剩余数组都是平衡数组。

示例 3：
输入：nums = [1,2,3]
输出：0
解释：不管删除哪个元素，剩下数组都不是平衡数组。

提示：
1 <= nums.length <= 105
1 <= nums[i] <= 104
Program
思路
（1）第i个位置删除后，后面[i+1, n]的奇变偶，偶变奇；
（2）所以直接一次遍历，判断两侧奇偶和是否相等；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int waysToMakeFair(vector<int>& nums) {
        int n=nums.size();
        vector<int> odd(n+1, 0);
        vector<int> even(n+1, 0);
        for(int i=1;i<=n;i++){
            if(i%2==0){
                odd[i]=odd[i-1]+nums[i-1];
                even[i]=even[i-1];
            }else{
                even[i]=even[i-1]+nums[i-1];
                odd[i]=odd[i-1];
            }
        }
        int ans=0;
        for(int i=1;i<=n;i++){
            int o=odd[i-1]+even[n]-even[i];
            int e=even[i-1]+odd[n]-odd[i];
            if(o==e) ans++;
        }
        return ans;
    }
};

巧妙
去除索引为ii的元素后，ii之前元素的奇偶性不变，ii之后元素的奇偶性改变，即ii之后奇/偶数下标元素的和变成了偶/奇数下标。
考虑奇偶元素的差值，我们求正负交替的前缀和 $dp[i] = \sum_{j=0}^{i} (-1)^j nums[j-1]$
那么dp[i-1]dp[i−1]表示索引ii左边部分奇偶元素差值，$dp[n] - dp[i]$表示索引ii右边部分奇偶元素差值，去除索引i后，$dp[n]−dp[i]$表示索引i右边部分奇偶元素差值的相反数。
因此，对任意i，只要$dp[i-1] == dp[n] - dp[i]$，即满足题目要求。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int waysToMakeFair(vector<int>& nums) {
        int n=nums.size();
        vector<int> dp(n+1, 0);
        for(int i=1;i<=n;i++){
            dp[i]=dp[i-1]+nums[i-1]*(i%2==0?1:-1);
        }
        int ans=0;
        for(int i=1;i<=n;i++){
            if(dp[i-1]==dp[n]-dp[i]) ans++;
        }
        return ans;
    }
};

5471. 和为目标值的最大数目不重叠非空子数组数目

Description
给你一个数组 nums 和一个整数 target 。
请你返回 非空不重叠 子数组的最大数目，且每个子数组中数字和都为 target 。
Example
示例 1：
输入：nums = [1,1,1,1,1], target = 2
输出：2
解释：总共有 2 个不重叠子数组（加粗数字表示） [1,1,1,1,1] ，它们的和为目标值 2 。

示例 2：
输入：nums = [-1,3,5,1,4,2,-9], target = 6
输出：2
解释：总共有 3 个子数组和为 6 。
([5,1], [4,2], [3,5,1,4,2,-9]) 但只有前 2 个是不重叠的。

示例 3：
输入：nums = [-2,6,6,3,5,4,1,2,8], target = 10
输出：3

示例 4：
输入：nums = [0,0,0], target = 0
输出：3

提示：
1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
0 <= target <= 10^6
Program
动态规划
设DP[i]是前i个中满足题意的最大个数，那么状态转移方程为：
如果[j+1,i]和为target，那么DP[i]=max(DP[i-1], DP[j]+1);
否则DP[i]=DP[i-1]；
时间复杂度：$O(n^2)$，显然对于这样的复杂度是不可接受的，超时！
这里利用Hash表存储以i为结尾的前缀和的下标i，通过hash表找出preSum[i]-target的j是否存在，如果存在进行DP，否则DP[i]=DP[i-1]；
注意边界，Hash[0]=-1，因为可能存在[0..i]为target的情况！
时间复杂度：$O(n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int maxNonOverlapping(vector<int>& nums, int target) {
        int n=nums.size();
        int DP[n];
        memset(DP, 0, sizeof(DP));
        unordered_map<int,int> sToi;//前缀和的尾元素坐标
        int sum=0;
        sToi[0]=-1;
        for(int i=0;i<n;i++){
            sum+=nums[i];
            if(sToi.find(sum-target)!=sToi.end()){
                int j=sToi[sum-target];
                DP[i]=max((i>0?DP[i-1]:0), ((j>=0?DP[j]:0)+1));
            }else DP[i]=(i>0?DP[i-1]:0);
            sToi[sum]=i;
        }
        return DP[n-1];
    }
};

区间DP

5. 最长回文子串

Description
给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
Example
示例 1：
输入: “babad”
输出: “bab”
注意: “aba” 也是一个有效答案。

示例 2：
输入: “cbbd”
输出: “bb”
Program
动态规划
设DP[i][j]为[i,j]是否为回文串，是为1，否为0；
状态转移方程：DP[i][j]=DP[i+1][j-1]&(s[i]==s[j])
时间复杂度：$O(n^2)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    string longestPalindrome(string s) {
        int n=s.length();
        if(n==0) return s;
        vector<vector<int>> DP;
        DP.resize(n);
        int maxLen=1, l=0, r=0;
        for(int i=0;i<n;i++){
            DP[i].resize(n, 0);
            DP[i][i]=1;
        }
        for(int i=0;i<n-1;i++){
            if(s[i]==s[i+1]){
                DP[i][i+1]=1;
                if(maxLen==1){
                    maxLen=2;
                    l=i;
                    r=i+1;
                }
            }
        }
        for(int len=3;len<=n;len++){
            for(int i=0;i+len-1<n;i++){
                int j=i+len-1;
                if(s[i]==s[j]) DP[i][j]=DP[i+1][j-1];
                if(DP[i][j]==1&&len>maxLen){
                    maxLen=len;
                    l=i;
                    r=j;
                }
            }
        }
        return s.substr(l, maxLen);
    }
};

中心扩展法
image
由于存在奇数的回文串和偶数的回文串，所以需要从一个字符开始扩展或者从两个字符之间进行扩展。
时间复杂度：$O(n^2)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    string longestPalindrome(string s) {
        int n=s.length();
        int start, end;
        start=end=0;
        for(int i=0;i<n;i++){
            pair<int,int> p1=expandAroundCenter(s, i, i);
            pair<int,int> p2=expandAroundCenter(s, i, i+1);
            pair<int,int> p;
            if(p1.second-p1.first>=p2.second-p2.first) p=p1;
            else p=p2;
            if(p.second-p.first>end-start){
                start=p.first;
                end=p.second;
            }
        }
        return s.substr(start, end-start+1);
    }
    pair<int,int> expandAroundCenter(string& s, int left, int right){
        int n=s.length();
        while(left>=0&&right<n&&s[left]==s[right]){
            left--;
            right++;
        }
        return {++left, --right};
    }
};

马拉车算法
（1）首先对原始字符串用其不包含的字符进行扩充，例如用’#’，得到的字符串长度一定为奇数
（2）其次设P[i]为处理后的串的每个字符对应的以i为中心的回文串长度，其在原始字符串的起始坐标为(i-P[i])/2
（3）利用对称性，更新P[i]、R、C。详见参考：
参考链接
时间复杂度：$O(n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Solution {
public:
    string longestPalindrome(string s) {
        int n=s.length();
        if(n<2) return s;
        string str=addBoundaries(s, '#');
        n=str.length();
        int P[n];
        memset(P, 0, sizeof(P));
        int R=0,C=0; //右边界与中心点,R=C+P[C],P[i]表示以i为中心点的原始回文串长度，也可以表示处理后的字符串的以i为中心的回文串半径，处理后的字符串长度一定为奇数
        int start=0, end=0; //最长回文串的起始位置

        for(int i=0;i<n;i++){
            if(i<R){
                int i_mirror = 2 * C - i;//i关于center对承德店i_mirror
                //P[i_mirror]的三种情况
                //①P[i_mirror]<R-i,P[i]=P[i_mirror],无需扩展
                //②P[i_mirror]=R-i,P[i]=P[i_mirror]，需要扩展
                //③P[i_mirror]>R-i，P[i]=R-i，无需扩展
                //min精髓，当然后面还要考虑是否中心扩展
                P[i]=min(R-i, P[i_mirror]);
            }

            int left=i-P[i]-1;
            int right=i+P[i]+1;
            while(left>=0&&right<n&&str[left]==str[right]){
                P[i]++;
                left--;
                right++;
            }
            if(i+P[i]>R){ //更新R,C
                R=i+P[i];
                C=i;
            }
            if(P[i]>end-start+1){
                start=(i-P[i])/2; //起始点关系
                end=start+P[i]-1;
            }
        }
        return s.substr(start, end-start+1);
    }


    string addBoundaries(string s, char divide){ //分隔符divide必须是字符串中未出现的字符
        int n=s.length();
        if(n==0) return "";
        string res;
        for(int i=0;i<n;i++){
            res+=divide;
            res+=s[i];
        }
        res+=divide;
        return res;
    }
};

303. 区域和检索 - 数组不可变

Description
给定一个整数数组 nums，求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和，包含 i, j 两点。
Example
示例：
给定 nums = [-2, 0, 3, -5, 2, -1]，求和函数为 sumRange()

1
2
3
sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3

说明:
你可以假设数组不可变。
会多次调用 sumRange 方法。
Progam

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class NumArray {
public:
    vector<int> DP;
    NumArray(vector<int>& nums) {
        int sum=0;
        for(int x:nums){
            sum+=x;
            DP.push_back(sum);
        }
    }

    int sumRange(int i, int j) {
        if(i==0) return DP[j];
        return DP[j]-DP[i-1];
    }
};

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray* obj = new NumArray(nums);
 * int param_1 = obj->sumRange(i,j);
 */

304. 二维区域和检索 - 矩阵不可变

Description
给定一个二维矩阵，计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2)。
image
上图子矩阵左上角 (row1, col1) = (2, 1) ，右下角(row2, col2) = (4, 3)，该子矩形内元素的总和为 8。
Example
示例:

1
2
3
4
5
6
7
8
9
10
给定 matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]
sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

说明:

你可以假设矩阵不可变。
会多次调用 sumRegion 方法。
你可以假设 row1 ≤ row2 且 col1 ≤ col2。
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class NumMatrix {
public:
    vector<vector<int>> DP;
    NumMatrix(vector<vector<int>>& matrix) {
        if(matrix.size()==0) return;
        int m=matrix.size();
        int n=matrix[0].size();
        DP.resize(m);
        for(int i=0;i<m;i++) DP[i].resize(n, 0);
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                DP[i][j]+=matrix[i][j];
                if(i-1>=0) DP[i][j]+=DP[i-1][j];
                if(j-1>=0) DP[i][j]+=DP[i][j-1];
                if(i-1>=0&&j-1>=0) DP[i][j]-=DP[i-1][j-1];
            }
        }
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        if(DP.size()==0) return 0;
        int result=DP[row2][col2];
        if(row1==0&&col1==0) return result;
        if(row1-1>=0) result-=DP[row1-1][col2];
        if(col1-1>=0) result-=DP[row2][col1-1];
        if(row1-1>=0&&col1-1>=0) result+=DP[row1-1][col1-1];
        return result;
    }
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix* obj = new NumMatrix(matrix);
 * int param_1 = obj->sumRegion(row1,col1,row2,col2);
 */

375. 猜数字大小 II

Description
我们正在玩一个猜数游戏，游戏规则如下：
我从 1 到 n 之间选择一个数字，你来猜我选了哪个数字。
每次你猜错了，我都会告诉你，我选的数字比你的大了或者小了。
然而，当你猜了数字 x 并且猜错了的时候，你需要支付金额为 x 的现金。直到你猜到我选的数字，你才算赢得了这个游戏。
Example
示例:
n = 10, 我选择了8.
第一轮: 你猜我选择的数字是5，我会告诉你，我的数字更大一些，然后你需要支付5块。
第二轮: 你猜是7，我告诉你，我的数字更大一些，你支付7块。
第三轮: 你猜是9，我告诉你，我的数字更小一些，你支付9块。
游戏结束。8 就是我选的数字。
你最终要支付 5 + 7 + 9 = 21 块钱。
给定 n ≥ 1，计算你至少需要拥有多少现金才能确保你能赢得这个游戏。
Program
①暴力
$DP[1, n]=min(i+max(DP[1, i-1], DP[i+1, n])), i\in[1, n]$;
选择第i个数，然后比较左右两边值大小去最大值，最后去所有i下最小值
时间复杂度: $O(n!)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int cal(int l, int r){
        if(l>=r) return 0;
        int minValue=0x3f3f3f3f;
        for(int i=l;i<=r;i++){
            int value=i+max(cal(l,i-1), cal(i+1, r));
            minValue=min(minValue, value);
        }
        return minValue;
    }
    int getMoneyAmount(int n) {
        return cal(1, n);
    }
};

②DP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int getMoneyAmount(int n) {
        vector<vector<int>> DP(n+1);
        for(int i=0;i<n+1;i++) DP[i].resize(n+1, 0);
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                int minValue=0x3f3f3f3f;
                for(int k=i;k<=j;k++){
                    int value=0;
                    if(k+1<=j) value=k+max(DP[i][k-1], DP[k+1][j]);
                    else value=k+DP[i][k-1];
                    minValue=min(minValue, value);
                }
                DP[i][j]=minValue;
            }
        }
        return DP[1][n];
    }

一般思路可能那么写代码，但是注意这种写法顺序$DP[k+1][j]$在没计算出来之前就被用到了！！！
所以就不能那么写！
注意每次抽取k值，那么会导致一段一段的$DP[i][j]$，有没有感觉？？最长回文子串的写法！！！
时间复杂度：$O(n^3)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int getMoneyAmount(int n) {
        vector<vector<int>> DP(n+1);
        for(int i=0;i<n+1;i++) DP[i].resize(n+1, 0);
        for(int len=2;len<=n;len++){
            for(int i=1;i<=n-len+1;i++){
                int j=i+len-1;
                int minValue=0x3f3f3f3f;
                for(int k=i;k<=j;k++){
                    int value=0;
                    if(k==j) value=k+DP[i][k-1];
                    else if(k==i) value=k+DP[k+1][j];
                    else value=k+max(DP[i][k-1], DP[k+1][j]);
                    minValue=min(minValue, value);
                }
                DP[i][j]=minValue;
            }
        }
        return DP[1][n];
    }

};

516. 最长回文子序列

Description
给定一个字符串s，找到其中最长的回文子序列。可以假设s的最大长度为1000。
Example
示例 1:
输入:
“bbbab”
输出:
4
一个可能的最长回文子序列为 “bbbb”。

示例 2:
输入:
“cbbd”
输出:
2
一个可能的最长回文子序列为 “bb”。
Program
最长回文子串以及最长公共子序列的翻版！注意子串以及子序列的区别！
设DP[i][j]表示i…j这部分的回文子序列，那么当s[i]=s[j]时，明显DP[i][j]=DP[i+1][j-1]+2,反之DP[i][j]=max(DP[i][j-1], DP[i+1][j]);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int longestPalindromeSubseq(string s) {
        if(s.length()==0) return 0;
        int n=s.length();
        vector<vector<int>> DP(n, vector<int>(n ,1));
        for(int i=0;i<n;i++){
            if(i+1<n&&s[i]==s[i+1]) DP[i][i+1]=2;
        }
        for(int len=3;len<=n;len++){
            for(int i=0;i+len-1<n;i++){
                int j=i+len-1;
                if(s[i]==s[j]) DP[i][j]=DP[i+1][j-1]+2;
                else DP[i][j]=max(DP[i+1][j], DP[i][j-1]);
            }
        }
        return DP[0][n-1];
    }
};

647. 回文子串

Description
给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。
具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被计为是不同的子串。
Example
示例 1:
输入: “abc”
输出: 3
解释: 三个回文子串: “a”, “b”, “c”.

示例 2:
输入: “aaa”
输出: 6
说明: 6个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”.
注意:
输入的字符串长度不会超过1000。
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int countSubstrings(string s) {
        int n=s.length();
        vector<vector<int>>DP(n, vector<int>(n, 0));
        for(int i=0;i<n;i++){
            DP[i][i]=1;
            if(i+1<n&&s[i]==s[i+1]) DP[i][i+1]=1;
        }
        for(int len=3;len<=n;len++){
            for(int i=0;i+len-1<n;i++){
                int j=i+len-1;
                if(s[i]==s[j]) DP[i][j]=DP[i+1][j-1];
            }
        }
        int ans=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++) ans+=DP[i][j];
        }
        return ans;
    }
};

764. 最大加号标志

Description
在一个大小在 (0, 0) 到 (N-1, N-1) 的2D网格 grid 中，除了在 mines 中给出的单元为 0，其他每个单元都是 1。网格中包含 1 的最大的轴对齐加号标志是多少阶？返回加号标志的阶数。如果未找到加号标志，则返回 0。

一个 k” 阶由 1 组成的“轴对称”加号标志具有中心网格 grid[x][y] = 1 ，以及4个从中心向上、向下、向左、向右延伸，长度为 k-1，由 1 组成的臂。下面给出 k” 阶“轴对称”加号标志的示例。注意，只有加号标志的所有网格要求为 1，别的网格可能为 0 也可能为 1。

k 阶轴对称加号标志示例:

阶 1:
000
010
000

阶 2:
00000
00100
01110
00100
00000

阶 3:
0000000
0001000
0001000
0111110
0001000
0001000
0000000
Example
示例 1：
输入: N = 5, mines = [[4, 2]]
输出: 2
解释:
11111
11111
11111
11111
11011
在上面的网格中，最大加号标志的阶只能是2。一个标志已在图中标出。

示例 2：
输入: N = 2, mines = []
输出: 1
解释:
11
11
没有 2 阶加号标志，有 1 阶加号标志。

示例 3：
输入: N = 1, mines = [[0, 0]]
输出: 0
解释:
0
没有加号标志，返回 0 。

提示：
整数N 的范围： [1, 500].
mines 的最大长度为 5000.
mines[i] 是长度为2的由2个 [0, N-1] 中的数组成.
(另外,使用 C, C++, 或者 C# 编程将以稍小的时间限制进行​​判断.)
Progarm
1，定义数组arm[N][N][4]为点在四方向上延伸的最大长度
arm[i][j][0]代表点[i, j]向上最长延伸的1的最大长度
arm[i][j][1]代表点[i, j]向左最长延伸的1的最大长度
arm[i][j][2]代表点[i, j]向下最长延伸的1的最大长度
arm[i][j][3]代表点[i, j]向右最长延伸的1的最大长度
2，遍历所有点四方向延伸手臂最小值的最大值即可
找到max{min{arm[i][j][0], arm[i][j][1], arm[i][j][2], arm[i][j][3]}}即是答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
public:
    int orderOfLargestPlusSign(int N, vector<vector<int>>& mines) {
        int m[N][N];
        int arms[N][N][4];
        memset(m, -1, sizeof(m));
        memset(arms, 0, sizeof(arms));
        for(vector<int> vec:mines){
            int x=vec[0];
            int y=vec[1];
            m[x][y]=0;
        }
        for(int i=0;i<N;i++){
            for(int j=0;j<N;j++){
                if(m[i][j]!=0){
                    arms[i][j][0]=(i>0?arms[i-1][j][0]:0)+1;
                    arms[i][j][1]=(j>0?arms[i][j-1][1]:0)+1;
                }   
            }
        }
        for(int i=N-1;i>=0;i--){
            for(int j=N-1;j>=0;j--){
                if(m[i][j]!=0){
                    arms[i][j][2]=(i<N-1?arms[i+1][j][2]:0)+1;
                    arms[i][j][3]=(j<N-1?arms[i][j+1][3]:0)+1;
                }
            }
        }
        int ans=0;
        for(int i=0;i<N;i++){
            for(int j=0;j<N;j++){
                int min1=min(arms[i][j][0],arms[i][j][1]);
                int min2=min(arms[i][j][2],arms[i][j][3]);
                min1=min(min1,min2);
                ans=max(ans,min1);
            }
        }
        return ans;
    }
};

1024. 视频拼接

Description
你将会获得一系列视频片段，这些片段来自于一项持续时长为 T 秒的体育赛事。这些片段可能有所重叠，也可能长度不一。
视频片段 clips[i] 都用区间进行表示：开始于 clips[i][0] 并于 clips[i][1] 结束。我们甚至可以对这些片段自由地再剪辑，例如片段 [0, 7] 可以剪切成 [0, 1] + [1, 3] + [3, 7] 三部分。
我们需要将这些片段进行再剪辑，并将剪辑后的内容拼接成覆盖整个运动过程的片段（[0, T]）。返回所需片段的最小数目，如果无法完成该任务，则返回 -1 。
Example
示例 1：
输入：clips = [[0,2],[4,6],[8,10],[1,9],[1,5],[5,9]], T = 10
输出：3
解释：
我们选中 [0,2], [8,10], [1,9] 这三个片段。
然后，按下面的方案重制比赛片段：
将 [1,9] 再剪辑为 [1,2] + [2,8] + [8,9] 。
现在我们手上有 [0,2] + [2,8] + [8,10]，而这些涵盖了整场比赛 [0, 10]。

示例 2：
输入：clips = [[0,1],[1,2]], T = 5
输出：-1
解释：
我们无法只用 [0,1] 和 [0,2] 覆盖 [0,5] 的整个过程。

示例 3：
输入：clips = [[0,1],[6,8],[0,2],[5,6],[0,4],[0,3],[6,7],[1,3],[4,7],[1,4],[2,5],[2,6],[3,4],[4,5],[5,7],[6,9]], T = 9
输出：3
解释：
我们选取片段 [0,4], [4,7] 和 [6,9] 。

示例 4：
输入：clips = [[0,4],[2,8]], T = 5
输出：2
解释：
注意，你可能录制超过比赛结束时间的视频。

提示：
1 <= clips.length <= 100
0 <= clips[i][0] <= clips[i][1] <= 100
0 <= T <= 100
Program
动态规划
设DP[i]是以i为结束的最小数目：
（1）以HashMap记录以i为结尾的所有区间的起始点，这里需要将区间[s,e]中每个以s开头，j(j=s,…e)为结尾的区间都算进去；
（2）递推方程：DP[i]=min(DP[i],1+DP[m[i][j])，其中j为以i结尾的区间的索引，0表示该区间起始。
边界：

  • 如果m[0].size()==0，表示没有以0开头的区间，如果m[T].size()==0，表示没有以T为结尾的区间，所以直接返回false；
  • 否则DP[0]=0
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    class Solution {
    public:
        const int inf=0x3f3f3f3f;
        int videoStitching(vector<vector<int>>& clips, int T) {
            unordered_map<int, vector<int> > m;//记录以i为结尾的区间
            for(vector<int>& vec:clips){
                int s=vec[0];
                int e=vec[1];
                for(int i=s;i<=e;i++){ //拆分区间
                    m[i].push_back(s);
                }
            }
            int DP[T+1];
            memset(DP, inf, sizeof(DP));
            if(m[T].size()==0||m[0].size()==0) return -1;
            DP[0]=0;
            for(int i=0;i<=T;i++){
                for(int j=0;j<m[i].size();j++){
                    int s=m[i][j];
                    DP[i]=min(DP[i], 1+DP[s]);
                }
                //cout<<DP[i]<<endl;
            }
            return DP[T]==inf?-1:DP[T]; //未找到连通区间
        }
    };

贪心
DP[i]记录以i为起点的最远可达距离。
思路还是挺简洁的，先按照其实时间位置正序排序。对于每一个clip,当超过前一次跳跃所能达到的最大位置时，跳跃次数加一并更新临界位置的坐标。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int videoStitching(vector<vector<int>>& clips, int T) {
        int dp[101] ={0};
        int mx = 0, ans = 0, pre = 0;
        for (vector<int>& clip : clips) {
            dp[clip[0]] = max(dp[clip[0]], clip[1]);
        }
        for (int i = 0; i < T; i++) {
            mx = max(mx, dp[i]);
            if (i == pre) { //已到达上一区间所能到达的最远距离
                ans++;  
                pre = mx;
            }
            if (i == mx) return -1; //不可达
        }
        return ans;
    }
};

1039. 多边形三角剖分的最低得分

Description
给定 N，想象一个凸 N 边多边形，其顶点按顺时针顺序依次标记为 A[0], A[i], …, A[N-1]。
假设您将多边形剖分为 N-2 个三角形。对于每个三角形，该三角形的值是顶点标记的乘积，三角剖分的分数是进行三角剖分后所有 N-2 个三角形的值之和。
返回多边形进行三角剖分后可以得到的最低分。
Example
示例 1：
输入：[1,2,3]
输出：6
解释：多边形已经三角化，唯一三角形的分数为 6。

示例 2：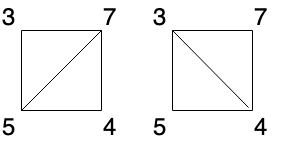
image
输入：[3,7,4,5]
输出：144
解释：有两种三角剖分，可能得分分别为：$375 + 457 = 245，或 345 + 347 = 144$。最低分数为 144。

示例 3：
输入：[1,3,1,4,1,5]
输出：13
解释：最低分数三角剖分的得分情况为 $113 + 114 + 115 + 111 = 13$。

提示：
3 <= A.length <= 50
1 <= A[i] <= 100
Program
动态规划
设DP[i][j]为以[i,j]为多边形的最低得分，则$DP[i][j]=min(DP[i][m]+A[i]A[m]A[j]+DP[m][j]), m=i+1,…,j-1$
即DP[i][j]划分成N-2个三角形，恰好以i,j为三角形两端点，m为另一端点，然后将多边形划分成DP[i][m],以及i,j,m组成的三角形，以及DP[m][j]三个部分，
可以发现DP[i][m]为m-i+1-2个划分，DP[m][j]为j-m+1-2个划分，
所以总的划分刚好为$m-i+1-2+j-m+1-2+1=j-i+1-2$满足题意。
注意DP[i][j]与后面某行DP[m][j]以及左侧DP[i][m]有关，所以应当从下往上，从左往右DP。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    const int inf=0x3f3f3f3f;
    int minScoreTriangulation(vector<int>& A) {
        int n=A.size();
        int DP[n][n];
        memset(DP, 0, sizeof(DP));
        for(int i=n-3;i>=0;i--){
            for(int j=i+2;j<n;j++){
                for(int m=i+1;m<j;m++){
                    if(DP[i][j]==0) DP[i][j]=DP[i][m]+A[i] * A[j] * A[m]+DP[m][j]; //初始化
                    else DP[i][j]=min(DP[i][j], DP[i][m]+A[i] * A[j] * A[m]+DP[m][j]);
                }
            }
        }
        return DP[0][n-1];
    }
};

1105. 填充书架

Description
给你一个 m * n 的矩阵 mat 和一个整数 K ，请你返回一个矩阵 answer ，其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和：

  • i - K <= r <= i + K, j - K <= c <= j + K
  • (r, c) 在矩阵内。

Example
示例 1：
输入：mat = [[1,2,3],[4,5,6],[7,8,9]], K = 1
输出：[[12,21,16],[27,45,33],[24,39,28]]

示例 2：
输入：mat = [[1,2,3],[4,5,6],[7,8,9]], K = 2
输出：[[45,45,45],[45,45,45],[45,45,45]]

提示：
m == mat.length
n == mat[i].length
1 <= m, n, K <= 100
1 <= mat[i][j] <= 100
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int m, n;
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int K) {
        m=mat.size(), n=mat[0].size();
        int DP[m+1][n+1]; //多开一维，免得边界判断
        memset(DP, 0, sizeof(DP));
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                DP[i][j]=DP[i][j-1]+DP[i-1][j]-DP[i-1][j-1]+mat[i-1][j-1];
            }
        }
        vector<vector<int>> A(m+1, vector<int>(n+1, 0)); //多开一维，方便边界运算，比如i-K,j-K不在矩阵范围内，可以使用A[0][X]以及A[X][0]
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                int down=(i-K-1<1)?0:i-K-1;
                int up=(i+K>m)?m:i+K;
                int left=(j-K-1<1)?0:j-K-1;
                int right=(j+K>n)?n:j+K;
                A[i][j]=DP[up][right]-DP[up][left]-DP[down][right]+DP[down][left];
                mat[i-1][j-1]=A[i][j];
            }
        }
        return mat;
    }
};

Description
附近的家居城促销，你买回了一直心仪的可调节书架，打算把自己的书都整理到新的书架上。
你把要摆放的书 books 都整理好，叠成一摞：从上往下，第 i 本书的厚度为 books[i][0]，高度为 books[i][1]。
按顺序 将这些书摆放到总宽度为 shelf_width 的书架上。
先选几本书放在书架上（它们的厚度之和小于等于书架的宽度 shelf_width），然后再建一层书架。重复这个过程，直到把所有的书都放在书架上。
需要注意的是，在上述过程的每个步骤中，摆放书的顺序与你整理好的顺序相同。 例如，如果这里有 5 本书，那么可能的一种摆放情况是：第一和第二本书放在第一层书架上，第三本书放在第二层书架上，第四和第五本书放在最后一层书架上。
每一层所摆放的书的最大高度就是这一层书架的层高，书架整体的高度为各层高之和。
以这种方式布置书架，返回书架整体可能的最小高度。
Example
示例：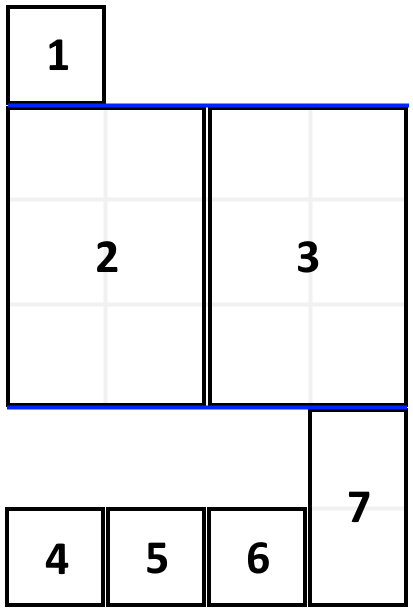
image
输入：books = [[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]], shelf_width = 4
输出：6
解释：
3 层书架的高度和为 1 + 3 + 2 = 6 。
第 2 本书不必放在第一层书架上。

提示：
1 <= books.length <= 1000
1 <= books[i][0] <= shelf_width <= 1000
1 <= books[i][1] <= 1000
Program
深搜
超时。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int minH;
    int n;
    int shelfWidth;
    void dfs(vector<vector<int>>& books, int i, int sumH){
        if(i==n){
            minH=min(minH, sumH);
            return;
        }
        int nowWidth=0;
        int maxH=0;
        for(int j=i;j<n&&nowWidth+books[j][0]<=shelfWidth;j++){
            nowWidth+=books[j][0];
            maxH=max(maxH, books[j][1]);
            dfs(books, j+1, sumH+maxH);
        }
    }
    int minHeightShelves(vector<vector<int>>& books, int shelf_width) {
        minH=INT_MAX;
        shelfWidth=shelf_width;
        n=books.size();
        dfs(books, 0, 0);
        return minH;
    }
};

动规
设DP[i]为i本书取得的最小高度，前i-1本书分别已求得最小高度值，求i本书最小高度：
可以知道第i本书一定在最后一层，那么其最多有满足witdh<=shelf_w的书在同一层，即最后一层，求其中最小高度即可：
DP[i]=min(DP[i], DP[j-1]+h)，其中j为最后一层书籍的头一本书索引，h为最后一层书的最大高度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    const int inf=0x3f3f3f3f;
    int minHeightShelves(vector<vector<int>>& books, int shelf_width) {
        int n=books.size();
        vector<int> DP(n, inf);
        for(int i=0;i<n;i++){
            int width=0;
            int h=0;
            for(int j=i;j>=0;j--){
                width+=books[j][0];
                if(width>shelf_width) break;
                h=max(h, books[j][1]);
                DP[i]=min(DP[i], ((j>=1)?DP[j-1]+h:h));
            }
        }
        return DP[n-1];
    }
};

1139. 最大的以 1 为边界的正方形

Description
给你一个由若干 0 和 1 组成的二维网格 grid，请你找出边界全部由 1 组成的最大 正方形 子网格，并返回该子网格中的元素数量。如果不存在，则返回 0。
Example
示例 1：
输入：grid = [[1,1,1],[1,0,1],[1,1,1]]
输出：9

示例 2：
输入：grid = [[1,1,0,0]]
输出：1

提示：
1 <= grid.length <= 100
1 <= grid[0].length <= 100
grid[i][j] 为 0 或 1
Program
与最大正方形类似，这里需要记录grid[i][j]==1时 包含自身 的左边与上边连续1的个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int largest1BorderedSquare(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<vector<int>> leftOnes(m ,vector<int>(n ,0));
        vector<vector<int>> upOnes(m, vector<int>(n, 0));
        int ans=0;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(grid[i][j]==0) continue;
                leftOnes[i][j]=1;
                upOnes[i][j]=1;
                if(i>0) upOnes[i][j]+=upOnes[i-1][j];
                if(j>0) leftOnes[i][j]+=leftOnes[i][j-1];
                for(int k=1;k<=min(upOnes[i][j], leftOnes[i][j]);k++){
                    if(k>ans&&upOnes[i][j-k+1]>=k&&leftOnes[i-k+1][j]>=k){
                        ans=k;
                    }
                }
            }
        }
        return ans*ans;
    }
};

1240. 铺瓷砖

Description
你是一位施工队的工长，根据设计师的要求准备为一套设计风格独特的房子进行室内装修。
房子的客厅大小为 n x m，为保持极简的风格，需要使用尽可能少的 正方形 瓷砖来铺盖地面。
假设正方形瓷砖的规格不限，边长都是整数。
请你帮设计师计算一下，最少需要用到多少块方形瓷砖？
Example
示例 1：
image
输入：n = 2, m = 3
输出：3
解释：3 块地砖就可以铺满卧室。
2 块 1x1 地砖
1 块 2x2 地砖

示例 2：
image
输入：n = 5, m = 8
输出：5

示例 3：
image
输入：n = 11, m = 13
输出：6

提示：
1 <= n <= 13
1 <= m <= 13
Program
动态规划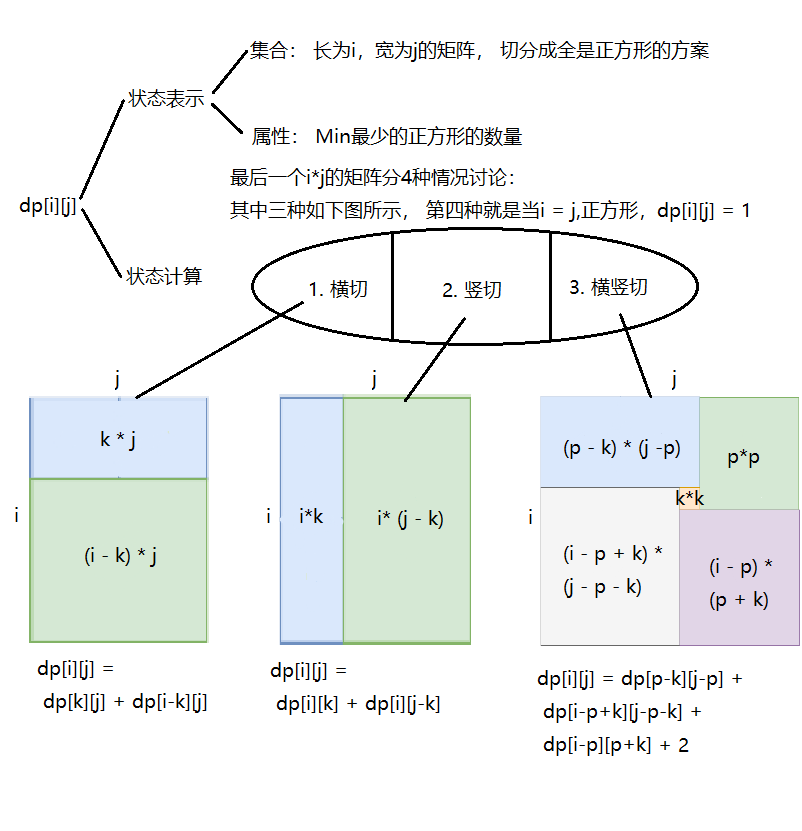
image
时间复杂度：$O(n^4)$
空间复杂度：$O(n^2)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int calMin(int x, int y){
        return x<y?x:y;
    }
    int tilingRectangle(int n, int m) {
        int DP[n+1][m+1];
        memset(DP, 0x3f3f3f3f, sizeof(DP));
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++) {
                if(i==j){ //正方形
                    DP[i][j]=1;
                    continue;
                }

                for(int k=1;k<i;k++){ //横切
                    DP[i][j]=calMin(DP[i][j], DP[k][j]+DP[i-k][j]);
                }

                for(int k=1;k<j;k++){ //竖切
                    DP[i][j]=calMin(DP[i][j], DP[i][k]+DP[i][j-k]);
                }

                for(int p=1;p<=min(i, j);p++){ //横竖切
                    for(int k=1;k<=p;k++){
                        if(p-k<=0||j-p<=0||i-p+k<=0||j-p-k<=0) continue; //不能构成横竖切
                        DP[i][j]=calMin(DP[i][j], DP[p-k][j-p]+DP[i-p+k][j-p-k]+DP[i-p][p+k]+2);
                    }
                }
            }
        }
        return DP[n][m];
    }
};

面试题 08.14. 布尔运算

Description
给定一个布尔表达式和一个期望的布尔结果 result，布尔表达式由 0 (false)、1 (true)、& (AND)、 | (OR) 和 ^ (XOR) 符号组成。实现一个函数，算出有几种可使该表达式得出 result 值的括号方法。
Example
示例 1:
输入: s = “1^0|0|1”, result = 0
输出: 2
解释: 两种可能的括号方法是
1^(0|(0|1))
1^((0|0)|1)

示例 2:
输入: s = “0&0&0&1^1|0”, result = 1
输出: 10
提示：
运算符的数量不超过 19 个
Program
设DP[i][j][0/1]为区间[i,j]结果为0/1的个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    int countEval(string s, int result) {
        int n=s.length();
        int DP[n+1][n+1][2];
        memset(DP, 0, sizeof(DP));
        for(int i=0;i<n;i++){
            if(s[i]=='0'||s[i]=='1') DP[i+1][i+1][s[i]-'0']=1, DP[i+1][i+1][((s[i]-'0')^1)]=0;
        }
        for(int i=n;i>=1;i--){
            if(s[i-1]=='&'||s[i-1]=='|'||s[i-1]=='^') continue;
            for(int j=1;j<=n;j++){
                if(s[j-1]=='&'||s[j-1]=='|'||s[j-1]=='^') continue;
                for(int k=i+1;k<j;k++){
                    if(s[k-1]=='&'){
                        DP[i][j][0]+=DP[i][k-1][0]*DP[k+1][j][0]
                                    +DP[i][k-1][0]*DP[k+1][j][1]
                                    +DP[i][k-1][1]*DP[k+1][j][0];
                        DP[i][j][1]+=DP[i][k-1][1]*DP[k+1][j][1];
                    }else if(s[k-1]=='|'){
                        DP[i][j][0]+=DP[i][k-1][0]*DP[k+1][j][0];
                        DP[i][j][1]+=DP[i][k-1][1]*DP[k+1][j][1]
                                    +DP[i][k-1][0]*DP[k+1][j][1]
                                    +DP[i][k-1][1]*DP[k+1][j][0];
                    }else if(s[k-1]=='^'){
                        DP[i][j][0]+=DP[i][k-1][0]*DP[k+1][j][0]
                                    +DP[i][k-1][1]*DP[k+1][j][1];
                        DP[i][j][1]+=DP[i][k-1][0]*DP[k+1][j][1]
                                    +DP[i][k-1][1]*DP[k+1][j][0];
                    }
                }
            }
        }
        return DP[1][n][result];
    }
};

面试题 17.23. 最大黑方阵

Description
给定一个方阵，其中每个单元(像素)非黑即白。设计一个算法，找出 4 条边皆为黑色像素的最大子方阵。
返回一个数组 [r, c, size] ，其中 r, c 分别代表子方阵左上角的行号和列号，size 是子方阵的边长。若有多个满足条件的子方阵，返回 r 最小的，若 r 相同，返回 c 最小的子方阵。若无满足条件的子方阵，返回空数组。
Example
示例 1:
输入:
[
[1,0,1],
[0,0,1],
[0,0,1]
]
输出: [1,0,2]
解释: 输入中 0 代表黑色，1 代表白色，标粗的元素即为满足条件的最大子方阵

示例 2:
输入:
[
[0,1,1],
[1,0,1],
[1,1,0]
]
输出: [0,0,1]
提示：
matrix.length == matrix[0].length <= 200
Program
动态规划
设down[i][j],right[i][j]分别表示以[i,j]为左上角往下和往右的连续0个数，
那么以[i,j]为左上角的四条边全为0的方形边长radius=k+1，其中k为满足三条件的最大值:
$k<min(down[i][j], right[i][j])且right[i+k][j]>=k+1且down[i][j+k]>=k+1)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    vector<int> findSquare(vector<vector<int>>& matrix) {
        int n=matrix.size();
        int right[n+1][n+1], down[n+1][n+1];
        memset(right, 0, sizeof(right));
        memset(down, 0, sizeof(down));
        int maxRadius=0;
        int r=-1, c=-1;
        for(int i=n-1;i>=0;i--){
            for(int j=n-1;j>=0;j--){
                if(matrix[i][j]==1) continue;
                right[i][j]=down[i][j]=1;
                right[i][j]+=right[i][j+1];
                down[i][j]+=down[i+1][j];
                for(int k=0;k<min(down[i][j], right[i][j]);k++){
                    if(k+1>=maxRadius&&right[i+k][j]>=k+1&&down[i][j+k]>=k){
                        maxRadius=k+1;
                        r=i;
                        c=j;
                    }
                }
            }
        }
        if(maxRadius==0) return {};
        return {r, c, maxRadius};
    }
};

1277. 统计全为 1 的正方形子矩阵

Description
给你一个 m * n 的矩阵，矩阵中的元素不是 0 就是 1，请你统计并返回其中完全由 1 组成的 正方形 子矩阵的个数。
Example
示例 1：
输入：matrix =
[
[0,1,1,1],
[1,1,1,1],
[0,1,1,1]
]
输出：15
解释：
边长为 1 的正方形有 10 个。
边长为 2 的正方形有 4 个。
边长为 3 的正方形有 1 个。
正方形的总数 = 10 + 4 + 1 = 15.

示例 2：
输入：matrix =
[
[1,0,1],
[1,1,0],
[1,1,0]
]
输出：7
解释：
边长为 1 的正方形有 6 个。
边长为 2 的正方形有 1 个。
正方形的总数 = 6 + 1 = 7.

提示：
1 <= arr.length <= 300
1 <= arr[0].length <= 300
0 <= arr[i][j] <= 1
Program
动规
设DP[i][j]为以i,j为右下角的正方形最大正方形边长，则状态转移方程：
当matrix[i][j]==1时，$DP[i][j]=min(DP[i][j-1],min(DP[i-1][j],DP[i-1][j-1]))+1;$
否则，DP[i][j]=0：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int countSquares(vector<vector<int>>& matrix) {
        int m=matrix.size(), n=matrix[0].size();
        int DP[m+1][n+1];
        memset(DP, 0, sizeof(DP));
        int ans=0;
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(matrix[i-1][j-1]==1) DP[i][j]=min(DP[i][j-1],min(DP[i-1][j],DP[i-1][j-1]))+1;
                ans+=DP[i][j];
            }
        }
        return ans;
    }
};

1314. 矩阵区域和

Description
给你一个 m * n 的矩阵 mat 和一个整数 K ，请你返回一个矩阵 answer ，其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和：

  • i - K <= r <= i + K, j - K <= c <= j + K
  • (r, c) 在矩阵内。

Example
示例 1：
输入：mat = [[1,2,3],[4,5,6],[7,8,9]], K = 1
输出：[[12,21,16],[27,45,33],[24,39,28]]

示例 2：
输入：mat = [[1,2,3],[4,5,6],[7,8,9]], K = 2
输出：[[45,45,45],[45,45,45],[45,45,45]]

提示：
m == mat.length
n == mat[i].length
1 <= m, n, K <= 100
1 <= mat[i][j] <= 100
Program
DP
设DP[i][j]为以i,j为右下角的从矩阵左上角开始的矩阵区域和，状态转移方程：
$DP[i][j]=DP[i][j-1]+DP[i-1][j]-DP[i-1][j-1]+mat[i-1][j-1];$
Mat[i][j]就是对应目标值为DP[up][right]-DP[up][left]-DP[down][right]+DP[down][left];
详见代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int m, n;
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int K) {
        m=mat.size(), n=mat[0].size();
        int DP[m+1][n+1]; //多开一维，免得边界判断
        memset(DP, 0, sizeof(DP));
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                DP[i][j]=DP[i][j-1]+DP[i-1][j]-DP[i-1][j-1]+mat[i-1][j-1];
            }
        }
        vector<vector<int>> A(m+1, vector<int>(n+1, 0)); //多开一维，方便边界运算，比如i-K,j-K不在矩阵范围内，可以使用A[0][X]以及A[X][0]
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                int down=(i-K-1<1)?0:i-K-1;
                int up=(i+K>m)?m:i+K;
                int left=(j-K-1<1)?0:j-K-1;
                int right=(j+K>n)?n:j+K;
                A[i][j]=DP[up][right]-DP[up][left]-DP[down][right]+DP[down][left];
                mat[i-1][j-1]=A[i][j];
            }
        }
        return mat;
    }
};

1504. 统计全 1 子矩形

Description
给你一个只包含 0 和 1 的 rows * columns 矩阵 mat ，请你返回有多少个 子矩形 的元素全部都是 1 。
Example
示例 1：
输入：mat = [[1,0,1],
[1,1,0],
[1,1,0]]
输出：13
解释：
有 6 个 1x1 的矩形。
有 2 个 1x2 的矩形。
有 3 个 2x1 的矩形。
有 1 个 2x2 的矩形。
有 1 个 3x1 的矩形。
矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13 。

示例 2：
输入：mat = [[0,1,1,0],
[0,1,1,1],
[1,1,1,0]]
输出：24
解释：
有 8 个 1x1 的子矩形。
有 5 个 1x2 的子矩形。
有 2 个 1x3 的子矩形。
有 4 个 2x1 的子矩形。
有 2 个 2x2 的子矩形。
有 2 个 3x1 的子矩形。
有 1 个 3x2 的子矩形。
矩形数目总共 = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24 。

示例 3：
输入：mat = [[1,1,1,1,1,1]]
输出：21

示例 4：
输入：mat = [[1,0,1],[0,1,0],[1,0,1]]
输出：5

提示：
1 <= rows <= 150
1 <= columns <= 150
0 <= mat[i][j] <= 1
Program
DP
根据之前DP做正方形类似的题目的经验，有时会需要left[i][j]和up[i][j]记录两个方向的边长，这里同样记录以[i,j]为右止点的连续1的长度，那么设DP[i][j]为所求以i,j为右下角的举行个数，明显有：
$DP[i][j]=\sum_{k=i}^{0}(row[k][j])$其中一但row[i][j]==0就终止因为其表示第k行没有1断层了。整个思路就是计算第k层的以[i,j]为右下角的矩形数，(k=i…0)，也就是以第i行为底边[i,j]为右下角，第k行为上边的矩形。
时间复杂度：$O(m^2 n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int numSubmat(vector<vector<int>>& mat) {
        int m=mat.size(), n=mat[0].size();
        int row[m][n];
        memset(row, 0, sizeof(row));
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(mat[i][j]==1) row[i][j]=(j>0?row[i][j-1]:0)+1;
                // cout<<row[i][j]<<" ";
            }
            // cout<<endl;
        }
        int ans=0;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                int width=row[i][j];
                for(int k=i;k>=0&&width>0;k--){
                    width=min(width, row[k][j]);
                    ans+=width;
                }
            }
        }
        return ans;
    }
};

计数DP

62. 不同路径

Description
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。
问总共有多少条不同的路径？
image
例如，上图是一个7 x 3 的网格。有多少可能的路径？
说明：m 和 n 的值均不超过 100。
Example
示例 1:
输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。

  1. 向右 -> 向右 -> 向下
  2. 向右 -> 向下 -> 向右
  3. 向下 -> 向右 -> 向右

示例 2:
输入: m = 7, n = 3
输出: 28
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<int> DP;
        DP.resize(n,0);
        DP[0]=1;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(j>0) DP[j]+=DP[j-1];
            }
        }
        return DP[n-1];
    }
};

63. 不同路径 II

Description
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？
image
网格中的障碍物和空位置分别用 1 和 0 来表示。
说明：m 和 n 的值均不超过 100。
Example
示例 1:
输入:
[
[0,0,0],
[0,1,0],
[0,0,0]
]
输出: 2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：

  1. 向右 -> 向右 -> 向下 -> 向下
  2. 向下 -> 向下 -> 向右 -> 向右

Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        if(obstacleGrid.size()==0) return 0;
        int m=obstacleGrid.size();
        int n=obstacleGrid[0].size();
        vector<long long> DP;
        DP.resize(n, 0);
        DP[0]=1;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(j>0) DP[j]+=DP[j-1];
                if(obstacleGrid[i][j]==1) DP[j]=0;
            }
        }
        return DP[n-1];
    }
};

96. 不同的二叉搜索树

Description
给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？
Example
示例:
输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:

1
2
3
4
5
1         3     3      2      1
 \       /     /      / \      \
  3     2     1      1   3      2
 /     /       \                 \
2     1         2                 3

Program
DP[n]：序列n为节点组成的二叉搜索树的个数
$DP[n]=sum((DP[i-1]*DP[n-i]) for i in range(1, n))$
DP[i-1] 为选择i为根结点下左子树组成的个数，DP[n-i]表示选择i为根结点下右子树组成的个数
边界条件DP[0]=DP[1]=1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int numTrees(int n) {
        vector<int> DP(n+1, 0);
        DP[0]=DP[1]=1;
        //DP[n]=sum((DP[i-1]*DP[n-i]) for i in range(1, n))
        for(int i=2;i<=n;i++){
            for(int j=1;j<=i;j++){
                DP[i]+=DP[j-1]*DP[i-j];
            }
        }
        return DP[n];
    }
};

DP[n]满足卡特兰数！

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int numTrees(int n) {
        vector<long> DP(n+1, 0);
        DP[0]=1;
        for(int i=0;i<n;i++){
            DP[i+1]=DP[i]*2*(2*i+1)/(i+2);
        }
        return DP[n];
    }
};

377. 组合总和 Ⅳ

Description
给定一个由正整数组成且不存在重复数字的数组，找出和为给定目标正整数的组合的个数。
Example
示例:
nums = [1, 2, 3]
target = 4
所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意，顺序不同的序列被视作不同的组合。
因此输出为 7。
Program
暴力就是深搜，动规就是深搜的记忆化搜索翻版，$DP[v]=sum(DP[v-nums[i]]), i\in{[1, n)}$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        if(nums.size()==0&&target!=0) return 0;
        int n=nums.size();
        vector<unsigned long long> DP(target+1, 0);
        DP[0]=1;
        for(int i=1;i<=target;i++){
            for(int v:nums){
                if(i>=v){
                    DP[i]+=DP[i-v];
                }
            }
        }
        return DP[target];
    }
};

576. 出界的路径数

Description
给定一个 m × n 的网格和一个球。球的起始坐标为 (i,j) ，你可以将球移到相邻的单元格内，或者往上、下、左、右四个方向上移动使球穿过网格边界。但是，你最多可以移动 N 次。找出可以将球移出边界的路径数量。答案可能非常大，返回 结果 mod 109 + 7 的值。
Example
示例 1：
输入: m = 2, n = 2, N = 2, i = 0, j = 0
输出: 6
解释: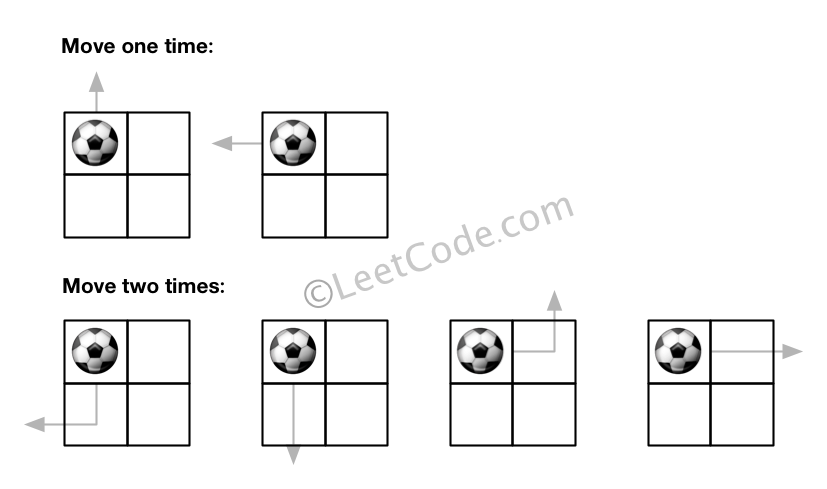
image
示例 2：
输入: m = 1, n = 3, N = 3, i = 0, j = 1
输出: 12
解释: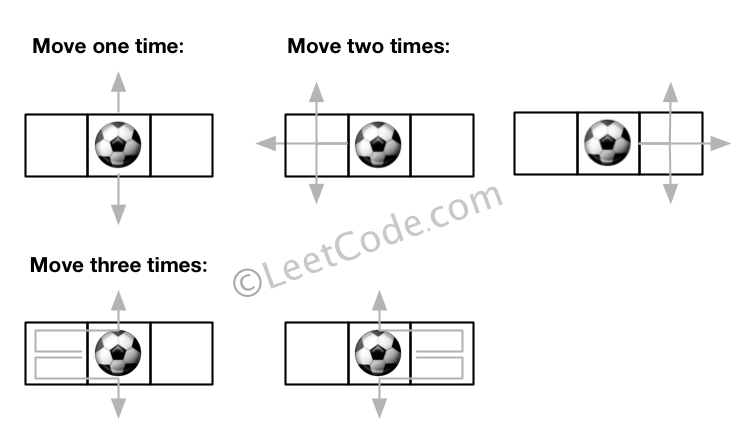
image
说明:
球一旦出界，就不能再被移动回网格内。
网格的长度和高度在 [1,50] 的范围内。
N 在 [0,50] 的范围内。
Program
DP[i][j][v]表示恰好走出v步的路径数！但最后要求总数，肯定包括富裕步数走出边界的情况，所以要累加！
即走1…N步总的结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
public:
    int step[4][2]={
        {1, 0},
        {-1, 0},
        {0, -1},
        {0, 1}
    };
    int mod=1e9+7;
    int findPaths(int m, int n, int N, int i, int j) {
        if(N==0) return 0;
        vector<vector<vector<long long>>> DP(m, vector<vector<long long>>(n, vector<long long>(N+1, 0)));
        for(int i=0;i<m;i++){
            DP[i][0][1]+=1;
            DP[i][n-1][1]+=1;
        }
        for(int i=0;i<n;i++){
            DP[0][i][1]+=1;
            DP[m-1][i][1]+=1;
        }
        for(int v=1;v<=N;v++){
            for(int i=0;i<m;i++){
                for(int j=0;j<n;j++){
                    for(int k=0;k<4;k++){
                        int x=i+step[k][0];
                        int y=j+step[k][1];
                        if(x<0||x>=m||y<0||y>=n) continue;
                        DP[i][j][v]+=DP[x][y][v-1];
                        DP[i][j][v]%=mod;
                    }
                }
            }
        }
        for(int x=1;x<=N;x++){
            DP[i][j][x]+=DP[i][j][x-1];
            DP[i][j][x]%=mod;
        }

        return DP[i][j][N];
    }
};

DP[i][j][v]表示最终结果，可以有步数v富裕！！相比于记忆化搜索，这个慢了。注意先步数循环，注意DP需要四个方位下的数据都先算出来的！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
int step[4][2]={
        {1, 0},
        {-1, 0},
        {0, -1},
        {0, 1}
    };
    int mod=1e9+7;
    int findPaths(int m, int n, int N, int i, int j) {
        if(N==0) return 0;
        vector<vector<vector<long long>>> DP(m, vector<vector<long long>>(n, vector<long long>(N+1, 0)));
        for(int v=1;v<=N;v++){
            for(int i=0;i<m;i++){
                for(int j=0;j<n;j++){
                    for(int k=0;k<4;k++){
                        int x=i+step[k][0];
                        int y=j+step[k][1];
                        if(x<0||x>=m||y<0||y>=n){
                            DP[i][j][v]+=1;
                        }else DP[i][j][v]+=DP[x][y][v-1];
                        DP[i][j][v]%=mod;
                    }
                }
            }
        }
        return DP[i][j][N];
    }
};

记忆化搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    int step[4][2]={
        {1, 0},
        {-1, 0},
        {0, -1},
        {0, 1}
    };
    int mod=1e9+7;
    int findPaths(int m, int n, int N, int i, int j) {
        if(N==0) return 0;
        vector<vector<vector<long long>>> DP(m, vector<vector<long long>>(n, vector<long long>(N+1, -1)));
        return findPath(m,n,N,i,j, DP);
    }
    int findPath(int m, int n, int N,int i, int j, vector<vector<vector<long long>>>& DP){
        if(N<0) return 0;
        if(i<0||i>=m||j<0||j>=n) return 1;
        if(DP[i][j][N]==-1){
            DP[i][j][N]=0;
            for(int k=0;k<4;k++){
                int x=i+step[k][0];
                int y=j+step[k][1];
                DP[i][j][N]+=findPath(m,n,N-1,x, y, DP);
                DP[i][j][N]%=mod;
            }
        }
        return DP[i][j][N];
    }
};

673. 最长递增子序列的个数

Description
给定一个未排序的整数数组，找到最长递增子序列的个数。
Example
示例 1:
输入: [1,3,5,4,7]
输出: 2
解释: 有两个最长递增子序列，分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。

示例 2:
输入: [2,2,2,2,2]
输出: 5
解释: 最长递增子序列的长度是1，并且存在5个子序列的长度为1，因此输出5。
注意: 给定的数组长度不超过 2000 并且结果一定是32位有符号整数。
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int findNumberOfLIS(vector<int>& nums) {
        if(nums.size()==0) return 0;
        int n=nums.size();
        vector<int> DP(n, 1), count(n ,1);
        int maxN=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<i;j++){
                if(nums[i]>nums[j]){
                    if(DP[j]+1==DP[i]) count[i]+=count[j];
                    if(DP[j]+1>DP[i]){
                        DP[i]=DP[j]+1;
                        count[i]=count[j];
                    }
                }
            }
            maxN=max(maxN, DP[i]);
        }
        int ans=0;
        for(int i=0;i<n;i++){
            if(DP[i]==maxN) ans+=count[i];
        }
        return ans;
    }
};

1155. 掷骰子的N种方法

Description
这里有 d 个一样的骰子，每个骰子上都有 f 个面，分别标号为 1, 2, …, f。
我们约定：掷骰子的得到总点数为各骰子面朝上的数字的总和。
如果需要掷出的总点数为 target，请你计算出有多少种不同的组合情况（所有的组合情况总共有 f^d 种），模 10^9 + 7 后返回。
Example
示例 1：
输入：d = 1, f = 6, target = 3
输出：1

示例 2：
输入：d = 2, f = 6, target = 7
输出：6

示例 3：
输入：d = 2, f = 5, target = 10
输出：1

示例 4：
输入：d = 1, f = 2, target = 3
输出：0

示例 5：
输入：d = 30, f = 30, target = 500
输出：222616187

提示：
1 <= d, f <= 30
1 <= target <= 1000
Program
设DP[i][j][t]为前i个骰子在第i个骰子为j，分数为t的总数，则：
$DP[i][j][t]=\sum_{k=1}^{f} DP[i-1][k][t-j]$
时间复杂度：$O(n^5)，n=30$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    const int MOD=1e9+7;
    int numRollsToTarget(int d, int f, int target) {
        if(target<d||target>d*f) return 0;
        int DP[d+1][f+1][d*f+1];
        memset(DP, 0, sizeof(DP));
        for(int i=1;i<=d;i++){
            for(int j=1;j<=f;j++){
                if(i==1){
                    DP[1][j][j]=1;
                    continue;
                }
                for(int t=j;t<=d*f;t++){
                    for(int k=1;k<=f;k++){
                        DP[i][j][t]=(DP[i][j][t]+DP[i-1][k][t-j])%MOD;
                    }
                }
            }
        }
        int ans=0;
        for(int j=1;j<=f;j++){
            ans=(ans+DP[d][j][target])%MOD;
        }
        return ans;
    }
};

设DP[i][j]为前i个骰子总分为j的总数，则：
$DP[i][j]=\sum_{k=1}^{f} DP[i-1][j-k]$
时间复杂度：$O(n^3),n=30$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    const int MOD=1e9+7;
    int numRollsToTarget(int d, int f, int target) {
        if(target<d||target>d*f) return 0;
        int DP[d+1][d*f+1];
        memset(DP, 0, sizeof(DP));
        for(int j=1;j<=f;j++) DP[1][j]=1;
        for(int i=2;i<=d;i++){
            for(int j=i;j<=target;j++){ //j从i开始，因为i个骰子最低得分为i,如果低于i，则总数为0，这里已经初始化过了，不用计算
                for(int k=1;k<=f&&k<=j;k++){
                    DP[i][j]=(DP[i][j]+DP[i-1][j-k])%MOD;
                }
            }
        }
        return DP[d][target];
    }
};

空间优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    const int MOD=1e9+7;
    int numRollsToTarget(int d, int f, int target) {
        if(target<d||target>d*f) return 0;
        int DP[d*f+1];
        memset(DP, 0, sizeof(DP));
        for(int j=1;j<=f;j++) DP[j]=1;
        for(int i=2;i<=d;i++){
            for(int j=target;j>=1;j--){ //注意j从1开始，因为需要初始化每一行DP[j]，下一行会用到上一行的DP[j]，而上一行某些部分应当为0，即必须全部初始化
                DP[j]=0; //每一行记得初始化！
                if(j<i) continue;
                for(int k=1;k<=f&&k<=j;k++){
                    DP[j]=(DP[j]+DP[j-k])%MOD;
                }
            }
        }
        return DP[target];
    }
};

1223. 掷骰子模拟

Description
有一个骰子模拟器会每次投掷的时候生成一个 1 到 6 的随机数。
不过我们在使用它时有个约束，就是使得投掷骰子时，连续 掷出数字 i 的次数不能超过 rollMax[i]（i 从 1 开始编号）。
现在，给你一个整数数组 rollMax 和一个整数 n，请你来计算掷 n 次骰子可得到的不同点数序列的数量。
假如两个序列中至少存在一个元素不同，就认为这两个序列是不同的。由于答案可能很大，所以请返回 模 10^9 + 7 之后的结果。
Example
示例 1：
输入：n = 2, rollMax = [1,1,2,2,2,3]
输出：34
解释：我们掷 2 次骰子，如果没有约束的话，共有 6 * 6 = 36 种可能的组合。但是根据 rollMax 数组，数字 1 和 2 最多连续出现一次，所以不会出现序列 (1,1) 和 (2,2)。因此，最终答案是 36 -2 = 34。

示例 2：
输入：n = 2, rollMax = [1,1,1,1,1,1]
输出：30

示例 3：
输入：n = 3, rollMax = [1,1,1,2,2,3]
输出：181

提示：
1 <= n <= 5000
rollMax.length == 6
1 <= rollMax[i] <= 15
Program
思路
用 dp[i][j][k] 表示第 i 轮掷骰子掷出数字 j 时 j 连续出现 k 次的组合数量。
那么有状态转移如下：
(1)当 j 并非在连续出现时（即 k == 1 时）：

1
2
// j 出现 1 次的组合数等于上一轮投出非数字 j 的所有情况和
dp[i][j][1] = sum(dp[i - 1][l != j][:])

(2)当 j 连续出现 k(k > 1) 次时：

1
2
3
if k <= rollMax[j]:
    // 本轮投出连续出现 k 次数字 j 的情况数量等于：上一轮连续投掷出 k - 1 次 j 的情况数量
    dp[i][j][k] = dp[i - 1][j][k - 1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    const int MOD=1e9+7;
    int dieSimulator(int n, vector<int>& rollMax) {
        int DP[n+1][7][16];
        memset(DP, 0, sizeof(DP));
        for(int i=1;i<=n;i++){
            for(int j=1;j<=6;j++){
                if(i==1){
                    DP[i][j][1]=1;
                    continue;
                }
                //k==1，第一次j
                for(int l=1;l<=6;l++){
                    if(l==j) continue;
                    for(int k=1;k<=15;k++){
                        DP[i][j][1]=(DP[i][j][1]+DP[i-1][l][k])%MOD;
                    }
                }
                //k>1，连续j
                for(int k=2;k<=rollMax[j-1];k++){
                    DP[i][j][k]=DP[i-1][j][k-1];
                }
            }
        }
        int ans=0;
        for(int j=1;j<=6;j++){
            for(int k=1;k<=15;k++){
                ans=(ans+DP[n][j][k])%MOD;
            }
        }
        return ans;
    }
};

面试题 17.06. 2出现的次数

Description
编写一个方法，计算从 0 到 n (含 n) 中数字 2 出现的次数。
Example
示例:
输入: 25
输出: 9
解释: (2, 12, 20, 21, 22, 23, 24, 25)(注意 22 应该算作两次)
提示：
$n <= 10^9$
Program

1
2
3
4
5
6
7
8
9
10
11
以前写过的都忘了。。。
思路：计算每一位2出现的个数！
以13a31一般式子为例，计算百位2的个数
a=3>2时，有200~299,...,13200~13299一共(13+1)×100个2，注意13是前缀！
a=2==2时，有200~299,...,12200~12299以及13200~13231，一共13×100+31+1个数，注意13是前缀，31是后缀
a=1<2时，有200~299,...,12200~12299一共13×100个数！
所以不失一般性：
xxxayyy
a>3时，一共(xxx+1)×len(yyy)
a==2时，一共xxx×len(yyy)+yyy+1
a<2时，一共xxx×len(yyy)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int numberOf2sInRange(int n) {
        long base=1, post=0; //基数、后缀
        int pre=n/10; //前缀数
        int res=n%10; //当前以10*base为基的余数
        int ans=0;
        while(n!=post){
            if(res>2) ans+=(pre+1)*base;
            else if(res==2) ans+=pre*base + post + 1;
            else ans+=pre*base;
            post+=res*base;
            base*=10;
            res=pre%10;
            pre/=10;
        }
        return ans;
    }
};

递推DP

64. 最小路径和

Description
给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。
说明：每次只能向下或者向右移动一步。
Example
示例:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        if(grid.size()==0) return 0;
        int m=grid.size();
        int n=grid[0].size();
        vector<int> DP=grid[0];
        for(int i=1;i<n;i++) DP[i]+=DP[i-1];
        for(int i=1;i<m;i++){
            for(int j=0;j<n;j++){
                if(j>0) DP[j]=min(DP[j], DP[j-1]);
                DP[j]+=grid[i][j];
            }
        }
        return DP[n-1];
    }
};

70. 爬楼梯

Description
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
注意：给定 n 是一个正整数。
Example
示例 1：
输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。

  1. 1 阶 + 1 阶
  2. 2 阶

示例 2：
输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。

  1. 1 阶 + 1 阶 + 1 阶
  2. 1 阶 + 2 阶
  3. 2 阶 + 1 阶

Program

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int climbStairs(int n) {
        vector<int> DP;
        DP.resize(n+1);
        DP[0]=DP[1]=1;
        for(int i=2;i<=n;i++){
            DP[i]=DP[i-1]+DP[i-2];
        }
        return DP[n];
    }
};

1423. 可获得的最大点数

Description
几张卡牌 排成一行，每张卡牌都有一个对应的点数。点数由整数数组 cardPoints 给出。
每次行动，你可以从行的开头或者末尾拿一张卡牌，最终你必须正好拿 k 张卡牌。
你的点数就是你拿到手中的所有卡牌的点数之和。
给你一个整数数组 cardPoints 和整数 k，请你返回可以获得的最大点数。
Example
示例 1：
输入：cardPoints = [1,2,3,4,5,6,1], k = 3
输出：12
解释：第一次行动，不管拿哪张牌，你的点数总是 1 。但是，先拿最右边的卡牌将会最大化你的可获得点数。最优策略是拿右边的三张牌，最终点数为 1 + 6 + 5 = 12 。

示例 2：
输入：cardPoints = [2,2,2], k = 2
输出：4
解释：无论你拿起哪两张卡牌，可获得的点数总是 4 。

示例 3：
输入：cardPoints = [9,7,7,9,7,7,9], k = 7
输出：55
解释：你必须拿起所有卡牌，可以获得的点数为所有卡牌的点数之和。

示例 4：
输入：cardPoints = [1,1000,1], k = 1
输出：1
解释：你无法拿到中间那张卡牌，所以可以获得的最大点数为 1 。

示例 5：
输入：cardPoints = [1,79,80,1,1,1,200,1], k = 3
输出：202

提示：
1 <= cardPoints.length <= 10^5
1 <= cardPoints[i] <= 10^4
1 <= k <= cardPoints.length
Program
常规dfs/动规
无论dfs还是动规都超时超限。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    // const int inf=0x3f3f3f3f;
    int vis[100000][100000][100000]={-1};
    int dfs(vector<int>& cardPoints, int i, int j, int k){
        if(i>j) return 0;
        if(k==0) return 0;
        if(vis[i][j][k]!=-1) return vis[i][j][k];
        int ans=0;
        ans=max(cardPoints[i]+dfs(cardPoints, i+1, j, k-1), cardPoints[j]+dfs(cardPoints, i, j-1, k-1));
        vis[i][j][k]=ans;
        return ans;
    }
    int maxScore(vector<int>& cardPoints, int k) {
        return dfs(cardPoints, 0, cardPoints.size()-1, k);
    }
};

动规变形
考虑拿k个，无非数组前后总和k个，可以是：
前0，后1
…
前k，后0
即动规递推公式：$DP[n]=max(preSum[i]+preSum[n]-preSum[n-(k-i)]),i=0,1,2,…,k$
时间复杂度：$O(n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int maxScore(vector<int>& cardPoints, int k) {
        int n=cardPoints.size();
        int preSum[n+1];
        memset(preSum, 0, sizeof(preSum));
        for(int i=0;i<n;i++){
            preSum[i+1]+=cardPoints[i];
            if(i>0) preSum[i+1]+=preSum[i];
        }
        int ans=0;
        for(int i=0;i<=k;i++){
            ans=max(ans, preSum[i]+preSum[n]-preSum[n-(k-i)]);
        }
        return ans;
    }
};

1621. 大小为 K 的不重叠线段的数目

Description
给你一维空间的 n 个点，其中第 i 个点（编号从 0 到 n-1）位于 x = i 处，请你找到 恰好 k 个不重叠 线段且每个线段至少覆盖两个点的方案数。线段的两个端点必须都是 整数坐标 。这 k 个线段不需要全部覆盖全部 n 个点，且它们的端点 可以 重合。
请你返回 k 个不重叠线段的方案数。由于答案可能很大，请将结果对 109 + 7 取余 后返回。
Example
示例 1：
输入：n = 4, k = 2
输出：5
解释：
如图所示，两个线段分别用红色和蓝色标出。
上图展示了 5 种不同的方案 {(0,2),(2,3)}，{(0,1),(1,3)}，{(0,1),(2,3)}，{(1,2),(2,3)}，{(0,1),(1,2)} 。

示例 2：
输入：n = 3, k = 1
输出：3
解释：总共有 3 种不同的方案 {(0,1)}, {(0,2)}, {(1,2)} 。

示例 3：
输入：n = 30, k = 7
输出：796297179
解释：画 7 条线段的总方案数为 3796297200 种。将这个数对 109 + 7 取余得到 796297179 。

示例 4：
输入：n = 5, k = 3
输出：7

示例 5：
输入：n = 3, k = 2
输出：1

提示：
2 <= n <= 1000
1 <= k <= n-1
Program
动态规划
基于之前做过题目的思考，DP[i]为最终答案的话，那么肯定得考虑i是否为最后一条线段的终点，定义就变成了DP[i][2]，DP[i][0]表示最后一条线段不以i为结尾，DP[i][1]表示最后一条线段以i为结尾，但是这还不够，一般来讲需要以最后一条路径DP[0,k],DP[i,j]来递推，类似于单词拆分。但DP[i][j][0]再加上线段数量DP[I][J][K][2]复杂度过高，那么可以考虑类似LCP 秋叶收藏集的做法：
设DP[i][j][0]表示[0..i]构造了j条线段且最后一条线段不以i为结尾的方案数，DP[i][j][1]表示[0…i]构造了j条线段且最后一条线段以i为结尾的方案数
状态转移方程：
（1）$DP[i][j][0]=DP[i-1][j][0]+D[i-1][j][1]$
（2）最后一条线段长度为1
$DP[i][j][1]=DP[i-1][j-1][0]+DP[i-1][j-1][1]$
最后一条线段长度大于1
$DP[i][j][1]+=DP[i-1][j][1];
时间复杂度：$O(nk)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    const int MOD=1e9+7;
    int dp[1001][1001][2];
    int numberOfSets(int n, int k) {
        memset(dp, 0, sizeof(dp));
        dp[0][0][0]=1, dp[0][0][1]=0;
        for(int i=1;i<n;i++){
            for(int j=0;j<=k;j++){
                dp[i][j][0]=(dp[i-1][j][0]+dp[i-1][j][1])%MOD;
                dp[i][j][1]=dp[i-1][j][1];
                if(j>0){
                    dp[i][j][1]+=dp[i-1][j-1][0];
                    dp[i][j][1]%=MOD;
                    dp[i][j][1]+=dp[i-1][j-1][1];
                    dp[i][j][1]%=MOD;
                }
            }
        }
        return (dp[n-1][k][0]+dp[n-1][k][1])%MOD;
    }
};

背包DP

322. 零钱兑换

Description
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。
Example
示例 1:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1

示例 2:
输入: coins = [2], amount = 3
输出: -1
Program
DP[m][i]=min{DP[m][i-1], DP[m-v[i]][i]+1}，注意边界：DP[0][i]=0, DP[m][0]=inf if m<v[i] else DP[m-v[i]][i]+1;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        if(coins.size()==0) return -1;
        int n=coins.size();
        int** DP=new int*[amount+1];
        for(int i=0;i<amount+1;i++) DP[i]=new int[n];
        for(int m=0;m<amount+1;m++){
            for(int i=0;i<n;i++){
                if(m==0){
                    DP[m][i]=0;
                    continue;
                }
                if(i==0){
                    if(m>=coins[i]) DP[m][i]=DP[m-coins[i]][i]+1;
                    else DP[m][i]=0X3f3f3f3f;
                    continue;
                }
                if(m>=coins[i]) DP[m][i]=min(DP[m][i-1], DP[m-coins[i]][i]+1);
                else DP[m][i]=DP[m][i-1];
            }
        }
        return (DP[amount][n-1]>=0x3f3f3f3f)?-1:DP[amount][n-1];
    }
};

$DP[m]=1+min(DP[m-c_i]+1), i\in{[1, k]}$，边界DP[0]=0;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        if(coins.size()==0) return -1;
        int n=coins.size();
        vector<int> DP(amount+1, 0x3f3f3f3f);
        DP[0]=0;
        for(int m=0;m<amount+1;m++){
            for(int w:coins){
                if(w<=m) DP[m]=min(DP[m], DP[m-w]+1);
            }
        }
        return (DP[amount]>=0x3f3f3f3f)?-1:DP[amount];
    }
};

416. 分割等和子集

Description
给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。
注意:
每个数组中的元素不会超过 100
数组的大小不会超过 200
Example
示例 1:
输入: [1, 5, 11, 5]
输出: true
解释: 数组可以分割成 [1, 5, 5] 和 [11].

示例 2:
输入: [1, 2, 3, 5]
输出: false
解释: 数组不能分割成两个元素和相等的子集.
Program
0-1背包，只要满足整个数组和的一半，取或不取就行了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int ans=0;
        int n=nums.size();
        for(int x:nums) ans+=x;
        if((ans&1)!=0) return false;
        ans/=2;
        vector<vector<bool>> DP(n);
        for(int i=0;i<n;i++) DP[i].resize(ans+1, false);
        for(int i=0;i<n;i++){
            for(int v=0;v<=ans;v++){
                if(v==0){
                    DP[i][v]=true;
                    continue;
                }
                if(i!=0&&v>=nums[i]) DP[i][v]=DP[i-1][v]||DP[i-1][v-nums[i]];
                else if(i!=0) DP[i][v]=DP[i-1][v];
            }
        }
        return DP[n-1][ans];
    }
};

空间优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int ans=0;
        int n=nums.size();
        for(int x:nums) ans+=x;
        if((ans&1)!=0) return false;
        ans/=2;
        vector<bool> DP(ans+1, false);
        DP[0]=true;
        for(int i=1;i<n;i++){
            for(int v=ans;v>=nums[i];v--){
                DP[v]=DP[v]||DP[v-nums[i]];
            }
        }
        return DP[ans];
    }
};

474. 一和零

Description
在计算机界中，我们总是追求用有限的资源获取最大的收益。
现在，假设你分别支配着 m 个 0 和 n 个 1。另外，还有一个仅包含 0 和 1 字符串的数组。
你的任务是使用给定的 m 个 0 和 n 个 1 ，找到能拼出存在于数组中的字符串的最大数量。每个 0 和 1 至多被使用一次。
注意:
给定 0 和 1 的数量都不会超过 100。
给定字符串数组的长度不会超过 600。
Example
示例 1:
输入: Array = {“10”, “0001”, “111001”, “1”, “0”}, m = 5, n = 3
输出: 4
解释: 总共 4 个字符串可以通过 5 个 0 和 3 个 1 拼出，即 “10”,”0001”,”1”,”0” 。

示例 2:
输入: Array = {“10”, “0”, “1”}, m = 1, n = 1
输出: 2
解释: 你可以拼出 “10”，但之后就没有剩余数字了。更好的选择是拼出 “0” 和 “1” 。
Program
①暴力
超时

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    int maxn=0;
    int len;
    void find(vector<int>& zeros, vector<int>& ones, int i, int num, int m, int n){
        if(i==len){
            maxn=max(maxn, num);
            return;
        }
        if(zeros[i]<=m&&ones[i]<=n) find(zeros, ones, i+1, num+1, m-zeros[i], n-ones[i]);
        find(zeros, ones, i+1, num, m, n);
    }
    int findMaxForm(vector<string>& strs, int m, int n) {
        if(strs.size()==0) return 0;
        len=strs.size();
        vector<int> zeros(len, 0), ones(len, 0);
        for(int i=0;i<len;i++){
            string str=strs[i];
            for(int j=0;j<str.length();j++){
                if(str[j]=='1') ones[i]++;
                else zeros[i]++;
            }
        }
        find(zeros, ones, 0, 0, m, n);
        return maxn;
    }
};

②DP
0-1背包，$DP[i][m][n]=max(1+DP[i-1][m-zeros[i]][n-ones[i]], DP[i-1][m][n])$，注意边界

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        if(strs.size()==0) return 0;
        int len=strs.size();
        vector<int> zeros(len, 0), ones(len, 0);
        for(int i=0;i<len;i++){
            string str=strs[i];
            for(int j=0;j<str.length();j++){
                if(str[j]=='1') ones[i]++;
                else zeros[i]++;
            }
        }
        vector<vector<vector<int>>> DP(len);
        for(int i=0;i<len;i++){
            DP[i].resize(m+1);
            for(int j=0;j<m+1;j++) DP[i][j].resize(n+1, 0);
        }
        for(int i=0;i<len;i++){
            for(int j=0;j<=m;j++){
                for(int k=0;k<=n;k++){
                    if(i==0){
                        if(j>=zeros[i]&&k>=ones[i]) DP[i][j][k]=1;
                        continue;
                    }
                    if(j>=zeros[i]&&k>=ones[i]){
                        DP[i][j][k]=max(1+DP[i-1][j-zeros[i]][k-ones[i]], DP[i-1][j][k]);
                    }else{
                        DP[i][j][k]=DP[i-1][j][k];
                    }
                }
            }
        }
        return DP[len-1][m][n];
    }
};

状态压缩

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        if(strs.size()==0) return 0;
        int len=strs.size();
        vector<int> zeros(len, 0), ones(len, 0);
        for(int i=0;i<len;i++){
            string str=strs[i];
            for(int j=0;j<str.length();j++){
                if(str[j]=='1') ones[i]++;
                else zeros[i]++;
            }
        }
        vector<vector<int>> DP(m+1);
        for(int i=0;i<m+1;i++) DP[i].resize(n+1, 0);
        for(int i=0;i<len;i++){
            for(int j=m;j>=0;j--){
                for(int k=n;k>=0;k--){
                    if(zeros[i]<=j&&ones[i]<=k){
                        DP[j][k]=max(1+DP[j-zeros[i]][k-ones[i]], DP[j][k]);
                    }              
                }
            }
        }
        return DP[m][n];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        int len = strs.size();
        vector<vector<int> > DP(m + 1, vector<int>(n + 1, 0));
        for(int i = 0; i < len; ++i){
            int zeros = 0;
            int ones = 0;
            for(int j=0;j<strs[i].size();++j){
                if(strs[i][j] == '1') ++ones;
                else ++zeros;
            }
            for(int j = m; j >= zeros; --j){
                for(int k = n; k >= ones; --k){
                    DP[j][k] = max(1 + DP[j-zeros][k-ones], DP[j][k]);             
                }
            }
        }
        return DP[m][n];
    }
};

494. 目标和

Description
给定一个非负整数数组，a1, a2, …, an, 和一个目标数，S。现在你有两个符号 + 和 -。对于数组中的任意一个整数，你都可以从 + 或 -中选择一个符号添加在前面。
返回可以使最终数组和为目标数 S 的所有添加符号的方法数。
Example
示例 1:
输入: nums: [1, 1, 1, 1, 1], S: 3
输出: 5
解释:
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3

一共有5种方法让最终目标和为3。
注意:
数组非空，且长度不会超过20。
初始的数组的和不会超过1000。
保证返回的最终结果能被32位整数存下。
Program
①暴力

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int ans=0;
    void helper(vector<int>&nums, int i, int S, int sum){
        if(i==nums.size()){
            if(sum==S){
                ans++;
            }
            return;
        }
        helper(nums, i+1, S, sum+nums[i]);
        helper(nums, i+1, S, sum-nums[i]);
    }
    int findTargetSumWays(vector<int>& nums, int S) {
        helper(nums, 0, S, 0);
        return ans;
    }
};

②DP
类似于背包问题，设DP[i][j]为0…i中结果为j的个数，那么DP[i][j]=DP[i-1][j-nums[i]]+DP[i-1][j+nums[i]]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:

    int findTargetSumWays(vector<int>& nums, int S) {
        int n=nums.size();
        int sum=0;
        for(int x:nums) sum+=x;
        if(S>sum) return 0; //特判
        int t=2*sum+1;
        vector<vector<int>> DP(n, vector<int>(t, 0));
        for(int i=0;i<n;i++){
            for(int j=0;j<t;j++){
                if(i==0){
                    if(j==sum-nums[i]) DP[i][j]+=1; //注意sum-nums[i]可能等于sum+nums[i]
                    if(j==sum+nums[i]) DP[i][j]+=1;
                    continue;
                }
                if(j-nums[i]>=0&&j+nums[i]<t) DP[i][j]=DP[i-1][j-nums[i]]+DP[i-1][j+nums[i]];
                else if(j-nums[i]>=0) DP[i][j]=DP[i-1][j-nums[i]];
                else if(j+nums[i]<t) DP[i][j]=DP[i-1][j+nums[i]];
            }
        }
        return DP[n-1][sum+S];
    }
};

③DP优化
DP[i][j]=DP[i-1][j-nums[i]]+DP[i-1][j+nums[i]]只与前一行有关，所以只需要两个一维数组即可！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:

    int findTargetSumWays(vector<int>& nums, int S) {
        int n=nums.size();
        int sum=0;
        for(int x:nums) sum+=x;
        if(S>sum) return 0; //特判
        int t=2*sum+1;
        vector<int> DP(t, 0), preDP(t, 0);
        for(int i=0;i<n;i++){
            for(int j=0;j<t;j++){
                if(i==0){
                    if(j==sum-nums[i]) DP[j]+=1; //注意sum-nums[i]可能等于sum+nums[i]
                    if(j==sum+nums[i]) DP[j]+=1;
                    continue;
                }
                if(j-nums[i]>=0&&j+nums[i]<t) DP[j]=preDP[j-nums[i]]+preDP[j+nums[i]];
                else if(j-nums[i]>=0) DP[j]=preDP[j-nums[i]];
                else if(j+nums[i]<t) DP[j]=preDP[j+nums[i]];
            }
            preDP=DP;
        }
        return DP[sum+S];
    }
};

面试题 08.11. 硬币

Description
硬币。给定数量不限的硬币，币值为25分、10分、5分和1分，编写代码计算n分有几种表示法。(结果可能会很大，你需要将结果模上1000000007)
Example
示例1:
输入: n = 5
输出：2
解释: 有两种方式可以凑成总金额:
5=5
5=1+1+1+1+1
示例2:
输入: n = 10
输出：4
解释: 有四种方式可以凑成总金额:
10=10
10=5+5
10=5+1+1+1+1+1
10=1+1+1+1+1+1+1+1+1+1

说明：
注意:
你可以假设：
0 <= n (总金额) <= 1000000
Program
典型动规，DP[m][i]=DP[m][i-1]+DP[m-w[i]][i],边界DP[0][i]=1；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    const int MOD=1e9+7;
    int waysToChange(int n) {
        int w[5]={0, 25, 10, 5, 1};
        int DP[n+1][5];
        memset(DP, 0, sizeof(DP));
        //vector<vector<int>> DP(n+1, vector<int>(5, 0));
        for(int i=1;i<=4;i++) DP[0][i]=1;
        for(int m=1;m<=n;m++){
            for(int i=1;i<=4;i++){
                DP[m][i]=DP[m][i-1]%MOD;
                if(m>=w[i])DP[m][i]=(DP[m][i-1]+DP[m-w[i]][i])%MOD;
            }
        }
        return DP[n][4];
    }
};

1049. 最后一块石头的重量 II

Description
有一堆石头，每块石头的重量都是正整数。
每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：
如果 x == y，那么两块石头都会被完全粉碎；
如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。
最后，最多只会剩下一块石头。返回此石头最小的可能重量。如果没有石头剩下，就返回 0。
Example
示例：
输入：[2,7,4,1,8,1]
输出：1
解释：
组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

提示：
1 <= stones.length <= 30
1 <= stones[i] <= 1000
Program
0-1背包问题
此题要求最后剩余石头重量最小，那么可以考虑将石头分成两堆，使得两堆的和尽可能接近，所以类似于背包容量为$sum/2$，尽可能装满，最后$sum-DP[n-1][target] * 2$就是答案。
$DP[i][j]$代表前i种已经出现的石头，背包容量为j的情况下，能得到的最大值。
$DP[i][j]=max(DP[i-1][j],DP[i-1][j-stones[i]]+stones[i]);$
注意边界；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int lastStoneWeightII(vector<int>& stones) {
        int n=stones.size();
        int sum=0;
        for(int x:stones) sum+=x;
        int target=sum/2;
        int DP[n+1][target+1];
        memset(DP, 0, sizeof(DP));
        for(int i=1;i<=n;i++){
            for(int j=1;j<=target;j++){
                if(j<stones[i-1]) DP[i][j]=DP[i-1][j];
                else DP[i][j]=max(DP[i-1][j], DP[i-1][j-stones[i-1]]+stones[i-1]);
            }
        }
        return sum-DP[n][target]*2;
    }
};

博弈DP

464. 我能赢吗

Description
在 “100 game” 这个游戏中，两名玩家轮流选择从 1 到 10 的任意整数，累计整数和，先使得累计整数和达到 100 的玩家，即为胜者。
如果我们将游戏规则改为 “玩家不能重复使用整数” 呢？
例如，两个玩家可以轮流从公共整数池中抽取从 1 到 15 的整数（不放回），直到累计整数和 >= 100。
给定一个整数 maxChoosableInteger （整数池中可选择的最大数）和另一个整数 desiredTotal（累计和），判断先出手的玩家是否能稳赢（假设两位玩家游戏时都表现最佳）？
你可以假设 maxChoosableInteger 不会大于 20， desiredTotal 不会大于 300。
Example
示例：
输入：
maxChoosableInteger = 10
desiredTotal = 11
输出：
false
解释：
无论第一个玩家选择哪个整数，他都会失败。
第一个玩家可以选择从 1 到 10 的整数。
如果第一个玩家选择 1，那么第二个玩家只能选择从 2 到 10 的整数。
第二个玩家可以通过选择整数 10（那么累积和为 11 >= desiredTotal），从而取得胜利.
同样地，第一个玩家选择任意其他整数，第二个玩家都会赢。
Program
DP[num][total]=!DP[num|i][total-i] if i<total else 1;
num用二进制表示共有maxChoosableInteger位，选择了i则其第i-1为数字为1，表示已选。
DP[num][total]表示当前选取的num组合下先手在total下的输赢情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
private:
    bool helper(vector<int>& vis, int num, int mvalue, int total){
        if(vis[num]!=-1) return vis[num];

        for(int i=0;i<mvalue;i++){
            int cur=(1<<i); //选择i+1
            if((num&cur)) continue;
            if(i+1>=total){
                vis[num]=1;
                break;
            }
            bool next=helper(vis, (num|cur), mvalue, total-i-1);
            if(next==false){
                vis[num]=1;
                break;
            }
        }
        if(vis[num]==-1) vis[num]=0;
        return vis[num];
    }
public:
    bool canIWin(int maxChoosableInteger, int desiredTotal) {
        if((maxChoosableInteger*(maxChoosableInteger+1)/2)<desiredTotal) return false;
        vector<int> vis((1<<maxChoosableInteger)-1, -1); //-1没计算，0和1代表计算后不能赢和能赢
        int num=0;
        return helper(vis, num, maxChoosableInteger, desiredTotal);
    }
};

486. 预测赢家

Description
给定一个表示分数的非负整数数组。 玩家1从数组任意一端拿取一个分数，随后玩家2继续从剩余数组任意一端拿取分数，然后玩家1拿，……。每次一个玩家只能拿取一个分数，分数被拿取之后不再可取。直到没有剩余分数可取时游戏结束。最终获得分数总和最多的玩家获胜。
给定一个表示分数的数组，预测玩家1是否会成为赢家。你可以假设每个玩家的玩法都会使他的分数最大化。
Example
示例 1:
输入: [1, 5, 2]
输出: False
解释: 一开始，玩家1可以从1和2中进行选择。
如果他选择2（或者1），那么玩家2可以从1（或者2）和5中进行选择。如果玩家2选择了5，那么玩家1则只剩下1（或者2）可选。
所以，玩家1的最终分数为 1 + 2 = 3，而玩家2为 5。
因此，玩家1永远不会成为赢家，返回 False。

示例 2:
输入: [1, 5, 233, 7]
输出: True
解释: 玩家1一开始选择1。然后玩家2必须从5和7中进行选择。无论玩家2选择了哪个，玩家1都可以选择233。
最终，玩家1（234分）比玩家2（12分）获得更多的分数，所以返回 True，表示玩家1可以成为赢家。
注意:
1 <= 给定的数组长度 <= 20.
数组里所有分数都为非负数且不会大于10000000。
如果最终两个玩家的分数相等，那么玩家1仍为赢家。
Program
博弈论还是不会，太菜了…
①暴力深搜

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
	bool PredictTheWinner(vector<int>& nums) {
		return helper(0, nums.size() - 1, 0, 0, true, nums);
	}
    bool helper(int left, int right, int score_A, int score_B, bool isA_B, vector<int>& nums){
        if(left>right){
            return score_A>=score_B;  //平局也算A胜
        }
        if(isA_B){ //A无论选左还是右，满足一项即可
            bool bL=helper(left+1, right, score_A+nums[left], score_B, !isA_B, nums);
            bool bR=helper(left, right-1, score_A+nums[right], score_B, !isA_B, nums);
            return (bL||bR);
        }else{ //B只有左右都满足才能保证A胜
            bool bL=helper(left+1, right, score_A, score_B+nums[left], !isA_B, nums);
            bool bR=helper(left, right-1, score_A, score_B+nums[right], !isA_B, nums);
            return (bL&&bR);
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
	bool PredictTheWinner(vector<int>& nums) {
        return helper(nums, 0, nums.size()-1, 1) >= 0;
	}
    int helper(vector<int>& nums, int left, int right, int factor){
        if(left==right) return factor*nums[left];
        int a=factor*nums[left]+helper(nums, left+1, right, -factor);
        int b=factor*nums[right]+helper(nums,left, right-1, -factor);
        return (factor==1)?max(a, b):min(a, b);  //对弈双方都希望利益最大化，先手来说，差越大越好，反手来说，差越小越好。
    }
};

②DP
设DP[i][j]表示选择了nums[i, j]后两个对手分数之差（这个是关键，博弈论关键找到一个联系点才能统一！），
$DP[i][j]=max(nums[i]-DP[i+1][j], nums[j]-DP[i][j-1])$ 注意体会！两个对手状态统一于DP，逆向思维，由里向外
例如：[1, 5, 2, 7]
A:1
B:5
A:2
B:7
差为1-5+2-7=1-[5-(2-7)]
可以发现，差本来是摆动的，全部可以转成减法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
	bool PredictTheWinner(vector<int>& nums) {
        if(nums.size()==0) return true;
        int n=nums.size();
		    vector<vector<int>> DP(n, vector<int>(n, 0));
        for(int i=0;i<n;i++){
            DP[i][i]=nums[i];
        }
        for(int len=2;len<=n;len++){
            for(int i=0;i+len-1<n;i++){
                int j=i+len-1;
                DP[i][j]=max(nums[i]-DP[i+1][j], nums[j]-DP[i][j-1]);
            }
        }
        return DP[0][n-1]>=0;
	}
};

记忆化搜索
helper记录先手在[left,right]下的最高得分，所以递推公式：
score=max(sum-helper(left+1, right, sum-nums[left]), sum-helper(left, right-1, sum-nums[right]));
即先手在[left,right]的最高得分，与两种情况有关：
①先手选择nums[left]，则其最高得分为sum-helper(left+1,right, sum-nums[left]),其中helper(left+1,right,sum-nums[left])为后手在[left+1, right]区间上先手的最高得分！
②同理，先手选择nums[right]，则其最高得分为sum-helper(left, right-1, sum-nums[right])，其中helper(left, right-1, sum-nums[right])为后手在[left, right-1]区间上先手的最高得分！
最后判断先手在[left, right]上的最高得分是否超过floor((sum+1)/2)即可。
由于存在重复计算，所以需要vis[left][right]记录当前计算的区间[left, right]的结果，避免重复计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int n;
    vector<vector<int>> vis;
    int helper(vector<int>& nums, int left, int right, int sum){
        if(left>right) return 0;
        if(vis[left][right]!=-1) return vis[left][right];
        int score1=sum-helper(nums, left+1, right, sum-nums[left]);
        int score2=sum-helper(nums, left, right-1, sum-nums[right]);
        int score=max(score1, score2);
        vis[left][right]=score;
        return vis[left][right];
    }
    bool PredictTheWinner(vector<int>& nums) {
        n=nums.size();
        int sum=accumulate(nums.begin(), nums.end(), 0);
        vis.resize(n, vector<int>(n, -1));
        int score=helper(nums, 0, n-1, sum);
        return score>=(sum+1)/2;
    }
};

DP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    bool PredictTheWinner(vector<int>& nums) {
        int n=nums.size();
        int DP[n+1][n+1];
        int preSum[n+1];
        memset(DP, 0, sizeof(DP));
        memset(preSum, 0, sizeof(preSum));
        for(int i=1;i<=n;i++){
            preSum[i]+=preSum[i-1]+nums[i-1];
            DP[i][i]=preSum[i]-preSum[i-1]; //i==j时特判
        }
        for(int i=n;i>=1;i--){
            for(int j=i+1;j<=n;j++){
                DP[i][j]=max(preSum[j]-preSum[i-1]-DP[i+1][j],
                             preSum[j]-preSum[i-1]-DP[i][j-1]);
            }
        }
        return DP[1][n]>=(preSum[n]+1)/2;
    }
};

1140. 石子游戏 II

Description
亚历克斯和李继续他们的石子游戏。许多堆石子 排成一行，每堆都有正整数颗石子 piles[i]。游戏以谁手中的石子最多来决出胜负。
亚历克斯和李轮流进行，亚历克斯先开始。最初，M = 1。
在每个玩家的回合中，该玩家可以拿走剩下的 前 X 堆的所有石子，其中 1 <= X <= 2M。然后，令 M = max(M, X)。
游戏一直持续到所有石子都被拿走。
假设亚历克斯和李都发挥出最佳水平，返回亚历克斯可以得到的最大数量的石头。
Example
示例：
输入：piles = [2,7,9,4,4]
输出：10
解释：
如果亚历克斯在开始时拿走一堆石子，李拿走两堆，接着亚历克斯也拿走两堆。在这种情况下，亚历克斯可以拿到 2 + 4 + 4 = 10 颗石子。
如果亚历克斯在开始时拿走两堆石子，那么李就可以拿走剩下全部三堆石子。在这种情况下，亚历克斯可以拿到 2 + 7 = 9 颗石子。
所以我们返回更大的 10。

提示：
1 <= piles.length <= 100
1 <= piles[i] <= 10 ^ 4
Program
思路：
本题难点在于理解两者都发挥“最佳水平”，“最佳水平”在于，每当轮到自己拿石子的时候，要在后继的所有状态中，选择对自己最有利的，那么也就是要遍历后继的所有状态，并选择一个最优解。我们设 dfs(i, M) 表示，当从第 i 堆石子开始拿，允许拿 M <= x <= 2 * M 时，在剩余石子中所能拿到的最大值，那么我们最终要返回的结果就是 dfs(0, 1)。搜索状态时，我们要遵循以下几个原则：

  • 如果 i >= n，那么说明石子都已经拿完，直接返回 0；
  • 如果 i + M * 2 >= n，那么说明可以把剩余石子一起拿到，就可以直接返回剩余石子的数目 sum(piles[i:])；
  • 如果不属于以上两种情况，那么我们需要遍历 1 <= x <= 2 * M，求剩余的最小 dfs(i + x, max(x, M))，也就是自己拿多少的时候，对手拿的石子最少（由于剩余石子数固定，那么最小化对手石子数，就是最大化自己的石子数）。
    为了防止重复搜索，可以采用记忆化的方法。为了快速求剩余石子数目，可以提前处理后缀和。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    class Solution {
    public:
        vector<int> sum;
        map<pair<int,int>, int> vis;
        int dfs(vector<int>& piles, int n, int start, int m){
            if(vis.find(pair<int,int>(start, m))!=vis.end()) return vis[pair<int,int>(start, m)];
            if(start>=n) return 0;
            if(start+2*m>=n) return sum[start];
            int best=0;
            for(int x=0;x<2*m;x++){
                best=max(best, sum[start]-dfs(piles, n, start+x+1, max(x+1,m)));
            }
            vis[pair<int,int>(start, m)]=best;
            return best;
        }
        int stoneGameII(vector<int>& piles) {
            int n=piles.size();
            sum.resize(n, 0);
            for(int i=n-1;i>=0;i--){
                sum[i]=piles[i];
                if(i+1<=n-1)sum[i]+=sum[i+1];
            }
            return dfs(piles, n, 0, 1);
        }
    };
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    class Solution {
    public:
        int stoneGameII(vector<int>& piles) {
            int n=piles.size();
            int DP[n][n+1];
            memset(DP, 0, sizeof(DP));
            int sum=0;
            for(int i=n-1;i>=0;i--){
                sum+=piles[i];
                for(int m=1;m<=n;m++){
                    if(i+2*m>=n){
                        DP[i][m]=sum;
                        continue;
                    }
                    for(int x=0;x<2*m&&i+x<n;x++){
                        DP[i][m]=max(DP[i][m], sum-DP[i+x+1][max(x+1,m)]);
                    }
                }  
            }
            return DP[0][1];
        }
    };

    292. Nim 游戏

Description
你和你的朋友，两个人一起玩 Nim 游戏：桌子上有一堆石头，每次你们轮流拿掉 1 - 3 块石头。 拿掉最后一块石头的人就是获胜者。你作为先手。
你们是聪明人，每一步都是最优解。 编写一个函数，来判断你是否可以在给定石头数量的情况下赢得游戏。
Example
示例:
输入: 4
输出: false
解释: 如果堆中有 4 块石头，那么你永远不会赢得比赛；
因为无论你拿走 1 块、2 块 还是 3 块石头，最后一块石头总是会被你的朋友拿走。
Program
动规
动规的思路，从当前i+1~i+3选，如果能赢就返回，或者后一个选手能输，就能赢。
很遗憾，超时。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<int> vis;
    int N;
    bool dfs(int i){
        if(vis[i]) return vis[i];
        bool isWin=false;
        for(int s=3;s>=1;s--){
            if(i+s>=N) return true;
            else if(!dfs(i+s)) isWin=true;;
        }
        vis[i]=isWin;
        return isWin;
    }
    bool canWinNim(int n) {
        N=n;
        vis.resize(n+1, false);
        return dfs(0);
    }
};

另一个动规，然而n范围太大，内存超了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    bool canWinNim(int n) {
        if(n<=3) return true;
        bool DP[n+1];
        memset(DP, false, sizeof(DP));
        DP[1]=DP[2]=DP[3]=true;
        for(int i=4;i<=n;i++){
            for(int s=1;s<=3;s++){
                if(!DP[i-s]){
                    DP[i]=true;
                    break;
                }
            }
        }
        return DP[n];
    }
};

空间优化还是超时！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    bool canWinNim(int n) {
        if(n<=3) return true;
        // bool DP[n+1];
        // memset(DP, false, sizeof(DP));
        // DP[1]=DP[2]=DP[3]=true;
        bool dp[4];
        dp[1]=dp[2]=dp[3]=true;
        bool nowDP=false;
        for(int i=4;i<=n;i++){
            nowDP=false;
            for(int s=1;s<=3;s++){
                if(!dp[s]){
                    nowDP=true;
                    break;
                }
            }
            dp[1]=dp[2];
            dp[2]=dp[3];
            dp[3]=nowDP;
        }
        return nowDP;
    }
};

博弈论
由于选手足够聪明和规则巧妙设计，先手在给出的状态下总是必胜或者必败的。

必败态和必胜态的定义：
必胜态：如果一个状态的后继状态中存在必败态，那么这种该状态下，先手必胜。
必败态：如果一个状态的所有后继状态都是必胜态，那么这种状态下，先手必败。

（1）无法进行任何移动的局面（也就是terminal position）是必败态；
（2）可以移动到必败态的局面是必胜态；
（3）所有移动都导致必胜态的局面是必败态。
（4）若面临末状态者为获胜则末状态为胜态否则末状态为必败态。
（5）一个局面是胜态的充要条件是该局面进行某种决策后会成为必败态。
（6）一个局面是必败态的充要条件是该局面无论进行何种决策均会成为胜态

这与我们的dfs思路是一致的。
根据以上两个DP的分析，一个必败态（比如4）必能转成三个必胜态（1,2,3）。
而4为必败态，可以推到5,6,7为必胜态；
由必胜态5,6,7，可得8为必败态；
同理，9,10,11,必胜态，12必败态…
所以凡为4的倍数都为必败态，包括0.

1
2
3
4
5
6
class Solution {
public:
    bool canWinNim(int n) {
        return n%(3+1)!=0;
    }
};

1025. 除数博弈

Description
爱丽丝和鲍勃一起玩游戏，他们轮流行动。爱丽丝先手开局。
最初，黑板上有一个数字 N 。在每个玩家的回合，玩家需要执行以下操作：
选出任一 x，满足 $0 < x < N 且 N % x == 0$ 。
用 N - x 替换黑板上的数字 N 。
如果玩家无法执行这些操作，就会输掉游戏。
只有在爱丽丝在游戏中取得胜利时才返回 True，否则返回 false。假设两个玩家都以最佳状态参与游戏。
Example
示例 1：
输入：2
输出：true
解释：爱丽丝选择 1，鲍勃无法进行操作。

示例 2：
输入：3
输出：false
解释：爱丽丝选择 1，鲍勃也选择 1，然后爱丽丝无法进行操作。

提示：
1 <= N <= 1000
Program
记忆化搜索
只要当前选择x后，对手会输，则自己会赢！
超时。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int vis[1001];
    bool dfs(int N){
        if(vis[N]!=-1) return vis[N];
        bool isWin=false;
        for(int x=1;x<N;x++){
            if(N%x==0){
                if(!divisorGame(N-x)){
                    isWin=true;
                    break;
                };
            }
        }
        // cout<<N<<" "<<isWin<<endl;
        vis[N]=isWin;
        return isWin;
    }
    bool divisorGame(int N) {
        memset(vis, -1, sizeof(vis));
        return dfs(N);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    unordered_map<int, bool> m;
    bool dfs(int n){
        if(n==1) return false;//必败
        if(m.find(n)!=m.end()) return m[n];
        bool isWin=false;
        for(int i=1;i<n;i++){
            if(n%i==0) isWin|=!dfs(n-i);
        }
        m[n]=isWin;
        return m[n];
    }
    bool divisorGame(int N) {
        return dfs(N);
    }
};

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    bool divisorGame(int N) {
        bool DP[1001];
        memset(DP, false, sizeof(DP));
        for(int i=1;i<=N;i++){
            for(int x=1;x<i;x++){
                if(i%x==0&&!DP[i-x]){
                    DP[i]=true;
                    break;
                }
            }
            //cout<<DP[i]<<endl;
        }
        return DP[N];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    bool divisorGame(int N) {
        bool DP[N+1];
        memset(DP, false, sizeof(DP));
        for(int i=2;i<=N;i++){
            for(int j=1;j<i;j++){
                if(i%j==0) DP[i]|=!DP[i-j];
            }
        }
        return DP[N];
    }
};

博弈论
由于选手足够聪明和规则巧妙设计，先手在给出的状态下总是必胜或者必败的。

必败态和必胜态的定义：
必胜态：如果一个状态的后继状态中存在必败态，那么这种该状态下，先手必胜。
必败态：如果一个状态的所有后继状态都是必胜态，那么这种状态下，先手必败。

（1）无法进行任何移动的局面（也就是terminal position）是必败态；
（2）可以移动到必败态的局面是必胜态；
（3）所有移动都导致必胜态的局面是必败态。
（4）若面临末状态者为获胜则末状态为胜态否则末状态为必败态。
（5）一个局面是胜态的充要条件是该局面进行某种决策后会成为必败态。
（6）一个局面是必败态的充要条件是该局面无论进行何种决策均会成为胜态
image
与上文dfs和动规思路一致，这里设P为必胜态，N为必败态，那么一个状态能够转到另一个必败态则该状态为必胜态！
如图所示：
1：可见无法操作，必败态！
2：只有一种操作，到1，所以必胜态！
3：只有一种操作，到2，必败态！
4：两种操作，到3和2，可以到达必败态，所以此为必胜态！
…
可以看出规律，偶数必胜，奇数必败！

1
2
3
4
5
6
class Solution {
public:
    bool divisorGame(int N) {
        return N%2==0;
    }
};

877. 石子游戏

Description
亚历克斯和李用几堆石子在做游戏。偶数堆石子排成一行，每堆都有正整数颗石子 piles[i] 。
游戏以谁手中的石子最多来决出胜负。石子的总数是奇数，所以没有平局。
亚历克斯和李轮流进行，亚历克斯先开始。 每回合，玩家从行的开始或结束处取走整堆石头。 这种情况一直持续到没有更多的石子堆为止，此时手中石子最多的玩家获胜。
假设亚历克斯和李都发挥出最佳水平，当亚历克斯赢得比赛时返回 true ，当李赢得比赛时返回 false 。
Example
示例：
输入：[5,3,4,5]
输出：true
解释：
亚历克斯先开始，只能拿前 5 颗或后 5 颗石子 。
假设他取了前 5 颗，这一行就变成了 [3,4,5] 。
如果李拿走前 3 颗，那么剩下的是 [4,5]，亚历克斯拿走后 5 颗赢得 10 分。
如果李拿走后 5 颗，那么剩下的是 [3,4]，亚历克斯拿走后 4 颗赢得 9 分。
这表明，取前 5 颗石子对亚历克斯来说是一个胜利的举动，所以我们返回 true 。

提示：
2 <= piles.length <= 500
piles.length 是偶数。
1 <= piles[i] <= 500
sum(piles) 是奇数。
Program
记忆化搜索
记dfs(sum, i, j)为当前区间[i,j]，和为sum时，选手最优得分，
很明显：
(1)$i>j$时，return 0;

(2)计算区间[i,j]时，选手的最优得分

  • 选择头元素，score1=piles[i]+sum-piles[i]-dfs(sum-piles[i], i+1, j); //此时dfs为另一个选手的最优得分，本选手最优得分当然是区间[i+1,j]和减去下个选手在[i+1,j]上的最优得分，以下同理。
  • 选择尾元素，score2=piles[j]+sum-piles[j]-dfs(sum-piles[j], i,j-1);
    所以当前选手最优得分：score=max(score1, score2);

(3)有重复计算，记录vis[i][j]即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<vector<int>> vis;
    int dfs(vector<int>& piles,int sum, int i, int j){
        if(i>j) return 0;
        if(vis[i][j]!=-1) return vis[i][j];
        int ans=0;
        int score1=piles[i]+sum-piles[i]-dfs(piles, sum-piles[i], i+1,j);
        int score2=piles[j]+sum-piles[j]-dfs(piles, sum-piles[j], i, j-1);
        ans=max(score1, score2);
        vis[i][j]=ans;
        return ans;
    }
    bool stoneGame(vector<int>& piles) {
        int n=piles.size();
        int sum=0;
        vis.resize(n, vector<int>(n, -1));
        for(int x:piles) sum+=x;
        return dfs(piles, sum, 0, n-1)>sum/2;
    }
};

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    bool stoneGame(vector<int>& piles) {
        int n=piles.size();
        vector<int> sum(n, 0);  //前缀和
        for(int i=0;i<n;i++){
            sum[i]+=piles[i];
            if(i>0) sum[i]+=sum[i-1];
        }
        vector<vector<int>> DP(n, vector<int>(n, 0));
        for(int i=n-1;i>=0;i--){
            for(int j=i;j<n;j++){
                int s=(i>0)?sum[j]-sum[i-1]:sum[j];
                if(i+1<n) DP[i][j]=max(DP[i][j], piles[i]+s-piles[i]-DP[i+1][j]);
                if(j-1>=0)DP[i][j]=max(DP[i][j], piles[j]+s-piles[j]-DP[i][j-1]);
            }
        }
        return DP[0][n-1]>sum[n-1]/2;
    }
};

dfs/记忆化搜索

638. 大礼包

Description
在LeetCode商店中， 有许多在售的物品。
然而，也有一些大礼包，每个大礼包以优惠的价格捆绑销售一组物品。
现给定每个物品的价格，每个大礼包包含物品的清单，以及待购物品清单。请输出确切完成待购清单的最低花费。
每个大礼包的由一个数组中的一组数据描述，最后一个数字代表大礼包的价格，其他数字分别表示内含的其他种类物品的数量。
任意大礼包可无限次购买。
Example
示例 1:
输入: [2,5], [[3,0,5],[1,2,10]], [3,2]
输出: 14
解释:
有A和B两种物品，价格分别为¥2和¥5。
大礼包1，你可以以¥5的价格购买3A和0B。
大礼包2， 你可以以¥10的价格购买1A和2B。
你需要购买3个A和2个B， 所以你付了¥10购买了1A和2B（大礼包2），以及¥4购买2A。

示例 2:
输入: [2,3,4], [[1,1,0,4],[2,2,1,9]], [1,2,1]
输出: 11
解释:
A，B，C的价格分别为¥2，¥3，¥4.
你可以用¥4购买1A和1B，也可以用¥9购买2A，2B和1C。
你需要买1A，2B和1C，所以你付了¥4买了1A和1B（大礼包1），以及¥3购买1B， ¥4购买1C。
你不可以购买超出待购清单的物品，尽管购买大礼包2更加便宜。

说明:
最多6种物品， 100种大礼包。
每种物品，你最多只需要购买6个。
你不可以购买超出待购清单的物品，即使更便宜。
Program
①暴力
这题不好DP，相反深搜更容易些，因为物品种类会变化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    int minSum=0x3f3f3f3f;
    void DFS(vector<int>& price, vector<vector<int>>& special, vector<int> needs, int sum){
        if(sum>minSum) return;  //剪枝
        for(int i=0;i<special.size();i++){
            int n=special[i].size();
            vector<int> tmpNeeds(needs.begin(), needs.end());
            bool isPass=true;
            for(int j=0;j<n-1;j++){
                if(special[i][j]>needs[j]){
                    isPass=false;
                    break;
                }
                else tmpNeeds[j]-=special[i][j];
            }
            if(isPass) DFS(price, special, tmpNeeds, sum+special[i][n-1]);
        }
        for(int i=0;i<needs.size();i++){
            sum+=needs[i]*price[i];
        }
        minSum=min(minSum, sum);
    }
    int shoppingOffers(vector<int>& price, vector<vector<int>>& special,
    vector<int>& needs) {
        DFS(price, special, needs, 0);
        return minSum;
    }
};

②记忆化搜索
注意到needs可能会重复计算！所以可以记忆化搜索！然而，好像和暴力的做法速度差不多，leetcode判题的时间结果有浮动啊。。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    int minSum=0x3f3f3f3f;
    unordered_map<int, int> vis;
    int cal(vector<int>& needs){
        int ans=0;
        for(int x:needs){
            ans=ans*10+x;
        }
        return ans;
    }
    void DFS(vector<int>& price, vector<vector<int>>& special, vector<int> needs, int sum){
        if(sum>minSum) return;  //剪枝
        if(vis.find(cal(needs))!=vis.end()) return; //已记录
        for(int i=0;i<special.size();i++){
            int n=special[i].size();
            vector<int> tmpNeeds(needs.begin(), needs.end());
            bool isPass=true;
            for(int j=0;j<n-1;j++){
                if(special[i][j]>needs[j]){
                    isPass=false;
                    break;
                }
                else tmpNeeds[j]-=special[i][j];
            }
            if(isPass) DFS(price, special, tmpNeeds, sum+special[i][n-1]);
        }
        for(int i=0;i<needs.size();i++){
            sum+=needs[i]*price[i];
        }
        minSum=min(minSum, sum);
        vis[cal(needs)] = minSum;
    }
    int shoppingOffers(vector<int>& price, vector<vector<int>>& special,
    vector<int>& needs) {
        DFS(price, special, needs, 0);
        return minSum;
    }
};

650. 只有两个键的键盘

Description
最初在一个记事本上只有一个字符 ‘A’。你每次可以对这个记事本进行两种操作：
Copy All (复制全部) : 你可以复制这个记事本中的所有字符(部分的复制是不允许的)。
Paste (粘贴) : 你可以粘贴你上一次复制的字符。
给定一个数字 n 。你需要使用最少的操作次数，在记事本中打印出恰好 n 个 ‘A’。输出能够打印出 n 个 ‘A’ 的最少操作次数。
Example
示例 1:
输入: 3
输出: 3
解释:
最初, 我们只有一个字符 ‘A’。
第 1 步, 我们使用 Copy All 操作。
第 2 步, 我们使用 Paste 操作来获得 ‘AA’。
第 3 步, 我们使用 Paste 操作来获得 ‘AAA’。
说明:
n 的取值范围是 [1, 1000] 。
Program
①暴力

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    const int inf=0x3f3f3f3f;
    int minStep=inf;
    void helper(int n,int cur, int step, int c, bool isCopy){
        if(step>minStep) return;
        if(cur>n) return;
        if(cur==n){
            minStep=min(minStep, step);
            return;
        }
        if(!isCopy)helper(n, cur, step+1, cur, true); //isCopy防止重复copy
        if(c!=0) helper(n, cur+c, step+1, c, false);    
    }
    int minSteps(int n) {
        helper(n, 1, 0, 0, false);
        return minStep;
    }
};

②分解质因数
将所有操作分成以 copy 为首的多组，形如 (copy, paste, …, paste)，再使用 C 代表 copy，P 代表 paste。例如操作 CPPCPPPPCP 可以分为 [CPP][CPPPP][CP] 三组。
假设每组的长度为 g_1, g_2, …。完成第一组操作后，字符串有 g_1 个 A，完成第二组操作后字符串有 g_1 * g_2 个 A。当完成所有操作时，共有 g_1 * g_2 * … * g_n 个 ‘A’。
我们最终想要 N = g_1 * g_2 * … * g_n 个 A。如果 g_i 是合数，存在 g_i = p * q，那么这组操作可以分解为两组，第一组包含 1 个 C 和 p-1 个 P，第二组包含 1 个 C 和 q-1 个 P。
现在证明这种分割方式使用的操作最少。原本需要 pq 步操作，分解后需要 p+q 步。因为 p+q <= pq，等价于 1 <= (p-1)(q-1)，当 p >= 2 且 q >= 2 时上式永远成立。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    unordered_map<int, int> m;
    int minSteps(int n) {
        if(n==1) return 0;
        for(int i=2;i*i<=n;i++){
            if(n%i==0){
                if(m.find(i)==m.end()) m[i]=minSteps(i);
                if(m.find(n/i)==m.end()) m[n/i]=minSteps(n/i);
                return m[i]+m[n/i];
            }
        }
        if(m.find(n)==m.end()) m[n]=n;
        return m[n];
    }
};

因式分解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int minSteps(int n) {
        int ans = 0, prime = 2;
        while(n > 1){
            while(n % prime == 0){
                ans += prime;
                n /= prime;
            }
            prime ++ ;
        }
        return ans;
    }
};

动态规划
设dp[i]为i个A的最小操作数，状态转移方程：
dp[i] = min(dp[j] + i / j), i %j ==0 —— i个A可以由j个A copy一次以及paste i / j - 1次
初始化
dp[1] = 0
dp[i] = i

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int minSteps(int n) {
        int dp[n + 1];
        memset(dp, 0, sizeof(dp));
        for(int i = 2; i <= n; i ++){
            dp[i] = i; //初始化
            for(int j = 2; j < i; j ++){
                if(i % j == 0) dp[i] = min(dp[i], dp[j] + i / j);
            }
        }
        return dp[n];
    }
};

698. 划分为k个相等的子集

Description
给定一个整数数组 nums 和一个正整数 k，找出是否有可能把这个数组分成 k 个非空子集，其总和都相等。
Example
示例 1：
输入： nums = [4, 3, 2, 3, 5, 2, 1], k = 4
输出： True
说明： 有可能将其分成 4 个子集（5），（1,4），（2,3），（2,3）等于总和。
注意:

1
2
1 <= k <= len(nums) <= 16
0 < nums[i] < 10000

Program
①暴力枚举集合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    vector<int> h;
    int n;
    bool dfs(int u, int p){
        if(u==h.size()) return p == (1<<n)-1;    //关键，少于k也能判断
        return dfs(u+1,p) || (!(h[u]&p) && dfs(u+1,p|h[u]));
    }
    bool canPartitionKSubsets(vector<int>& nums, int k) {
        n = nums.size();
        int target = 0;
        for(int x:nums) target += x;
        if(target % k) return false;
        target /= k;

        for(int i = 0 ; i < 1<<n ; i++) {
            int s = 0;
            for(int j = 0 ; j < n ; j++)
                if(i>>j&1)
                    s += nums[j];
            if(s==target) h.push_back(i);
        }
        return dfs(0,0);
    }
};

DFS
分成k个集合，依次枚举，然鹅还是的优化，对nums降序排列！较大的数更容易确定位置！减少递归次数！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<int> h;
    int n;
    int target=0;
    vector<int> path;
    bool dfs(vector<int>& nums, int u){
        if(u==n){
            for(int x:path) if(x!=target) return false;
            return true;
        }
        if(nums[u]>target) return false;
        for(int i=0;i<path.size();i++){
            if(nums[u]+path[i]>target)continue;
            path[i]+=nums[u];
            if(dfs(nums, u+1)) return true;
            path[i]-=nums[u];
        }
        return false;
    }
    bool canPartitionKSubsets(vector<int>& nums, int k) {
        n=nums.size();
        for(int x:nums) target+=x;
        if((target%k)) return false;
        path.resize(k ,0);
        target/=k;
        sort(nums.begin(), nums.end(), greater<int>());  //优化
        return dfs(nums,0);
    }
};

983. 最低票价

Description
在一个火车旅行很受欢迎的国度，你提前一年计划了一些火车旅行。在接下来的一年里，你要旅行的日子将以一个名为 days 的数组给出。每一项是一个从 1 到 365 的整数。
火车票有三种不同的销售方式：

  • 一张为期一天的通行证售价为 costs[0] 美元；
  • 一张为期七天的通行证售价为 costs[1] 美元；
  • 一张为期三十天的通行证售价为 costs[2] 美元。
    通行证允许数天无限制的旅行。 例如，如果我们在第 2 天获得一张为期 7 天的通行证，那么我们可以连着旅行 7 天：第 2 天、第 3 天、第 4 天、第 5 天、第 6 天、第 7 天和第 8 天。
    返回你想要完成在给定的列表 days 中列出的每一天的旅行所需要的最低消费。

Example
示例 1：
输入：days = [1,4,6,7,8,20], costs = [2,7,15]
输出：11
解释：
例如，这里有一种购买通行证的方法，可以让你完成你的旅行计划：
在第 1 天，你花了 costs[0] = 2 买了一张为期 1 天的通行证，它将在第 1 天生效。
在第 3 天，你花了 costs[1] = 7 买了一张为期 7 天的通行证，它将在第 3, 4, …, 9 天生效。
在第 20 天，你花了 costs[0] = 2 买了一张为期 1 天的通行证，它将在第 20 天生效。
你总共花了 11，并完成了你计划的每一天旅行。

示例 2：
输入：days = [1,2,3,4,5,6,7,8,9,10,30,31], costs = [2,7,15]
输出：17
解释：
例如，这里有一种购买通行证的方法，可以让你完成你的旅行计划：
在第 1 天，你花了 costs[2] = 15 买了一张为期 30 天的通行证，它将在第 1, 2, …, 30 天生效。
在第 31 天，你花了 costs[0] = 2 买了一张为期 1 天的通行证，它将在第 31 天生效。
你总共花了 17，并完成了你计划的每一天旅行。

提示：
1 <= days.length <= 365
1 <= days[i] <= 365
days 按顺序严格递增
costs.length == 3
1 <= costs[i] <= 1000
Program
记忆化搜索
首先定义dfs(i, resDay)为当前第days[i]天，通行证有效期的截止时间为resDay的最低消费。
设n为days长度
①i>n，return 0；超出days的日期长度了
②days[i]<=resDay，当前第days[i]天在前一次通行证有效期内，计算下一天dfs(i+1,resDay)即可
③days[i]>resDay，
那么当前第days[i]天可以买三种票价
ans=min(ans, costs[j]+dfs(i+1,days[j]+cosDays[j]-1)), j=0,1,2即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    const int cosDays[3]={1,7,30};
    int n;
    map<pair<int,int>, int> m;
    int dfs(vector<int>& days, vector<int>& costs,int i, int resDay){
        if(i>=n) return 0;
        if(m.find(pair<int,int>(i, resDay))!=m.end()) return m[pair<int,int>(i, resDay)];
        if(days[i]<=resDay) return dfs(days, costs, i+1, resDay);
        int ans=INT_MAX;
        for(int j=0;j<3;j++){
            ans=min(ans, costs[j]+dfs(days, costs, i+1, days[i]+cosDays[j]-1));
        }
        m[pair<int,int>(i, resDay)] = ans;
        return ans;
    }
    int mincostTickets(vector<int>& days, vector<int>& costs) {
        n=days.size();
        return dfs(days, costs, 0, 0);
    }
};

resDay表示剩余天数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    const int cosDays[3]={1,7,30};
    int n;
    vector<vector<int>> vis;
    int dfs(vector<int>& days, vector<int>& costs, int i, int resDay){
        if(i>=n) return 0;
        if(vis[i][resDay]!=-1) return vis[i][resDay];
        if(i>0){
            int rd=resDay-(days[i]-days[i-1]);
            if(rd>=0) return dfs(days, costs, i+1, rd);
        }
        int ans=INT_MAX;
        for(int j=0;j<3;j++){
            ans=min(ans, costs[j]+dfs(days, costs, i+1, cosDays[j]-1));
        }
        vis[i][resDay]=ans;
        return ans;
    }
    int mincostTickets(vector<int>& days, vector<int>& costs) {
        n=days.size();
        vis.resize(n,vector<int>(31,-1));
        return dfs(days, costs, 0, 0);
    }
};

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    const int cosDays[3]={1,7,30};
    int n;
    const int inf=0x3f3f3f3f;
    int mincostTickets(vector<int>& days, vector<int>& costs) {
        n=days.size();
        int DP[n][396];
        memset(DP, inf, sizeof(DP));
        for(int i=n-1;i>=0;i--){
            for(int d=0;d<=395;d++){
                if(d>=days[i]){
                    if(i<n-1) DP[i][d]=DP[i+1][d];
                    else DP[i][d]=0;
                    continue;
                }
                for(int j=0;j<3;j++){
                    if(i<n-1)DP[i][d]=min(DP[i][d], costs[j]+DP[i+1][days[i]+cosDays[j]-1]);
                    else DP[i][d]=min(DP[i][d], costs[j]);
                }
            }
        }
        return DP[0][0];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    const int cosDays[3]={1,7,30};
    int n;
    const int inf=0x3f3f3f3f;
    int mincostTickets(vector<int>& days, vector<int>& costs) {
        n=days.size();
        int DP[n][31];
        memset(DP, inf, sizeof(DP));
        for(int i=n-1;i>=0;i--){
            for(int d=0;d<=30;d++){
                if(i>0){
                    int rd=d-(days[i]-days[i-1]);
                    if(rd>=0){
                        if(i+1<n)DP[i][d]=DP[i+1][rd];
                        else DP[i][d]=0;
                        continue;
                    }
                }
                for(int j=0;j<3;j++){
                    if(i<n-1)DP[i][d]=min(DP[i][d], costs[j]+DP[i+1][cosDays[j]-1]);
                    else DP[i][d]=min(DP[i][d], costs[j]);
                }
            }
        }
        return DP[0][0];
    }
};

一维DP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    int mincostTickets(vector<int>& days, vector<int>& costs) {
        int last = days[days.size()-1];

        vector<int> dp(last+1, 0);
        int idx = 0;

        for (int i = 1; i <= last; i++) {
            if (i == days[idx]) {
                int cost = INT_MAX;
                int oneDayAgo = i-1;
                int sevenDaysAgo = i-7>0?i-7:0;
                int thirtyDaysAgo = i-30>0?i-30:0;

                cost = min(dp[oneDayAgo] + costs[0], cost);
                cost = min(dp[sevenDaysAgo] + costs[1], cost);
                cost = min(dp[thirtyDaysAgo] + costs[2], cost);

                dp[i] = cost;

                idx++;
            } else {
                dp[i] = dp[i-1];
            }
        }

        return dp[last];
    }
};

1339. 分裂二叉树的最大乘积

Description
给你一棵二叉树，它的根为 root 。请你删除 1 条边，使二叉树分裂成两棵子树，且它们子树和的乘积尽可能大。
由于答案可能会很大，请你将结果对 10^9 + 7 取模后再返回。
Example
示例 1：

输入：root = [1,2,3,4,5,6]
输出：110
解释：删除红色的边，得到 2 棵子树，和分别为 11 和 10 。它们的乘积是 110 （11*10）

示例 2：
输入：root = [1,null,2,3,4,null,null,5,6]
输出：90
解释：移除红色的边，得到 2 棵子树，和分别是 15 和 6 。它们的乘积为 90 （15*6）

示例 3：
输入：root = [2,3,9,10,7,8,6,5,4,11,1]
输出：1025

示例 4：
输入：root = [1,1]
输出：1

提示：
每棵树最多有 50000 个节点，且至少有 2 个节点。
每个节点的值在 [1, 10000] 之间。
Program
思路
二叉树总和为totalSum,子树和为sum，则最终答案取$(totalSum-sum) * sum$最大的即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    const int MOD=1e9+7;
    unordered_map<TreeNode*, long long> m;
    long long calSum(TreeNode* root){
        if(root==NULL) return 0;
        long long sum=root->val;
        sum+=calSum(root->left);
        sum+=calSum(root->right);
        m[root]=sum;
        return sum;
    }
    int maxProduct(TreeNode* root) {
        long long totalSum=calSum(root);
        queue<TreeNode*> q;
        q.push(root);
        long long ans=0;
        while(!q.empty()){
            TreeNode* node=q.front();q.pop();
            if(node->left!=NULL){
                long long sum=m[node->left];
                long long x=sum*(totalSum-sum);
                ans=ans>x?ans:x;
                q.push(node->left);
            }
            if(node->right!=NULL){
                long long sum=m[node->right];
                long long x=sum*(totalSum-sum);
                ans=ans>x?ans:x;
                q.push(node->right);
            }
        }
        return ans%MOD;
    }
};

计算子树和最接近totalSum的一半

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    const int MOD=1e9+7;
    int ans=0;
    int totalSum=0;
    void calSum(TreeNode* root){
        if(root==NULL) return;
        totalSum+=root->val;
        calSum(root->left);
        calSum(root->right);
    }
    int calBest(TreeNode* root){
        if(root==NULL) return 0;
        int sum=root->val+calBest(root->left)+calBest(root->right);
        if(abs(sum*2-totalSum)<abs(ans*2-totalSum)) ans=sum; //记录最接近totalSum一半的数！
        return sum;
    }
    int maxProduct(TreeNode* root) {
        calSum(root);
        calBest(root);
        return (long long)ans*(totalSum-ans)%MOD;
    }
};

1367. 二叉树中的列表

Description
给你一棵以 root 为根的二叉树和一个 head 为第一个节点的链表。
如果在二叉树中，存在一条一直向下的路径，且每个点的数值恰好一一对应以 head 为首的链表中每个节点的值，那么请你返回 True ，否则返回 False 。
一直向下的路径的意思是：从树中某个节点开始，一直连续向下的路径。
Example
示例 1：
image
输入：head = [4,2,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
输出：true
解释：树中蓝色的节点构成了与链表对应的子路径。

示例 2：
image
输入：head = [1,4,2,6], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
输出：true

示例 3：
输入：head = [1,4,2,6,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
输出：false
解释：二叉树中不存在一一对应链表的路径。

提示：
二叉树和链表中的每个节点的值都满足 1 <= node.val <= 100 。
链表包含的节点数目在 1 到 100 之间。
二叉树包含的节点数目在 1 到 2500 之间。
Program
枚举二叉树每个节点进行链表头结点进行匹配。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool dfs(TreeNode* root, ListNode* head){
        if(head==NULL) return true; //完成匹配
        if(root==NULL) return false; //匹配不完全
        if(root->val!=head->val) return false; //匹配不成功
        return dfs(root->left, head->next) || dfs(root->right, head->next); //匹配孩子
    }
    bool isSubPath(ListNode* head, TreeNode* root) {
        if(root==NULL) return false;
        return dfs(root, head) || isSubPath(head, root->left) || isSubPath(head, root->right); //枚举每个节点当成链表头结点
    }
};

967. 连续差相同的数字

Description
返回所有长度为 N 且满足其每两个连续位上的数字之间的差的绝对值为 K 的非负整数。
请注意，除了数字 0 本身之外，答案中的每个数字都不能有前导零。例如，01 因为有一个前导零，所以是无效的；但 0 是有效的。
你可以按任何顺序返回答案。
Example
示例 1：
输入：N = 3, K = 7
输出：[181,292,707,818,929]
解释：注意，070 不是一个有效的数字，因为它有前导零。

示例 2：
输入：N = 2, K = 1
输出：[10,12,21,23,32,34,43,45,54,56,65,67,76,78,87,89,98]

提示：
1 <= N <= 9
0 <= K <= 9
Program
暴力dfs
最差时间复杂度：$O(9 * 2^8)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<int> res;
    void dfs(int i, int num, int bit, int n, int k){
        if(i==n){
            res.push_back(num);
            return;
        }
        if(k!=0&&bit-k>=0) dfs(i+1, num*10+bit-k, bit-k, n, k);
        if(k!=0&&bit+k<=9) dfs(i+1, num*10+bit+k, bit+k, n, k);
        if(k==0) dfs(i+1, num*10+bit, bit, n, k);
    }
    vector<int> numsSameConsecDiff(int N, int K) {
        for(int i=0;i<=9;i++){
            if(i==0&&N!=1) continue; //1,0特例
            dfs(1, i, i, N, K);
        }
        return res;
    }
};

概率DP

688. “马”在棋盘上的概率

Description
已知一个 NxN 的国际象棋棋盘，棋盘的行号和列号都是从 0 开始。即最左上角的格子记为 (0, 0)，最右下角的记为 (N-1, N-1)。
现有一个 “马”（也译作 “骑士”）位于 (r, c) ，并打算进行 K 次移动。
如下图所示，国际象棋的 “马” 每一步先沿水平或垂直方向移动 2 个格子，然后向与之相垂直的方向再移动 1 个格子，共有 8 个可选的位置。
image
现在 “马” 每一步都从可选的位置（包括棋盘外部的）中独立随机地选择一个进行移动，直到移动了 K 次或跳到了棋盘外面。
求移动结束后，“马” 仍留在棋盘上的概率。
Example
示例：
输入: 3, 2, 0, 0
输出: 0.0625
解释:
输入的数据依次为 N, K, r, c
第 1 步时，有且只有 2 种走法令 “马” 可以留在棋盘上（跳到（1,2）或（2,1））。对于以上的两种情况，各自在第2步均有且只有2种走法令 “马” 仍然留在棋盘上。
所以 “马” 在结束后仍在棋盘上的概率为 0.0625。

注意：
N 的取值范围为 [1, 25]
K 的取值范围为 [0, 100]
开始时，“马” 总是位于棋盘上
Program
设DP[k][i][j]为在位置(i, j)时已走过k步的概率，注意如果表示可能走的路径数则会超数值范围。
那么$DP[k][i][j]=\frac{\sum{DP[k-1][x][y]}}{8}$其中x,y为可走的位置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
public:
    int step[8][2]={
        -2, 1,
        -1, 2,
        1, 2,
        2, 1,
        2, -1,
        1, -2,
        -1, -2,
        -2, -1
    };

    bool judge(int N, int x, int y){
        if(x<0||x>=N||y<0||y>=N) return false;
        return true;
    }
    double knightProbability(int N, int K, int r, int c) {
        vector<vector<vector<double>>> DP(K+1, vector<vector<double>>(N, vector<double>(N, 0)));
        for(int k=0;k<=K;k++){
            for(int i=0;i<N;i++){
                for(int j=0;j<N;j++){
                    if(k==0){
                        DP[k][i][j]=1;
                        continue;
                    }
                    for(int s=0;s<8;s++){
                        int x=i+step[s][0];
                        int y=j+step[s][1];
                        if(judge(N, x, y)){
                            DP[k][i][j]+=DP[k-1][x][y];    
                        }
                    }
                    DP[k][i][j]/=8;
                }
            }
        }
        return DP[K][r][c];
    }
};

808. 分汤

Description
有 A 和 B 两种类型的汤。一开始每种类型的汤有 N 毫升。有四种分配操作：
提供 100ml 的汤A 和 0ml 的汤B。
提供 75ml 的汤A 和 25ml 的汤B。
提供 50ml 的汤A 和 50ml 的汤B。
提供 25ml 的汤A 和 75ml 的汤B。
当我们把汤分配给某人之后，汤就没有了。每个回合，我们将从四种概率同为0.25的操作中进行分配选择。如果汤的剩余量不足以完成某次操作，我们将尽可能分配。当两种类型的汤都分配完时，停止操作。
注意不存在先分配100 ml汤B的操作。
需要返回的值： 汤A先分配完的概率 + 汤A和汤B同时分配完的概率 / 2。
Example
示例:
输入: N = 50
输出: 0.625
解释:
如果我们选择前两个操作，A将首先变为空。对于第三个操作，A和B会同时变为空。对于第四个操作，B将首先变为空。
所以A变为空的总概率加上A和B同时变为空的概率的一半是 $0.25 (1 + 1 + 0.5 + 0)= 0.625$。
注释:
0 <= N <= 10^9。
返回值在 10^-6 的范围将被认为是正确的。
*Program**
DP
$DP[i][j]=\sum{DP[i-x[k]][j-y[k]]}$，注意边界，超内存！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    const int step[4][2]={
        100, 0,
        75, 25,
        50, 50,
        25, 75
    };
    double soupServings(int N) {
        vector<vector<double>> DP(N+1, vector<double>(N+1, 0));
        for(int i=0;i<=N;i++){
            for(int j=0;j<=N;j++){
                if(i==0&&j==0){
                    DP[i][j]=0.5;
                    continue;
                }else if(i==0){
                    DP[i][j]=1;
                    continue;
                }else if(j==0){
                    DP[i][j]=0;
                    continue;
                }
                for(int k=0;k<4;k++){
                    int x=i-step[k][0];
                    int y=j-step[k][1];
                    if(x<=0&&y<=0) DP[i][j]+=0.25*DP[0][0];
                    else if(x<=0) DP[i][j]+=0.25*DP[0][y];
                    else if(y<=0) DP[i][j]+=0.25*DP[x][0];
                    else DP[i][j]+=0.25*DP[x][y];
                }
            }
        }
        return DP[N][N];
    }
};

优化
四种操作都是25的倍数，所以可以N/25(有余数，加1)来减少内存。即使将 N 除以 25 之后，仍然没法在短时间内得到答案，因此我们需要尝试一些别的思路。可以发现，分配操作有 (4, 0)，(3, 1)，(2, 2) 和 (1, 3) 四种，那么在一次分配中，汤 A 平均会少 (4 + 3 + 2 + 1) / 4 = 2.5 份，汤 B 平均会少 (0 + 1 + 2 + 3) / 4 = 1.5 份。因此在 N 非常大的时候，A 会有很大的概率比 B 先分配完，所有概率应该非常接近 1。事实上，当 N >= 500 * 25 时，所求概率已经大于 0.999999 了（可以通过上面的动态规划方法求出），它和 1 的误差（无论是绝对误差还是相对误差）都小于 10^-6。因此在 N >= 500 * 25 时，我们只需要输出 1 作为答案即可。在其它的情况下，我们使用动态规划计算出答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
public:
    const int step[4][2]={
        100/25, 0/25,
        75/25, 25/25,
        50/25, 50/25,
        25/25, 75/25
    };
    double soupServings(int N) {
        N=N/25+((N%25)?1:0);
        if(N>=500) return 0.999999;
        double DP[N+1][N+1];
        memset(DP, 0.0, sizeof(DP));
        for(int i=0;i<=N;i++){
            for(int j=0;j<=N;j++){
                if(i==0&&j==0){
                    DP[i][j]=0.5;
                    continue;
                }else if(i==0){
                    DP[i][j]=1;
                    continue;
                }else if(j==0){
                    DP[i][j]=0;
                    continue;
                }
                for(int k=0;k<4;k++){
                    int x=i-step[k][0];
                    int y=j-step[k][1];
                    if(x<=0&&y<=0) DP[i][j]+=0.25*DP[0][0];
                    else if(x<=0) DP[i][j]+=0.25*DP[0][y];
                    else if(y<=0) DP[i][j]+=0.25*DP[x][0];
                    else DP[i][j]+=0.25*DP[x][y];
                }
            }
        }
        return DP[N][N];
    }
};

837. 新21点

Description
爱丽丝参与一个大致基于纸牌游戏 “21点” 规则的游戏，描述如下：
爱丽丝以 0 分开始，并在她的得分少于 K 分时抽取数字。 抽取时，她从 [1, W] 的范围中随机获得一个整数作为分数进行累计，其中 W 是整数。 每次抽取都是独立的，其结果具有相同的概率。
当爱丽丝获得不少于 K 分时，她就停止抽取数字。 爱丽丝的分数不超过 N 的概率是多少？
Example
示例 1：
输入：N = 10, K = 1, W = 10
输出：1.00000
说明：爱丽丝得到一张卡，然后停止。

示例 2：
输入：N = 6, K = 1, W = 10
输出：0.60000
说明：爱丽丝得到一张卡，然后停止。
在 W = 10 的 6 种可能下，她的得分不超过 N = 6 分。

示例 3：
输入：N = 21, K = 17, W = 10
输出：0.73278

提示：
0 <= K <= N <= 10000
1 <= W <= 10000
如果答案与正确答案的误差不超过 10^-5，则该答案将被视为正确答案通过。
此问题的判断限制时间已经减少。
Program
思路
设DP[i]得分为i开始到最后得分在$[K,N]$内的概率：
（1）$i\in [K,N]$，明显概率就是1；
（2）$i>N$，概率为0；
（3）$0<=i<K$，$DP[i]=\frac{1}{W}\sum^{W}_{j=1}(DP[i+j])$.
但是这里求和的话需要重循环，时间复杂度：$O(n^2)$超时！
优化：后面求和可以通过后缀和求得：
$DP[i]=\frac{1}{W}(lastSum[i+1]-lastSum[i+W+1]))$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    double new21Game(int N, int K, int W) {
        int n=K-1+W;
        double DP[n+1];
        double lastSum[n+1];
        memset(DP, 0, sizeof(DP));
        memset(lastSum, 0, sizeof(lastSum));
        for(int i=n;i>=0;i--){
            if(K<=i&&i<=min(N,n)) DP[i]=1;
            else if(i>N) DP[i]=0;
            else{
                // for(int j=1;j<=W;j++){
                //     DP[i]+=DP[i+j]/W;
                // }
                if(i+W+1<=n) DP[i]+=(lastSum[i+1]-lastSum[i+W+1])/W;
                else DP[i]+=lastSum[i+1]/W;
            }
            lastSum[i]+=DP[i];
            if(i+1<=n) lastSum[i]+=lastSum[i+1];
        }
        return DP[0];
    }
};

1227. 飞机座位分配概率

Description
有 n 位乘客即将登机，飞机正好有 n 个座位。第一位乘客的票丢了，他随便选了一个座位坐下。
剩下的乘客将会：
如果他们自己的座位还空着，就坐到自己的座位上，
当他们自己的座位被占用时，随机选择其他座位
第 n 位乘客坐在自己的座位上的概率是多少？
Example
示例 1：
输入：n = 1
输出：1.00000
解释：第一个人只会坐在自己的位置上。

示例 2：
输入: n = 2
输出: 0.50000
解释：在第一个人选好座位坐下后，第二个人坐在自己的座位上的概率是 0.5。

提示：
1 <= n <= 10^5
Program
动态规划
不妨设$1 ~ n$乘客自己的座位分别为$1 ~ n$,考虑结果DP[n]，第一个乘客选择：
（1）选择1，那么后面每个人都能做到自己的位置，结果$\frac{1}{n}$;
（2）选择n，那么$\frac{1}{n} * 0=0$；
（3）选择$k\in [2,n-1]$，那么$[2,k-1]$的所有人归位正确，第k个乘客进入子问题：

  • 选择乘客1的原位置，则所有人皆大欢喜——与第一个乘客的(1)一样，即此时应当将1座位乘客原本位置作为第k个乘客的原位置！——结果为$\frac{1}{n} * \frac{1}{n-k+1}$；
  • 选择其他位置，同（3）；
    即第k个乘客的选择可以看成DP[n-k+1]。
    故递推公式：$DP[n]=\frac{1}{n}+\frac{1}{n} * \sum^{n-1}{2} * DP[n-k+1]=\frac{1}{n} * (1 + \sum^{n-1}{2} * DP[n-k+1])$。
    时间复杂度：$O(n^2)$，很遗憾n的范围限制超时。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    class Solution {
    public:
        double nthPersonGetsNthSeat(int n) {
            vector<double> DP(n+1, 0);
            for(int i=1;i<=n;i++){
                DP[i]=1/(double)i;
                for(int j=2;j<i-1;j++){
                    DP[i]+=1/(double)i * DP[i-j+1];
                }
            }
            return DP[n];
        }
    };

优化
看到递推公式后一项，可以通过前缀和化简为:$DP[n]=\frac{1}{n} * (1 + preSum[n-1] - preSum[1])$.
时间复杂度：$O(n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    double nthPersonGetsNthSeat(int n) {
        vector<double> DP(n+1, 0);
        vector<double> preSum(n+1, 0);
        for(int i=1;i<=n;i++){
            DP[i]=1/(double)i;
            DP[i]+=1/(double)i * (preSum[i-1]-preSum[1]); //DP[1]用到preSum[0]-preSum[1]=0，以及DP[2]用到preSum[1]-preSum[1]=0刚好不会错
            preSum[i]+=DP[i]+preSum[i-1];
        }
        return DP[n];
    }
};

继续优化
由递推公式:$DP[n]=\frac{1}{n} * (1 + preSum[n-1] - preSum[1]), n \geq 2$
$DP[n+1]=\frac{1}{n+1} * (1 + preSum[n] - preSum[1])$
则$(n+1) * DP[n+1] - n * DP[n] = preSum[n]- preSum[n-1]=DP[n]$
所以$DP[n+1]==DP[n], n \geq 2$。
时间复杂度：$O(1)$

1
2
3
4
5
6
class Solution {
public:
    double nthPersonGetsNthSeat(int n) {
        return n==1?1:0.5;
    }
};

位DP

898. 子数组按位或操作

Description
我们有一个非负整数数组 A。
对于每个（连续的）子数组 B = [A[i], A[i+1], …, A[j]] （ i <= j），我们对 B 中的每个元素进行按位或操作，获得结果 $A[i] | A[i+1] | … | A[j]$。
返回可能结果的数量。 （多次出现的结果在最终答案中仅计算一次。）
Example
示例 1：
输入：[0]
输出：1
解释：
只有一个可能的结果 0 。

示例 2：
输入：[1,1,2]
输出：3
解释：
可能的子数组为 [1]，[1]，[2]，[1, 1]，[1, 2]，[1, 1, 2]。
产生的结果为 1，1，2，1，3，3 。
有三个唯一值，所以答案是 3 。

示例 3：
输入：[1,2,4]
输出：6
解释：
可能的结果是 1，2，3，4，6，以及 7 。
提示：
$1 <= A.length <= 50000$
$0 <= A[i] <= 10^9$
Program

1
2
3
4
5
6
Result[i,j]=A[i]|A[i+1]|...|A[j], i<=j
A: 1 2 3 4
1: [1]
2: [1, 2], [2]
3: [1, 2, 3], [2,3], [3]
4: [1, 2, 3, 4], [3, 4]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int subarrayBitwiseORs(vector<int>& A) {
        unordered_set<int> cur;
        unordered_set<int> result;
        unordered_set<int> tmp;
        for(int x: A){
            tmp.clear();
            for(int y:cur){
                tmp.insert(x|y);
            }
            tmp.insert(x);
            cur=tmp;
            for(int z:cur) result.insert(z);
        }
        return result.size();
    }
};

树形DP

337. 打家劫舍 III

Description
在上次打劫完一条街道之后和一圈房屋后，小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为“根”。 除了“根”之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫，房屋将自动报警。
计算在不触动警报的情况下，小偷一晚能够盗取的最高金额。
Example
示例 1:
输入: [3,2,3,null,3,null,1]

1
2
3
4
5
  3
 / \
2   3
 \   \
  3   1

输出: 7
解释: 小偷一晚能够盗取的最高金额 = 3 + 3 + 1 = 7.

示例 2:
输入: [3,4,5,1,3,null,1]

1
2
3
4
5
     3
   / \
  4   5
 / \   \
1   3   1

输出: 9
解释: 小偷一晚能够盗取的最高金额 = 4 + 5 = 9.
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    map<pair<TreeNode*, bool>, int> m;
    int dfs(TreeNode* root, bool isSteal){
        if(root==NULL) return 0;
        if(m.find(pair<TreeNode*,bool>(root, isSteal))!=m.end()){
            return m[make_pair(root, isSteal)];
        }
        if(isSteal){ //本节点可偷
            //偷
            int leftSum=dfs(root->left, !isSteal);
            int rightSum=dfs(root->right, !isSteal);
            int stealSum=leftSum+rightSum+root->val;
            //不偷
            leftSum=dfs(root->left, isSteal);
            rightSum=dfs(root->right, isSteal);
            int nstealSum=leftSum+rightSum;
            m[make_pair(root, isSteal)]=max(stealSum, nstealSum);
            return m[make_pair(root, isSteal)];
        }else{ //本节点不可偷
            int leftSum=dfs(root->left, !isSteal);
            int rightSum=dfs(root->right, !isSteal);
            m[make_pair(root, isSteal)]=leftSum+rightSum;
            return m[make_pair(root, isSteal)];
        }
    }
    int rob(TreeNode* root) {
        return max(dfs(root, true), dfs(root, false));
    }
};

树形DP
我们可以用 f(o)表示选择 o 节点的情况下，o 节点的子树上被选择的节点的最大权值和；
g(o) 表示不选择 o 节点的情况下，o 节点的子树上被选择的节点的最大权值和；l 和 r 代表 o 的左右孩子。

  • 当 o 被选中时，o 的左右孩子都不能被选中，故 o 被选中情况下子树上被选中点的最大权值和为 l 和 r 不被选中的最大权值和相加，即 $f(o) = g(l) + g(r); f(o)=g(l)+g(r)$。
  • 当 o 不被选中时，o 的左右孩子可以被选中，也可以不被选中。对于 o 的某个具体的孩子 x，它对 o 的贡献是 x 被选中和不被选中情况下权值和的较大值。故 $g(o) = \max { f(l) , g(l)}+\max{ f(r) , g(r) }g(o)=max{f(l),g(l)}+max{f(r),g(r)}$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    unordered_map <TreeNode*, int> f, g;

    void dfs(TreeNode* o) {
        if (!o) {
            return;
        }
        dfs(o->left);
        dfs(o->right);
        f[o] = o->val + g[o->left] + g[o->right];
        g[o] = max(f[o->left], g[o->left]) + max(f[o->right], g[o->right]);
    }

    int rob(TreeNode* o) {
        dfs(o);
        return max(f[o], g[o]);
    }
};

优化
假设二叉树的节点个数为 nn。

我们可以看出，以上的算法对二叉树做了一次后序遍历，时间复杂度是 O(n)；由于递归会使用到栈空间，空间代价是 O(n)，哈希映射的空间代价也是 O(n)，故空间复杂度也是 O(n)。

我们可以做一个小小的优化，我们发现无论是f(o) 还是 g(o)，他们最终的值只和 f(l)、g(l)、f(r)、g(r) 有关，所以对于每个节点，我们只关心它的孩子节点们的 f 和 g 是多少。我们可以设计一个结构，表示某个节点的 f 和 g 值，在每次递归返回的时候，都把这个点对应的 f 和 g 返回给上一级调用，这样可以省去哈希映射的空间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
struct SubtreeStatus {
    int selected;
    int notSelected;
};

class Solution {
public:
    SubtreeStatus dfs(TreeNode* o) {
        if (!o) {
            return {0, 0};
        }
        auto l = dfs(o->left);
        auto r = dfs(o->right);
        int selected = o->val + l.notSelected + r.notSelected;
        int notSelected = max(l.selected, l.notSelected) + max(r.selected, r.notSelected);
        return {selected, notSelected};
    }

    int rob(TreeNode* o) {
        auto rootStatus = dfs(o);
        return max(rootStatus.selected, rootStatus.notSelected);
    }
};

834. 树中距离之和

Description
给定一个无向、连通的树。树中有 N 个标记为 0…N-1 的节点以及 N-1 条边 。
第 i 条边连接节点 edges[i][0] 和 edges[i][1] 。
返回一个表示节点 i 与其他所有节点距离之和的列表 ans。
Example
示例 1:
输入: N = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
输出: [8,12,6,10,10,10]
解释:
如下为给定的树的示意图：

1
2
3
4
5
  0
 / \
1   2
   /|\
  3 4 5

我们可以计算出 dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
也就是 1 + 1 + 2 + 2 + 2 = 8。 因此，answer[0] = 8，以此类推。
说明: 1 <= N <= 10000
Program
详见高赞题解
思路
（1）设distSum[root]为以root为根的子树root距离子树其他节点的距离和，递推公式：
$distSum[root]=\sum{(dist[Sum[child]]+nodeNum[child])}$
其中nodeNum[root]为以root为根的子节点个数。
明显后序遍历自底而上更新distSum[root]；
（2）以distSum[root]表示root距离其他所有节点（包括非子树的其他节点）的距离和：
可以看到整个树的根distSum[root]一定是最终所求，而其他所有节点的distSum[i]则是部分距离和（i距离其子树其他节点的距离和），以现有结果更新distSum[i]得到其最终所求：
root到除了以child为根的子树的距离和为$distSum[root]-nodeNum[child]-distSum[child]=S$，此时的distSum[root]为最终所求，distSum[child]为部分距离和；
则$S+N-nodeNum[child+distSum[child]$为最终的distSum[child]（child到其他所有节点的距离和）；
即$distSum[child]=distSum[root]-nodeNum[child]+N-nodeNum[child]$
前序遍历更新distSum[child]即可
（3）由于0未必是整个树的根结点，所以构建领接表时，需要双向连通，然后以0为根结点进行计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
public:
    vector<vector<int>> Adj;
    vector<int> nodeNum;
    vector<int> distSum;
    int N;
    void postOrder(int root, int parent){ //自底而上
        for(int i=0;i<Adj[root].size();i++){
            int child=Adj[root][i];
            if(child==parent) continue; //排除连接根的那条边
            postOrder(child, root);
            nodeNum[root]+=nodeNum[child];
            distSum[root]+=distSum[child];
        }
        distSum[root]+=nodeNum[root];
        nodeNum[root]+=1;
    }
    void preOrder(int root, int parent){ //自顶而下
        for(int i=0;i<Adj[root].size();i++){
            int child=Adj[root][i];
            if(child==parent) continue;
            distSum[child]=distSum[root]-nodeNum[child]+N-nodeNum[child]; //得到最终的距离和
            preOrder(child, root);
        }
    }
    vector<int> sumOfDistancesInTree(int N, vector<vector<int>>& edges) {
        this->N=N;
        Adj.resize(N);
        distSum.resize(N, 0);
        nodeNum.resize(N, 0);
        for(int i=0;i<N-1;i++){
            int u=edges[i][0], v=edges[i][1];
            Adj[u].push_back(v);  //不知道根为哪个节点，所以双向连通，以0作为根结点
            Adj[v].push_back(u);
        }
        postOrder(0, -1);
        preOrder(0, -1);
        return distSum;
    }
};

1130. 叶值的最小代价生成树

Description
给你一个正整数数组 arr，考虑所有满足以下条件的二叉树：

每个节点都有 0 个或是 2 个子节点。
数组 arr 中的值与树的中序遍历中每个叶节点的值一一对应。（知识回顾：如果一个节点有 0 个子节点，那么该节点为叶节点。）
每个非叶节点的值等于其左子树和右子树中叶节点的最大值的乘积。
在所有这样的二叉树中，返回每个非叶节点的值的最小可能总和。这个和的值是一个 32 位整数。
Example
示例：
输入：arr = [6,2,4]
输出：32
解释：
有两种可能的树，第一种的非叶节点的总和为 36，第二种非叶节点的总和为 32。

1
2
3
4
5
    24            24
   /  \          /  \
  12   4        6    8
 /  \               / \
6    2             2   4

提示：
2 <= arr.length <= 40
1 <= arr[i] <= 15
答案保证是一个 32 位带符号整数，即小于 2^31。
Program
动态规划
（1）首先数组元素顺序为二叉搜索树中序遍历时叶子节点顺序，而树中非叶子节点的值为左右子树最大叶子节点的乘积，可以发现需要计算左右子树的最大叶子结点；
（2）而每个子树的最大叶子节点为此子树所包含叶子的最大值，即数组[i,j]中最大的值！设M[i][j]为包含[i,j]叶子的子树中最大叶子值。
（3）题目要求树中节点只有0或2个孩子这两种情况，不包含只有一个孩子的节点！那么根据分治的思想，每棵子树至少包含一个叶子!；
（4）根据分治的思想，数组[0,n-1]这n个数可以划分成左右两部分，且每部分至少包含一个元素(叶子)，可以发现子问题也是[i.j]这j-i+1个数分成左右两部分，每部分至少包含一个元素(叶子)，现在就好办了；
（5）设DP[i][j]为所求[i,j]所组成的子树非叶子节点目标最小和，则状态转移方程为：
$DP[i][j]=max(M[i][k] * M[k+1][j] + DP[i][k] + DP[k+1][j]);$
注意边界DP[i][i]=0，即子树为叶子。
时间复杂度：$O(n^3)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    const int inf=0x3f3f3f3f;
    int mctFromLeafValues(vector<int>& arr) {
        int n=arr.size();
        int M[n][n];
        int DP[n][n];
        memset(M, 0, sizeof(M));
        memset(DP, inf, sizeof(DP));
        for(int i=0;i<n;i++){ //求[i,j]范围内最大元素值M[i][j]
            int ans=0;
            for(int j=i;j<n;j++){
                ans=max(ans, arr[j]);
                M[i][j]=ans;
            }
        }
        for(int i=n-1;i>=0;i--){
            for(int j=i;j<n;j++){
                if(i==j) {DP[i][j]=0;continue;} //单个叶子
                for(int k=i;k<j;k++){ //左右子树至少分得一个叶子
                    DP[i][j]=min(DP[i][j], M[i][k]*M[k+1][j]+DP[i][k]+DP[k+1][j]);
                }
            }
        }
        return DP[0][n-1];
    }
};

单调递减栈
通过贪心的思想，a,b,c为三个相邻的叶子，那么b肯定选择a,c中较小的组成一棵子树，然后去掉b，保留a,c再组成更高一层的子树。
如果a,b,c单调递减，那么情况不明，因为后续可能出现比c小的叶子，那么需要维护一个单调递减栈，即每个叶子与其左右相邻的叶子中较小的组成子树，得到的结果是最小的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    const int inf=0x3f3f3f3f;
    int mctFromLeafValues(vector<int>& arr) {
        int n=arr.size();
        stack<int> st;
        st.push(inf);
        int res=0;
        for(int x:arr){
            while(x>=st.top()){
                int oldTop=st.top();st.pop();
                res+=oldTop * min(x, st.top());
            }
            st.push(x);
        }
        while(st.size()>2){
            int oldTop=st.top();st.pop();
            res+=oldTop * st.top();
        }
        return res;
    }
};

1372. 二叉树中的最长交错路径

Description
给你一棵以 root 为根的二叉树，二叉树中的交错路径定义如下：

选择二叉树中 任意 节点和一个方向（左或者右）。
如果前进方向为右，那么移动到当前节点的的右子节点，否则移动到它的左子节点。
改变前进方向：左变右或者右变左。
重复第二步和第三步，直到你在树中无法继续移动。
交错路径的长度定义为：访问过的节点数目 - 1（单个节点的路径长度为 0 ）。

请你返回给定树中最长 交错路径 的长度。
Example
示例 1：
image
输入：root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1]
输出：3
解释：蓝色节点为树中最长交错路径（右 -> 左 -> 右）。

示例 2：
image
输入：root = [1,1,1,null,1,null,null,1,1,null,1]
输出：4
解释：蓝色节点为树中最长交错路径（左 -> 右 -> 左 -> 右）。

示例 3：
输入：root = [1]
输出：0
Program
深搜超时

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxLen=0;
    int dfs(TreeNode* root, int len, bool isRight){
        if(root==NULL) return len;
        maxLen=max(maxLen, ++len);
        int ans=0;
        if(!isRight) ans=dfs(root->left, len, true);
        if(isRight) ans=dfs(root->right, len, false);
        return ans;
    }
    void recur(TreeNode* root){
        if(root==NULL) return;
        dfs(root, 0, true);
        dfs(root, 0, false);
        recur(root->right);
        recur(root->left);
    }
    int longestZigZag(TreeNode* root) {
        recur(root);
        return maxLen-1;
    }
};

记忆化搜索
上述dfs有重复计算，比如一条交错路径上的所有节点都不必再次以其为根结点遍历了。
时间复杂度还是太高

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxLen=0;
    map<pair<TreeNode*, bool>, int> m;
    int dfs(TreeNode* root, int len, bool isRight){
        if(root==NULL) {
            maxLen=max(maxLen, len);
            return len;
        }
        if(m.find(pair<TreeNode*, bool>(root, isRight))!=m.end()) return m[pair<TreeNode*, bool>(root, isRight)];
        ++len;
        int ans=0;
        if(!isRight) ans=dfs(root->left, len, true);
        if(isRight) ans=dfs(root->right, len, false);
        m[pair<TreeNode*, bool>(root, isRight)]=ans;
        return ans;
    }
    void recur(TreeNode* root){
        if(root==NULL) return;
        dfs(root, 0, true);
        dfs(root, 0, false);
        recur(root->right);
        recur(root->left);
    }
    int longestZigZag(TreeNode* root) {
        recur(root);
        return maxLen-1;
    }
};

优化搜索
进一步分析可以发现，如果是一条交错路径，上述记忆化搜索没有必要，因为是交错路径无论从哪个节点遍历不会变长，只会变短！也就是说路径上的节点都不必再次遍历了。那么有可能有更长的路径就是从每个交错节点开始，朝原本方向反向交错的路径！
时间复杂度：$O(n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxLen=0;
    void dfs(TreeNode* root, int len, bool isRight){
        if(root==NULL) {maxLen=max(maxLen, len);return;}
        if(!isRight){
            dfs(root->left, len+1, true);
            dfs(root->right, 1, false);
        }
        if(isRight){
            dfs(root->right, len+1, false);
            dfs(root->left, 1, true);
        }
    }
    int longestZigZag(TreeNode* root) {
        dfs(root, 0, true);
        dfs(root, 0, false);
        return maxLen-1;
    }
};

树形DP
设leftDP[node]为以node为fahter左孩子且为交错路径终节点的长度，
rightDP[node]为以node为father右孩子且为交错路径终节点的长度。
则有：
leftDP[node]=rightDP[father]+1; //以当前节点为左孩子且为路径终点路径的长度为：其父节点(父节点是其父节点右孩子且为终结点)对应路径长度+1
rightDP[node]=leftDP[father]+1; //以当前节点为右孩子且为路径终点路径的长度为：其父节点(父节点是其父节点左孩子且为终结点)对应路径长度+1
时间复杂度：$O(n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int longestZigZag(TreeNode* root) {
        unordered_map<TreeNode*, int> leftDP, rightDP;
        leftDP[root]=rightDP[root]=0;
        queue<pair<TreeNode*,TreeNode*>> q;
        q.push({NULL, root});
        int ans=0;
        while(!q.empty()){
            pair<TreeNode*,TreeNode*> p=q.front();q.pop();
            TreeNode* father=p.first;
            TreeNode* node=p.second;
            if(father!=NULL){
                if(father->left==node) {
                    leftDP[node]=rightDP[father]+1;
                    ans=max(ans, leftDP[node]);
                }
                if(father->right==node) {
                    rightDP[node]=leftDP[father]+1;
                    ans=max(ans, rightDP[node]);
                }
            }
            if(node->left!=NULL) q.push({node, node->left});
            if(node->right!=NULL) q.push({node, node->right});
        }
        return ans;
    }
};

环状DP

873. 最长的斐波那契子序列的长度

Description
如果序列 X_1, X_2, …, X_n 满足下列条件，就说它是 斐波那契式 的：

  • n >= 3
  • 对于所有 i + 2 <= n，都有 X_i + X_{i+1} = X_{i+2}
    给定一个严格递增的正整数数组形成序列，找到 A 中最长的斐波那契式的子序列的长度。如果一个不存在，返回 0 。
    （回想一下，子序列是从原序列 A 中派生出来的，它从 A 中删掉任意数量的元素（也可以不删），而不改变其余元素的顺序。例如， [3, 5, 8] 是 [3, 4, 5, 6, 7, 8] 的一个子序列）

Example
示例 1：
输入: [1,2,3,4,5,6,7,8]
输出: 5
解释:
最长的斐波那契式子序列为：[1,2,3,5,8] 。

示例 2：
输入: [1,3,7,11,12,14,18]
输出: 3
解释:
最长的斐波那契式子序列有：
[1,11,12]，[3,11,14] 以及 [7,11,18] 。

提示：
3 <= A.length <= 1000
1 <= A[0] < A[1] < … < A[A.length - 1] <= 10^9
（对于以 Java，C，C++，以及 C# 的提交，时间限制被减少了 50%）
Program
动态规划
（1）如果设DP[i]为以i为结尾的满足条件的序列长度，那么在更新的时候无法保证结果是对的：
即$DP[i]=max(DP[j]+DP[k]), j=0,1,…,i-1, A[i]-A[j]=A[k]$，即[k,j,i]满足序列后三个元素，但是以第k个元素为结尾的序列(假设其末尾三个元素为[m,n,k])，这里[n,k,j]未必满足题意！
（2）故设DP[j][i]表示以j,i为序列末尾两个元素的满足条件的序列长度，递推公式：
$DP[j][i]=DP[k][j]+1$,即[k,j]与[j,i]可以相连，注意DP[j][i]初始化为2，因为任意两个不同的数都可以，但是这里要求A[i]>A[j]，此题严格递增，无影响，全部初始化为2.
（3）现在来看(2)中是否存在(1)的问题，可以发现已经严格满足序列前两个元素之和等于后一个元素了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int lenLongestFibSubseq(vector<int>& A) {
        int n=A.size();
        unordered_map<int, int> index;
        for(int i=0;i<n;i++) index[A[i]]=i;
        int ans=0;
        int DP[n][n];
        for(int i=0;i<n;i++){
            fill(DP[i], DP[i]+n, 2); //初始化
            for(int j=0;j<i;j++){
                if(A[i]-A[j]<A[j]&&index.find(A[i]-A[j])!=index.end()){
                    int idx=index[A[i]-A[j]];
                    DP[j][i]=DP[idx][j]+1;
                    ans=max(ans, DP[j][i]);
                }
            }
        }
        return ans>=3?ans:0;
    }
};

446. 等差数列划分 II - 子序列

Description
如果一个数列至少有三个元素，并且任意两个相邻元素之差相同，则称该数列为等差数列。
例如，以下数列为等差数列:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
以下数列不是等差数列。
1, 1, 2, 5, 7
数组 A 包含 N 个数，且索引从 0 开始。该数组子序列将划分为整数序列 (P0, P1, …, Pk)，满足 0 ≤ P0 < P1 < … < Pk < N。
如果序列 A[P0]，A[P1]，…，A[Pk-1]，A[Pk] 是等差的，那么数组 A 的子序列 (P0，P1，…，PK) 称为等差序列。值得注意的是，这意味着 k ≥ 2。
函数要返回数组 A 中所有等差子序列的个数。
输入包含 N 个整数。每个整数都在 -231 和 231-1 之间，另外 0 ≤ N ≤ 1000。保证输出小于 231-1。
Example
示例：
输入：[2, 4, 6, 8, 10]
输出：7
解释：
所有的等差子序列为：
[2,4,6]
[4,6,8]
[6,8,10]
[2,4,6,8]
[4,6,8,10]
[2,4,6,8,10]
[2,6,10]
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& A) {
        if(A.size()<=2) return 0;
        int n=A.size();
        vector<unordered_map<long long,int>> dp(n);
        long long ans=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<i;j++){
                long long diff=(long long)A[i]-(long long)A[j];
                int s=0;
                if(dp[j].find(diff)!=dp[j].end()) s=dp[j][diff];
                dp[i][diff]+=s+1;
                ans+=s;
            }
        }
        return ans;
    }
};

1027. 最长等差数列

Description
给定一个整数数组 A，返回 A 中最长等差子序列的长度。
回想一下，A 的子序列是列表 A[i_1], A[i_2], …, A[i_k] 其中 0 <= i_1 < i_2 < … < i_k <= A.length - 1。并且如果 B[i+1] - B[i]( 0 <= i < B.length - 1) 的值都相同，那么序列 B 是等差的。
Example
示例 1：
输入：[3,6,9,12]
输出：4
解释：
整个数组是公差为 3 的等差数列。

示例 2：
输入：[9,4,7,2,10]
输出：3
解释：
最长的等差子序列是 [4,7,10]。

示例 3：
输入：[20,1,15,3,10,5,8]
输出：4
解释：
最长的等差子序列是 [20,15,10,5]。

提示：
2 <= A.length <= 2000
0 <= A[i] <= 10000
Program
思路
设DP[i][diff]为以i为结尾，diff为差的最长等差子序列的长度；
与最长上升子序列类似，状态转移方程:
$DP[i][diff]=max(DP[j][diff]+1)$,其中$j<i<n,A[i]-A[j]=diff$
初始化DP[i][diff]=1，因为单个元素组成的子序列长度为1，diff任意。
时间复杂度:$O(n^2)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int longestArithSeqLength(vector<int>& A) {
        int n=A.size();
        vector<vector<int>> dp(n, vector<int>(20001, 1));
        int res=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<i;j++){
                int diff=A[i]-A[j]+10000;
                dp[i][diff]=max(dp[i][diff], dp[j][diff]+1);
                res=max(res, dp[i][diff]);
            }
        }
        return res;
    }
};

多DP递推

1186. 删除一次得到子数组最大和

Description
给你一个整数数组，返回它的某个 非空 子数组（连续元素）在执行一次可选的删除操作后，所能得到的最大元素总和。
换句话说，你可以从原数组中选出一个子数组，并可以决定要不要从中删除一个元素（只能删一次哦），（删除后）子数组中至少应当有一个元素，然后该子数组（剩下）的元素总和是所有子数组之中最大的。
注意，删除一个元素后，子数组 不能为空。
请看示例：
Example
示例 1：
输入：arr = [1,-2,0,3]
输出：4
解释：我们可以选出 [1, -2, 0, 3]，然后删掉 -2，这样得到 [1, 0, 3]，和最大。

示例 2：
输入：arr = [1,-2,-2,3]
输出：3
解释：我们直接选出 [3]，这就是最大和。

示例 3：
输入：arr = [-1,-1,-1,-1]
输出：-1
解释：最后得到的子数组不能为空，所以我们不能选择 [-1] 并从中删去 -1 来得到 0。
我们应该直接选择 [-1]，或者选择 [-1, -1] 再从中删去一个 -1。

提示：
1 <= arr.length <= 10^5
-10^4 <= arr[i] <= 10^4
Program
思路
本题的关键点就是在于有无删除元素，这个用一个DP很难表示，所以用两个DP，即DP1和DP2，分别表示以第i个元素为结尾的不删除和删除一次的最大和！
（1）那么不删除的DP1就是平常的连续子数组最大和：$DP1[i]=max(DP[i-1]+arr[i], arr[i])$；
（2）而删除的DP2的状态转移方程为：$DP2[i]=max(DP1[i-1], DP2[i-1]+arr[i])$，max中前一项表示删除arr[i]，后一项表示在前i-1项中删除一个，保留arr[i]！！
这样思路就清晰了！
时间复杂度：$O(n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int maximumSum(vector<int>& arr) {
        if(arr.size()==1) return arr[0];
        int n=arr.size();
        int DP1[n]; //以arr[i]为结尾，不删除的最大和
        int DP2[n]; //以arr[i]为结尾，删除元素后的最大和（可能删除了自己）
        DP1[0]=arr[0];
        for(int i=1;i<n;i++) DP1[i]=max(DP1[i-1]+arr[i], arr[i]);
        DP2[0]=arr[0];
        DP2[1]=max(arr[0], arr[1]);
        for(int i=2;i<n;i++) DP2[i]=max(DP1[i-1], DP2[i-1]+arr[i]); //前一项为删除自己，后一项为删除了的元素非自己
        int res=INT_MIN;
        for(int i=0;i<n;i++){
            res=max(res, DP1[i]);
            res=max(res, DP2[i]);
        }
        return res;
    }
};

1262. 可被三整除的最大和

Description
给你一个整数数组 nums，请你找出并返回能被三整除的元素最大和。
Example
示例 1：
输入：nums = [3,6,5,1,8]
输出：18
解释：选出数字 3, 6, 1 和 8，它们的和是 18（可被 3 整除的最大和）。

示例 2：
输入：nums = [4]
输出：0
解释：4 不能被 3 整除，所以无法选出数字，返回 0。

示例 3：
输入：nums = [1,2,3,4,4]
输出：12
解释：选出数字 1, 3, 4 以及 4，它们的和是 12（可被 3 整除的最大和）。

提示：
1 <= nums.length <= 4 * 10^4
1 <= nums[i] <= 10^4
Program
设DP[i][3]为前i个元素总和为模3余0,1,2的最大和。
边界：DP[0][0]=0表示没有，DP[0][1]=INT_MIN表示无定义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    int maxSumDivThree(vector<int>& nums) {
        int n = nums.size();
        int dp[n+1][3];
        dp[0][0] = 0; dp[0][1] = INT_MIN; dp[0][2] = INT_MIN;

        for (int i = 1; i <= n; i++) {
            if (nums[i - 1] % 3 == 0) {
                dp[i][0] = max(dp[i - 1][0], dp[i - 1][0] + nums[i - 1]);
                dp[i][1] = max(dp[i - 1][1], dp[i - 1][1] + nums[i - 1]);
                dp[i][2] = max(dp[i - 1][2], dp[i - 1][2] + nums[i - 1]);
            }
            else if (nums[i - 1] % 3 == 1) {
                dp[i][0] = max(dp[i - 1][0], dp[i - 1][2] + nums[i - 1]);
                dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + nums[i - 1]);
                dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + nums[i - 1]);
            }
            else if (nums[i - 1] % 3 == 2) {
                dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + nums[i - 1]);
                dp[i][1] = max(dp[i - 1][1], dp[i - 1][2] + nums[i - 1]);
                dp[i][2] = max(dp[i - 1][2], dp[i - 1][0] + nums[i - 1]);
            }
        }
        return dp[n][0];
    }
};

特殊DP

312. 戳气球

Description
有 n 个气球，编号为0 到 n-1，每个气球上都标有一个数字，这些数字存在数组 nums 中。
现在要求你戳破所有的气球。如果你戳破气球 i ，就可以获得 nums[left] * nums[i] * nums[right] 个硬币。 这里的 left 和 right 代表和 i 相邻的两个气球的序号。注意当你戳破了气球 i 后，气球 left 和气球 right 就变成了相邻的气球。
求所能获得硬币的最大数量。
说明:
你可以假设 nums[-1] = nums[n] = 1，但注意它们不是真实存在的所以并不能被戳破。
0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100
Example
示例:
输入: [3,1,5,8]
输出: 167
解释: nums = [3,1,5,8] –> [3,5,8] –> [3,8] –> [8] –> []
coins = 315 + 358 + 138 + 181 = 167
Program
dfs
一般思路就是深搜，如下所示，然而分析发现存在重复计算！—— 画出树形图就会发现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int ans=INT_MIN;
    void dfs(vector<int> nums, int sum){
        if(nums.size()==0){
            ans=max(ans, sum);
            return;
        }
        for(int i=0;i<nums.size();i++){
            int s=(i-1>=0?nums[i-1]:1)*nums[i]*(i+1<nums.size()?nums[i+1]:1);
            vector<int> tmp=nums;
            tmp.erase(tmp.begin()+i);
            dfs(tmp, s+sum);
        }
    }
    int maxCoins(vector<int>& nums) {
        dfs(nums, 0);
        return ans;
    }
};

记忆化搜索
换个思路，直接剔除的方法太过复杂，可以逆向推理，先在原数组基础上添加头尾元素值为1，然后假设中间全为空，一个个插入！

  • left>=right-1, return 0;
  • vis[left][right]=max(vec[left]vec[k]vec[right]+dfs(left,k)+dfs(k, right))
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    class Solution {
    public:
        int n;
        vector<vector<int>> vis;
        vector<int> vec;
        int dfs(int left, int right){
            if(left>=right-1) return 0;
            if(vis[left][right]!=-1) return vis[left][right];
            for(int i=left+1;i<right;i++){
                int sum=vec[left]*vec[i]*vec[right];
                sum+=dfs(left, i)+dfs(i, right);
                vis[left][right]=max(vis[left][right], sum);
            }
            return vis[left][right];
        }
        int maxCoins(vector<int>& nums) {
            n=nums.size();
            vec.resize(n+2);
            vis.resize(n+2, vector<int>(n+2, -1));
            for(int i=1;i<=n;i++){
                vec[i]=nums[i-1];
            }
            vec[0]=vec[n+1]=1;
            return dfs(0, n+1);
        }
    };

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int n;
    vector<int> vec;
    int maxCoins(vector<int>& nums) {
        n=nums.size();
        vec.resize(n+2);
        for(int i=1;i<=n;i++){
            vec[i]=nums[i-1];
        }
        vec[0]=vec[n+1]=1;
        int DP[n+2][n+2];
        memset(DP, 0, sizeof(DP));
        for(int i=n+1;i>=0;i--){
            for(int j=i+1;j<=n+1;j++){
                for(int k=i+1;k<j;k++){
                    DP[i][j]=max(DP[i][j], vec[i]*vec[k]*vec[j]+DP[i][k]+DP[k][j]);
                }
            }
        }
        return DP[0][n+1];
    }
};

403. 青蛙过河

Description
一只青蛙想要过河。 假定河流被等分为 x 个单元格，并且在每一个单元格内都有可能放有一石子（也有可能没有）。 青蛙可以跳上石头，但是不可以跳入水中。
给定石子的位置列表（用单元格序号升序表示）， 请判定青蛙能否成功过河（即能否在最后一步跳至最后一个石子上）。 开始时， 青蛙默认已站在第一个石子上，并可以假定它第一步只能跳跃一个单位（即只能从单元格1跳至单元格2）。
如果青蛙上一步跳跃了 k 个单位，那么它接下来的跳跃距离只能选择为 k - 1、k 或 k + 1个单位。 另请注意，青蛙只能向前方（终点的方向）跳跃。
请注意：
石子的数量 ≥ 2 且 < 1100；
每一个石子的位置序号都是一个非负整数，且其 < 231；
第一个石子的位置永远是0。
Example
示例 1:
[0,1,3,5,6,8,12,17]
总共有8个石子。
第一个石子处于序号为0的单元格的位置, 第二个石子处于序号为1的单元格的位置,
第三个石子在序号为3的单元格的位置， 以此定义整个数组…
最后一个石子处于序号为17的单元格的位置。

返回 true。即青蛙可以成功过河，按照如下方案跳跃：
跳1个单位到第2块石子, 然后跳2个单位到第3块石子, 接着
跳2个单位到第4块石子, 然后跳3个单位到第6块石子,
跳4个单位到第7块石子, 最后，跳5个单位到第8个石子（即最后一块石子）。

示例 2:
[0,1,2,3,4,8,9,11]
返回 false。青蛙没有办法过河。
这是因为第5和第6个石子之间的间距太大，没有可选的方案供青蛙跳跃过去。
Program
思路
记忆化搜索，记录vis[startIdx][step]表示从索引startIdx开始跳step步长的搜索结果，-1,0,1分别表示未计算，不可达，可达！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int n;
    vector<vector<int>> vis; //0不可达，1可达，-1未计算
    int dfs(const vector<int>& stones, int startIdx, int step){
        if(vis[startIdx][step]!=-1) return vis[startIdx][step];
        bool isPass=false;
        for(int i=startIdx+1;i<n;i++){
            int sp=stones[i]-stones[startIdx];
            if(sp>=step-1&&sp<=step+1){
                isPass|=dfs(stones, i, sp);
                if(isPass) break;
            }
        }
        vis[startIdx][step]=(isPass||startIdx==n-1)?1:0;
        return vis[startIdx][step];
    }
    bool canCross(vector<int>& stones) {
        n=stones.size();
        vis.resize(n, vector<int>(n, -1));
        return dfs(stones, 0, 0) == 1;
    }
};

动态规划
map记录能够到每个石子位置key的前一次跳的部署value

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    bool canCross(vector<int>& stones) {
        int n=stones.size();
        unordered_map<int, unordered_set<int>> m;
        for(int x:stones) m[x]=unordered_set<int>();
        m[0].insert(0);
        for(int x:stones){
            for(int k:m[x]){
                for(int s=k-1;s<=k+1;s++){
                    if(s>0&&m.find(x+s)!=m.end()){
                        m[x+s].insert(s);
                    }
                }
            }
        }
        return m[stones[n-1]].size()>0;
    }
};

514. 自由之路

Description
电子游戏“辐射4”中，任务“通向自由”要求玩家到达名为“Freedom Trail Ring”的金属表盘，并使用表盘拼写特定关键词才能开门。
给定一个字符串 ring，表示刻在外环上的编码；给定另一个字符串 key，表示需要拼写的关键词。您需要算出能够拼写关键词中所有字符的最少步数。
最初，ring 的第一个字符与12:00方向对齐。您需要顺时针或逆时针旋转 ring 以使 key 的一个字符在 12:00 方向对齐，然后按下中心按钮，以此逐个拼写完 key 中的所有字符。
旋转 ring 拼出 key 字符 key[i] 的阶段中：
您可以将 ring 顺时针或逆时针旋转一个位置，计为1步。旋转的最终目的是将字符串 ring 的一个字符与 12:00 方向对齐，并且这个字符必须等于字符 key[i] 。
如果字符 key[i] 已经对齐到12:00方向，您需要按下中心按钮进行拼写，这也将算作 1 步。按完之后，您可以开始拼写 key 的下一个字符（下一阶段）, 直至完成所有拼写。
Example
示例：
image
输入: ring = “godding”, key = “gd”
输出: 4
解释:
对于 key 的第一个字符 ‘g’，已经在正确的位置, 我们只需要1步来拼写这个字符。
对于 key 的第二个字符 ‘d’，我们需要逆时针旋转 ring “godding” 2步使它变成 “ddinggo”。
当然, 我们还需要1步进行拼写。
因此最终的输出是 4。
提示：
ring 和 key 的字符串长度取值范围均为 1 至 100；
两个字符串中都只有小写字符，并且均可能存在重复字符；
字符串 key 一定可以由字符串 ring 旋转拼出。
Program
动态规划
（1）定义$dp[i][j]$表示从前往后拼写出key的第i个字符，ring的第j个字符与12:00方向对齐的最小步数
（2）只有当字符串ring的第j个字符与key的第i个字符相同时才能拼写出key的第i个字符，因此，对于key的第i个字符，需要考虑计算的ring的第j个字符只有key[i]在ring中出现的下标集合。
（3）对于ring的每个字符维护一个位置数组pos[j]，表示字符j在ring中出现的位置集合；
（4）状态转移方程：
$dp[i][j]=min_{k\in{pos[key[i-1]]}}{\lbrace dp[i-1][k] + min\lbrace abs(j-k), n -abs(j-k)\rbrace + 1\rbrace}$
其中$min{abs(j-k), n-abs(j-k)}+1$表示在当前第k个字符与12:00方向对齐时第j个字符旋转到12:00方向并按下拼写的最少步数。
时间复杂度：$O(mn^2)$,m为key的长度，n为ring的长度
空间复杂度：$O(mn)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    const int inf=0x3f3f3f3f;
    int findRotateSteps(string ring, string key) {
        int m=key.length(), n=ring.length();
        vector<int> pos[26];
        for(int i=0;i<n;i++){ //记录每个ring元素出现的位置
            pos[ring[i] - 'a'].push_back(i);
        }
        int dp[m][n];
        memset(dp, inf, sizeof(dp));
        for(int j:pos[key[0] - 'a']){
            dp[0][j]=min(j, n-j)+1;
        }
        for(int i=1;i<m;i++){
            for(int j:pos[key[i]- 'a']){
                for(int k:pos[key[i-1] -'a']){
                    dp[i][j]=min(dp[i][j], dp[i-1][k]+min(abs(j-k), n-abs(j-k))+1);
                }
            }
        }
        int ans=inf;
        for(int j=0;j<n;j++) ans=min(ans, dp[m-1][j]);
        return ans;
    }
};

546. 移除盒子

Description
给出一些不同颜色的盒子，盒子的颜色由数字表示，即不同的数字表示不同的颜色。
你将经过若干轮操作去去掉盒子，直到所有的盒子都去掉为止。每一轮你可以移除具有相同颜色的连续 k 个盒子（k >= 1），这样一轮之后你将得到 kk 个积分。
当你将所有盒子都去掉之后，求你能获得的最大积分和。
*Example**
示例：
输入：boxes = [1,3,2,2,2,3,4,3,1]
输出：23
解释：
[1, 3, 2, 2, 2, 3, 4, 3, 1]
—-> [1, 3, 3, 4, 3, 1] (33=9 分)
—-> [1, 3, 3, 3, 1] (11=1 分)
—-> [1, 1] (33=9 分)
—-> [] (22=4 分)

提示：
1 <= boxes.length <= 100
1 <= boxes[i] <= 100
Program
设DP[l][r][k]为区间[l,r]且右边有与r相同的相连k个元素 的分数，对于r来说有两种决策：
（1）直接删除r以及右边与其相连的k个相同元素，DP[l][r-1][0]+(k+1) * (k+1) —— DP[l][r-1][0]中k==0表示r及右边k个元素删除后，与r-1右边没有相连了。
（2）不删除r，将其与[l,r-1]中 某个与r相同的元素i 相连，DP[l][i][k+1]+DP[i+1][r][0] —— DP[l][i][k+1]表示r不删除与i相连了，而DP[i+1][r][0]为删除[i+1,r]这部分的分数，k==0表示右边没有与r相连的相同元素了，因为r及右边k个相同相连元素全部跳过区间[i+1,r]而直接与i相连了。
时间复杂度：$O(n^4)$，最坏情况下每个 DP(l, r, k) 被计算一次，每次状态转移需要 $O(n)$ 的时间复杂度。
空间复杂度：$O(n^3)$，dp 数组的空间代价是 $O(n^3)$，递归使用栈空间的代价为 $O(n)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    int DP[100][100][100];
    int removeBoxes(vector<int>& boxes) {
        memset(DP, 0, sizeof(DP));
        int n=boxes.size();
        return calPoints(boxes, 0, n-1, 0);
    }
    int calPoints(vector<int>& boxes, int left, int right, int k){
        if(left>right) return 0;
        if(DP[left][right][k]!=0) return DP[left][right][k];
        while(left<right&&boxes[right]==boxes[right-1]){
            right--;
            k++;
        }
        DP[left][right][k]=calPoints(boxes, left, right-1, 0) + (k+1)*(k+1);
        for(int i=left;i<right;i++){
            if(boxes[right]==boxes[i]){
                DP[left][right][k]=max(
                    DP[left][right][k],
                    calPoints(boxes, left, i, k+1) + calPoints(boxes, i+1, right-1, 0)
                );
            }
        }
        return DP[left][right][k];
    }
};

956. 最高的广告牌

Description
你正在安装一个广告牌，并希望它高度最大。这块广告牌将有两个钢制支架，两边各一个。每个钢支架的高度必须相等。
你有一堆可以焊接在一起的钢筋 rods。举个例子，如果钢筋的长度为 1、2 和 3，则可以将它们焊接在一起形成长度为 6 的支架。
返回广告牌的最大可能安装高度。如果没法安装广告牌，请返回 0。
Example
示例 1：
输入：[1,2,3,6]
输出：6
解释：我们有两个不相交的子集 {1,2,3} 和 {6}，它们具有相同的和 sum = 6。

示例 2：
输入：[1,2,3,4,5,6]
输出：10
解释：我们有两个不相交的子集 {2,3,5} 和 {4,6}，它们具有相同的和 sum = 10。

示例 3：
输入：[1,2]
输出：0
解释：没法安装广告牌，所以返回 0。

提示：
0 <= rods.length <= 20
1 <= rods[i] <= 1000
钢筋的长度总和最多为 5000
Program
深搜
一个很正常的思路，对于每个rods[i]，可以给左边、右边、丢弃，然后通过后缀进行剪枝，然而还是超时！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    int n;
    int resH;
    struct Node{
        int i, ls, rs;
        Node(){}
        Node(int _i, int _ls, int _rs):i(_i),ls(_ls),rs(_rs){}
    };
    vector<int> suffix;
    void dfs(vector<int>& rods, int i, int leftSum, int rightSum){
        if(i==n){
            if(leftSum==rightSum){
                resH=max(resH, leftSum);
            }
            return;
        }
        if(leftSum>rightSum&&suffix[i]+rightSum<leftSum) return;
        if(rightSum>leftSum&&suffix[i]+leftSum<rightSum) return;
        dfs(rods, i+1, leftSum+rods[i], rightSum);
        dfs(rods, i+1, leftSum, rightSum+rods[i]);
        dfs(rods, i+1, leftSum, rightSum);
    }
    int tallestBillboard(vector<int>& rods) {
        n=rods.size();
        resH=0;
        int sum=0;
        suffix.resize(n,0);
        for(int i=rods.size()-1;i>=0;i--){
            sum+=rods[i];
            suffix[i]=sum;
        }
        dfs(rods, 0, 0, 0);
        return resH;
    }
};

动态规划
设DP[i][j]为前i+1个元素的两个子集差为j的最大总和，例如[1,2,3]，DP[2][1]可以有{1,2},{2,3}，DP[2][1]为5；
状态转移方程：
（1）丢弃，DP[i][j]=max(DP[i][j],DP[i-1][j])，即与前一个相同；
（2）放入和较大的一方，DP[i][j+rods[i]]=max(DP[i][j+rods[i]], DP[i-1][j]+rods[i]);
（3）放入和较小的一方，DP[i][abs(j-rods[i])]=max(DP[i][abs(j-rods[i])], DP[i-1][j]+rods[i]);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    int tallestBillboard(vector<int>& rods) {
        if(rods.size()<=1) return 0;
        int n=rods.size();
        int sum=accumulate(rods.begin(), rods.end(), 0);
        int DP[n][sum+1];
        memset(DP, 0, sizeof(DP));
        int preSum=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<=preSum;j++){
                //差为j的和至少为j
                if(i>0&&DP[i-1][j]<j) continue;

                //丢弃
                DP[i][j]=max(DP[i][j], (i>0?DP[i-1][j]:0));

                //加到大的集合
                int k=j+rods[i];
                DP[i][k]=max(DP[i][k], (i>0?DP[i-1][j]:0)+rods[i]);

                //加到小的集合
                k=abs(j-rods[i]);
                DP[i][k]=max(DP[i][k], (i>0?DP[i-1][j]:0)+rods[i]);
            }
            preSum+=rods[i];
        }
        return DP[n-1][0]/2;
    }
};

状态压缩

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    int tallestBillboard(vector<int>& rods) {
        if(rods.size()<=1) return 0;
        int n=rods.size();
        int sum=accumulate(rods.begin(), rods.end(), 0);
        vector<int> DP(sum+1, 0);
        int preSum=0;
        for(int i=0;i<n;i++){
            vector<int> newDP(sum+1, 0);
            for(int j=0;j<=preSum;j++){
                //差为j的和至少为j
                if(i>0&&DP[j]<j) continue;

                //丢弃
                newDP[j]=max(newDP[j], DP[j]);

                //加到大的集合
                int k=j+rods[i];
                newDP[k]=max(newDP[k], DP[j]+rods[i]);

                //加到小的集合
                k=abs(j-rods[i]);
                newDP[k]=max(newDP[k], DP[j]+rods[i]);
            }
            preSum+=rods[i];
            swap(DP, newDP);
        }
        return DP[0]/2;
    }
};

1631. 最小体力消耗路径

Description
你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。
Example
示例 1：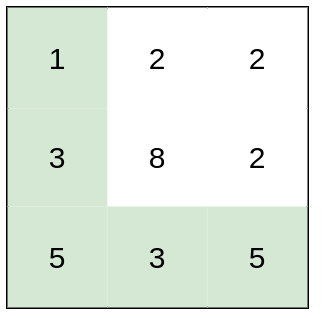
image
输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路劲差值最大值为 3 。

示例 2：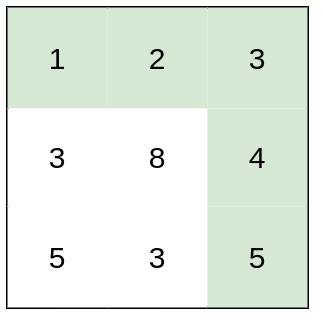
image
输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

示例 3：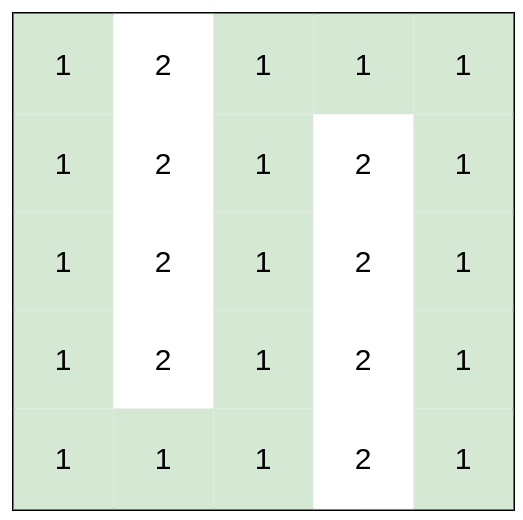
image
输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

提示：
rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 106
Program
思路
（1）设DP[i][j]为从[0][0]到[i][j]路径的最小体力消耗；
（2）通过优先队列广搜更新DP值，出队列的元素用vis标记；
（3）因为可能同时搜索到同一个位置[i][j]，更新DP[i][j]，所以优先队列，根据DP值更小的先出队列；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution {
public:
    const int inf=0x3f3f3f3f;
    const int steps[4][2]={
        -1, 0,
        1, 0,
        0, -1,
        0, 1
    };
    vector<vector<int>> DP;
    vector<vector<bool>> vis;
    struct Node{
        int x, y;
        int dis;
        Node(){}
        Node(int _x, int _y, int _dis){
            x=_x;
            y=_y;
            dis=_dis;
        }
        bool operator < (const Node& other) const{
            return dis>other.dis;
        }
    };
    priority_queue<Node> pq;
    int minimumEffortPath(vector<vector<int>>& heights) {
        int m=heights.size(), n=heights[0].size();
        DP.resize(m, vector<int>(n, inf));
        vis.resize(m, vector<bool>(n, false));
        DP[0][0]=0;
        pq.push(Node(0, 0, 0));
        while(!pq.empty()){
            Node node=pq.top(); pq.pop();
            if(vis[node.x][node.y]) continue;
            int x=node.x, y=node.y;
            vis[x][y]=true;
            for(int i=0;i<4;i++){
                int new_x=x+steps[i][0];
                int new_y=y+steps[i][1];
                if(new_x>=0&&new_x<m&&new_y>=0&&new_y<n&&!vis[new_x][new_y]){
                    int d=max(node.dis, abs(heights[x][y]-heights[new_x][new_y]));
                    DP[new_x][new_y]=min(d, DP[new_x][new_y]);
                    pq.push(Node(new_x, new_y, DP[new_x][new_y]));
                }
            }
        }
        return DP[m-1][n-1];
    }
};

状态压缩DP

464. 我能赢吗

Description
在 “100 game” 这个游戏中，两名玩家轮流选择从 1 到 10 的任意整数，累计整数和，先使得累计整数和达到 100 的玩家，即为胜者。
如果我们将游戏规则改为 “玩家不能重复使用整数” 呢？
例如，两个玩家可以轮流从公共整数池中抽取从 1 到 15 的整数（不放回），直到累计整数和 >= 100。
给定一个整数 maxChoosableInteger （整数池中可选择的最大数）和另一个整数 desiredTotal（累计和），判断先出手的玩家是否能稳赢（假设两位玩家游戏时都表现最佳）？
你可以假设 maxChoosableInteger 不会大于 20， desiredTotal 不会大于 300。
Example
示例：
输入：
maxChoosableInteger = 10
desiredTotal = 11
输出：
false
解释：
无论第一个玩家选择哪个整数，他都会失败。
第一个玩家可以选择从 1 到 10 的整数。
如果第一个玩家选择 1，那么第二个玩家只能选择从 2 到 10 的整数。
第二个玩家可以通过选择整数 10（那么累积和为 11 >= desiredTotal），从而取得胜利.
同样地，第一个玩家选择任意其他整数，第二个玩家都会赢。
Program
DP[num][total]=!DP[num|i][total-i] if i<total else 1;
num用二进制表示共有maxChoosableInteger位，选择了i则其第i-1为数字为1，表示已选。
DP[num][total]表示当前选取的num组合下先手在total下的输赢情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
private:
    bool helper(vector<int>& vis, int num, int mvalue, int total){
        if(vis[num]!=-1) return vis[num];

        for(int i=0;i<mvalue;i++){
            int cur=(1<<i); //选择i+1
            if((num&cur)) continue;
            if(i+1>=total){
                vis[num]=1;
                break;
            }
            bool next=helper(vis, (num|cur), mvalue, total-i-1);
            if(next==false){
                vis[num]=1;
                break;
            }
        }
        if(vis[num]==-1) vis[num]=0;
        return vis[num];
    }
public:
    bool canIWin(int maxChoosableInteger, int desiredTotal) {
        if((maxChoosableInteger*(maxChoosableInteger+1)/2)<desiredTotal) return false;
        vector<int> vis((1<<maxChoosableInteger)-1, -1); //-1没计算，0和1代表计算后不能赢和能赢
        int num=0;
        return helper(vis, num, maxChoosableInteger, desiredTotal);
    }
};

526. 优美的排列

Description
假设有从 1 到 N 的 N 个整数，如果从这 N 个数字中成功构造出一个数组，使得数组的第 i 位 (1 <= i <= N) 满足如下两个条件中的一个，我们就称这个数组为一个优美的排列。条件：

第 i 位的数字能被 i 整除
i 能被第 i 位上的数字整除
现在给定一个整数 N，请问可以构造多少个优美的排列？
Example
示例1:
输入: 2
输出: 2
解释:
第 1 个优美的排列是 [1, 2]:
第 1 个位置（i=1）上的数字是1，1能被 i（i=1）整除
第 2 个位置（i=2）上的数字是2，2能被 i（i=2）整除

第 2 个优美的排列是 [2, 1]:
第 1 个位置（i=1）上的数字是2，2能被 i（i=1）整除
第 2 个位置（i=2）上的数字是1，i（i=2）能被 1 整除
说明:
N 是一个正整数，并且不会超过15。
Program

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<bool> vis;
    int n;
    int ans=0;
    void dfs(int s){
        if(s==n){
            ans++;
            return;
        }
        for(int i=1;i<=n;i++){
            if(!vis[i]){
                if(((s+1)%i==0)||(i%(s+1)==0)){
                    vis[i]=true;
                    dfs(s+1);
                    vis[i]=false;
                }
            }
        }
    }
    int countArrangement(int N) {
        n=N;
        vis.resize(n+1, false);
        dfs(0);
        return ans;
    }
};

状态压缩DP
设DP[i]为排列i的个数，其中i用二进制表示，例如1011表示数1,2,4被使用:
令j为待排列的数字(1…N)，那么i中第j-1位必须为0表示未用，状态转移方程：
DP[i|(1<<(j-1))]+=DP[i]，当i的第j-1位未使用，且j与s成倍数关系（s为当前待排的第s个数）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int countArrangement(int N) {
        vector<int> DP(1<<N, 0);
        DP[0]=1;
        for(int i=0;i<(1<<N);i++){
            int s=0; //已经使用的个数
            for(int j=0;j<N;j++){
                s+=(i>>j)&1; //第j位是否为1,1表示使用，0表示未使用
            }
            s++;//正在使用的第s个数
            for(int j=1;j<=N;j++){ //遍历第s个数的可能值
                if(((i>>(j-1))&1)==0&&(j%s==0||s%j==0)){
                    DP[i|(1<<(j-1))]+=DP[i];
                }
            }
        }
        return DP[(1<<N)-1];
    }
};

698. 划分为k个相等的子集

Description
给定一个整数数组 nums 和一个正整数 k，找出是否有可能把这个数组分成 k 个非空子集，其总和都相等。
Example
示例 1：
输入： nums = [4, 3, 2, 3, 5, 2, 1], k = 4
输出： True
说明： 有可能将其分成 4 个子集（5），（1,4），（2,3），（2,3）等于总和。

提示：
1 <= k <= len(nums) <= 16
0 < nums[i] < 10000
Program
回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    vector<int> st;
    int k;
    int n;
    int target;
    bool helper(const vector<int>& nums, int i){ //每个元素都有k种选择
        if(i == n){
            for(int j = 0; j < k; j ++){
                if(st[j] != target) return false;
            }
            return true;
        }
        for(int j = 0; j < k; j ++){
            if(st[j] + nums[i] > target) continue;
            st[j] += nums[i];
            if(helper(nums, i + 1)) return true;
            st[j] -= nums[i];
        }
        return false;
    }
    bool canPartitionKSubsets(vector<int>& nums, int k) {
        st.resize(k, 0);
        target = accumulate(nums.begin(), nums.end(), 0);
        this -> k = k;
        n = nums.size();
        if(target % k != 0) return false;
        target /= k;
        sort(nums.begin(), nums.end(), greater<int>()); //大的值更容易确定位置，减少递归次数，否则超时
        return helper(nums, 0);
    }
};

状压DP
设dp[s]表示集合s能够组成的分组个数，st_sum[s]为集合s的和
状态转移方程：
当st_sum[s | (1 << i)] % target == 0时，dp[s | (1 << i)] = max(dp[s | (1 << i)], dp[s] + 1)；
否则，dp[s | (1 << i)] = max(dp[s | (1 << i)], dp[s])；
st_sum[s | (1 << i)] = st_sum[s] + nums[i];
时间复杂度：$O(2^n * n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    bool canPartitionKSubsets(vector<int>& nums, int k) {
        int n = nums.size();
        int target = accumulate(nums.begin(), nums.end(), 0);
        if(target % k != 0) return false;
        target /= k;
        vector<int> dp(1 << n, 0); //表示集合s能够构成的分组个数
        vector<int> st_sum(1 << n, 0); //集合s的和

        for(int s = 0; s < (1 << n); s ++){
            for(int i = 0; i < n; i ++){
                if((s & (1 << i)) != 0) continue; //集合s已经包含i
                int new_s = s | (1 << i);
                st_sum[new_s] = st_sum[s] + nums[i];
                if(st_sum[new_s] % target == 0) dp[new_s] = max(dp[new_s], dp[s] + 1);
                else dp[new_s] = max(dp[new_s], dp[s]);
            }
        }
        return dp[(1 << n) - 1] == k;
    }
};

1723. 完成所有工作的最短时间

Description
给你一个整数数组 jobs ，其中 jobs[i] 是完成第 i 项工作要花费的时间。
请你将这些工作分配给 k 位工人。所有工作都应该分配给工人，且每项工作只能分配给一位工人。工人的 工作时间 是完成分配给他们的所有工作花费时间的总和。请你设计一套最佳的工作分配方案，使工人的 最大工作时间 得以 最小化 。
返回分配方案中尽可能 最小 的 最大工作时间 。
Example
示例 1：
输入：jobs = [3,2,3], k = 3
输出：3
解释：给每位工人分配一项工作，最大工作时间是 3 。

示例 2：
输入：jobs = [1,2,4,7,8], k = 2
输出：11
解释：按下述方式分配工作：
1 号工人：1、2、8（工作时间 = 1 + 2 + 8 = 11）
2 号工人：4、7（工作时间 = 4 + 7 = 11）
最大工作时间是 11 。

提示：
1 <= k <= jobs.length <= 12
1 <= jobs[i] <= 107
Program
极大极小化/状压DP
设dp[k][s]为前k个工人，分配了二进制s集合任务(s中1的位置表示选择第i个任务)，状态转移方程：
$dp[k][s] = min(max(dp[k - 1][t], total[t]))$，其中t是s所有1的子集
total[i]表示集合i的总用时

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    const int inf = 0x3f3f3f3f;
    int minimumTimeRequired(vector<int>& jobs, int k) {
        int n =jobs.size();
        int dp[k][1 << n];
        memset(dp, 0, sizeof(dp));
        int total[1 << n]; //任务子集所耗的总时间
        memset(total, 0, sizeof(total));
        for(int i = 0; i < (1 << n); i ++ ){
            for(int j = 0; j < n; j ++ ){
                if((i & (1 << j)) == 0) continue; //i不包含j
                total[i] = total[i - (1 << j)] + jobs[j];
            }
        }
        for(int j = 0; j < (1 << n); j ++ ){
            dp[0][j] = total[j];
        }
        for(int i = 1; i < k; i ++ ){
            for(int s = 0; s < (1 << n); s ++ ){
                int minValue = inf;
                for(int t = s; t > 0; t = (t - 1) & s){ //枚举s的子集
                    int value = max(dp[i - 1][t], total[s - t]); //最大工作时间
                    minValue = min(minValue, value); //求所有可能值的最小值
                }
                dp[i][s] = minValue;
            }
        }
        return dp[k - 1][(1 << n) - 1];
    }
};

关联DP

1473. 粉刷房子 III

Program
在一个小城市里，有 m 个房子排成一排，你需要给每个房子涂上 n 种颜色之一（颜色编号为 1 到 n ）。有的房子去年夏天已经涂过颜色了，所以这些房子不需要被重新涂色。
我们将连续相同颜色尽可能多的房子称为一个街区。（比方说 houses = [1,2,2,3,3,2,1,1] ，它包含 5 个街区 [{1}, {2,2}, {3,3}, {2}, {1,1}] 。）
给你一个数组 houses ，一个 m * n 的矩阵 cost 和一个整数 target ，其中：
houses[i]：是第 i 个房子的颜色，0 表示这个房子还没有被涂色。
cost[i][j]：是将第 i 个房子涂成颜色 j+1 的花费。
请你返回房子涂色方案的最小总花费，使得每个房子都被涂色后，恰好组成 target 个街区。如果没有可用的涂色方案，请返回 -1 。
Example
示例 1：
输入：houses = [0,0,0,0,0], cost = [[1,10],[10,1],[10,1],[1,10],[5,1]], m = 5, n = 2, target = 3
输出：9
解释：房子涂色方案为 [1,2,2,1,1]
此方案包含 target = 3 个街区，分别是 [{1}, {2,2}, {1,1}]。
涂色的总花费为 (1 + 1 + 1 + 1 + 5) = 9。

示例 2：
输入：houses = [0,2,1,2,0], cost = [[1,10],[10,1],[10,1],[1,10],[5,1]], m = 5, n = 2, target = 3
输出：11
解释：有的房子已经被涂色了，在此基础上涂色方案为 [2,2,1,2,2]
此方案包含 target = 3 个街区，分别是 [{2,2}, {1}, {2,2}]。
给第一个和最后一个房子涂色的花费为 (10 + 1) = 11。

示例 3：
输入：houses = [0,0,0,0,0], cost = [[1,10],[10,1],[1,10],[10,1],[1,10]], m = 5, n = 2, target = 5
输出：5

示例 4：
输入：houses = [3,1,2,3], cost = [[1,1,1],[1,1,1],[1,1,1],[1,1,1]], m = 4, n = 3, target = 3
输出：-1
解释：房子已经被涂色并组成了 4 个街区，分别是 [{3},{1},{2},{3}] ，无法形成 target = 3 个街区。

提示：
m == houses.length == cost.length
n == cost[i].length
1 <= m <= 100
1 <= n <= 20
1 <= target <= m
0 <= houses[i] <= n
1 <= cost[i][j] <= 10^4
Program
动归
设dp[i][j][k]为刷第i个房子为颜色j属于第k个分区的最小花费，状态转移方程：
初始化dp[i][j][k]为inf；
当house[i] == 0未上色时，
$$
dp[i][j][k] = min(dp[i - 1][j][k], dp[i - 1][p][k - 1] + cost[i][j], p != j
$$
即前一个房子与当前房子颜色是否相同两种情况
当house[i] != 0已上色时，
$$
dp[i][j][k] = min(dp[i - 1][j][k], dp[i - 1][p][k - 1] , p != j
$$
边界：
当house[i] == 0未上色时，dp[0][j][0] = cost[0][j];
当house[i] != 0已上色且j == house[i]时，dp[0][j][0] = 0
时间复杂度：$O(m * n^2 * target)$
空间复杂度：$O(m * n * target)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    const int inf=0x3f3f3f3f;
    int minCost(vector<int>& houses, vector<vector<int>>& cost, int m, int n, int target) {
        int dp[m + 1][n + 1][target + 1];
        memset(dp, inf, sizeof(dp));
        //边界
        for(int j = 1; j <= n; j++ ){
            if(houses[0] != 0){ //已染色
                if(houses[0] == j) dp[1][j][1] = 0;
            }else dp[1][j][1] = cost[0][j - 1];
        }
        for(int i = 2; i <= m; i ++ ){
            for(int j = 1; j <= n; j ++){
                for(int k = 1; k <= target && k <= i; k ++ ){
                    int color = houses[i - 1];
                    if(color == 0){ //未染色
                        for(int p = 1; p <= n; p ++ ){
                            if(p == j) dp[i][j][k] = min(dp[i][j][k], dp[i - 1][j][k]);
                            else dp[i][j][k] = min(dp[i][j][k], dp[i - 1][p][k - 1]);
                        }
                        if(dp[i][j][k] != inf) dp[i][j][k] += cost[i - 1][j - 1];
                    }else{ //已染色
                        if(j != color) continue; //颜色不对
                        for(int p = 1; p <= n; p ++ ){
                            if(p == j) dp[i][j][k] = min(dp[i][j][k], dp[i - 1][j][k]);
                            else dp[i][j][k] = min(dp[i][j][k], dp[i - 1][p][k - 1]);
                        }
                    }
                }
            }
        }
        int ans = inf;
        for(int j = 1; j <= n; j ++ ){
            ans = min(ans, dp[m][j][target]);
        }
        return ans == inf ? -1 : ans;
    }
};

POJ

3616 Milking Time

Time Limit: 1000MS Memory Limit: 65536K
Total Submissions: 19649 Accepted: 8598

Description
Bessie is such a hard-working cow. In fact, she is so focused on maximizing her productivity that she decides to schedule her next $N (1 ≤ N ≤ 1,000,000)$ hours (conveniently labeled $0..N-1$) so that she produces as much milk as possible.

Farmer John has a list of $M$ ($1 ≤ M ≤ 1,000$) possibly overlapping intervals in which he is available for milking. Each interval i has a starting hour $(0 ≤ starting_houri ≤ N)$, an ending hour (starting_houri < ending_houri ≤ N), and a corresponding efficiency $(1 ≤ efficiencyi ≤ 1,000,000)$ which indicates how many gallons of milk that he can get out of Bessie in that interval. Farmer John starts and stops milking at the beginning of the starting hour and ending hour, respectively. When being milked, Bessie must be milked through an entire interval.

Even Bessie has her limitations, though. After being milked during any interval, she must rest R (1 ≤ R ≤ N) hours before she can start milking again. Given Farmer Johns list of intervals, determine the maximum amount of milk that Bessie can produce in the N hours.

Input

  • Line 1: Three space-separated integers: N, M, and R
  • Lines 2..M+1: Line i+1 describes FJ’s ith milking interval withthree space-separated integers: starting_houri , ending_houri , and efficiencyi

Output

  • Line 1: The maximum number of gallons of milk that Bessie can product in the N hours

Sample Input
12 4 2
1 2 8
10 12 19
3 6 24
7 10 31
Sample Output
43
Program
DP
设DP[i]为以i为结尾的最大分数，状态转移方程：DP[i]=max(DP[i], DP[j]+nums[i].w); 其中j为i左边与其不重叠的区间索引。
时间复杂度：$O(n^2)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<iostream>
#include<vector>
#include<cstring>
#include<algorithm>
using namespace std;
struct Node{
	int l, r, w;
	Node(){}
	Node(int _l, int _r, int _w):l(_l),r(_r),w(_w){}
	bool operator < (const Node& tmp) const{
		return l<tmp.l;
	}
};
int main(){
	int n,m,r;
	cin>>n>>m>>r;
	vector<Node> vec;
	for(int i=0;i<m;i++){
		int l,r,w;
		cin>>l>>r>>w;
		vec.push_back(Node(l,r,w));
	}
	sort(vec.begin(), vec.end());
	vector<int> DP(m, 0); //前i个的最大金额
	int ans=0;
	for(int i=0;i<m;i++){
		DP[i]=vec[i].w;//初始化
		for(int j=i-1;j>=0;j--){
			if(vec[j].r+r<=vec[i].l){
				DP[i]=max(DP[i], DP[j]+vec[i].w);
			}
		}
		ans=max(ans, DP[i]);
	}
	cout<<ans<<endl;
	return 0;
}

经典DP题

885. 螺旋矩阵 III

Description
给你 k 枚相同的鸡蛋，并可以使用一栋从第 1 层到第 n 层共有 n 层楼的建筑。
已知存在楼层 f ，满足 0 <= f <= n ，任何从 高于 f 的楼层落下的鸡蛋都会碎，从 f 楼层或比它低的楼层落下的鸡蛋都不会破。
每次操作，你可以取一枚没有碎的鸡蛋并把它从任一楼层 x 扔下（满足 1 <= x <= n）。如果鸡蛋碎了，你就不能再次使用它。如果某枚鸡蛋扔下后没有摔碎，则可以在之后的操作中 重复使用 这枚鸡蛋。
请你计算并返回要确定 f 确切的值 的 最小操作次数 是多少？
Example
示例 1：
输入：k = 1, n = 2
输出：2
解释：
鸡蛋从 1 楼掉落。如果它碎了，肯定能得出 f = 0 。
否则，鸡蛋从 2 楼掉落。如果它碎了，肯定能得出 f = 1 。
如果它没碎，那么肯定能得出 f = 2 。
因此，在最坏的情况下我们需要移动 2 次以确定 f 是多少。

示例 2：
输入：k = 2, n = 6
输出：3

示例 3：
输入：k = 3, n = 14
输出：4

提示：
1 <= k <= 100
1 <= n <= 104
Program
动态规划
设dp[i][k]表示i层k枚鸡蛋的最小操作次数：
（1）dp[0][k] = 0；
（2）dp[i][1] = i;
（3）试第j层，
①若摔碎，dp[i][k] = dp[j - 1][k - 1];
②若没摔碎，dp[i][k] = dp[i - j][k]
所以对于的那个j，dp[i][k]=max(dp[ j - 1][k - 1], dp[i - j][k]) + 1;
而对于每个j，有$1 <= j <= i$，dp[i][k] = min(max(dp[ j - 1][k - 1], dp[i - j][k])) + 1；
时间复杂度：$O(n^2 * k)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    const int inf = 0x3f3f3f3f;
    int superEggDrop(int K, int n) {
        if(n == 0 || K == 0) return 0;
        if(K == 1) return n;
        int dp[n + 1][K + 1];
        memset(dp, 0, sizeof(dp));
        for(int i = 1; i <= n; i ++) dp[i][1] = i;
        for(int i = 1; i <= n; i ++){
            for(int k = 2; k <= K; k ++){
                int minValue = inf;
                for(int j = 1; j <= i; j ++){
                    //cout << dp[j - 1][k - 1] << " " << dp[i - j][k] << " ";
                    minValue = min(minValue, max(dp[j - 1][k - 1], dp[i - j][k])) ;
                }
                dp[i][k] = minValue + 1;
                //cout << dp[i][k] << " ";
            }
            //cout << endl;
        }
        return dp[n][K];
    }
};

最优解
参考

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int superEggDrop(int K, int N) {
        if(K <= 0 || N <= 0) return 0;
        int btTimes = log2(N) + 1;
        if(K >= btTimes) return btTimes;
        vector<int> f(K + 1, 0), g(K + 1, 0);
        for(int j = 1; ; j ++){
            for(int i = 1; i <= K; i ++){
                f[i] = g[i] + g[i - 1] + 1;
                if(f[i] >= N) return j;
            }
            swap(f, g);
        }
        return -1;
    }
};
赏

Thank you for inviting me to have candy.

支付宝
微信

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

做一个安静细微的人，<br> 于角落里自在开放，<br> 默默悦人，<br> 却始终不引起过分热闹的关注，<br> 保有独立而随意的品格，<br> 这就很好。<br><br> Stick to what you insist on,<br> believe what you believe!<br> Life hastily for decades,<br> do what I can!