Bayesian Optimization

Installation

Pure Python implementation of bayesian global optimization with gaussian processes.

  • PyPI (pip):
    1
    $ pip install bayesian-optimization
  • Conda from conda-forge channel:
    1
    $ conda install -c conda-forge bayesian-optimization
    This is a constrained global optimization package built upon bayesian inference and gaussian process, that attempts to find the maximum value of an unknown function in as few iterations as possible. This technique is particularly suited for optimization of high cost functions, situations where the balance between exploration and exploitation is important.

    Basic Usage

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
from sklearn.datasets import make_classification
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
from bayes_opt import BayesianOptimization
from bayes_opt import JSONLogger
from bayes_opt import Events
import numpy as np

x, y = make_classification(n_samples=10000, n_features=10, n_classes=2)
rf = RandomForestClassifier(n_estimators=100)
print(np.mean(cross_val_score(rf, x, y, cv=20, scoring='roc_auc')))


# the function we want to optimize
def rf_cv(n_estimators, min_samples_split, max_features, max_depth):
    val = cross_val_score(
        RandomForestClassifier(n_estimators=int(n_estimators),
                               min_samples_split=int(min_samples_split),
                               max_features=min(max_features, 0.999),
                               max_depth=int(max_depth),
                               random_state=2),
        x, y, scoring='roc_auc', cv=5).mean()
    return val


# Define the optimizer
# f: the function to be optimized
# pbounds: the parameters of f
rf_bo = BayesianOptimization(
    f=rf_cv,
    pbounds={'n_estimators': (10, 250),
             'min_samples_split': (2, 25),
             'max_features': (0.1, 0.999),
             'max_depth': (5, 15)},
    random_state=2
)

# logger
logger = JSONLogger(path="./logs.json")
rf_bo.subscribe(Events.OPTIMIZATION_STEP, logger)
# The BayesianOptimization object will work out of the box without much tuning needed.
# The main method you should be aware of is maximize, which does exactly what you think it does.
# n_iter: How many steps of bayesian optimization you want to perform.
#   The more steps the more likely to find a good maximum you are.
# init_points: How many steps of random exploration you want to perform.
#   Random exploration can help by diversifying the exploration space.

# rf_bo.probe(
#     params={'n_estimators': 15,
#             'min_samples_split': 2,
#             'max_features': 0.2,
#             'max_depth': 10},
#     lazy=True
# )
rf_bo.maximize(n_iter=10, init_points=0)
# The best combination of parameters and target value found can be accessed via the property
# optimizer.max
print(rf_bo.max)

# While the list of all parameters probed and their corresponding target values
# is available via the property optimizer.res.
for i, res in enumerate(rf_bo.res):
    print("Iteration {}: \n\t{}".format(i, res))

Visualization

Target Function
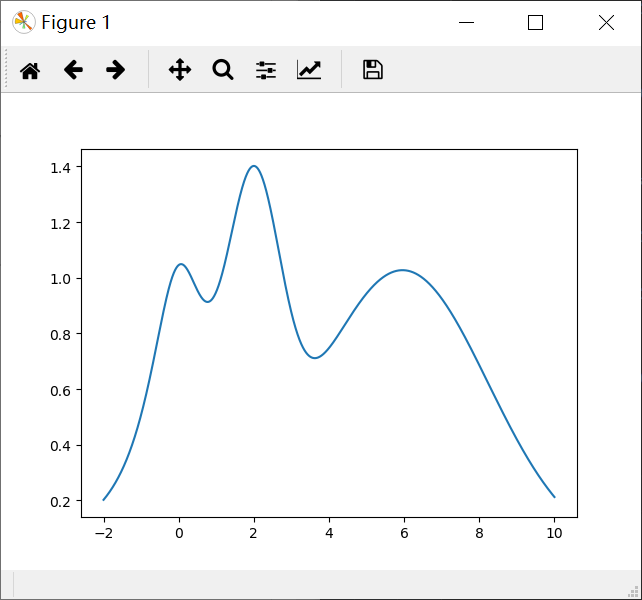
Lets create a target 1-D function with multiple local maxima to test and visualize how the BayesianOptimization package works. The target function we will try to maximize is the following:
$f(x)=e^{-(x-2)^2}+e^{-\frac{(x-6)^2}{10}}+\frac{1}{x^2+1}$
its maximum is at $x = 2$ and we will restrict the interval of interest to $x \in (-2, 10)$.
Notice that, in practice, this function is unknown, the only information we have is obtained by sequentialy probing it at different points. Bayesian Optimization works by contructing a posterior distribution of functions that best fit the data observed and chosing the next probing point by balancing exploration and exploitation.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
from bayes_opt import BayesianOptimization
from bayes_opt import UtilityFunction
import numpy as np

import matplotlib.pyplot as plt
from matplotlib import gridspec


# Target Function
def target(x):
    return np.exp(-(x - 2) ** 2) + np.exp(-(x - 6) ** 2 / 10) + 1 / (x ** 2 + 1)


x = np.linspace(-2, 10, 10000).reshape(-1, 1)
y = target(x)
# plt.plot(x, y)
# plt.show()

# Create a BayesianOptimization Object
optimizer = BayesianOptimization(f=target, pbounds={'x': (-2, 10)}, random_state=42)
# In this example we will use the Upper Confidence Bound (UCB) as our utility function.
# It has the free parameter $\kappa$ which control the balance between exploration and exploitation;
# we will set $\kappa=5$ which, in this case, makes the algorithm quite bold.
optimizer.maximize(init_points=0, n_iter=5, kappa=5)


# Plotting and visualizing the algorithm at each step
# Firstly, define a couple functions to make plotting easier
def posterior(optimizer, x_obs, y_obs, grid):
    optimizer._gp.fit(x_obs, y_obs)
    mu, sigma = optimizer._gp.predict(grid, return_std=True)
    return mu, sigma


def plot_gp(optimizer, x, y):
    fig = plt.figure(figsize=(16, 10))
    steps = len(optimizer.space)
    fig.suptitle(
        'Gaussian Process and Utility Function After {} Steps'.format(steps),
        fontdict={'size': 30}
    )

    # gs = gridspec.GridSpec(2, 1, height_ratios=[3, 1])
    gs = fig.add_gridspec(2, 1, height_ratios=[3, 1])
    axis = fig.add_subplot(gs[0])
    acq = fig.add_subplot(gs[1])
    # axis = plt.subplot(gs[0])
    # acq = plt.subplot(gs[1])

    x_obs = np.array([[res['params']['x']] for res in optimizer.res])
    y_obs = np.array([res['target'] for res in optimizer.res])

    mu, sigma = posterior(optimizer, x_obs, y_obs, x)
    # Target Function
    axis.plot(x, y, linewidth=3, label='Target')
    # Observation points
    axis.plot(x_obs.flatten(), y_obs, 'D', markersize=8, label=u'Observations', color='r')
    axis.plot(x, mu, '--', color='k', label='Prediction')

    axis.fill(np.concatenate([x, x[::-1]]),
              np.concatenate([mu - 1.9600 * sigma, (mu + 1.9600 * sigma)[::-1]]),
              alpha=.6, fc='c', ec='None', label='95% confidence interval')

    axis.set_xlim((-2, 10))
    axis.set_ylim((None, None))
    axis.set_ylabel('f(x)', fontdict={'size': 15})
    axis.set_xlabel('x', fontdict={'size': 15})

    utility_function = UtilityFunction(kind='ucb', kappa=5, xi=0)
    utility = utility_function.utility(x, optimizer._gp, 0)

    acq.plot(x, utility, label='Utility Function', color='purple')
    acq.plot(x[np.argmax(utility)], np.max(utility), '*', markersize=15,
             label=u'Next Best Guess', markerfacecolor='gold', markeredgecolor='k',
             markeredgewidth=1)
    acq.set_xlim((-2, 10))
    acq.set_ylim((0, np.max(utility) + 0.5))
    acq.set_ylabel('Utility', fontdict={'size': 15})
    acq.set_xlabel('x', fontdict={'size': 15})

    axis.legend(loc=2, bbox_to_anchor=(1.01, 1), borderaxespad=0.)
    acq.legend(loc=2, bbox_to_anchor=(1.01, 1), borderaxespad=0.)
    plt.show()


plot_gp(optimizer, x, y)

Stopping
After just a few points the algorithm was able to get pretty close to the true maximum. It is important to notice that the trade off between exploration (exploring the parameter space) and exploitation (probing points near the current known maximum) is fundamental to a succesful bayesian optimization procedure. The utility function being used here (Upper Confidence Bound - UCB) has a free parameter $\kappa$ that allows the user to make the algorithm more or less conservative. Additionally, the larger the initial set of random points explored, the less likely the algorithm is to get stuck in local minima due to being too conservative.

1
2
3
4
5
6
7
8
9
|   iter    |  target   |     x     |
-------------------------------------
|  1        |  1.214    |  2.494    |
|  2        |  0.2124   |  9.997    |
|  3        |  1.214    |  2.494    |
|  4        |  0.5096   | -0.9961   |
|  5        |  0.8271   |  4.403    |
|  6        |  0.8721   |  7.259    |
=====================================

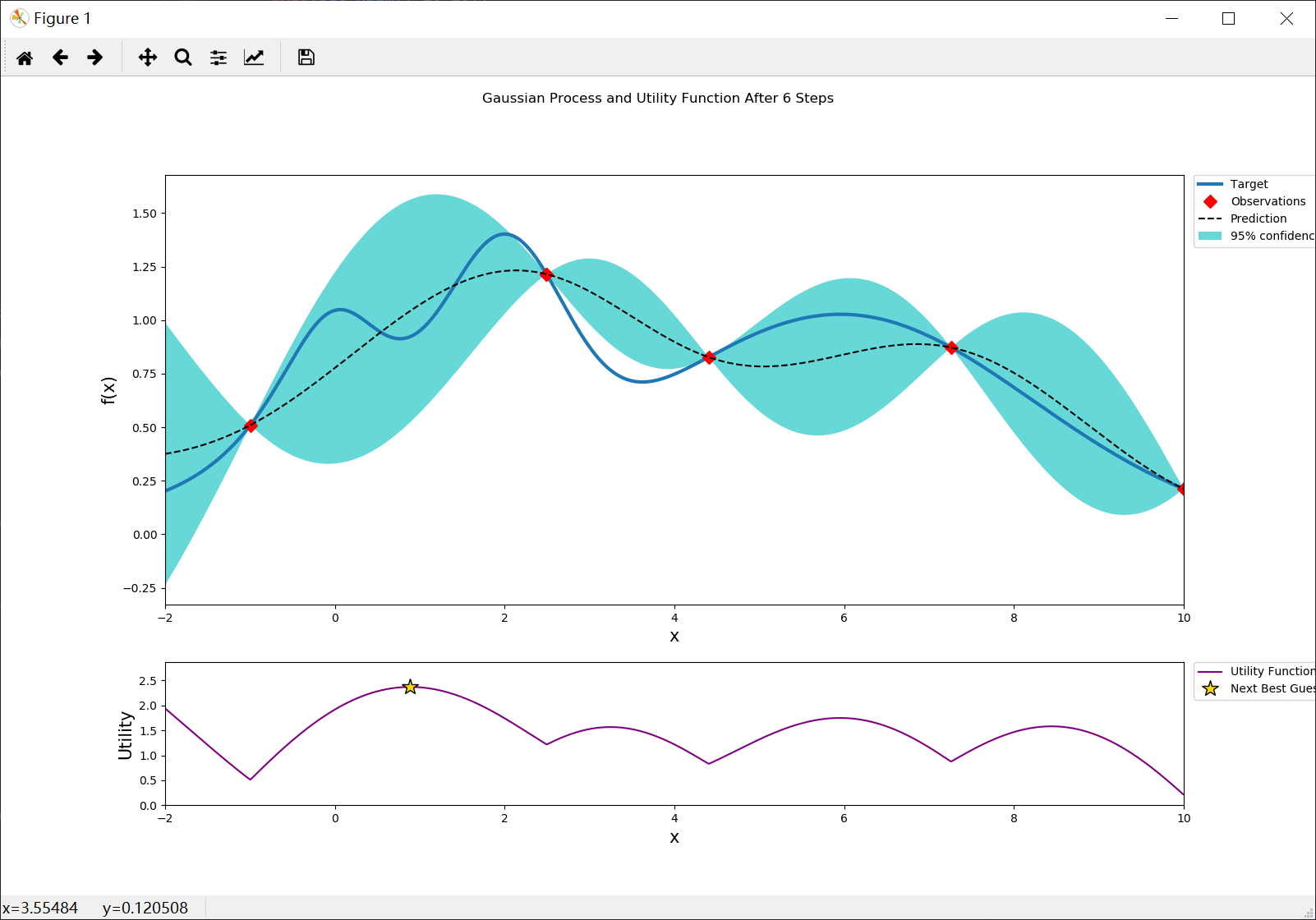
image

Exploitation vs Exploration

Target function

1
2
3
4
5
6
7
8
np.random.seed(42)
xs = np.linspace(-2, 10, 10000)

def f(x):
    return np.exp(-(x - 2) ** 2) + np.exp(-(x - 6) ** 2 / 10) + 1/ (x ** 2 + 1)

plt.plot(xs, f(xs))
plt.show()

image
Utility function for plotting

1
2
3
4
5
6
7
8
9
10
def plot_bo(f, bo):
    x = np.linspace(-2, 10, 10000)
    mean, sigma = bo._gp.predict(x.reshape(-1, 1), return_std=True)

    plt.figure(figsize=(16, 9))
    plt.plot(x, f(x))
    plt.plot(x, mean)
    plt.fill_between(x, mean + sigma, mean - sigma, alpha=0.1)
    plt.scatter(bo.space.params.flatten(), bo.space.target, c="red", s=50, zorder=10)
    plt.show()

Acquisition Function

Upper Confidence Bound (UCB)

Prefer exploitation (kappa=0.1)
Note that most points are around the peak(s).

1
2
3
4
5
6
7
8
9
10
bo = BayesianOptimization(
    f=f,
    pbounds={"x": (-2, 10)},
    verbose=0,
    random_state=987234,
)

bo.maximize(n_iter=10, acq="ucb", kappa=0.1)

plot_bo(f, bo)

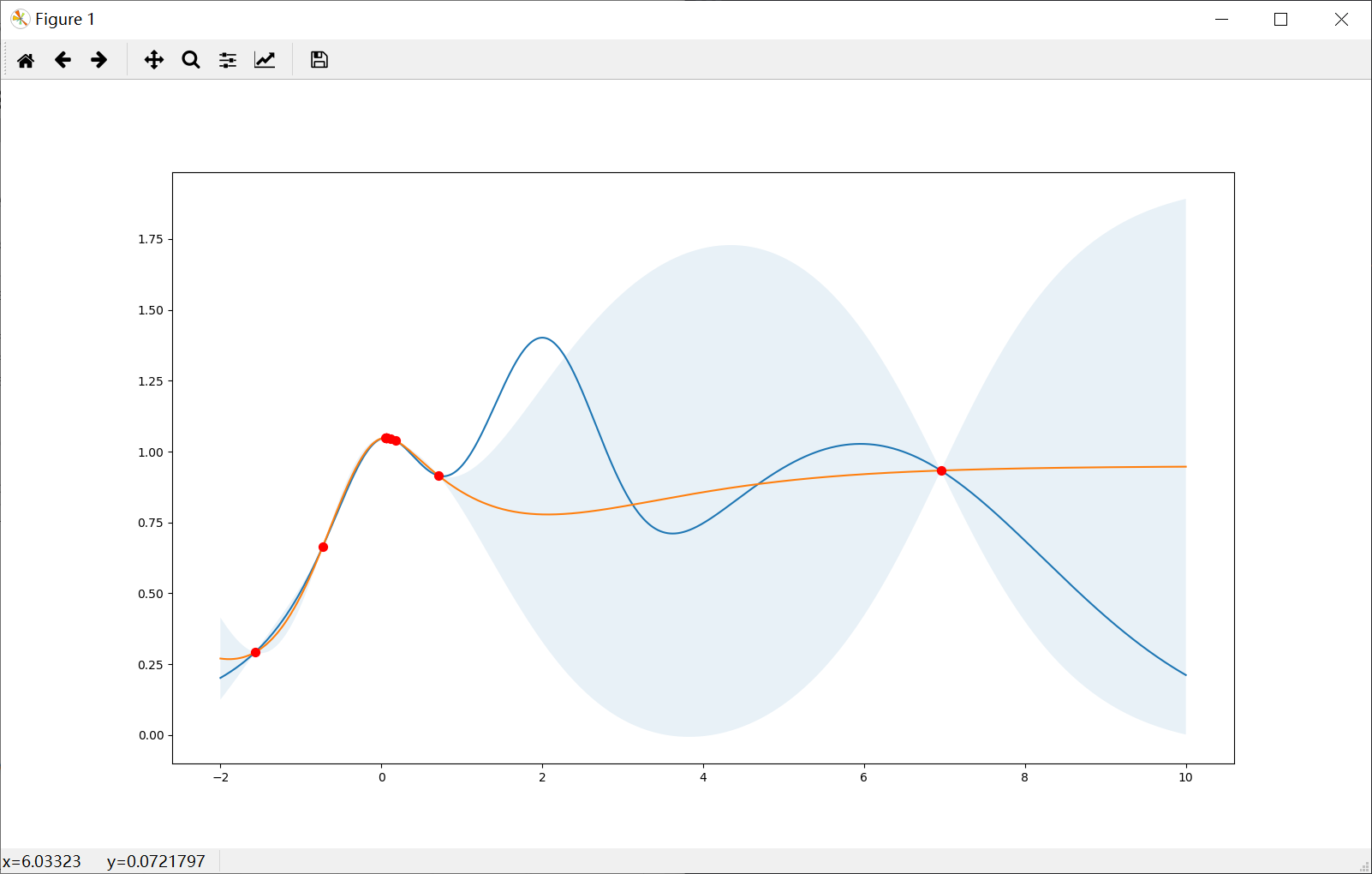
image
Prefer exploration (kappa=10)
Note that the points are more spread out across the whole range.

1
2
3
4
5
6
7
8
9
10
bo = BayesianOptimization(
    f=f,
    pbounds={"x": (-2, 10)},
    verbose=0,
    random_state=987234,
)

bo.maximize(n_iter=10, acq="ucb", kappa=10)

plot_bo(f, bo)

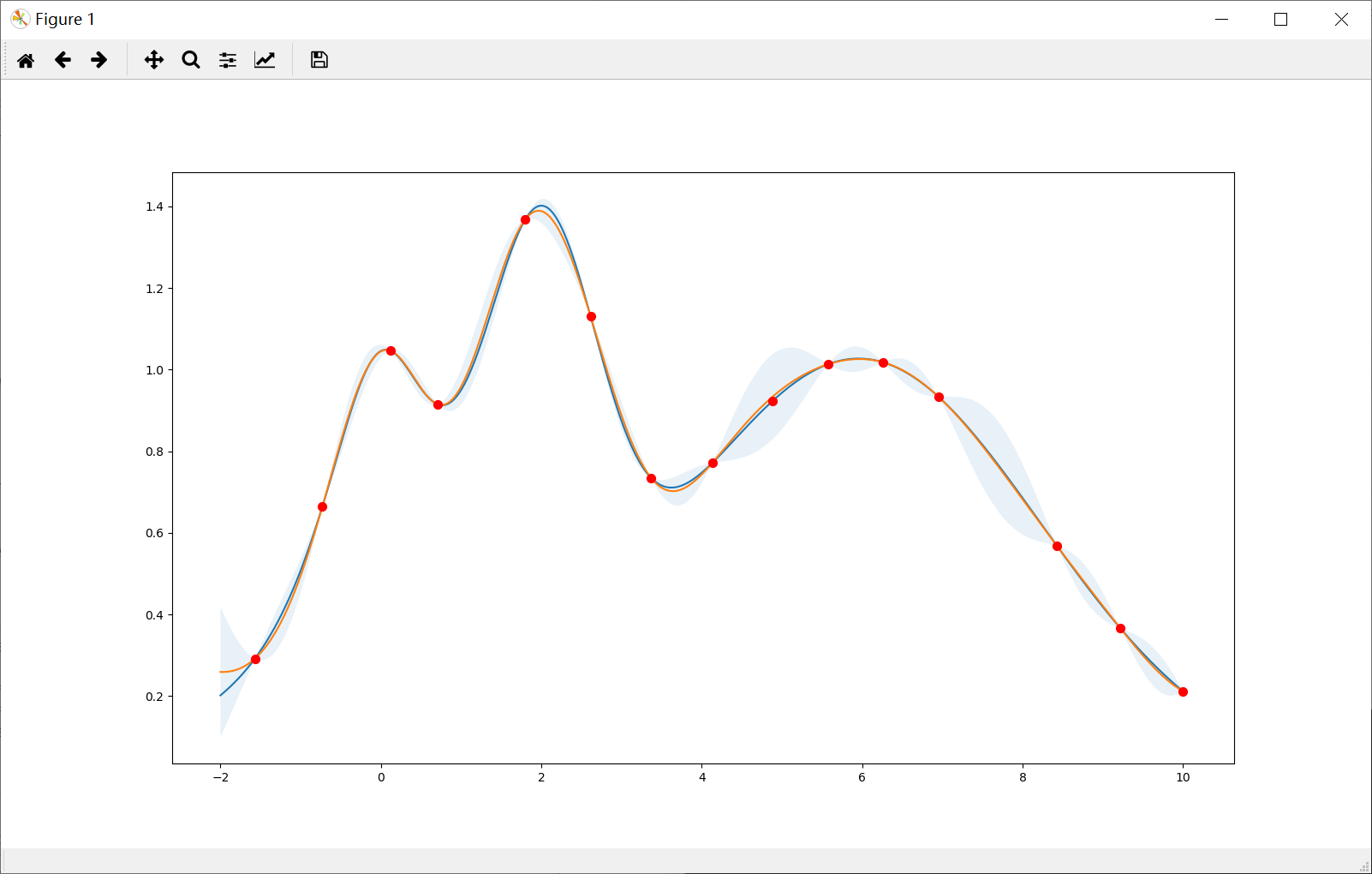
image

Expected Improvement (EI)

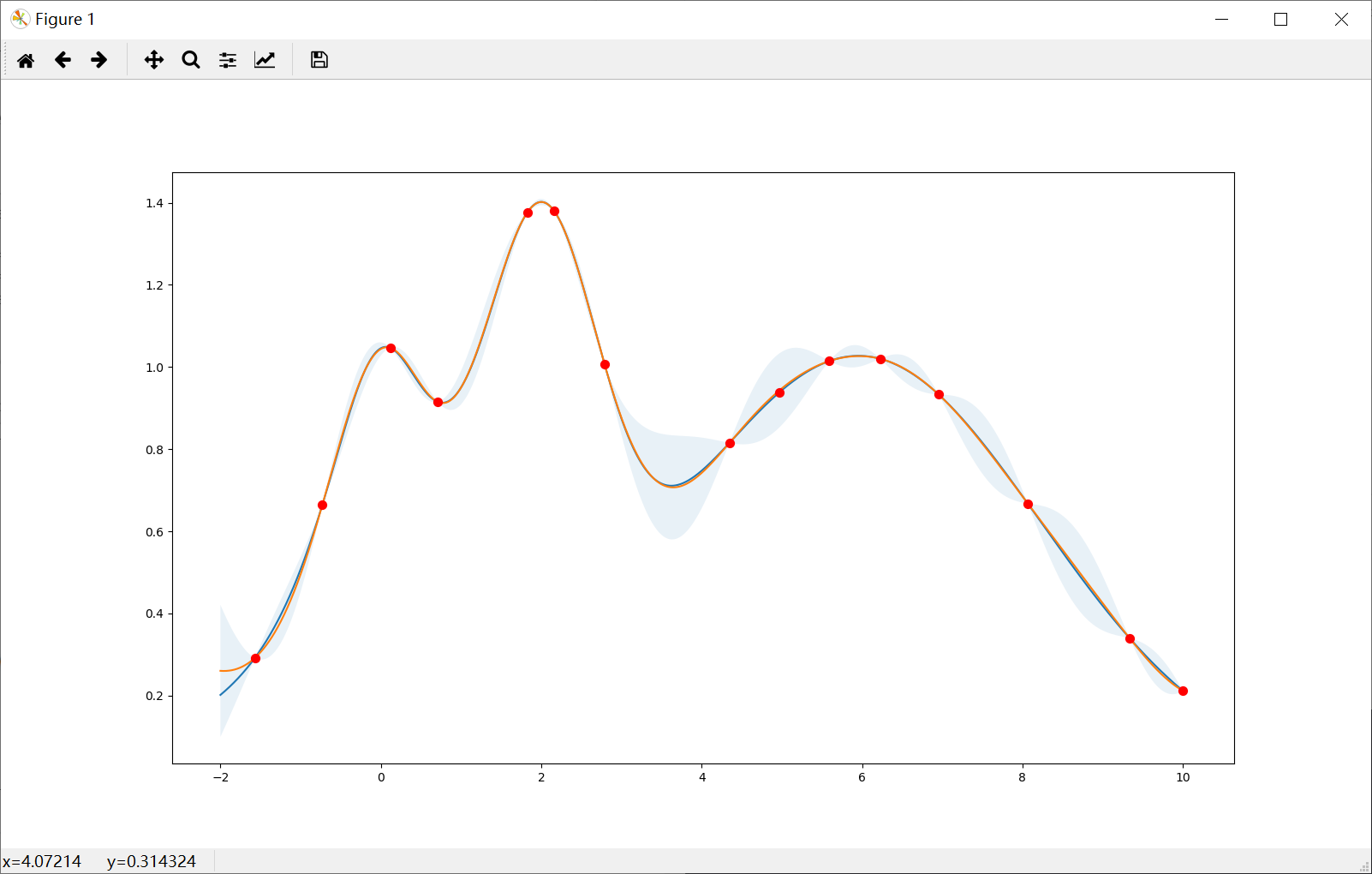
Prefer exploitation (xi=1e-4)
Note that most points are around the peak(s).

1
2
3
4
5
6
7
8
9
10
bo = BayesianOptimization(
    f=f,
    pbounds={"x": (-2, 10)},
    verbose=0,
    random_state=987234,
)

bo.maximize(n_iter=10, acq="ei", xi=1e-4)

plot_bo(f, bo)

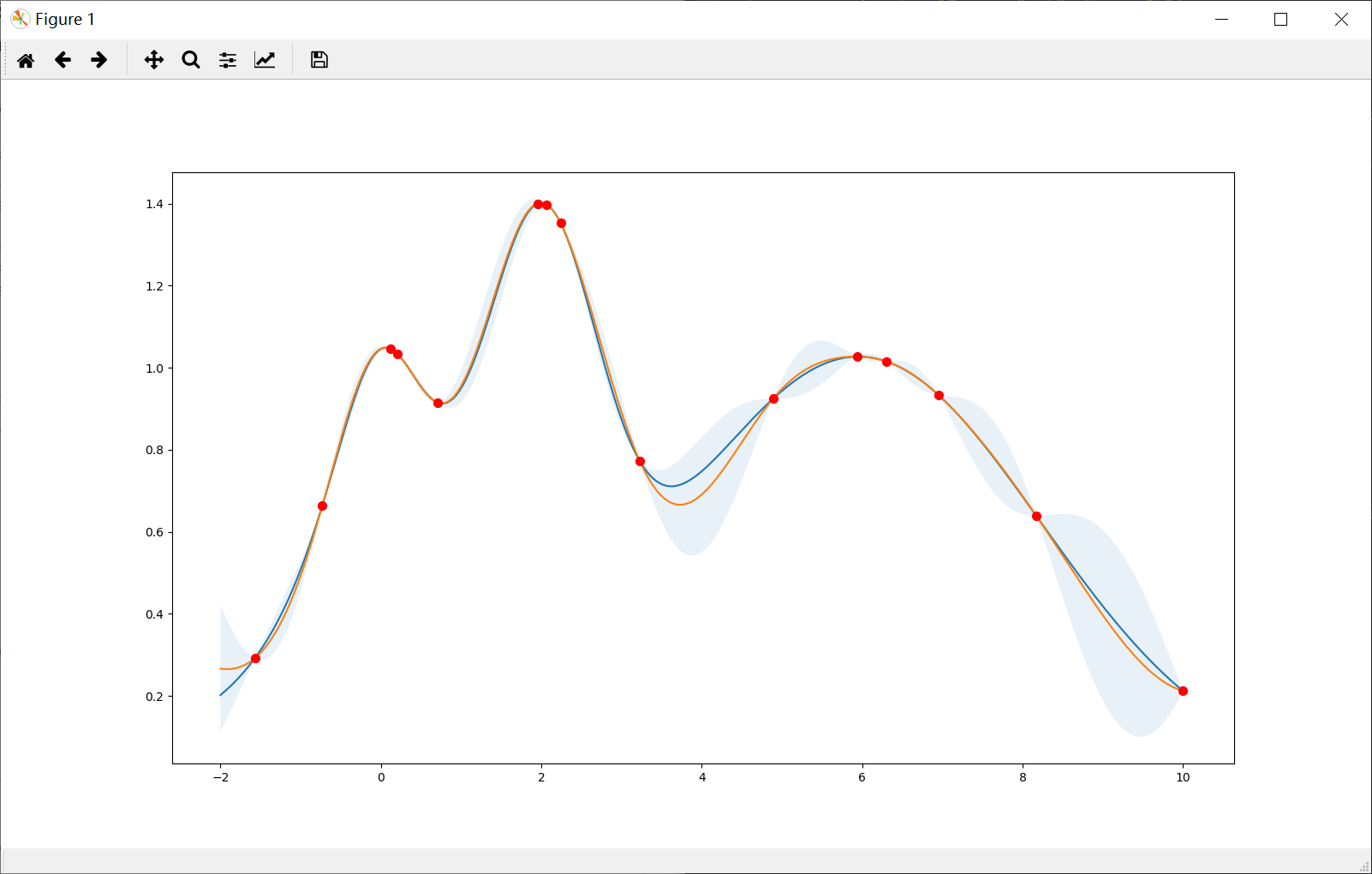
image
Prefer exploration (xi=1e-1)
Note that the points are more spread out across the whole range.

1
2
3
4
5
6
7
8
9
10
bo = BayesianOptimization(
    f=f,
    pbounds={"x": (-2, 10)},
    verbose=0,
    random_state=987234,
)

bo.maximize(n_iter=10, acq="ei", xi=1e-1)

plot_bo(f, bo)

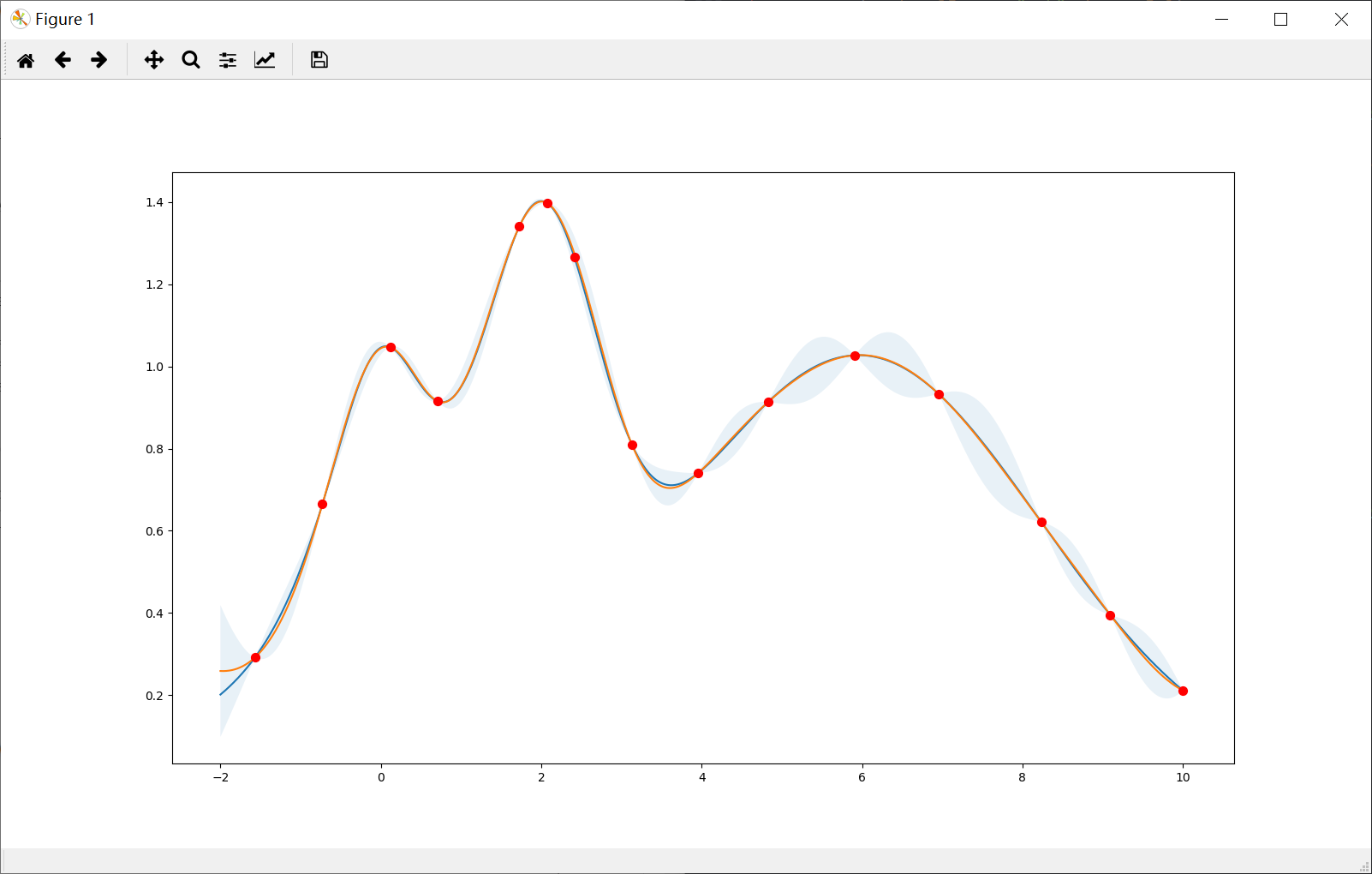
image

Probability of Improvement (POI)

Prefer exploitation (xi=1e-4)
Note that most points are around the peak(s).

1
2
3
4
5
6
7
8
9
10
bo = BayesianOptimization(
    f=f,
    pbounds={"x": (-2, 10)},
    verbose=0,
    random_state=987234,
)

bo.maximize(n_iter=10, acq="poi", xi=1e-4)

plot_bo(f, bo)

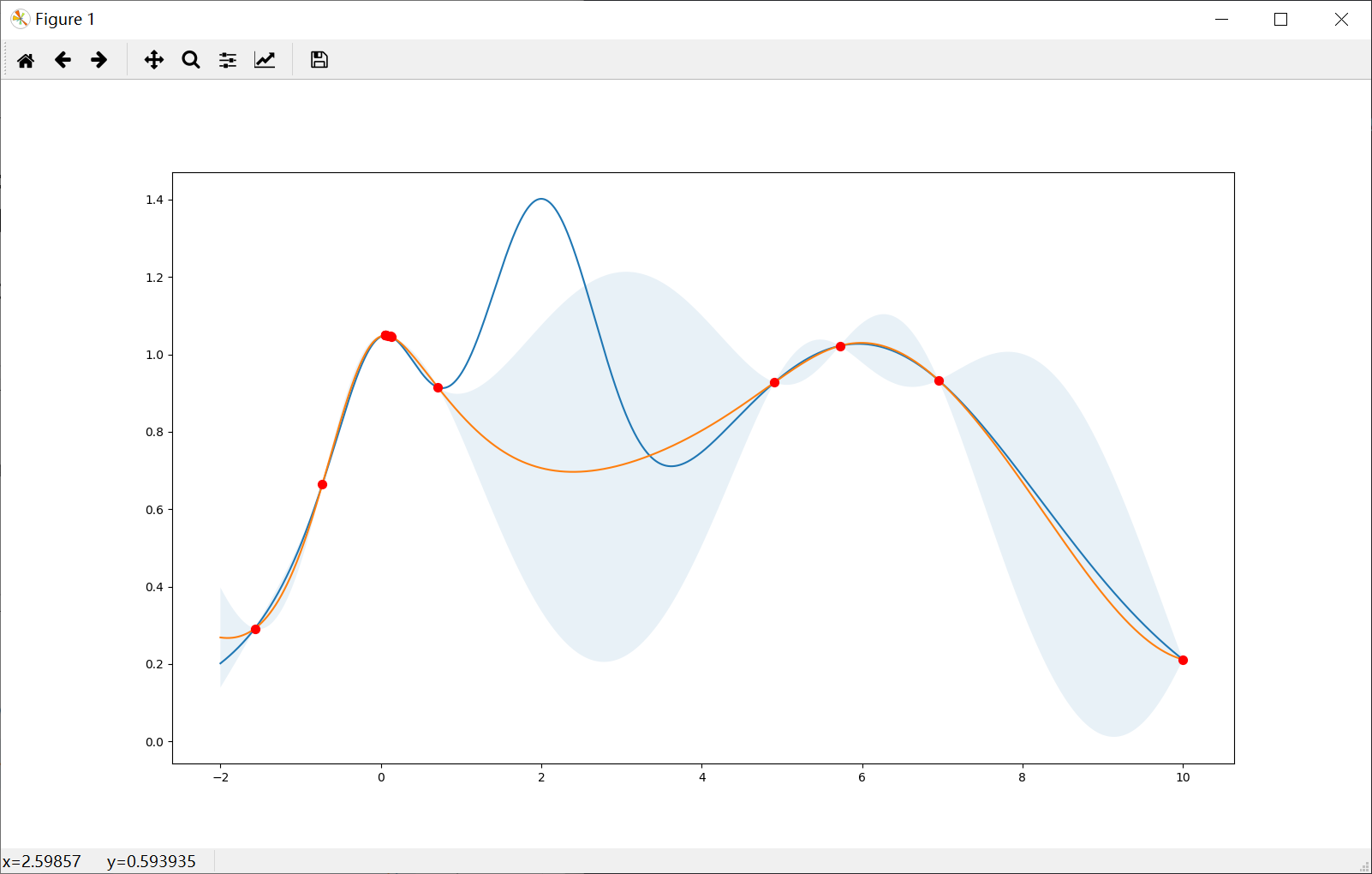
image
Prefer exploration (xi=1e-1)
Note that the points are more spread out across the whole range.

1
2
3
4
5
6
7
8
9
10
bo = BayesianOptimization(
    f=f,
    pbounds={"x": (-2, 10)},
    verbose=0,
    random_state=987234,
)

bo.maximize(n_iter=10, acq="poi", xi=1e-1)

plot_bo(f, bo)

image

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
import numpy as np
import matplotlib.pyplot as plt
from bayes_opt import BayesianOptimization

np.random.seed(42)
xs = np.linspace(-2, 10, 10000)


# Target function
def f(x):
    return np.exp(-(x - 2) ** 2) + np.exp(-(x - 6) ** 2 / 10) + 1 / (x ** 2 + 1)


plt.plot(xs, f(xs))
plt.show()


# Utility function for plotting
def plot_bo(f, bo):
    x = np.linspace(-2, 10, 10000)
    mean, sigma = bo._gp.predict(x.reshape(-1, 1), return_std=True)

    plt.figure(figsize=(16, 9))
    plt.plot(x, f(x))
    plt.plot(x, mean)
    plt.fill_between(x, mean+sigma, mean-sigma, alpha=0.1)
    plt.scatter(bo.space.params.flatten(), bo.space.target, c='red', s=50, zorder=10)
    plt.show()


# Acquisition Function 'Upper Confidence Bound'

# Prefer exploitation (kappa=0.1)
# Note that most points are around the peak(s).
bo = BayesianOptimization(
    f=f,
    pbounds={'x': (-2, 10)},
    verbose=0,
    random_state=987234
)

bo.maximize(n_iter=10, acq='ucb', kappa=0.1)
plot_bo(f, bo)

# Prefer exploration (kappa=10)
# Note that the points are more spread out across the whole range.
bo = BayesianOptimization(
    f=f,
    pbounds={'x':(-2, 10)},
    verbose=0,
    random_state=987234
)

bo.maximize(n_iter=10, acq='ucb', kappa=10)
plot_bo(f, bo)


# Acquisition Function 'Expected Improvement'

# Prefer exploitation (xi=0.0)
# Note that most points are around the peak(s).
bo = BayesianOptimization(
    f=f,
    pbounds={'x': (-2, 10)},
    verbose=0,
    random_state=987234
)

bo.maximize(n_iter=10, acq='ei', xi=1e-4)
plot_bo(f, bo)

# Prfer exploration (xi=0.1)
# Note that the points are more spread out across the whole range.
bo = BayesianOptimization(
    f=f,
    pbounds={'x': (-2, 10)},
    verbose=0,
    random_state=987234
)

bo.maximize(n_iter=10, acq='ei', xi=1e-1)
plot_bo(f, bo)


# Acquisition Function 'Probability of Improvement'
# Prefer exploitation (xi=0.0001)
# Note that most points are around the peak(s).
bo = BayesianOptimization(
    f=f,
    pbounds={'x': (-2, 10)},
    verbose=0,
    random_state=987234
)

bo.maximize(n_iter=10, acq='poi', xi=1e-4)
plot_bo(f, bo)

bo = BayesianOptimization(
    f=f,
    pbounds={'x': (-2, 10)},
    verbose=0,
    random_state=987234
)

bo.maximize(n_iter=10, acq='poi', xi=1e-1)
plot_bo(f, bo)

Sequential Domain Reduction

Background

Sequential domain reduction is a process where the bounds of the optimization problem are mutated (typically contracted) to reduce the time required to converge to an optimal value. The advantage of this method is typically seen when a cost function is particularly expensive to calculate, or if the optimization routine oscilates heavily.

Basics

The basic steps are a pan and a zoom. These two steps are applied at one time, therefore updating the problem search space evey iteration.
Pan: recentering the region of interest around the most optimal point found.
Zoom: contract the region of interest.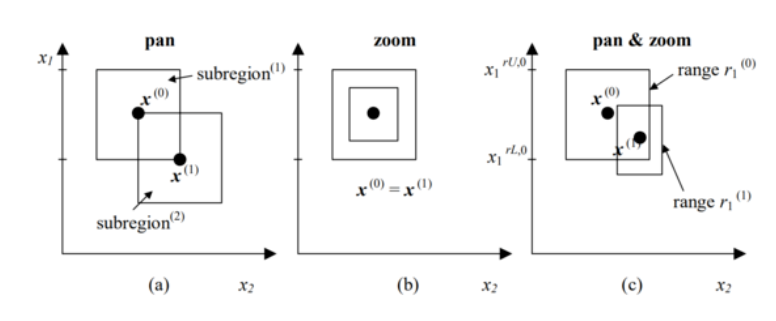
image

Parameters

There are three parameters for the built-in SequentialDomainReductionTransformer object:
$\gamma_{osc}:$ shrinkage parameter for oscillation. Typically [0.5-0.7]. Default = 0.7
$\gamma_{pan}:$ panning parameter. Typically 1.0. Default = 1.0
$\eta:$ zoom parameter. Default = 0.9

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
import numpy as np
import matplotlib.pyplot as plt
from bayes_opt import BayesianOptimization
from bayes_opt import SequentialDomainReductionTransformer


# cost function
def ackley(**kwargs):
    x = np.fromiter(kwargs.values(), dtype=float)
    arg1 = -0.2 * np.sqrt(0.5 * (x[0] ** 2 + x[1] ** 2))
    arg2 = 0.5 * (np.cos(2. * np.pi * x[0]) + np.cos(2. * np.pi * x[1]))
    return -1.0 * (-20. * np.exp(arg1) - np.exp(arg2) + 20. + np.e)


pbounds = {'x': (-5, 5), 'y': (-5, 5)}
bounds_transformer = SequentialDomainReductionTransformer()

mutating_optimizer = BayesianOptimization(
    f=ackley,
    pbounds=pbounds,
    verbose=0,
    random_state=10,
    bounds_transformer=bounds_transformer
)

mutating_optimizer.maximize(
    init_points=2,
    n_iter=50
)

standard_optimizer = BayesianOptimization(
    f=ackley,
    pbounds=pbounds,
    verbose=0,
    random_state=10
)

standard_optimizer.maximize(
    init_points=2,
    n_iter=50
)

print(mutating_optimizer.space.target)
print(standard_optimizer.space.target)
plt.plot(mutating_optimizer.space.target, label='Mutated Optimizer')
plt.plot(standard_optimizer.space.target, label='Standard Optimizer')
plt.legend()
plt.show()

# Plot the actual contraction of one of the variables(x)
x_min_bound = [b[0][0] for b in bounds_transformer.bounds]
x_max_bound = [b[0][1] for b in bounds_transformer.bounds]

x = [x[0] for x in mutating_optimizer.space.params]

plt.plot(x_min_bound[1:], label='x lower bound')
plt.plot(x_max_bound[1:], label='x upper bound')
plt.plot(x[1:], label='x')
plt.legend()
plt.show()

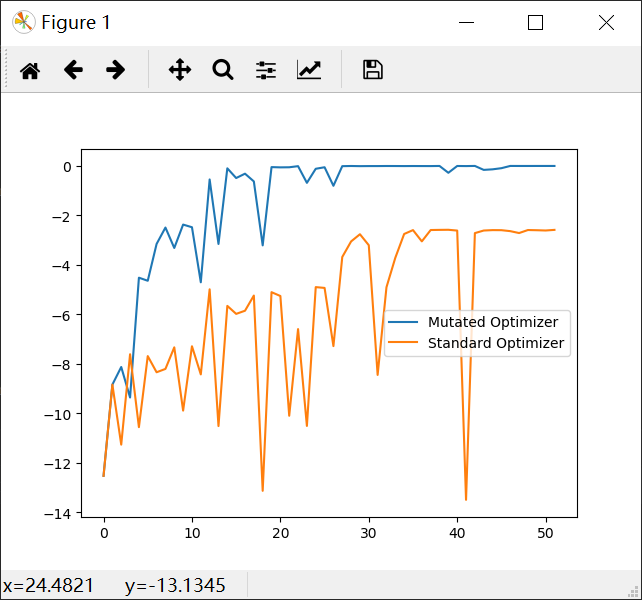
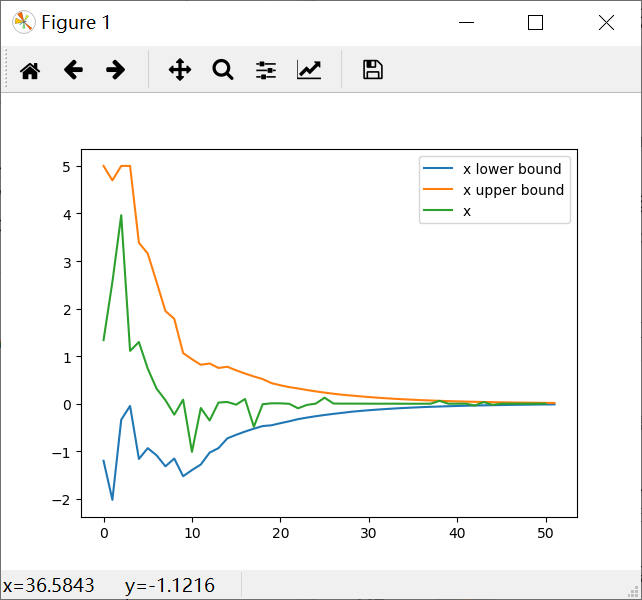
image
image

Ideas for distributed fshion

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
import time
import random

from bayes_opt import BayesianOptimization
from bayes_opt import UtilityFunction
from bayes_opt.util import Colours

import asyncio
import threading

try:
    import json
    import tornado
    import tornado.ioloop
    import tornado.httpserver
    from tornado.web import RequestHandler
    import requests
except ImportError:
    raise ImportError(
        "In order to run this example you must have the libraries: " +
        "'tornado' and 'requests' installed."
    )


def black_box_function(x, y):
    """
    Function with unknown internals we wish to maximize.

    This is just serving as an example, however, for all intents and
    purposes think of the internals of this function, i.e.: the process
    which generates its outputs values, as unkown.
    :param x:
    :param y:
    :return:
    """
    time.sleep(random.randint(1, 7))
    return -x ** 2 - (y - 1) ** 2 + 1


class BayesianOptimizationHandler(RequestHandler):
    """
    Basic functionality for NLP handlers.
    """
    _bo = BayesianOptimization(
        f=black_box_function,
        pbounds={'x': (-4, 4), 'y': (-3, 3)}
    )
    _uf = UtilityFunction(kind='ucb', kappa=3, xi=1)

    def post(self):
        """
        Deal with incoming requests.
        :return:
        """
        body = tornado.web.escape.json_decode(self.request.body)
        try:
            self._bo.register(
                params=body['params'],
                target=body['target']
            )
            print('BO has registered: {} points.'.format(len(self._bo.space)), end='\n\n')
        except KeyError:
            pass
        finally:
            suggested_params = self._bo.suggest(self._uf)

        self.write(json.dumps(suggested_params))


def run_optimization_app():
    asyncio.set_event_loop(asyncio.new_event_loop())
    handlers = [
        (r'/bayesian_optimization', BayesianOptimizationHandler)
    ]
    server = tornado.httpserver.HTTPServer(
        tornado.web.Application(handlers)
    )
    server.listen(9009)
    tornado.ioloop.IOLoop.instance().start()


def run_optimizer():
    global optimizers_config
    config = optimizers_config.pop()
    name = config['name']
    colour = config['colour']

    register_data = {}
    max_target = None
    for _ in range(10):
        status = name + ' wants to register: {}.\n'.format(register_data)

        resp = requests.post(
            url='http://localhost:9009/bayesian_optimization',
            json=register_data
        ).json()
        target = black_box_function(**resp)

        register_data = {
            'params': resp,
            'target': target
        }

        if max_target is None or target > max_target:
            max_target = target

        status += name + ' got {} as target.\n'.format(target)
        status += name + ' will to register next: {}.\n'.format(register_data)
        print(colour(status), end='\n')

    global results
    results.append((name, max_target))
    print(colour(name + ' is done!'), end='\n\n')


if __name__ == '__main__':
    ioloop = tornado.ioloop.IOLoop.instance()
    optimizers_config = [
        {'name': 'optimizer 1', 'colour': Colours.red},
        {'name': 'optimizer 2', 'colour': Colours.green},
        {'name': 'optimizer 3', 'colour': Colours.blue}
    ]

    app_thread = threading.Thread(target=run_optimization_app)
    app_thread.daemon = True
    app_thread.start()

    targets = (
        run_optimizer,
        run_optimizer,
        run_optimizer
    )
    optimizer_threads = []
    for target in targets:
        optimizer_threads.append(threading.Thread(target=target))
        optimizer_threads[-1].daemon = True
        optimizer_threads[-1].start()

    results = []
    for optimizer_thread in optimizer_threads:
        optimizer_thread.join()

    for result in results:
        print(result[0], 'found a maximum value of: {}'.format(result[1]))

    ioloop.stop()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
optimizer 2 wants to register: {}.
optimizer 2 got -10.104806757734842 as target.
optimizer 2 will to register next: {'params': {'x': -2.6685897265997385, 'y': -0.9958546111431001}, 'target': -10.104806757734842}.

BO has registered: 1 points.

optimizer 1 wants to register: {}.
optimizer 1 got -0.08624223735998338 as target.
optimizer 1 will to register next: {'params': {'x': -0.825933259800796, 'y': 1.6356701091877879}, 'target': -0.08624223735998338}.

optimizer 3 wants to register: {}.
optimizer 3 got -8.84605904099106 as target.
optimizer 3 will to register next: {'params': {'x': -2.4191200736626692, 'y': -0.998478698959131}, 'target': -8.84605904099106}.

BO has registered: 2 points.

BO has registered: 3 points.

optimizer 1 wants to register: {'params': {'x': -0.825933259800796, 'y': 1.6356701091877879}, 'target': -0.08624223735998338}.
optimizer 1 got -0.03271693601239223 as target.
optimizer 1 will to register next: {'params': {'x': -0.8217715406036188, 'y': 1.5978364919159311}, 'target': -0.03271693601239223}.

BO has registered: 4 points.

optimizer 3 wants to register: {'params': {'x': -2.4191200736626692, 'y': -0.998478698959131}, 'target': -8.84605904099106}.
optimizer 3 got -3.1541069118879657 as target.
optimizer 3 will to register next: {'params': {'x': -0.478848561163403, 'y': 2.9811135675068465}, 'target': -3.1541069118879657}.

BO has registered: 5 points.

optimizer 3 wants to register: {'params': {'x': -0.478848561163403, 'y': 2.9811135675068465}, 'target': -3.1541069118879657}.
optimizer 3 got 0.3506395031823706 as target.
optimizer 3 will to register next: {'params': {'x': -0.5535296916260822, 'y': 1.5856324592318665}, 'target': 0.3506395031823706}.

BO has registered: 6 points.

optimizer 2 wants to register: {'params': {'x': -2.6685897265997385, 'y': -0.9958546111431001}, 'target': -10.104806757734842}.
optimizer 2 got -18.410660902242956 as target.
optimizer 2 will to register next: {'params': {'x': 3.9747090775727596, 'y': 2.9006179655321738}, 'target': -18.410660902242956}.

BO has registered: 7 points.

optimizer 3 wants to register: {'params': {'x': -0.5535296916260822, 'y': 1.5856324592318665}, 'target': 0.3506395031823706}.
optimizer 3 got 0.7176990191956286 as target.
optimizer 3 will to register next: {'params': {'x': -0.4667130278578412, 'y': 1.25392898698679}, 'target': 0.7176990191956286}.

BO has registered: 8 points.

optimizer 1 wants to register: {'params': {'x': -0.8217715406036188, 'y': 1.5978364919159311}, 'target': -0.03271693601239223}.
optimizer 1 got 0.2937149514782076 as target.
optimizer 1 will to register next: {'params': {'x': -0.5954803587328559, 'y': 1.5930330436705713}, 'target': 0.2937149514782076}.

BO has registered: 9 points.

optimizer 2 wants to register: {'params': {'x': 3.9747090775727596, 'y': 2.9006179655321738}, 'target': -18.410660902242956}.
optimizer 2 got 0.6188257608900638 as target.
optimizer 2 will to register next: {'params': {'x': -0.520647571942313, 'y': 1.3318137202415088}, 'target': 0.6188257608900638}.

BO has registered: 10 points.

optimizer 1 wants to register: {'params': {'x': -0.5954803587328559, 'y': 1.5930330436705713}, 'target': 0.2937149514782076}.
optimizer 1 got 0.9220134755091871 as target.
optimizer 1 will to register next: {'params': {'x': -0.09305618205849499, 'y': 1.2633003446095525}, 'target': 0.9220134755091871}.

BO has registered: 11 points.

optimizer 3 wants to register: {'params': {'x': -0.4667130278578412, 'y': 1.25392898698679}, 'target': 0.7176990191956286}.
optimizer 3 got 0.8729321406148731 as target.
optimizer 3 will to register next: {'params': {'x': -0.16919630494098584, 'y': 1.3137522426683892}, 'target': 0.8729321406148731}.

BO has registered: 12 points.

optimizer 1 wants to register: {'params': {'x': -0.09305618205849499, 'y': 1.2633003446095525}, 'target': 0.9220134755091871}.
optimizer 1 got 0.962844200127132 as target.
optimizer 1 will to register next: {'params': {'x': -0.016057367058444766, 'y': 0.8079115806821808}, 'target': 0.962844200127132}.

BO has registered: 13 points.

optimizer 2 wants to register: {'params': {'x': -0.520647571942313, 'y': 1.3318137202415088}, 'target': 0.6188257608900638}.
optimizer 2 got 0.9475011601739508 as target.
optimizer 2 will to register next: {'params': {'x': 0.008136377622403344, 'y': 1.228981744218256}, 'target': 0.9475011601739508}.

BO has registered: 14 points.

optimizer 1 wants to register: {'params': {'x': -0.016057367058444766, 'y': 0.8079115806821808}, 'target': 0.962844200127132}.
optimizer 1 got 0.681607524343745 as target.
optimizer 1 will to register next: {'params': {'x': 0.5470530915007933, 'y': 0.861705420439991}, 'target': 0.681607524343745}.

BO has registered: 15 points.

optimizer 2 wants to register: {'params': {'x': 0.008136377622403344, 'y': 1.228981744218256}, 'target': 0.9475011601739508}.
optimizer 2 got 0.48596533634302996 as target.
optimizer 2 will to register next: {'params': {'x': 0.6494555952970329, 'y': 0.6962861652898461}, 'target': 0.48596533634302996}.

BO has registered: 16 points.

optimizer 3 wants to register: {'params': {'x': -0.16919630494098584, 'y': 1.3137522426683892}, 'target': 0.8729321406148731}.
optimizer 3 got 0.8935410088779421 as target.
optimizer 3 will to register next: {'params': {'x': 0.019473583880974782, 'y': 0.6743011043112234}, 'target': 0.8935410088779421}.

BO has registered: 17 points.

optimizer 1 wants to register: {'params': {'x': 0.5470530915007933, 'y': 0.861705420439991}, 'target': 0.681607524343745}.
optimizer 1 got 0.014030446537434904 as target.
optimizer 1 will to register next: {'params': {'x': 0.3545856212730503, 'y': 0.07250951991464082}, 'target': 0.014030446537434904}.

BO has registered: 18 points.

optimizer 2 wants to register: {'params': {'x': 0.6494555952970329, 'y': 0.6962861652898461}, 'target': 0.48596533634302996}.
optimizer 2 got -0.024930628032141522 as target.
optimizer 2 will to register next: {'params': {'x': 0.008487168509559948, 'y': -0.01235299970061423}, 'target': -0.024930628032141522}.

BO has registered: 19 points.

optimizer 3 wants to register: {'params': {'x': 0.019473583880974782, 'y': 0.6743011043112234}, 'target': 0.8935410088779421}.
optimizer 3 got -1.1593358417915587 as target.
optimizer 3 will to register next: {'params': {'x': 0.304036722051486, 'y': -0.4376708640838995}, 'target': -1.1593358417915587}.

BO has registered: 20 points.

optimizer 1 wants to register: {'params': {'x': 0.3545856212730503, 'y': 0.07250951991464082}, 'target': 0.014030446537434904}.
optimizer 1 got 0.3621855314818603 as target.
optimizer 1 will to register next: {'params': {'x': -0.5211480943816511, 'y': 0.394839581399681}, 'target': 0.3621855314818603}.

BO has registered: 21 points.

optimizer 1 wants to register: {'params': {'x': -0.5211480943816511, 'y': 0.394839581399681}, 'target': 0.3621855314818603}.
optimizer 1 got -31.0 as target.
optimizer 1 will to register next: {'params': {'x': 4.0, 'y': -3.0}, 'target': -31.0}.

BO has registered: 22 points.

optimizer 2 wants to register: {'params': {'x': 0.008487168509559948, 'y': -0.01235299970061423}, 'target': -0.024930628032141522}.
optimizer 2 got 0.2212009910225048 as target.
optimizer 2 will to register next: {'params': {'x': 0.6663278244883658, 'y': 1.578624437169825}, 'target': 0.2212009910225048}.

BO has registered: 23 points.

optimizer 3 wants to register: {'params': {'x': 0.304036722051486, 'y': -0.4376708640838995}, 'target': -1.1593358417915587}.
optimizer 3 got 0.1608408642161967 as target.
optimizer 3 will to register next: {'params': {'x': 0.6849146248958657, 'y': 1.6083182492639514}, 'target': 0.1608408642161967}.

BO has registered: 24 points.

optimizer 1 wants to register: {'params': {'x': 4.0, 'y': -3.0}, 'target': -31.0}.
optimizer 1 got 0.9650142542083455 as target.
optimizer 1 will to register next: {'params': {'x': 0.17771902492240965, 'y': 0.941675957167885}, 'target': 0.9650142542083455}.

optimizer 1 is done!

optimizer 3 wants to register: {'params': {'x': 0.6849146248958657, 'y': 1.6083182492639514}, 'target': 0.1608408642161967}.
optimizer 3 got 0.9735847112744838 as target.
optimizer 3 will to register next: {'params': {'x': 0.1554569849815957, 'y': 0.9525825501956485}, 'target': 0.9735847112744838}.

BO has registered: 25 points.

optimizer 2 wants to register: {'params': {'x': 0.6663278244883658, 'y': 1.578624437169825}, 'target': 0.2212009910225048}.
optimizer 2 got 0.9004308681733019 as target.
optimizer 2 will to register next: {'params': {'x': -0.2564624958036852, 'y': 0.8161627892051153}, 'target': 0.9004308681733019}.

BO has registered: 26 points.

optimizer 3 wants to register: {'params': {'x': 0.1554569849815957, 'y': 0.9525825501956485}, 'target': 0.9735847112744838}.
optimizer 3 got 0.9913624079492526 as target.
optimizer 3 will to register next: {'params': {'x': -0.09037572810596849, 'y': 1.0216753274499712}, 'target': 0.9913624079492526}.

optimizer 3 is done!

optimizer 2 wants to register: {'params': {'x': -0.2564624958036852, 'y': 0.8161627892051153}, 'target': 0.9004308681733019}.
optimizer 2 got 0.9954765125703233 as target.
optimizer 2 will to register next: {'params': {'x': -0.060520522856410255, 'y': 1.0293386049917745}, 'target': 0.9954765125703233}.

BO has registered: 27 points.

optimizer 2 wants to register: {'params': {'x': -0.060520522856410255, 'y': 1.0293386049917745}, 'target': 0.9954765125703233}.
optimizer 2 got 0.9973831688359093 as target.
optimizer 2 will to register next: {'params': {'x': 0.04239868741169467, 'y': 1.0286213638713488}, 'target': 0.9973831688359093}.

optimizer 2 is done!

optimizer 1 found a maximum value of: 0.9650142542083455
optimizer 3 found a maximum value of: 0.9913624079492526
optimizer 2 found a maximum value of: 0.9973831688359093

Process finished with exit code 0

Deep Learning Example

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
from mxnet import autograd, gluon, init, nd
from mxnet.gluon import nn, data as gdata, loss as gloss
import mxnet as mx
import sys
import os
import time
from bayes_opt import BayesianOptimization

os.environ['CUDA_VISIBLE_DEVICES'] = '6'


def try_gpu():
    try:
        ctx = mx.cpu()
        _ = nd.array((1,), ctx=ctx)
    except mx.base.MXNetError:
        ctx = mx.cpu()
    return ctx


def load_data_fashion_mnist(batch_size, resize=None, root=os.path.join('mxnet', 'datasets', 'fashion-mnist')):
    root = os.path.expanduser(root)
    transformer = []
    if resize:
        transformer += [gdata.vision.transforms.Resize(resize)]
    transformer += [gdata.vision.transforms.ToTensor()]
    transformer = gdata.vision.transforms.Compose(transformer)

    mnist_train = gdata.vision.FashionMNIST(root=root, train=True)
    mnist_test = gdata.vision.FashionMNIST(root=root, train=False)

    num_workers = 0 if sys.platform.startswith('win') else 4
    train_iter = gdata.DataLoader(mnist_train.transform_first(transformer),
                                  batch_size=batch_size,
                                  shuffle=True,
                                  num_workers=num_workers)
    test_iter = gdata.DataLoader(mnist_test.transform_first(transformer),
                                 batch_size=batch_size,
                                 shuffle=True,
                                 num_workers=num_workers)
    return train_iter, test_iter


def evaluate_accuracy(net, data_iter, ctx):
    acc_sum, n = nd.array([0], ctx=ctx), 0
    for X, y in data_iter:
        X, y = X.as_in_context(ctx), y.as_in_context(ctx).astype('float32')
        y_hat = net(X)
        acc_sum += (y_hat.argmax(axis=1) == y).sum()
        n += y.size
    return acc_sum.asscalar() / n


def train(net, train_iter, test_iter, batch_size, trainer, ctx, num_epochs):
    print("training on ", ctx)
    loss = gloss.SoftmaxCrossEntropyLoss()
    test_acc = 0.0
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n, start = 0.0, 0.0, 0, time.time()
        for X, y in train_iter:
            X, y = X.as_in_context(ctx), y.as_in_context(ctx)
            with autograd.record():
                y_hat = net(X)
                l = loss(y_hat, y).sum()
            l.backward()
            trainer.step(batch_size)
            train_l_sum += l.asscalar()
            train_acc_sum += (y_hat.argmax(axis=1) == y.astype('float32')).sum().asscalar()
            n += y.size
        test_acc = evaluate_accuracy(net, test_iter, ctx)
        print('epoch %3d, loss %.4f, train acc %.3f, test acc %.3f, time %.1f sec'
              % (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc, time.time() - start))
    return test_acc


# 定义模型
net = nn.Sequential()
net.add(
    # LeNet包含卷积层块和全连接层块
    # 卷积层块：
    # 卷积层块包含两个基本单位：每个基本单位包含一个卷积层和一个最大池化层
    # 第一个卷积层输出通道数为6，第二个为16
    # 池化层窗口大小2×2，步幅均为2
    nn.Conv2D(channels=6, kernel_size=5, activation='sigmoid'),
    nn.MaxPool2D(pool_size=2, strides=2),
    nn.Conv2D(channels=16, kernel_size=5, activation='sigmoid'),
    nn.MaxPool2D(pool_size=2, strides=2),
    # 全连接层块：
    # 全连接层块包含三个全连接层
    # 输出分别是120，84,10(此10为类别个数)
    # 卷积层输出形状为(batch_size, channels, height, width)，
    # 全连接层输入将卷积层输出flatten为形状(batch_size, channels*height*width)
    nn.Dense(120, activation='sigmoid'),
    nn.Dense(84, activation='sigmoid'),
    nn.Dense(10)
)

lr, num_epochs, batch_size, ctx = 0.1, 1, 64, try_gpu()
net.initialize(force_reinit=True, ctx=ctx, init=init.Xavier())
# trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': lr})
# train_iter, test_iter = load_data_fashion_mnist(batch_size, resize=12)
# train(net, train_iter, test_iter, batch_size, trainer, ctx, num_epochs)


def cost_function(batch_size, lr):
    batch_size = int(batch_size)
    trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': lr})
    train_iter, test_iter = load_data_fashion_mnist(batch_size, resize=28)
    return train(net, train_iter, test_iter, batch_size, trainer, ctx, num_epochs)


bayesian_optimizer = BayesianOptimization(
    f=cost_function,
    pbounds={'batch_size': (1, 16), 'lr': (1e-4, 1)}
)

bayesian_optimizer.maximize(init_points=2, n_iter=2)
print(bayesian_optimizer.max)

Reference

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

做一个安静细微的人，<br> 于角落里自在开放，<br> 默默悦人，<br> 却始终不引起过分热闹的关注，<br> 保有独立而随意的品格，<br> 这就很好。<br><br> Stick to what you insist on,<br> believe what you believe!<br> Life hastily for decades,<br> do what I can!